حلول ومنتديات لألبوم الحلول - الديناميكا في خط مستقيم

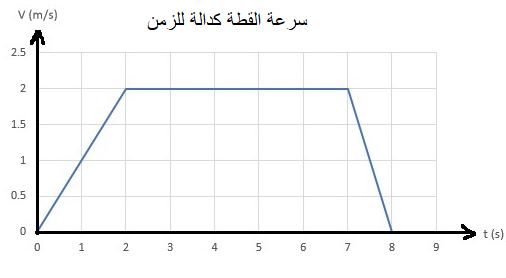
تتحرك القطة من النقطة  A إلى النقطة B. وتم وصف حركتها في رسم بياني للسرعة كدالة للزمن.

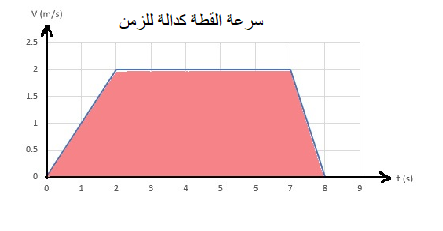
في الرسم البياني للسرعة كدالة للزمن ، فإن المساحة المحصورة بين الرسم البياني والمحور الزمني مساوية للإزاحة ، لذلك لحساب البعد بين النقطة A والنقطة B ، نحسب المساحة المحصورة بين الرسم البياني والمحور الزمني :

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»*«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»13«/mn»«mi mathvariant=¨bold¨»m«/mi»«/msub»«/math»

1. يمكنك حساب المساحة المحصورة باستخدام صيغة مساحة شبه المنحرف:

                                                  «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#FF0000¨»S«/mi»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1575;§#1604;§#1605;§#1606;§#1581;§#1585;§#1601;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1588;§#1576;§#1607;«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1602;§#1575;§#1593;§#1583;§#1578;§#1610;§#1606;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1605;§#1580;§#1605;§#1608;§#1593;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»*«/mo»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1573;§#1585;§#1578;§#1601;§#1575;§#1593;«/mi»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«/math»

  يمكن تقسيم شبه المنحرف إلى ثلاثة أجزاء: مثلثين ومستطيل ، مساحة شبه المنحرف تساوي مجموع المساحات الثلاث.

2. البعد مساوٍ لإزاحة الحركة ، لكنه لا يمكن أن يكون سالب. البعد هو القيمة المطلقة للإزاحة. 

تتسبب قوة الاحتكاك في تحرك الدمية بسرعة آخذة بالنقصان، وتتحرك الدمية بتسارع ثابت وسالب.

نشير إلى حركة الدمية من اللحظة التي بدأت فيها التحرك من النقطة B حتى وصلت إلى النقطة A.

البعد بين النقطة B والنقطة A هي 13 مترًا - وبالتالي فإن إزاحة حركتها هي 13 مترًا.

زمن حركة الدمية أقل من زمن حركة القطة بمقدار ثانية ونصف - وبالتالي فإن زمن حركة الدمية هو 6.5 ثانية. 

تتحرك الدمية حتى تصل إلى النقطة B - وبالتالي فإن سرعة الدمية في النقطة B تساوي صفرًا. 

نستخدم دالة المكان كدالة للزمن، المناسبة للحركة بتسارع ثابت: 

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»v«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»v«/mi»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«/math»

نعبّر عن السرعة الابتدائية من هذه الدالة:

                                                                             «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mspace linebreak=¨newline¨»«/mspace»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfenced mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mspace linebreak=¨newline¨»«/mspace»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«mi mathvariant=¨bold¨»t«/mi»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»

نعوّض المعطيات في التعبير الذي طورناه، ونجد السرعة الابتدائية: 

تعمل ثلاث قوى على الدمية: قوة الجاذبية نحو الأسفل، القوة العمودية نحو الأعلى. وقوة الاحتكاك الحركي في الاتجاه المعاكس للحركة.

نرسم مخطط قوة:

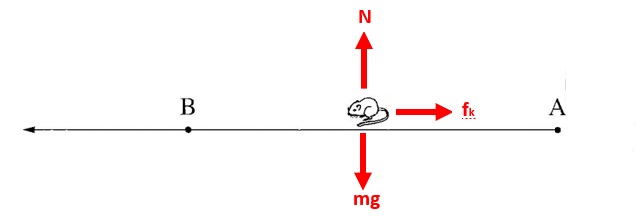
لإيجاد معامل الاحتكاك ، نكتب معادلات الحركة:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨»y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»          «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mtable mathcolor=¨#0000FF¨ columnalign=¨right¨»«mtr»«mtd»«mi mathvariant=¨bold¨»§#931;«/mi»«msub»«mi mathvariant=¨bold¨»F«/mi»«mi mathvariant=¨bold¨»x«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»ma«/mi»«/mtd»«/mtr»«mtr»«mtd»«menclose notation=¨box¨»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»ma«/mi»«/menclose»«/mtd»«/mtr»«/mtable»«/math»

تتعلق قوة الاحتكاك الحركي بمعامل الاحتكاك الحركي والقوة العمودية وفقًا لـ  :          «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/mstyle»«/math»

نعبّر عن معامل الاحتكاك الحركي من تعريف قوة الاحتكاك الحركي ومعادلات الحركة:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»N«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»a«/mi»«/mrow»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«/menclose»«/mstyle»«/math»

لإيجاد معامل الاحتكاك ، نحسب تسارع الدمية:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»v«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»v«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»v«/mi»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»v«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»t«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»8«/mn»«mn mathvariant=¨bold¨»13«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»615«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»

لإيجاد معامل الاحتكاك نعوّض تسارع الدمية في التعبير عن معامل الاحتكاك: 

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mstyle mathvariant=¨bold¨ displaystyle=¨true¨»«mn»0«/mn»«mo».«/mo»«mn»615«/mn»«/mstyle»«/mrow»«mn mathvariant=¨bold¨»10«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0615«/mn»«/math»

בציר Y ישנו שקול כוחות ומכאן ש:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«munder mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»§#8721;«/mo»«mrow»«/mrow»«/munder»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨»y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»{«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»}«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»g«/mi»«/math»

בציר X נקבל ש:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfenced mathcolor=¨#0000FF¨ open=¨¨ close=¨}¨»«mtable columnalign=¨right¨»«mtr»«mtd»«mfenced open=¨¨ close=¨}¨»«mtable columnalign=¨right¨»«mtr»«mtd»«munder»«mo mathvariant=¨bold¨»§#8721;«/mo»«mrow»«/mrow»«/munder»«msub»«mi mathvariant=¨bold¨»F«/mi»«mi mathvariant=¨bold¨»x«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»a«/mi»«/mtd»«/mtr»«mtr»«mtd»«msub»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»N«/mi»«/mtd»«/mtr»«/mtable»«/mfenced»«mo mathvariant=¨bold¨»§#8658;«/mo»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»a«/mi»«/mtd»«/mtr»«mtr»«mtd»«mo mathvariant=¨bold¨»{«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»}«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mtd»«/mtr»«/mtable»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»{«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»}«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»

נמצא את תאוצת הצעצוע בעזרת משוואת התנועה עבור תנועה שוות-תאוצה:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»v«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»v«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»{«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»}«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»v«/mi»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»v«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»t«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»8«/mn»«mn mathvariant=¨bold¨»13«/mn»«/mfrac»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/msub»«/math»

נציב את {3} ב-{2} ונקבל ש:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mstyle displaystyle=¨true¨ mathvariant=¨bold¨»«mfrac»«mn»8«/mn»«mn»13«/mn»«/mfrac»«/mstyle»«/mrow»«mn mathvariant=¨bold¨»10«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»4«/mn»«mn mathvariant=¨bold¨»65«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0615«/mn»«/math»

בציר Y ישנו שקול כוחות ומכאן ש:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«munder mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»§#8721;«/mo»«mrow»«/mrow»«/munder»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨»y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»{«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»}«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»g«/mi»«/math»

בציר X נקבל ש:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfenced mathcolor=¨#0000FF¨ open=¨¨ close=¨}¨»«mtable columnalign=¨right¨»«mtr»«mtd»«mfenced open=¨¨ close=¨}¨»«mtable columnalign=¨right¨»«mtr»«mtd»«munder»«mo mathvariant=¨bold¨»§#8721;«/mo»«mrow»«/mrow»«/munder»«msub»«mi mathvariant=¨bold¨»F«/mi»«mi mathvariant=¨bold¨»x«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»a«/mi»«/mtd»«/mtr»«mtr»«mtd»«msub»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»N«/mi»«/mtd»«/mtr»«/mtable»«/mfenced»«mo mathvariant=¨bold¨»§#8658;«/mo»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»a«/mi»«/mtd»«/mtr»«mtr»«mtd»«mo mathvariant=¨bold¨»{«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»}«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mtd»«/mtr»«/mtable»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»{«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»}«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»

נמצא את תאוצת הצעצוע בעזרת משוואת התנועה עבור תנועה שוות-תאוצה:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»v«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»v«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»{«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»}«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»v«/mi»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»v«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»t«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»8«/mn»«mn mathvariant=¨bold¨»13«/mn»«/mfrac»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/msub»«/math»

נציב את {3} ב-{2} ונקבל ש:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mstyle displaystyle=¨true¨ mathvariant=¨bold¨»«mfrac»«mn»8«/mn»«mn»13«/mn»«/mfrac»«/mstyle»«/mrow»«mn mathvariant=¨bold¨»10«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»4«/mn»«mn mathvariant=¨bold¨»65«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0615«/mn»«/math»

1. التسارع - سيتغير ، يزداد معامل الاحتكاك وبالتالي تزداد قوة الاحتكاك ومن القانون الثاني لنيوتن سوف يزداد التسارع أيضًا.

2. زمن التوقف - يختلف ، تزداد القيمة المطلقة للتسارع، تزداد وتيرة تغيير السرعة،  سيكون زمن التوقف عن الحركة أصغر.

3. مسافة التوقف - تختلف ،  تزداد القيمة المطلقة للتسارع. زمن الحركة حتى التوقف أقصر ، وبالتالي فإن المسافة حتى التوقف ستكون أقصر أيضًا.

4. متوسط ​​السرعة - لن يتغير ، معطى متوسط ​​السرعة وفقًا لمتوسط ​​حسابي بسيط:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»v«/mi»«mi mathvariant=¨bold¨»§#1502;§#1502;§#1493;§#1510;§#1506;«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»v«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»v«/mi»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«/math»

 في كلتا الحالتين ، تكون السرعات الابتدائية والنهائية هي نفسها، وبالتالي فإن متوسط ​​السرعة هو نفسه أيضًا. 

باختصار: فقط متوسط ​​السرعة (الخيار 4) لا يتغير.