5. 2017,2 - منظومة مكوّنة من جسمين أحدهما على سطح أفقي

 ________________________________________________________________________________
________________________________________________________________________________

______________________________________________________________________________________

______________________________________________________________________________________
الدالة في الرسم البياني تكون تصاعدية حتى يصبح وزن السلة 4 نيوتن ، وتزداد قوة الاحتكاك وفقًا لذلك، وهي تساوي وزن السلة. حتى يصبح وزن السلة 4 نيوتن.
لأي وزن أكبر من 4 نيوتن ، تكون قوة الاحتكاك ثابتة ومقدارها 2.5 نيوتن.
لذلك من الرسم البياني يمكنك أن تفهم أن الحد الأقصى لقوة الاحتكاك الساكن هو 4 نيوتن ، مع وزن أكبر من 4 نيوتن تتحرك السلة. وكانت قوة الاحتكاك الحركي 2.5 نيوتن.
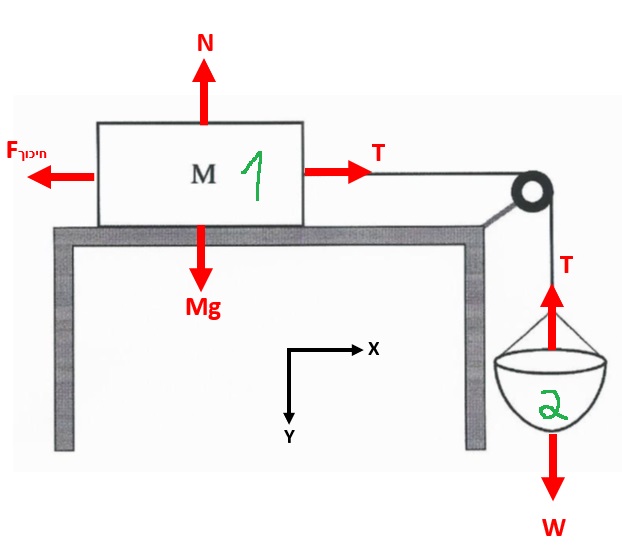
لحساب معامل الاحتكاك الساكن، نتطرّق إلى حالة حافة الحركة. نرسم مخطط القوى ونكتب معادلات الحركة:
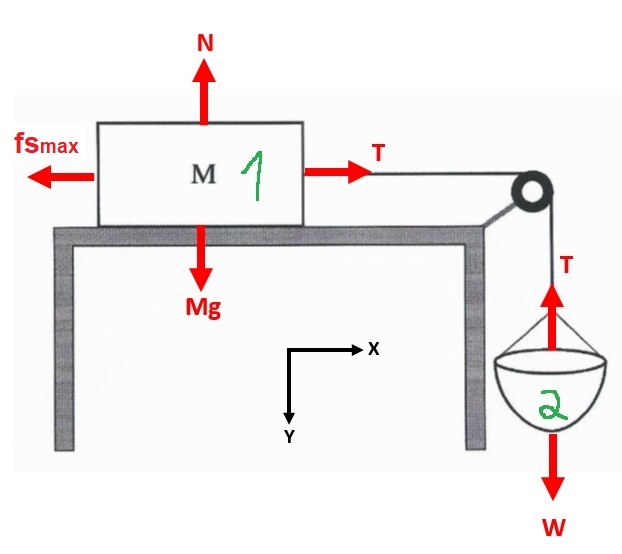
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow»«mi mathvariant=¨bold¨»Y«/mi»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«/math»«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow»«mi mathvariant=¨bold¨»X«/mi»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»f«/mi»«msub»«mi mathvariant=¨bold¨»s«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow»«mi mathvariant=¨bold¨»Y«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/math»
تتعلق قوة الاحتكاك الساكن على معامل الاحتكاك الساكن والقوة العمودية وفقًا لـ : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«msub»«mi mathvariant=¨bold¨»s«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/math»
نكتب تعبيرًا لمعامل الاحتكاك الساكن باستخدام معادلة الحركة العمودية للصندوق وتعريف قوة الاحتكاك الساكن:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»f«/mi»«msub»«mi mathvariant=¨bold¨»s«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«/msub»«mi mathvariant=¨bold¨»N«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»f«/mi»«msub»«mi mathvariant=¨bold¨»s«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«/msub»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»4«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»4«/mn»«mn mathvariant=¨bold¨»8«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«/math»
لذلك ، فإن مقدار معامل الاحتكاك الساكن هو 0.5 .
لحساب معامل الاحتكاك الحركي ، نتطرّق إلى حالة الحركة، عندما يكون وزن السلة أكبر من 4 نيوتن.
نرسم مخطط القوة ونكتب معادلات الحركة عندما يتحرك الصندوق:
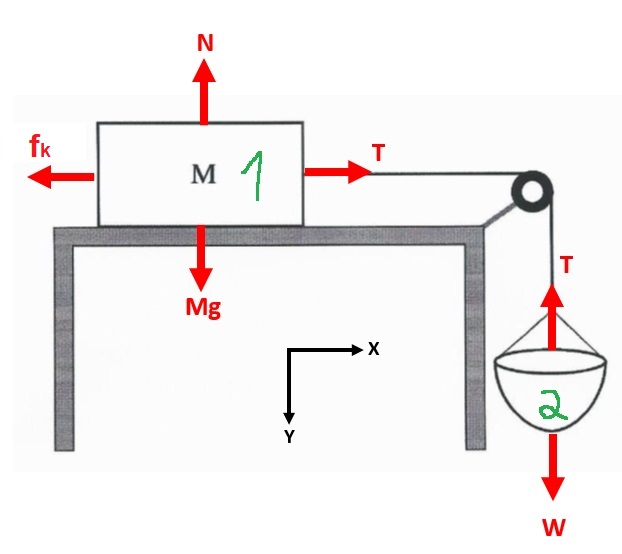
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow»«mi mathvariant=¨bold¨»Y«/mi»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«/math»«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow»«mi mathvariant=¨bold¨»X«/mi»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold-italic¨»k«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow»«mi mathvariant=¨bold¨»Y«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/math»
تتعلق قوة الاحتكاك الحركي على معامل الاحتكاك الحركي والقوة العمودية وفقًا لـ : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/math»
نكتب تعبيرًا لمعامل الاحتكاك الحركي باستخدام معادلة الحركة العمودية للصندوق وتعريف قوة الاحتكاك الحركي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»N«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»fk«/mi»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«mn mathvariant=¨bold¨»8«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3125«/mn»«/math»
لذلك ، فإن مقدار معامل الاحتكاك الساكن هو 0.3125 .
______________________________________________________________________________________
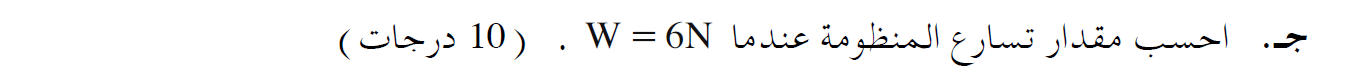
______________________________________________________________________________________
عندما يكون وزن السلة 6 نيوتن ، ينزلق الصندوق على الطاولة، وتؤثر عليه قوة الاحتكاك الحركية.
نرسم مخطط قوى ونكتب معادلات الحركة لهذه الحالة :
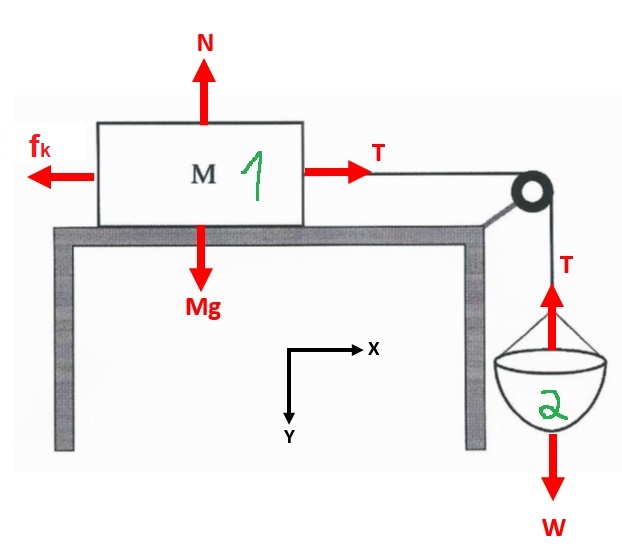
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow»«mi mathvariant=¨bold¨»X«/mi»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»fk«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»§#956;k«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»a«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/menclose»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«/math»«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow»«mi mathvariant=¨bold¨»Y«/mi»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow»«mi mathvariant=¨bold¨»Y«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»a«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«/menclose»«/math»
عندما ينزل الجسم 2 مسافة معينة، يتحرك الجسم 1 إلى اليمين بنفس المسافة تمامًا ، وتكون سرعة الجسمين متساوية في كل لحظة، وتتغير بنفس الوتيرة، وبالتالي فإن تسارعهما متساوٍ.
نشير إلى تسارع كل جسم بواسطة بواسطة a:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«/math»
نعبر عن تسارع الجسمين من معادلات الحركة ، ونعوّض قوة التوتر من معادلة حركة الجسم 2 في معادلة الحركة الأفقية للجسم 1.
نعوّض اقوة العمودية من معادلة الحركة الرأسية للجسم 1 في معادلة الحركة الأفقية للجسم 1:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»T«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»§#956;k«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#007F00¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;k«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#007F00¨»«mi mathvariant=¨bold¨ mathcolor=¨#007F00¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#007F00¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#007F00¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«/math»«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨ mathcolor=¨#007F00¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#007F00¨»=«/mo»«msub mathcolor=¨#007F00¨»«mi mathvariant=¨bold¨ mathcolor=¨#007F00¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#007F00¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#007F00¨»g«/mi»«/menclose»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#8659;«/mo»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»a«/mi»«/math»
نعبّر عن التسارع :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;k«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;k«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;k«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»§#956;k«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»
نعوّض المعطيات في تعبير التسارع ، ونحسب تسارع الأجسام:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»§#956;k«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3125«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
لذلك فإن تسارع المجموعة تساوي 2.5 متر لكل ثانية مربعة.

______________________________________________________________________________________
التعبير عن قوة الشد التي تم الحصول عليها من معادلة حركة السلة عندما تتحرك المنظومة بتسارع هو:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨»g«/mi»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«/menclose»«/math»
والتعبير عن قوة الشد عندما تكون المنظومة ساكنة بسبب الاحتكاك الساكن هو:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«/menclose»«/math»
______________________________________________________________________________________