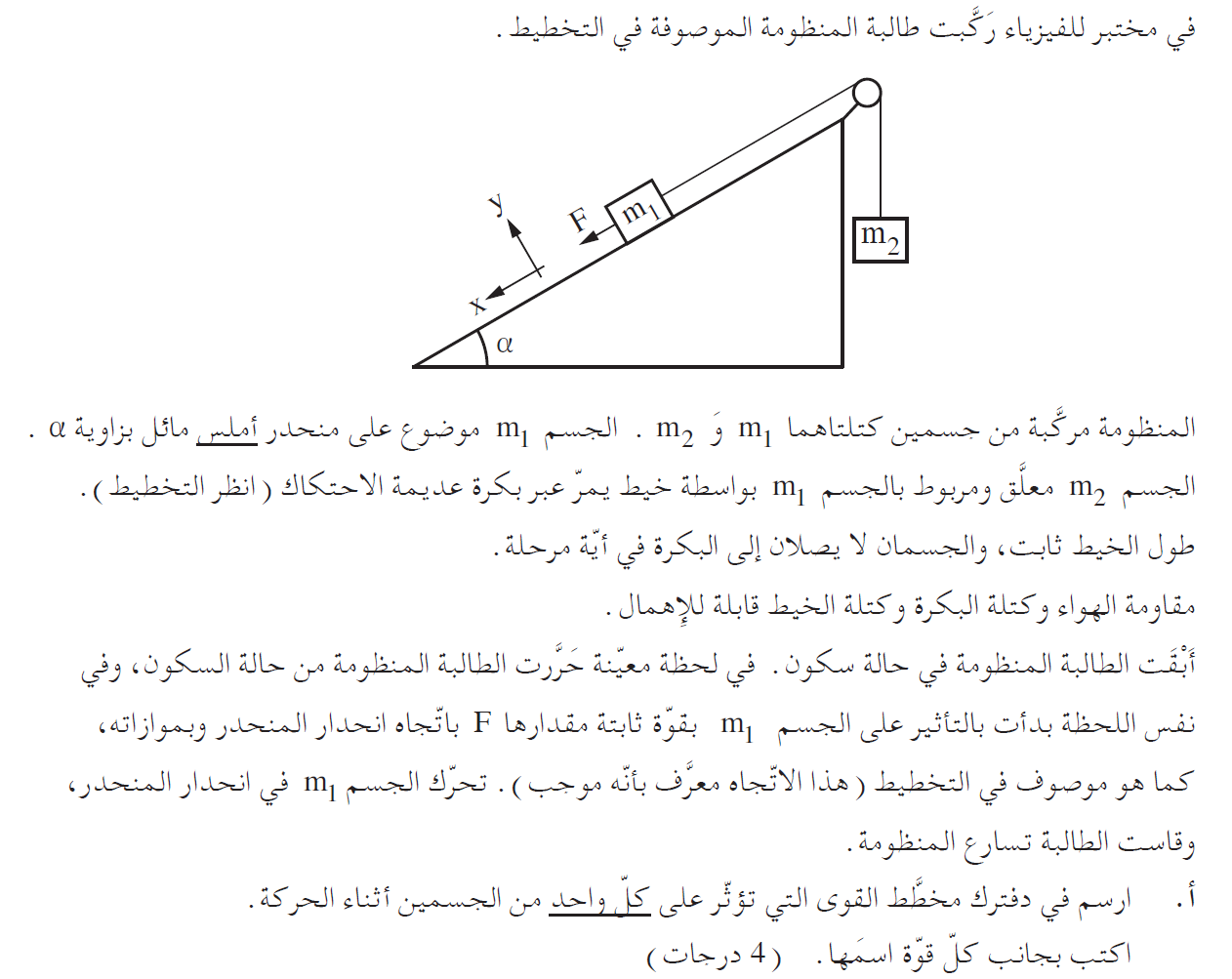
4. 2018,2 - حركة جسمان أحدهم موجود على سطح مائل
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
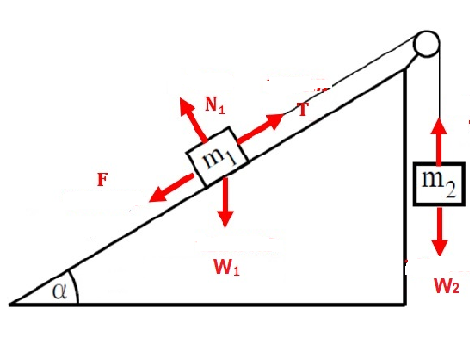
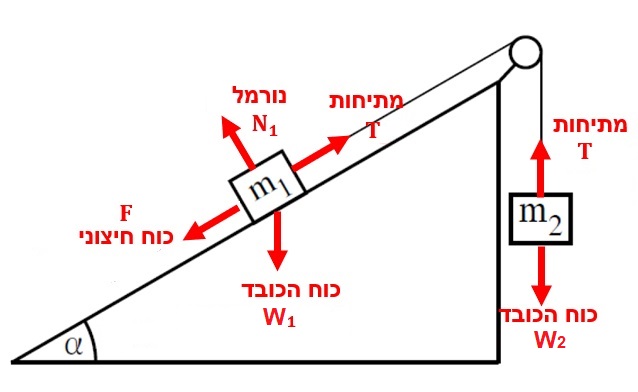
لحظة تأثير القوة F ، تبدأ الهيئة في التحرك من حالة السكون، ويتحرك الجسم المعلق من حالة السكون إلى أعلى، وبالتالي فأن القوة المحصّلة تعمل نحو الأعلى.
والجسم الموضوع على السطح المائل يتحرك من حالة السكون في اتجاه المنحدر، لأن القوة المحصّلة المؤثرة عليه تعمل في اتجاه المنحدر.
الخيط مربوط بين الجسمين ، والتوتر على امتداد الخيط نفسه، وبالتالي فإن قوة الشد المؤثرة على الجسم المعلق هي نفس قوة الشد المؤثرة على الجسم المُلقي على السطح المائل.
نضيف إلى الرسم هيئة المحاور .
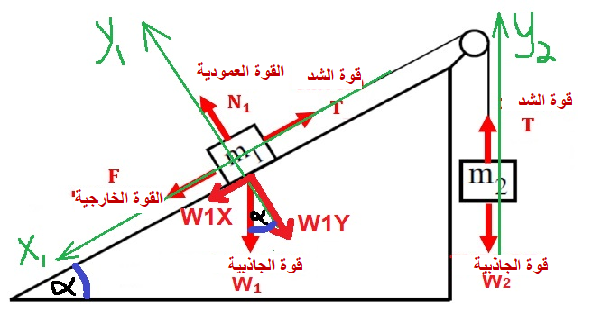
نكتب معادلة الحركة العمودية للجسم m2:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mspace linebreak=¨newline¨»«/mspace»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»a«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/menclose»«/mrow»«/mstyle»«/math»
نكتب معادلة الحركة للجسم m1, في اتجاه منحدر السطح المائل:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«msub mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»a«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
نكتب معادلة الحركة للجسم m1, في اتجاه عمودي للسطح المائل: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold-italic¨»Y«/mi»«/mrow»«/msub»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/mstyle»«/math»
- سرعة الجسمين في أي لحظة نفس المقدار، لذا فإن تسارع الجسمين متساوٍ : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mstyle»«/math»
سنكتب معادلات الحركة الثلاث في صورتها النهائية:
نكتب معادلة الحركة العمودية للجسم m2:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«/mstyle»«/math»
نكتب معادلة الحركة للجسم m1, في اتجاه منحدر السطح المائل:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
نكتب معادلة الحركة للجسم m1, في اتجاه عمودي للسطح المائل:«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/mstyle»«/math»
لتطوير تعبير للتسارع كدالة للقوة، نُعبّر عن التوتر بالخيط من معادلة حركة الجسم 2 ونّعوّض هذا التعبير في معادلة الحركة للجسم 1 في اتجاه منحدر السطح:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/mstyle»«/math»
نعوّض التعبير لقوة الشد: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/mstyle»«/math» بالمعادلة: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mstyle»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«/mstyle»«/math»
نُرتّب المعادلة ونعبّر عن التسارع منها:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»+«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«/mstyle»«/math»
______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
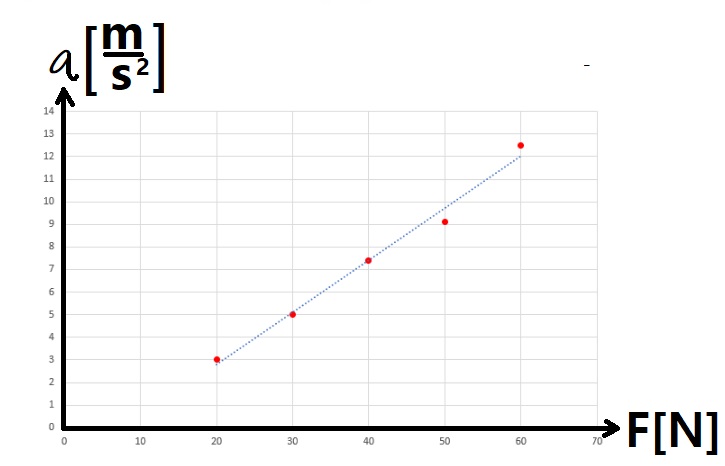
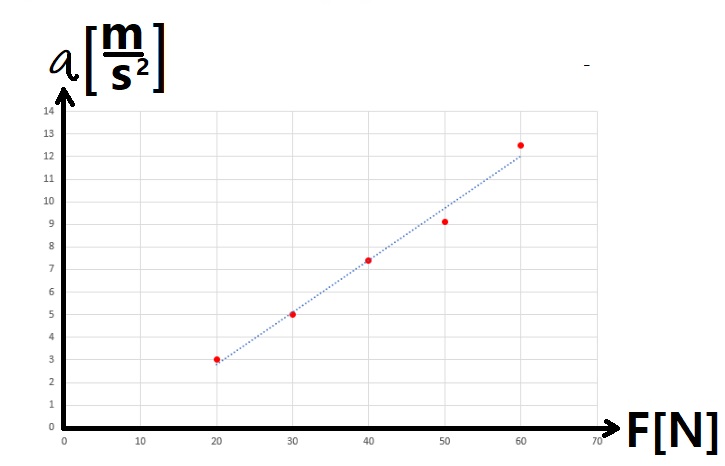
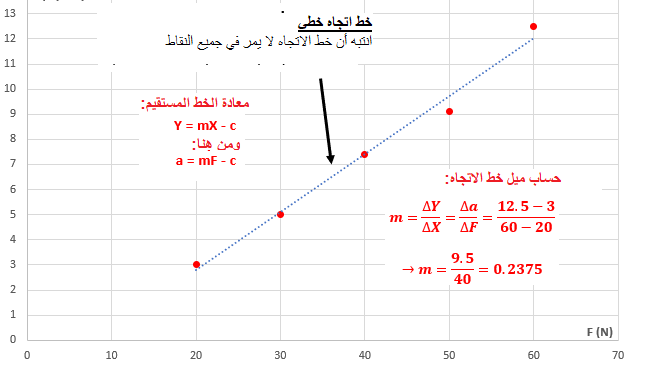
لحساب الكتلة m ، سنستخدم الدالة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/mstyle»«/math» والرسم البياني للدالة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/mstyle»«/math»
معامل F يعني ميل الرسم البياني ، وبالتالي فإن قيمة ميل الرسم البياني تساوي «math style=¨font-family:Arial¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathcolor=¨#0000FF¨»§#1605;§#1610;§#1604;«/mi»«mo mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/mstyle»«/math»
نحسب ميل خط الاتجاه في الرسم البياني:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1573;§#1578;§#1580;§#1575;§#1607;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1582;§#1591;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»F«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»12«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»60«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»20«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«mn mathvariant=¨bold¨»40«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2375«/mn»«mfrac mathcolor=¨#0000FF¨»«mstyle displaystyle=¨true¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«mi mathvariant=¨bold¨»N«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1573;§#1578;§#1580;§#1575;§#1607;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1582;§#1591;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2375«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mrow»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«/mstyle»«/math».
كتلتي الجسمين متساوية, لذا: m1=m2 نُشير إلى كتلة كل جسم بواسطة m، ونجد قيمة m، باستخدام ميل الرسم البياني:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2375«/mn»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2375«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»kg«/mi»«/msub»«/mstyle»«/math»
______________________________________________________________________________________

______________________________________________________________________________________
لكي تتحرك الهيئة في حركة منتظمة السرعة ، يجب أن تكون قيمة التسارع للمجموعة صفرًا.
نجد القوة F التي يكون بها التسارع يساوي صفرًا ، هذه القيمة تساوي قيمة نقطة تقاطع الدالة مع المحور الأفقي F .
نجد معادلة الدالة:
حسب ميل خط الاتجاه ، تكون معادلة خط الاتجاه هي: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2375«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»n«/mi»«/math»
نُعوّض أحد النقاط «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»60«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math» في معادلة خط الاتجاه ونجد الحد الحر n:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»23«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»n«/mi»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»23«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»60«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»n«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»n«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»23«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»60«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»13«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»n«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/math»
لذا، معادلة خط الاتجاه: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»23«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«/mstyle»«/math»
نجد من معادلة الخط المستقيم قيمة F التي فيها تساوي قيمة a صفرًا:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»23«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mspace linebreak=¨newline¨»«/mspace»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»23«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mspace linebreak=¨newline¨»«/mspace»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»23«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»23«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»82«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
لذلك عندما تكون قيمة القوة F تساوي 7.82 نيوتن ، ستتحرك المجموعة بسرعة ثابتة.
______________________________________________________________________________________