حلول ومنتديات لألبوم الحلول - الكينماتيكا في المستوى

______________________________________________________________________________________

• مجلد
• الجواب النهائي
• استراتيجية
• الحل اكامل
• انتبهوا

...

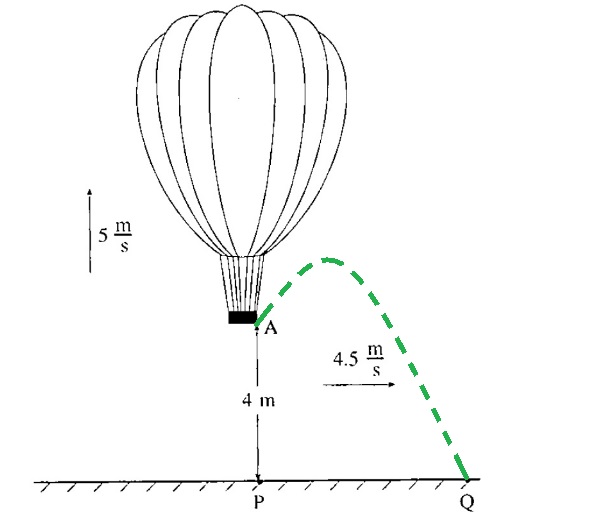
يتم تحرير الحجر من السلة ولا يتم رميه منه ، يجب التعامل مع حركة الحجر كحركة بالستية - رمي بزاوية ، وسرعة الرمي تساوي سرعة السلة في اللحظة التي يتم تحرير الحجر من السلة.

عندما يتم تحرير الحجر من السلة ، فإنه يتحرك في حركة بالستية. سرعة رمي الحجر تساوي سرعة السلة عندما ينفصل عنها. للسلة سرعة أفقية إلى اليمين وسرعة رأسية لأعلى ، لذلك يجب التعامل مع حركة الحجر على أنها رمي بزاوية فوق الأفق. سنصف حركة الحجر في مخطط عن مُقرّب:

1. بالنسبة للمراقب في السلة، يتم تحرير الحجر من السلة. بالنسبة للمراقب على الأرض ، يتم رمي الحجر بزاوية فوق الأفق.

2. بشكل عام، عندما يكون مطلوبًا وصف مسار الحركة، يجب وصف مسار الحركة بالنسبة إلى المراقب على الأرض.

3. للإجابة على هذا السؤال ، يجب وصف المسار الباليستي للرمي بزاوية فوق الأفق بشكل تقريبي. يجب أن يبدأ المسار في النقطة A وينتهي في النقطة Q. 

2. באופן כללי , כאשר נדרש לתאר מסלול תנועה , יש לתאר את מסלול התנועה ביחס למתבונן הנמצא בקרקע.

3. כדי לענות על שאלה זו יש לתאר בקירוב מסלול בליסטי של זריקה בזווית מעל האופק. המסלול צריך להתחיל בנקודה A , ולהסתיים בנקודה Q. 

______________________________________________________________________________________

______________________________________________________________________________________

• مجلد
• الجواب النهائي
• استراتيجية
• الحل الكامل
• انتبهوا

______________________________________________________________________________________

______________________________________________________________________________________

• مجلد
• الجواب النهائي
• استراتيجية
• الحل الكامل
• انتبهوا

...

زاوية اصطدام الحجر بسطح الأرض 66.27 درجة ، تحت الأفق.

اتجاه الحركة هو في اتجاه متجه السرعة. لإيجاد اتجاه متجه السرعة ، يجب أن نجد مركّب متجه السرعة في الاتجاه الأفقي، ومركّب متجه السرعة في الاتجاه الرأسي، والمتجه المحصّل لهذين المركّبين في أي لحظة - هو السرعة مقدارًا وتجاهًا. 

نجد مركب السرعة الأفقية ومركب السرعة الرأسية لحظة اصطدام الحجر بالأرض.

لا تتغير السرعة الأفقية في الحركة الباليستية، وفي هذه الحالة تساوي السرعة الأفقية 4.5 متر في الثانية، واتجاهها نحو اليمين.

وجدنا السرعة الرأسية في لحظة اصطدام الحجر بالأرض في القسم السابق ، وكان مقدارها 10.24 مترًا في الثانية واتجاهها نحو  الأسفل. 

نرسم مخططًا لمتجهات السرعة، ونرمز للزاوية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«/mstyle»«/math» بين اتجاه متجه السرعة  بالنسبة إلى الأفق في الرسم التخطيطي 

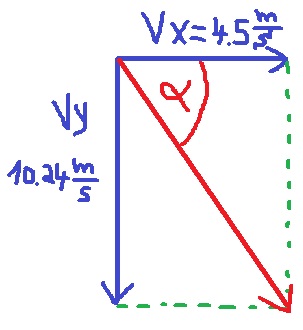
نجد الزاوية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«/mstyle»«/math»  بواسطة النسبة المثلثية الظل:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»24«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»66«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»27«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#176;«/mo»«/math»

لذلك ، فإن اتجاه حركة الحجر هو 66.27 درجة تحت الأفق.

המהירות האופקית בתנועה בליסטית לא משתנה, במקרה זה המהירות האופקית שווה ל 4.5 מטר לשנייה , וכיוונה ימינה.

את המהירות האנכית ברגע פגיעת האבן בקרקע מצאנו בסעיף קודם , גודלה 10.24 מטר לשנייה וכיוונה כלפי מטה.

נערוך תרשים לווקטורי המהירויות , ונסמן בתרשים את כיוון ווקטור המהירות השקולה יחסית לאופק  ב «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«/mstyle»«/math» , כיוון זה הוא כיוון זווית הפגיעה המבוקש:

נמצא את «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«/mstyle»«/math»  בעזרת זהות הטנגנס:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»24«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»66«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»27«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#176;«/mo»«/math»

לכן, כיוון תנועת האבן הוא 66.27 מעלות מתחת לאופק.

في جميع الحالات التي نتعامل فيها مع إصابة أو ضربة، يكون المعنى جزءًا من الثانية قبل الضربة وليس بعده ، لذلك تظل مسألة لحظة تكون فيها حركة الحجر بالستية. 

______________________________________________________________________________________

______________________________________________________________________________________

• مجلد
• الجواب النهائي
• استراتيجية
• الحل الكامل
• انتبهوا

______________________________________________________________________________________