7. 1993,1- الرمي الأفقي
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»3«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mrow»«/mstyle»«/math»
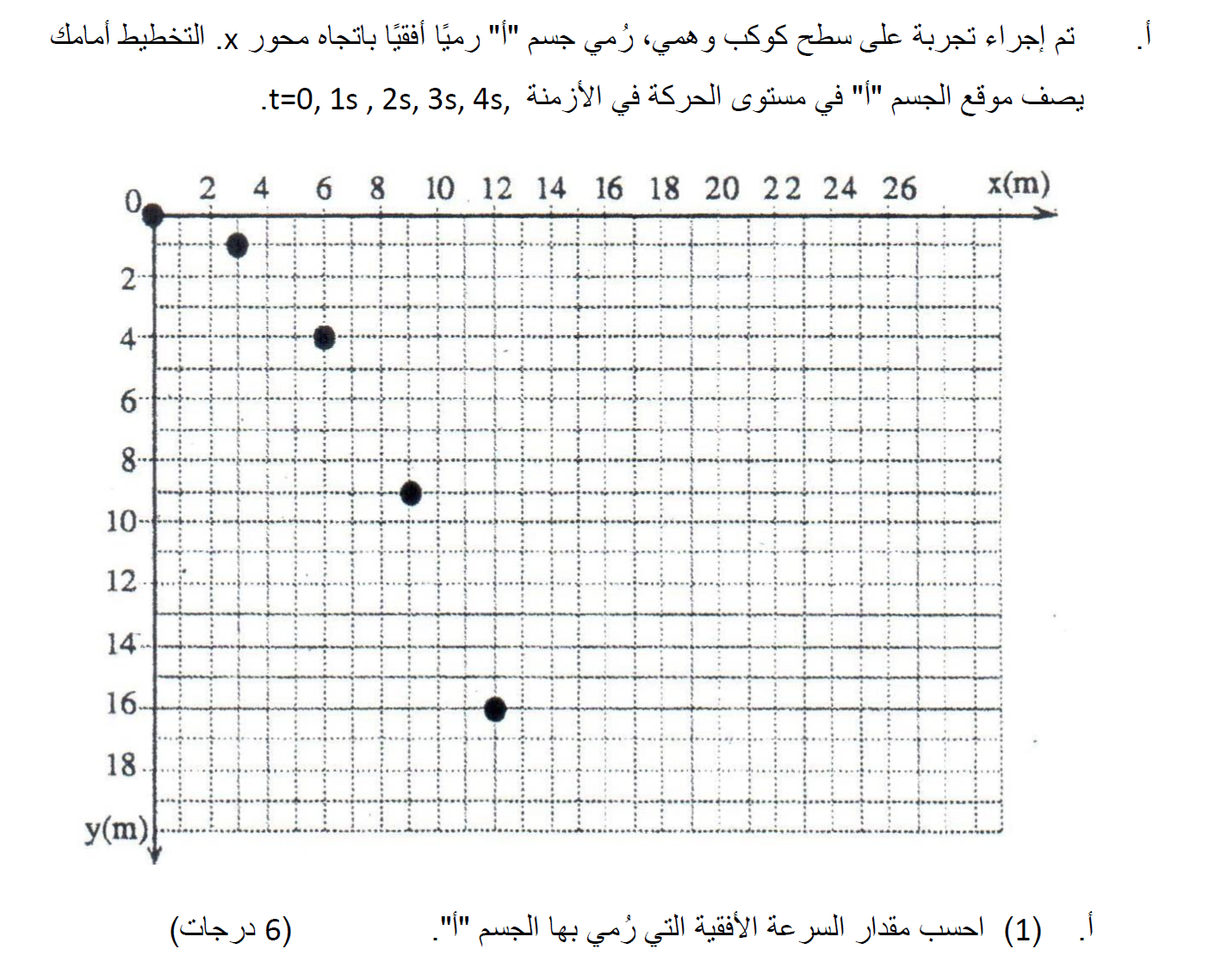
في الحركة الباليستية ، لا تتغير السرعة الأفقية للجسم، وهي تساوي السرعة الأفقية لحظة رميه.
من مخطط التتبع يمكن رؤية أن الجسم يتقدم 3 أمتار كل ثانية في الاتجاه الأفقي. لذلك سرعته الأفقية هي 3 أمتار في الثانية، وهي أيضًا سرعة الرمي.
على الرغم من أن مخطط التتبع يحتوي على 5 نقاط فقط، ولكن باستخدام المبادئ الفيزيائية ، يمكن إيجاد أي مُعطى للحركة في أي لحظة وفي أي موقع ، فقط بناءً على موقع النقاط في الرسم التخطيطي.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»*«/mo»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»2«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
يوجد على سطح كل كوكب يوجد تسارع جاذبية ثابت ، وخاص بالكوكب.
כאשר גוף נע בתאוצה קבועה מהירותו הממוצעת שווה למהירות באמצע הזמן.
ניתן לחשב את המהירות במספר נקודות, ותאר את התנועה בגרף מהירות בתלות בזמן, שיפוע הגרף שווה לתאוצת הגוף.
لإيجاد تسارع الجاذبية على سطح الكوكب، نشير إلى الحركة الرأسية.
متوسط السرعة في كل مقطع من الحركة يساوي السرعة اللحظية في منتصف الفترة الزمنية في مقطع الحركة هذا.
نجد السرعة اللحظية في الاتجاه الرأسي في النقاط 2،3،4.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨top¨»«mi mathvariant=¨bold¨»V«/mi»«/menclose»«msub mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»Y«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»4«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨top¨»«mi mathvariant=¨bold¨»V«/mi»«/menclose»«msub mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»Y«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»8«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨top¨»«mi mathvariant=¨bold¨»V«/mi»«/menclose»«msub mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»Y«/mi»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
تزداد السرعة في كل ثانية بمقدار 2 متر في الثانية. إذن ، فإن تسارع الجسم تساوي مترين لكل ثانية مربعة.
يمكنك وصف الحركة في الرسم البياني للسرعة كدالة للزمن، وحساب ميل الرسم البياني ، قيمة ميل الرسم البياني هو 2 متر لكل ثانية مربعة.
המהירות הממוצעת בכל קטע של התנועה שווה למהירות הרגעית באמצע הזמן של אותו קטע תנועה .
נמצא את המהירות הרגעית בכיוון האנכי ברגע סימון נקודות 2,3,4 .
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨top¨»«mi mathvariant=¨bold¨»V«/mi»«/menclose»«msub mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»Y«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»4«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨top¨»«mi mathvariant=¨bold¨»V«/mi»«/menclose»«msub mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»Y«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»8«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨top¨»«mi mathvariant=¨bold¨»V«/mi»«/menclose»«msub mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»Y«/mi»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
המהירות גדלה בכל שנייה ב 2 מטר לשנייה. לכן תאוצת הגוף היא 2 מטר לשנייה בריבוע.
אפשר לתאר את התנועה בגרף מהירות בתלות בזמן , ולחשב את שיפוע הגרף, ערך שיפוע הגרף הוא 2 מטר לשנייה בריבוע.
1. لا يمكن إيجاد سرعة في النقطتين الأولى والأخيرة. في هذه الحالة يجب أن تستند الإجابة على ثلاث نقاط فقط.
2. الطالب الذي يحل السؤال باستخدام الدوال الحركية بناءً على نقطة واحدة فقط ، لن تعتبر الإجابة إجابة كاملة.
حتى لو كانت الإجابة النهائية هي نفسها.
3. يُتّبع أن يُشار إلى تسارع الجاذبية على سطح الأرض بالحرف g ، وأن يُشار إلى تسارع الجاذبية على سطح أي كوكب آخر بعلامة * g
إضافة علامة النجمة هي للتمييز بين تسارع الجاذبية على سطح الكوكب وتسارع الجاذبية على سطح الأرض.
2. תלמיד שיפתור את השאלה בעזרת פונקציות הקינמטיקה על סמך נקודה אחת בלבד , תשובה לא תחשב לתשובה מלאה.
גם אם התשובה הסופית תהיה זהה.
3. את תאוצת הכובד על כדור הארץ מקובל לסמן באות g , את תאוצת הכובד על פני כל כוכב אחר מקובל לסמן ב *g
תוספת הכוכבית, היא כדי להבחין בין תאוצת הכובד על פני כוכב הלכת לתאוצת הכובד על פני כדור הארץ.
______________________________________________________________________________________

______________________________________________________________________________________
...
نرسم مخطط التتبع للجسم "ب" بنقاط حمراء. ومخطط التتبع للجسم "جـ" بالنقاط الخضراء.
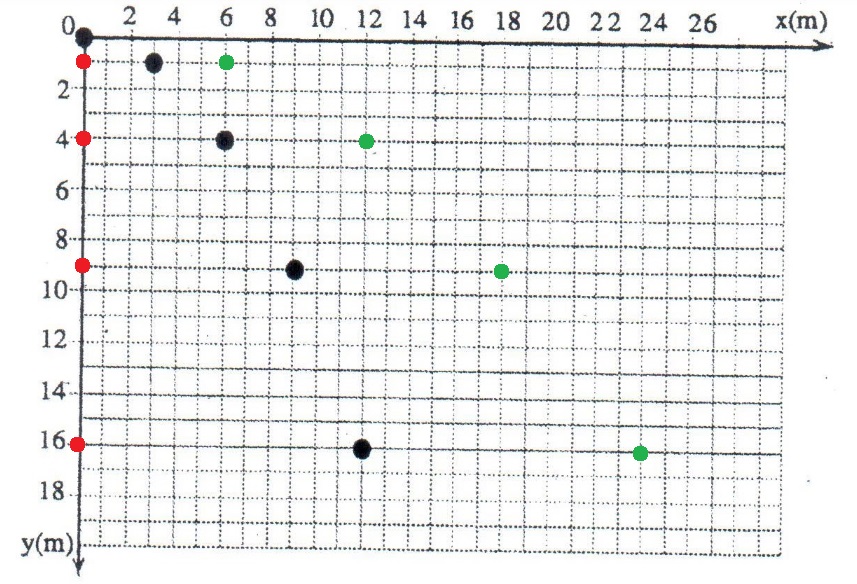

تتحرك الأجسام الثلاثة في حركات رأسية متطابقة، وفي الاتجاه الأفقي تتحرك الأجسام الثلاثة بسرعات ثابتة، مختلفة المقدار.
في الاتجاه العمودي تتحرك الأجسام الثلاثة من حالة السكون بتسارع الجاذبية إلى أسفل، يكون الموقع الرأسي للجسم "ب" و "ج" هو نفس الموقع الرأسي للجسم "أ" في أي لحظة.
يتم تحديد المواقع الأفقية وفقًا لمقدار السرعة الأفقية لكل جسم. يتحرك الجسم "ب" من حالة السكون ، وسرعته الأفقية تساوي صفرًا ، ولا يتحرك للأمام في الاتجاه الأفقي.
سرعة الجسم "ج" أفقية أكبر بمرتين من السرعة الأفقية للجسم "أ" ، وبالتالي فإن المسافة الأفقية التي يقطعها الجسم "ج" في كل ثانية أكبر بمرتين من المسافة الأفقية التي يقطعها الجسم "أ".
نرسم مخطط التتبع اللائم للجسم B بنقاط حمراء. ومخطط التتبع الملائم للجسم C بالنقاط الخضراء.
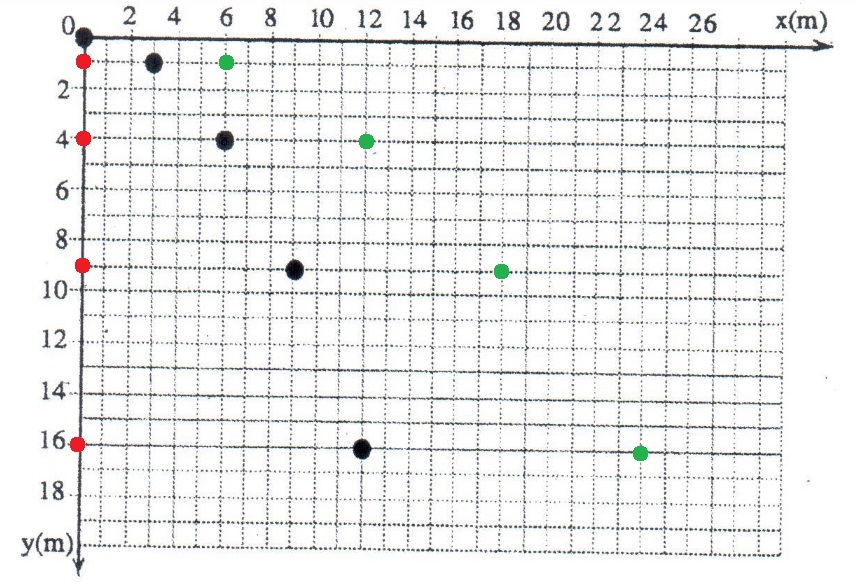
המיקומים האופקיים נקבעים בהתאם לגודל המהירות האופקית של כל אחד מהגופים. גוף ב' נע ממנוחה מהירותו האופקית אפס, הוא לא מתקדם בכיוון האופקי.
לגוף ג' מהירות אופקית גדולה פי 2 מהמהירות האופקית של גוף א' , לכן המרחק האופקי שעובר גוף בכל שניה ג' גדול פי 2 , מהמרחק האופקי שעובר גוף א'.
في السؤال مكتوب أن الجسم "ب" يتحرك في السقوط الحر. القصد هنا أن الجسم بدأ التحرك من حالة السكون ، والسقوط الحر هو أي حركة تحت تأثير الجاذبية فقط.
أي جسم يقذف لأعلى يتحرك أيضًا من لحظة الرمي حركة في السقوط الحر.
גם גוף הנזרק כלפי מעלה נע מרגע הזריקה בנפילה חופשית.
______________________________________________________________________________________

______________________________________________________________________________________
...
من تعريف التسارع ، يكون اتجاه متجه تغيّر السرعة هو نفسه اتجاه التسارع ، وتتحرك جميع الأجسام التي تتحرك في السقوط الحر في تسارع ثابت نحو الأسفل - تسارع الجاذبية.
للإجابة على هذا القسم، انظر إلى جميع القوانين والتعريفات التي يظهر فيها متجه تغيّر السرعة. في هذه الحالة من السهل شرح ذلك من خلال تعريف التسارع.
من تعريف التسارع ، يكون اتجاه متجه تغيُّر السرعة هو نفسه اتجاه التسارع :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mover»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/math»
من تعريف التسارع ، يكون اتجاه متجه التسارع هو نفسه اتجاه متجه تغيُّر السرعة.
تتحرك جميع الأجسام التي تتحرك في حالة السقوط الحر بتسارع ثابت نحو الأسفل - تسارع الجاذبية. لذلك ،فإن اتجاه متجه تغيُّر السرعة يكون إلى أسفل.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mover»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/math»
מהגדרת התאוצה כיוון ווקטור התאוצה הוא ככיוון ווקטור שינוי המהירות.
כל הגופים הנעים בנפילה חופשית , נעים בתאוצה קבועה כלפי מטה - תאוצת הכובד. לכן גם כיוון ווקטור שינוי המהירות כיוונו כלפי מטה.
1. السؤال هو سؤال عام وليس له علاقة خاصة بالأقسام السابقة.
2. عمليات المتجه هي عمليات أولية وأساسية وهامة ، ولا نستخدمها غالبًا ، ولكنها مهمة جدًا.
3. يجب التمييز بين متجه تغيُّر السرعة ومتجه السرعة.
______________________________________________________________________________________