3. 2007,3- الرمي بزاوية ، الرسم البياني VX VY
______________________________________________________________________________________
...
فوق الأفق
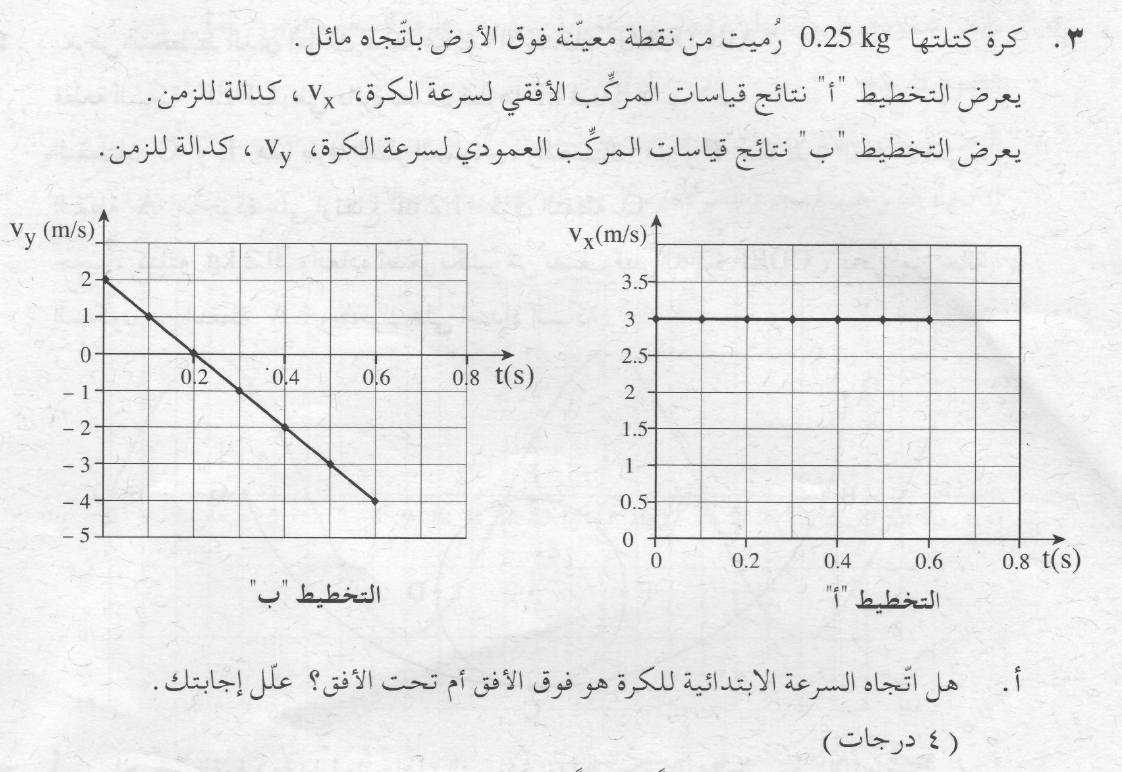
في جزء من الزمن تكون السرعة سالبة وفي جزء آخر تكون موجبة، غيرت الكرة اتجاه حركتها، لذا بالتأكيد تم رمي الكرة نحو الأعلى.
في الرسم البياني للسرعة العمودية كدالة للزمن، جزء من الزمن تتحرك فيه الكرة بسرعة عمودية موجبة وجزء آخر تتحرك فيه الكرة بسرعة عمودية سالبة.
هذا يعني أن الكرة غيّرت اتجاه حركتها، وبالتالي فإن حركة الكرة في الاتجاه العمودي هي رمي عمودي لأعلى. لذا يتم رمي الكرة فوق الأفق.
(إذا كان اتجاه رمي الكرة أسفل الأفق، في الاتجاه العمودي لن يتغير اتجاه الحركة، ستكون الحركة العمودية رمي عمودي لأسفل).
הגוף שינה את כיוון תנועתו ,לכן תנועת הכדור בכיוון האנכי היא זריקה אנכית כלפי מעלה. הכדור נזרק מעל האופק.
(אם כיוון זריקת הכדור היה מתחת לאופק , בכיוון האנכי כיוון התנועה לא היה משתנה, התנועה האנכית הייתה זריקה אנכית כלפי מטה).
1. يتم تعريف كل حركة نسبة لمحور الحركة، في هذا السؤال لم يتم تحديد محور الحركة بشكل صريح. لذلك ، من حقيقة أن سرعة الكرة في البداية موجبة، لا يمكن معرفة اتجاه الحركة. ولكن في الحركة العمودية نرى أن في جزء من الزمن تكون السرعة موجبة وجزءًا من الزمن تكون السرعة سالبة ، يمكن القول على وجه اليقين أن الاتجاه العمودي للحركة قد تغيّر، وتتحرك الكرة في الاتجاه العمودي في رمي نحو الأعلى، يكون اتجاه رمي الكرة فوق الأفق.
2. يتناول أحد الرسمين الحركة الأفقية ويتناول الرسم البياني الآخر الحركة العمودية، قبل البدء في الحل، من المهم محاولة رؤية الصورة الكاملة ومحاولة فهم الحركة البالستية للكرة، وأحيانًا بضع ثوانٍ أخرى من يساعد الفهم الجيد للحركة في الوصول إلى الاستنتاج الصحيح ، وامنح نفسك الوقت للتفكير وفهم الحركة الكاملة ، بما يتجاوز المعطيات التي تظهر في السؤال.
2. גרף אחד עוסק בתנועה האופקית והגרף השני עוסק בתנועה האנכית, לפני תחילת הפתרון חשוב לנסות לראות את התמונה המלאה לנסות להבין את התנועה הבליסטית של הכדור, לפעמים עוד כמה שניות של הבנה טובה של התנועה עוזרת להגיע למסקנה הנכונה , תנו לעצמכם את הזמן לחשוב ולהבין את התנועה המלאה ,מעבר לנתונים המופיעים בשאלה.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math» , باتجاه 33.69 درجة فوق الأفق.
متجه سرعة الرمي هو المتجه المحصّل لمتجه السرعة الأفقية ومتجه السرعة العمودية.
متجه سرعة الرمي يساوي محصّلة مركب السرعة الأفقية ومركب السرعة العمودية.
نستخدم طريقة المتوازي الأضلاع لإيجاد متجه السرعة الابتدائية:
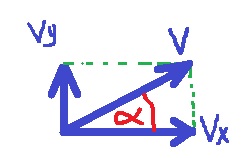
نجد مقدار السرعة الابتدائية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«msup»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«msup»«mn mathvariant=¨bold¨»2«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»13«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
نجد اتجاه السرعة الابتدائية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»69«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#176;«/mo»«mspace linebreak=¨newline¨»«/mspace»«/math»
והוא שקול לרכיב המהירות האופקית ולרכיב המהירות האנכית.
נשתמש בשיטת המקבילית כדי למצוא את ווקטור המהירות ההתחלתית:

נמצא את גודל המהירות ההתחלתית :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«msup»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«msup»«mn mathvariant=¨bold¨»2«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»13«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
נמצא את כיוון התנועה ההתחלתי:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»69«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#176;«/mo»«mspace linebreak=¨newline¨»«/mspace»«/math»
حتى لو لم يتم كتابة المقدار والاتجاه بين قوسين، يجب دائمًا عند حساب المتجه أن تحسب كلًا من مقداره واتجاهه.
______________________________________________________________________________________

______________________________________________________________________________________
...
من ارتفاع 0.6 متر.
1. يمكن إيجاد إزاحة الجسم نحو الأعلى والإزاحة نحو الأسفل من الرسم البياني VY. وبمساعدة هذه الإزاحات يمكن إيجاد من أي ارتفاع تم رمي الجسم.
2. من لحظة رمي الكرة حتى وصولها إلى الأرض، تتحرك بتسارع ثابت يمكن كتابة دالة الموقع كدالة للزمن لمركّبة الحركة الرأسية وبوسطة هذه الدالة يمكن إيجاد الارتفاع الذي رُميت منه الكرة.
2. מרגע שהכדור נזרק ועד שהוא מגיע לקרקע הוא נע בתנועה בתאוצה קבועה , אפשר לכתוב פונקציית מקום זמן לתנועה האנכית ולמצוא בעזרת הפונקציה את הגובה ממנו נזרק הכדור.
لإيجاد الارتفاع الذي رُميت منه الكرة ، نحسب إزاحة الكرة نحو الأعلى وإزاحة الكرة نحو الأسفل من الرسم البياني للسرعة العمودية كدالة للزمن:
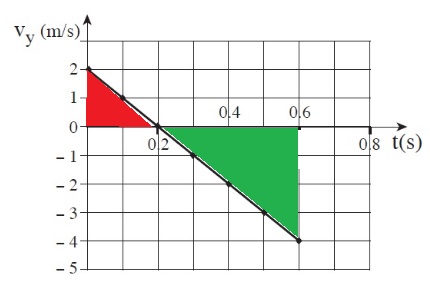
عندما تكون سرعة الكرة موجبة ، تتحرك الكرة في اتجاه المحور نحو الأعلى.
المساحة المحصورة بين الدالة والمحور الزمني تساوي إزاحة الحركة لأعلى، وهذه المساحة المشار لها في الرسم البياني باللون الأحمر:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfenced mathcolor=¨#0000FF¨ open=¨|¨ close=¨|¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»Y«/mi»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
نحسب بطريقة مماثلة إزاحة الحركة من نقطة قمة الارتفاع ، حتى تصل الكرة إلى الأرض:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfenced mathcolor=¨#0000FF¨ open=¨|¨ close=¨|¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»Y«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
من حساب الإزاحة، نرى أن الكرة ترتفع من نقطة الرمي 20 سم لتصل إلى قمة ارتفاعها، ثم تنزل الكرة من القمة إلى سطح الأرض بمقدار 80 سم.
نصف حركة الكرة من لحظة الرمي حتى لحظة اصطدامها بالأرض في المخطط التالي:
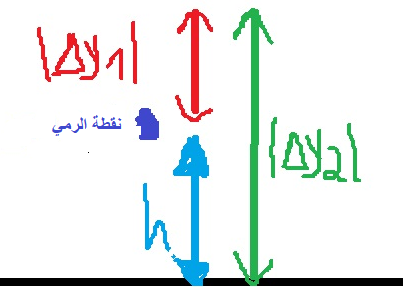
من المخطط يمكن فهم العلاقة بين الإزاحة الرأسية والارتفاع الذي تم رمي الكرة منه:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
لذلك ، يتم رمي الكرة من ارتفاع 0.6 متر.
طريقة أخرى: نُعرّف محور حركة نقطة أصله على سطح الأرض وموجهًا نحو الأعلى، كما هو موضّح في الشكل التالي:
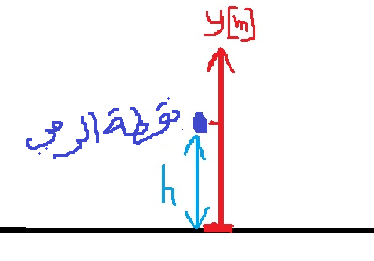
بالنسبة إلى هذا المحور ، فإن الموقع الابتدائي يساوي الارتفاع الذي تُرمى منه الكرة. والموقع النهائي للكرة هو صفر.
اتجاه محور الحركة إلى الأعلى، وبالتالي فإن التسارع سالب.
من الرسم البياني للسرعة العمودية كدالة للزمن، يمكن فهم أنه من لحظة رمي الكرة حتى وصولها إلى الأرض ، مرّ 0.6 ثانية.
نكتب دالة المكان كدالة للزمن ونجد الارتفاع الابتدائي حسب هذه الدالة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»y«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«mrow»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«msup mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mspace linebreak=¨newline¨»«/mspace»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/mstyle»«/math»

כאשר מהירות הכדור חיובית, הכדור נע בכיוון התיר , כלפי מעלה .
השטח התחום בין הפונקציה לציר הזמן שווה להעתק התנועה כלפי מעלה , שטח זה מסומן בגרף באדום:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfenced mathcolor=¨#0000FF¨ open=¨|¨ close=¨|¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»Y«/mi»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
נחשב באופן דומה את העתק התנועה מנקודת שיא הגובה , ועד שהכדור מגיע לקרקע:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfenced mathcolor=¨#0000FF¨ open=¨|¨ close=¨|¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»Y«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
מחישוב העתקים ניתן להבין שהכדור עולה מנקודת הזריקה ועד לשיא הגובה 20 ס"מ. ולאחר מכן יורד הכדור מנקודת שיא הגובה ועד לקרע 80 ס"מ.
נתאר את תנועת הכדור מרגע הזריקה ועד לרגע הפגיעה בקרקע בתרשים כללי:
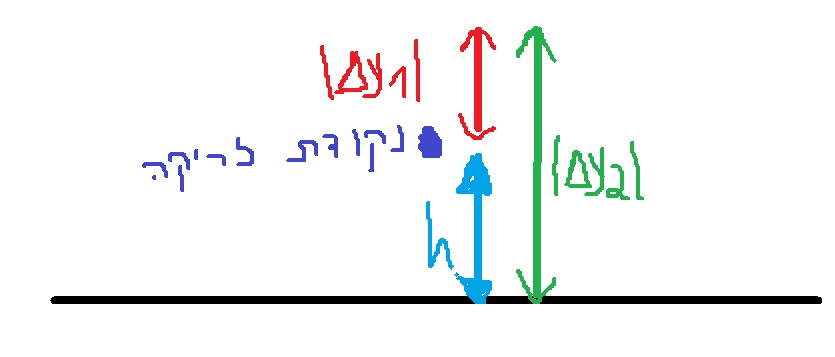
מהתרשים ניתן להבין את הקשר שבין ההעתקים האנכיים לבין הגובה ממנו נזרק הכדור:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
לכן , הכדור נזרק מגובה של 0.6 מטרים.
דרך נוספת: נגדיר ציר תנועה שראשיתו בקרקע וכיוונו כלפי מעלה, כמוראה באיור הבא:
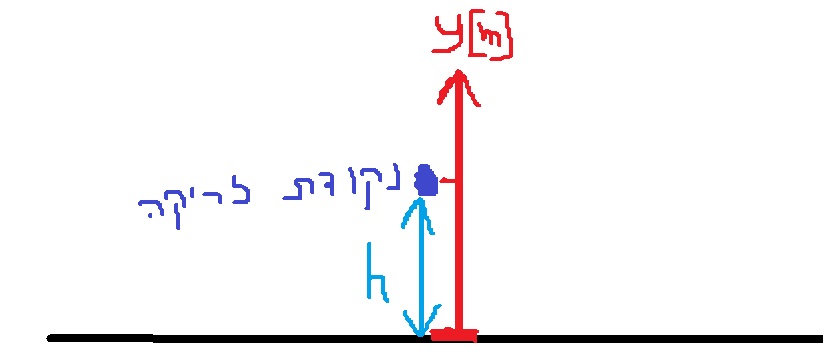
ביחס לציר זה , המיקום ההתחלתי שווה לגובה ממנו ניזרק הכדור. והמיקום הסופי של הכדור הוא אפס.
כיוון ציר התנועה הוא כלפי מעלה , לכן התאוצה שלילית.
מגרף המהירות האנכית בתלות בזמן ניתן להבין שמרגע שהכדור נזרק ועד שהגיע לקרקע עברו 0.6 שניות.
נכתוב את פונקציית המקום בתלות בזמן לתיאור תנועת הכדור, ונמצא מהפונקציה את הגובה ההתחלתי:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»y«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«mrow»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«msup mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mspace linebreak=¨newline¨»«/mspace»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/mstyle»«/math»
1. عند استخدام الرسم البياني للسرعة كدالة للزمن لإيجاد الإزاحة، من السهل ارتكاب خطأ ، فمن الأفضل حساب المساحة دون الإشارة الجبرية، وبعد ذلك نحدد الإشارة وفقًا للحركة.
2. يجب أن نُفرّق بين الارتفاع والموقع، يتم تحديد الارتفاع فقط بالنسبة إلى سطح الأرض،بينما يحدد الموقع بالنسبة إلى نقطة أصل محور الحركة.
2. חשוב להבחין בין גובה למיקום, הגובה נקבע רק ביחס לקרקע , מיקום נקבע ביחס לראשית ציר התנועה.
______________________________________________________________________________________

* القسمان D و E مشمولان في موضوعا الديناميكا والطاقة، ولا يمكن الإجابة على هذه الأقسام بمساعدة الكينماتيكا وحده.