______________________________________________________________________________________
...
متوسط السرعة هي سرعة ثابتة ، وهي تمثل الحركة بسرعة متغيرة ، ويتم تحديدها وفقًا للنسبة بين الإزاحة الكلية التي يقطعها الجسم في حركته والزمن الكلي للحركة.
من المهم فهم معنى متوسط السرعة ومعرفة تعريفها.
متوسط السرعة هي سرعة ثابتة ، وهي تمثل الحركة بسرعة متغيرة ، ويتم تحديدها وفقًا للنسبة بين الإزاحة الكلية التي يقطعها الجسم في حركته والزمن الكلي للحركة.
لم تتم كتابة تعريف متوسط السرعة في أوراق القوانين المرفقة لإمتحان البجروت.
______________________________________________________________________________________

______________________________________________________________________________________
...
مساويًا لها
يمكنك حساب مقدار السرعة المتوسطة ، أو إظهار أن متوسط السرعات متساوي بشكل عام.
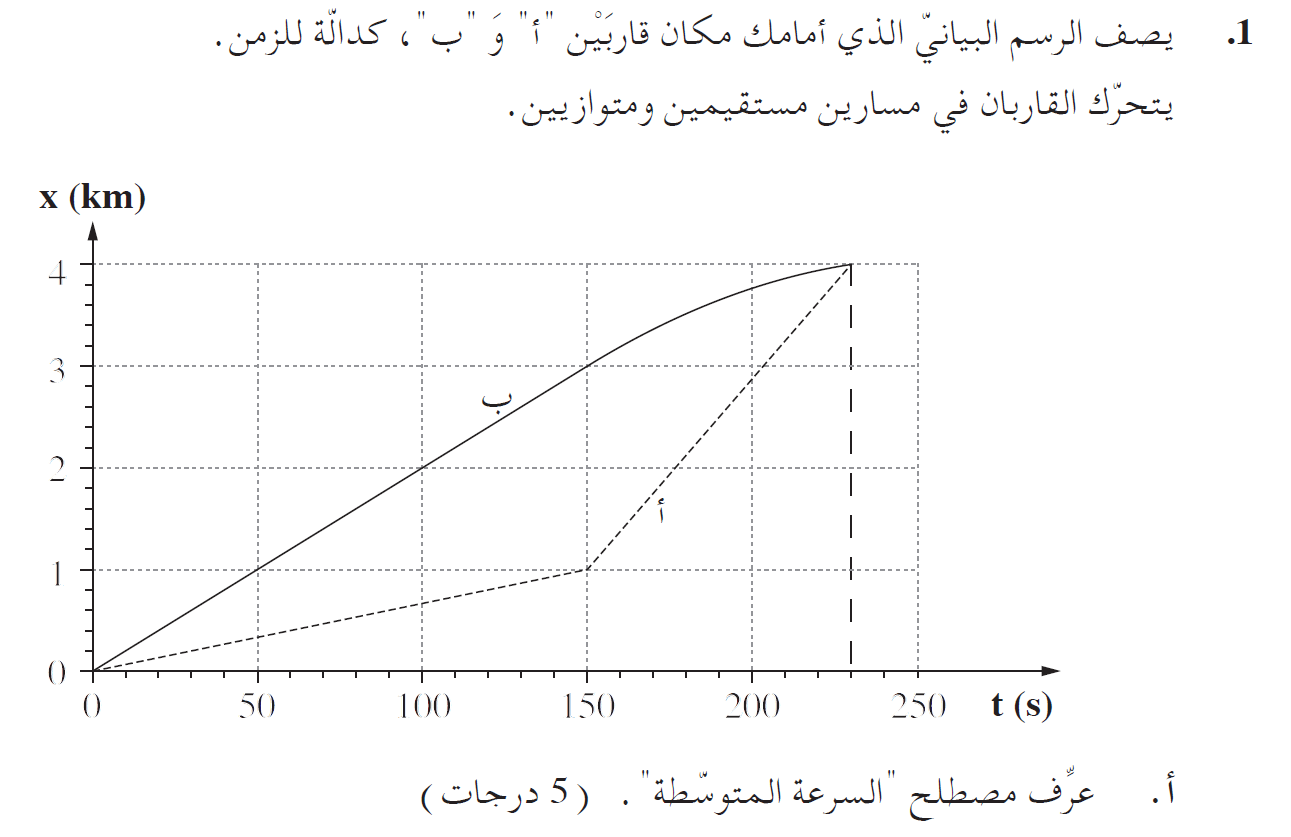
يقطع القاربان إزاحات متساوية مقدار كل منها 4 كيلومترات في نفس الفترة الزمنية للحركة البالغة 230 ثانية ، وبالتالي فإن متوسط سرعة القاربين هو نفسه حسب التعريف.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨top¨»«menclose notation=¨top¨»«mi mathvariant=¨bold¨»V«/mi»«/menclose»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#1499;§#1493;§#1500;§#1500;«/mi»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»§#1499;§#1493;§#1500;§#1500;«/mi»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/mstyle»«/math»
לשתי הסירות מהירות ממוצעת זהה.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨top¨»«menclose notation=¨top¨»«mi mathvariant=¨bold¨»V«/mi»«/menclose»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#1499;§#1493;§#1500;§#1500;«/mi»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»§#1499;§#1493;§#1500;§#1500;«/mi»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/mstyle»«/math»
לשתי הסירות מהירות ממוצעת זהה.
في الرسم البياني للموقع كدالة للزمن، متوسط السرعة في مقطع حركة معين مساوٍ لميل الخط القاطع للدالة من نقطة البداية حتى نقطة النهاية للحركة .
לשתי הסירות יש מיתר זהה , עבור תנועתן ב 230 השניות הראשונות, לכן מהירותו הממוצעת היא זהה.
______________________________________________________________________________________

______________________________________________________________________________________
...
التسارع سالب.
في الرسم البياني للموقع كدالة للزمن، فإن ميل الرسم البياني يمثل السرعة. تسارع موجب عند زيادة السرعة ، وتسارع سالب عند انخفاض السرعة.
في هذه الثمانين ثانية ، يقل ميل الرسم البياني ، وبالتالي تقل سرعة القارب. والتسارع يكون سالبًا.
الرسم البياني للموقع كدالة للزمن غير خطي ، لكن التسارع ثابت.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1875«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mrow»«/mstyle»«/math»
في الثمانين ثانية الأخيرة ، يتحرك القارب "ب" بتسارع ثابت ، يمكنك معرفة معطيات الحركة في هذه الثمانين ثانية ، واستخدام إحدى الدوال الملائمة للحركة بتسارع ثابت لحساب تسارع القارب "ب" ، في الثمانين ثانية الأخيرة من حركتها .
.نتطرق إلى حركة القارب "ب" من اللحظة t = 150s حتى اللحظة t = 230s ، من خلال الرسم البياني يمكن ملاحظة أن الإزاحة هي 1000 متر ، وزمن الحركة 80 ثانية.
حتى اللحظة t = 150 ثانية ، يتحرك القارب بسرعة ثابتة. هذه السرعة هي السرعة التي بدأ بها القارب حركته المتسارعة. نحسب هذه السرعة من ميل الرسم البياني في أول 150 ثانية.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»v«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»3000«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»150«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»3000«/mn»«mn mathvariant=¨bold¨»150«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
نكتب معطيات الحركة المتسارعة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»v«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1000«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»80«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»?«/mo»«/math»
يمكنك إيجاد التسارع باستخدام دالة الموقع كدالة للزمن في الحركة المتسارعة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»v«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/math»
نعبّر عن التسارع:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathcolor=¨#0000FF¨»x«/mi»«mo mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mi mathcolor=¨#0000FF¨»x«/mi»«mn»0«/mn»«/msub»«mo mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mi mathcolor=¨#0000FF¨»v«/mi»«mn»0«/mn»«/msub»«mo mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathcolor=¨#0000FF¨»t«/mi»«mo mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn»1«/mn»«mn»2«/mn»«/mfrac»«mo mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathcolor=¨#0000FF¨»a«/mi»«mo mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathcolor=¨#0000FF¨»t«/mi»«mn»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«mo mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathcolor=¨#0000FF¨»x«/mi»«mo mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mi mathcolor=¨#0000FF¨»v«/mi»«mn»0«/mn»«/msub»«mo mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathcolor=¨#0000FF¨»t«/mi»«mo mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn»1«/mn»«mn»2«/mn»«/mfrac»«mo mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathcolor=¨#0000FF¨»a«/mi»«mo mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathcolor=¨#0000FF¨»t«/mi»«mn»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»(«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»v«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«msup»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
نعوّض معطيات الحركة في تعبير التسارع التي حصلنا عليها ، ونجد التسارع :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»(«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»v«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«msup»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»1000«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»80«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«msup»«mn mathvariant=¨bold¨»80«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1200«/mn»«/mrow»«mn mathvariant=¨bold¨»6400«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1875«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
بشكل عام ، من أجل حساب مُعطى معين للحركة ، يجب إيجاد نوع الحركة (سرعة ثابتة ، أو تسارع ثابت) جميع معطيات الحركة الممكنة ، واستخدام إحدى دوال الحركة ، لإيجاد مُعطى الحركة المطلوب.
______________________________________________________________________________________

______________________________________________________________________________________
...
في مقطع الحركة الأول ، يتحرك القارب "ب" بسرعة ثابتة ، وفي مقطع الحركة الثاني ، يتحرك القارب بتسارع ثابت.
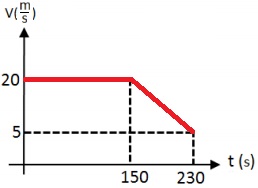
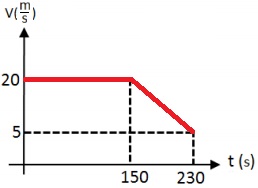
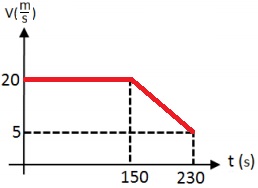
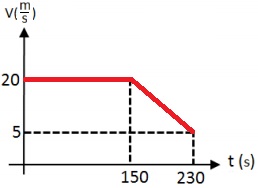
يتحرك القارب "ب" بسرعة ثابتة مقدارها 20 مترًا في الثانية. لمدة 150 ثانية.
بعد ذلك ،و لمدة 80 ثانية ، تحرك القارب "ب" بتسارع ثابت قدره 0.1875 مترًا لكل ثانية مربعة.
لوصف الرسم البياني بشكل كمي ، نجد سرعة القارب في اللحظة t = 230s.
نستخدم دالة السرعة كدالة للزمن لآخر 80 ثانية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1875«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»80«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mrow»«/mstyle»«/math»
لذلك وصف الرسم البياني هو:
לאחר מכן במשך 80 שניות נעה סירה ב' בתאוצה קבועה שגודלה 0.1875- מטר לשנייה בריבוע.
כדי לתאר את הגרף באופן כמותי מלא, נמצא את מהירות הסירה ברגע t=230s.
נשתמש בפונקציית המהירות בתלות בזמן, עבור 80 השניות האחרונות:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1875«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»80«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mrow»«/mstyle»«/math»
נתאר את הגרף:
ובשמונים השניות האחרונות לתנועתה , נעה הסירה בתאוצה קבועה שגודלה 0.1875- מטר לשנייה בריבוע.
נמצא את מהירות הסירה ברגע t=230s , בעזרת פונקציית מהירות בתלות בזמן:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1875«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mrow»«/mstyle»«/math»
נתאר את הגרף:
לאחר מכן נע הסירה בתאוצה שלילית שגודלה 0.1875- מטר לשנייה בריבוע.
כדי לתאר את הגרף באופן מלא , נמצא את מהירות הסירה ברגע t=230s.
נתייחס לתנועת הסירה בשמונים השניות האחרונות , נשתמש בפונקציית מהירות בתלות בזמן:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1875«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»80«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mrow»«/mstyle»«/math»
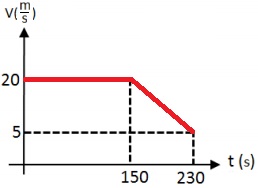
بشكل عام ، يجب إضافة قيم مهمة إلى الرسم البياني. في هذه الحالة ، كان من المهم معرفة سرعة القارب "ب" في اللحظة t= 230s.
______________________________________________________________________________________





![]()