الحلول والمنتديات لـ"ألبوم الحلول" – الكينماتيكا في خط مستقيم
| الموقع: | YouCube |
| المقرر: | קינמטיקה בקו ישר - ערבית |
| كتاب: | الحلول والمنتديات لـ"ألبوم الحلول" – الكينماتيكا في خط مستقيم |
| طبع بواسطة: | משתמש אורח |
| التاريخ: | الأربعاء، 4 فبراير 2026، 12:47 AM |
جدول المحتويات
- 1. 2023,1 - سطح مائل، رسم بياني V(t)
- 2. 2019,1- رمي عمودي ، معطى رسم بياني y(t)
- 3. 2018,1 - ثلاث حركات عمودية
- 4. 2015,1- مخططات مسجل الزمن
- 5. 2013,1- الرسم البياني للموقع كدالة للزمن
- 6. 2013,3- جسم متسارع سؤال بارامتري
- 7. 2012,1- جدول للموقع كدالة للزمن
- 8. 2011,1-مخطط مسجل الزمن
- 9. 2009,1-جسمان تم رميهما نحو الأعلى
- 10. 2008,1-رسم بياني للسرعة كدالة للزمن لجسمين
- 11. 2006,1- رسمان بيانيان للسرعة كدالة للزمن لجسمين متحركين
- 12. 2003,1- رمي جسمين عموديًا ، مع فارق بالزمن
- 13. 2002,1- حركة جسمين في حركة أفقية
- 14. 2001,1- جسمان يتحركان في حركة باليستية
- 15. 2000,1- جسمان يتحركان في حركة باليستية
- 16. 1999,1- جدول للمكان كدالة للزمن
- 17. 1998,1- جدول, ورسم بياني للسرعة كدالة للزمن
- 18. 1996,1-الرسم البياني للسرعة كدالة للزمن
- 19. 1995.1- جدول ورسم بياني للموقع كدالة للزمن
- 20. 1994,1- حركة البالستية - المنطاد
- 21. 1992,1- رسم بياني للسرعة كدالة للزمن لحركة مصعد
- 22. 1988,1-الرسم البياني للسرعة كدالة للزمن ، خط المستقيم
- 23. 1984,17- الرسم البياني للسرعة كدالة للزمن، الخط المستقيم
1. 2023,1 - سطح مائل، رسم بياني V(t)


______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________


______________________________________________________________________________________

______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
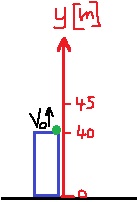
2. 2019,1- رمي عمودي ، معطى رسم بياني y(t)
______________________________________________________________________________________

______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
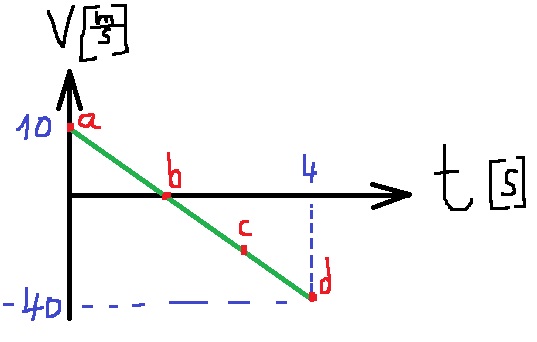
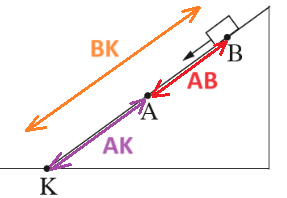
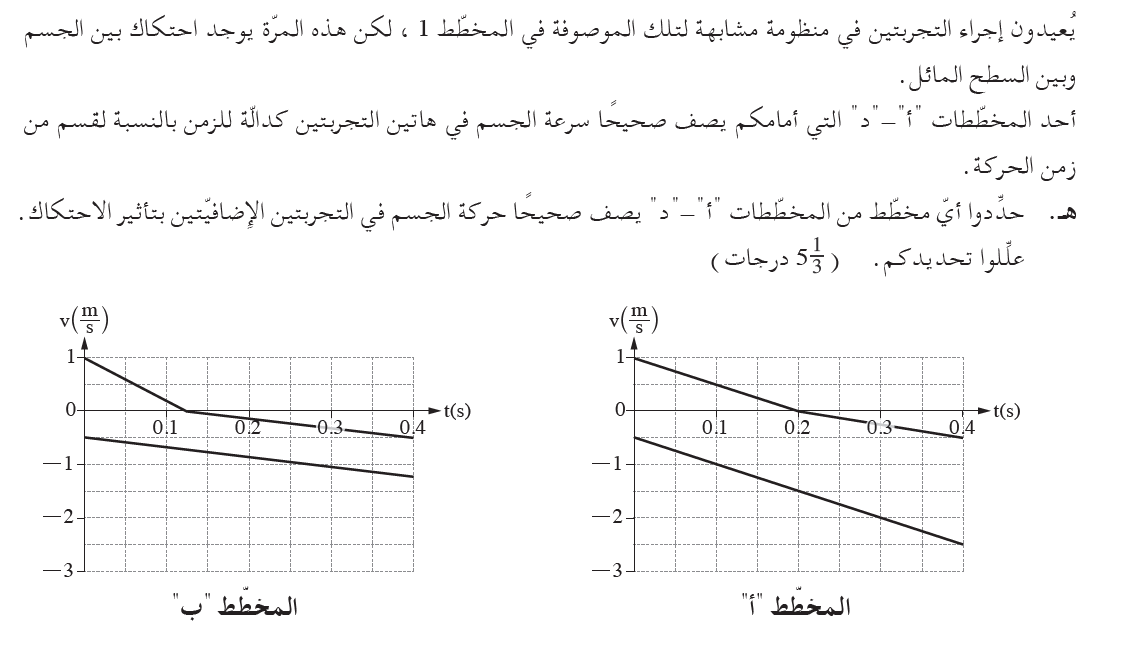
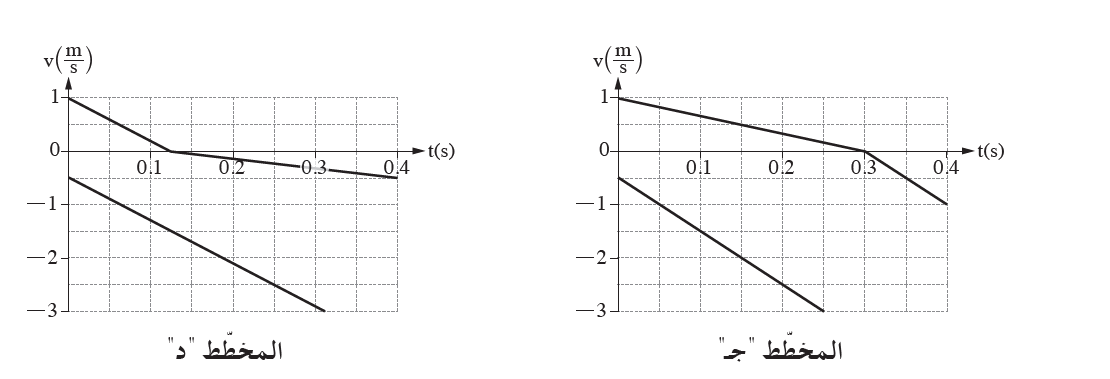
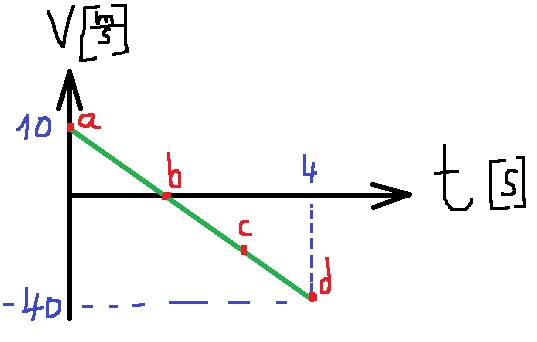
نصف حركة الكرة كدالة للزمن في رسم بياني للسرعة كدالة للزمن. ونشير للنقاط: a, b, c, d .

______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
3. 2018,1 - ثلاث حركات عمودية

______________________________________________________________________________________
في اللحظة التي تبدأ فيها الحركة ، تكون سرعة الكرة الموصوفة في الرسم البياني سالبة ، لأن محور الحركة لأسفل ، وبالتالي فإن الرسم البياني يتوافق مع وصف حركة الكرة التي تم رميها لأعلى. الكرة B.
______________________________________________________________________________________
 ______________________________________________________________________________________
______________________________________________________________________________________
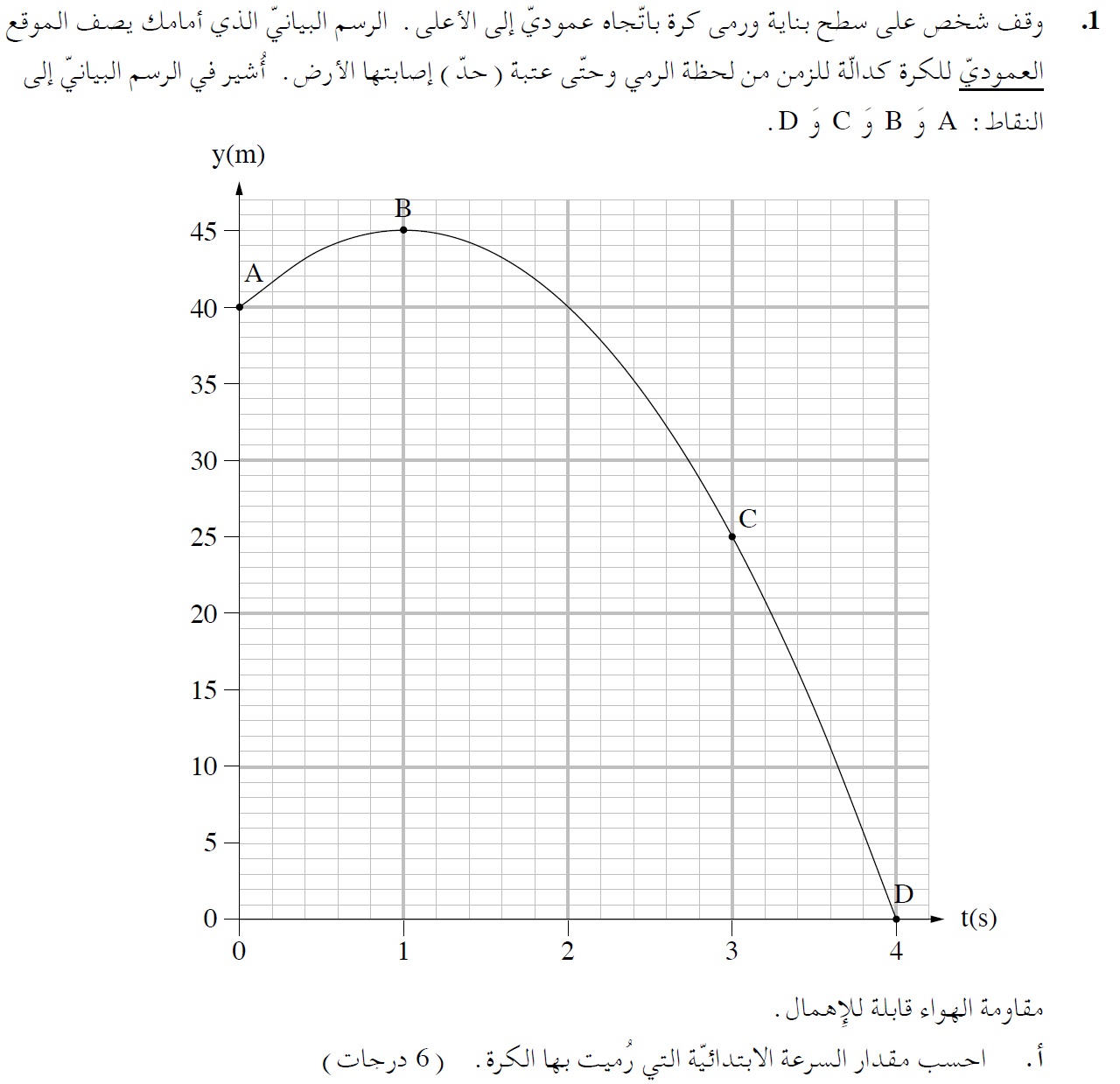
قيمة الموقع النهائي بالنسبة لمحور الحركة هذا تساوي ارتفاع المبنى.
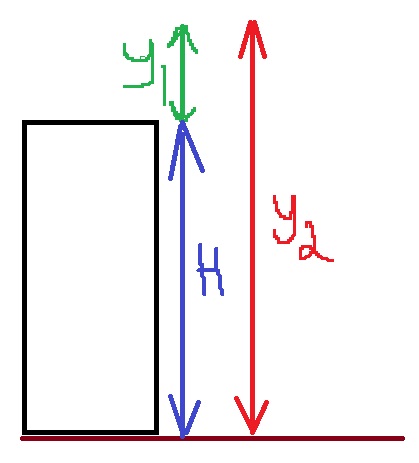

______________________________________________________________________________________
______________________________________________________________________________________
تُرمى الكرة A في اتجاه المحور وتُرمى الكرة B في اتجاه المحور ، وبالتالي فإن السرعة الابتدائية للكرة A تساوي V0 ، وتبلغ سرعة الكرة B هي VO-
نكتب دالة الموقع كدالة للزمن لكل من الكرتين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»Y«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»+«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«mrow»«msub»«mi mathvariant=¨bold¨»Y«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»+«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mrow»«/mstyle»«/math»
نُعرّف دالة جديدة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»y«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mstyle»«/math», التي تصف البعد بين الكرتين في كدالة للزمن:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»y«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»Y«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»Y«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mrow mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»y«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»Y«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»Y«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«/mstyle»«/math»
نجد بمساعدة هذه الدالة البعد بين الكرات في اللحظة t=2s:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/mstyle»«/math»
طريقة إضافية: يمكنك إيجاد موقع كل من الكرتين في اللحظة t = 2s ، وطرح الموقعين لإيجاد البعد بين الكرتين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»Y«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»+«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»2«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»30«/mn»«mi mathvariant=¨bold¨»m«/mi»«mspace linebreak=¨newline¨»«/mspace»«mrow»«msub»«mi mathvariant=¨bold¨»Y«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»+«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»2«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»=«/mo»«/mrow»«mn mathvariant=¨bold¨»10«/mn»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»YA«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»YB«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/mstyle»«/math»
______________________________________________________________________________________

______________________________________________________________________________________
1. ميل الرسم البياني للسرعة كدالة للزمن، يساوي التسارع.
في هذه الحالة ، تتحرك الأجسام الثلاثة تحت تأثير الجاذبية فقط ، وبالتالي فإن تسارعها متساوية ومقدارها g.
2. نقطة التقاطع مع محور السرعة تمثل السرعة الابتدائية ، وهي في هذه الحالة سرعة الرمي.
كل كرة لها سرعة ابتدائية مختلفة.
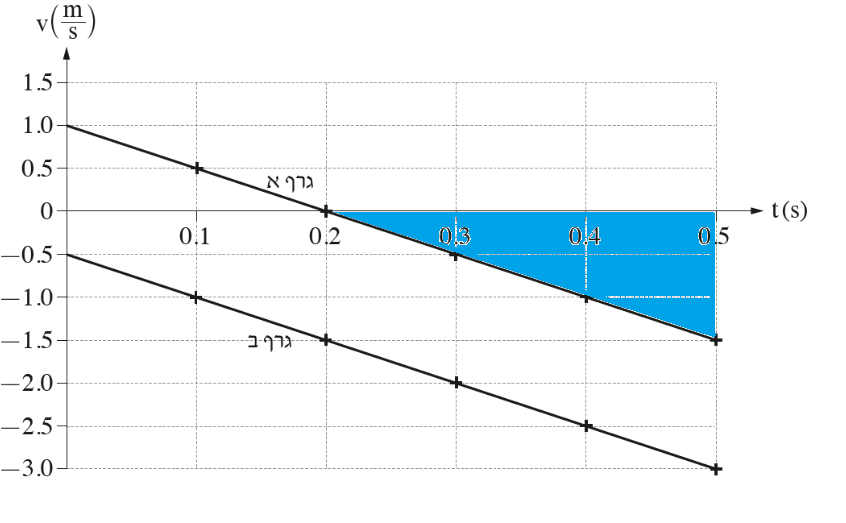
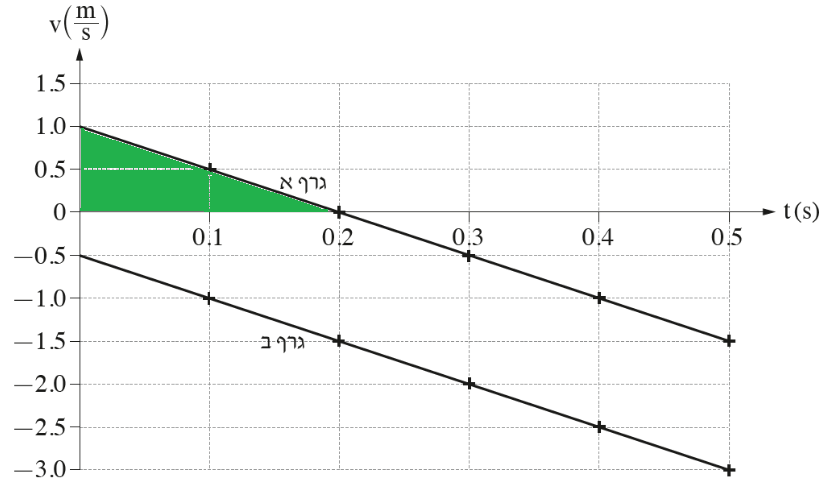
3. المساحة المحصورة تحت الرسم البياني للسرعة كدالة للزمن هي الازاحة.
إذا تطرقنا إلى الازاحة الكلية للكرة B ، فإن الكرات الثلاث لها نفس الازاحة. هذه الازاحة المتساوية تساوي ارتفاع المبنى.
1. في الرسم البياني للسرعة كدالة للزمن، فإن ميل الرسم البياني يساوي التسارع.
في هذه الحالة ، تتحرك الأجسام الثلاثة تحت تأثير الجاذبية فقط ، وبالتالي فإن تسارعها هو نفسه ومقدارها g.
2. معنى نقطة التقاطع مع محور السرعة هي السرعة الابتدائية ، وهي في هذه الحالة سرعة الرمي. كل كرة لها سرعة ابتدائية مختلفة.
3. معنى المساحة المحصورة في الرسم البياني للسرعة كدالة للزمن هي الازاحة.
إذا أشرنا إلى الازاحة الكلية للكرة B ، فإن الكرات الثلاث لها ازاحة متساوية. هذه الازاحة المتساوية تساوي ارتفاع المبنى.
___________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
4. 2015,1- مخططات مسجل الزمن

______________________________________________________________________________________
نحسب متوسط سرعة الشاحنة B ، باستخدام تعريف متوسط السرعة بوحدات متر في الثانية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨top¨»«menclose notation=¨top¨»«mi mathvariant=¨bold¨»V«/mi»«/menclose»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1603;§#1604;§#1610;«/mi»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1603;§#1604;§#1610;«/mi»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»180«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»000«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»3600«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»180«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»000«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»800«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»16«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»66«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mstyle»«/math»
نحسب متوسط سرعة الشاحنة B بوحدات كم / ساعة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨top¨»«menclose notation=¨top¨»«mi mathvariant=¨bold¨»V«/mi»«/menclose»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1603;§#1604;§#1610;«/mi»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1603;§#1604;§#1610;«/mi»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»180«/mn»«mi mathvariant=¨bold-italic¨»k«/mi»«mi mathvariant=¨bold-italic¨»m«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mi mathvariant=¨bold-italic¨»h«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»60«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»km«/mi»«mi mathvariant=¨bold¨»h«/mi»«/mfrac»«/mstyle»«/math»
______________________________________________________________________________________

______________________________________________________________________________________
الإزاحة الكلية للشاحنتين متساوية. لكن زمن حركة الشاحنة A أصغر، من تعريف متوسط السرعة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨top¨»«menclose notation=¨top¨»«mi mathvariant=¨bold¨»V«/mi»«/menclose»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1603;§#1604;§#1610;«/mi»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1603;§#1604;§#1610;«/mi»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/mstyle»«/math»
متوسط سرعة الشاحنة A أكبر.
______________________________________________________________________________________

______________________________________________________________________________________
تتحرك الشاحنة B لمدة 3 ساعات ، في الرسم التخطيطي لحركة الشاحنة B توجد ستة فروق زمنية ، وبالتالي فإن كل فارق زمني مدته نصف ساعة.
الفروق الزمنية في الرسم التخطيطي للشاحنة B متساوية للفروق الزمنية في الرسم التخطيطي للشاحنة A ، وبالتالي فإن كل فارق زمني في حركة الشاحنة A مدته نصف ساعة.
في النصف الأول من حركة الشاحنة A ، يوجد فرقان زمنيان ، وبالتالي فإن زمن حركة الشاحنة A هو ساعة واحدة.
إزاحة الحركة في النصف الأول للحركة الأولى تساوي نصف الإزاحة الكلية وبالتالي هذه الإزاحة تساوي 90 كم.
نحسب مقدار متوسط السرعة بوحدات كم / ساعة في النصف الأول من الحركة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨top¨»«menclose notation=¨top¨»«mi mathvariant=¨bold¨»V«/mi»«/menclose»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1603;§#1604;§#1610;«/mi»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1603;§#1604;§#1610;«/mi»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»90«/mn»«mi mathvariant=¨bold¨»km«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»h«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»90«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»km«/mi»«mi mathvariant=¨bold¨»h«/mi»«/mfrac»«/mstyle»«/math»
______________________________________________________________________________________

______________________________________________________________________________________
في النصف الثاني من حركة الشاحنة A ، توجد ثلاث فروق زمنية ، كل فارق زمني مدته نصف ساعة. لذلك ، فإن زمن حركة الشاحنة A في النصف الثاني من الحركة هو 1.5 ساعة.
نصف إزاحة الحركة الثانية تساوي نصف الإزاحة الكلية، وبالتالي فهي تساوي 90 كم.
نحسب متوسط سرعة الشاحنة A في النصف الثاني من الحركة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨top¨»«menclose notation=¨top¨»«mi mathvariant=¨bold¨»V«/mi»«/menclose»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1603;§#1604;§#1610;«/mi»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1603;§#1604;§#1610;«/mi»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»90«/mn»«mi mathvariant=¨bold-italic¨»k«/mi»«mi mathvariant=¨bold-italic¨»m«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mi mathvariant=¨bold-italic¨»h«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»60«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»km«/mi»«mi mathvariant=¨bold¨»h«/mi»«/mfrac»«/mstyle»«/math»
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
5. 2013,1- الرسم البياني للموقع كدالة للزمن
______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
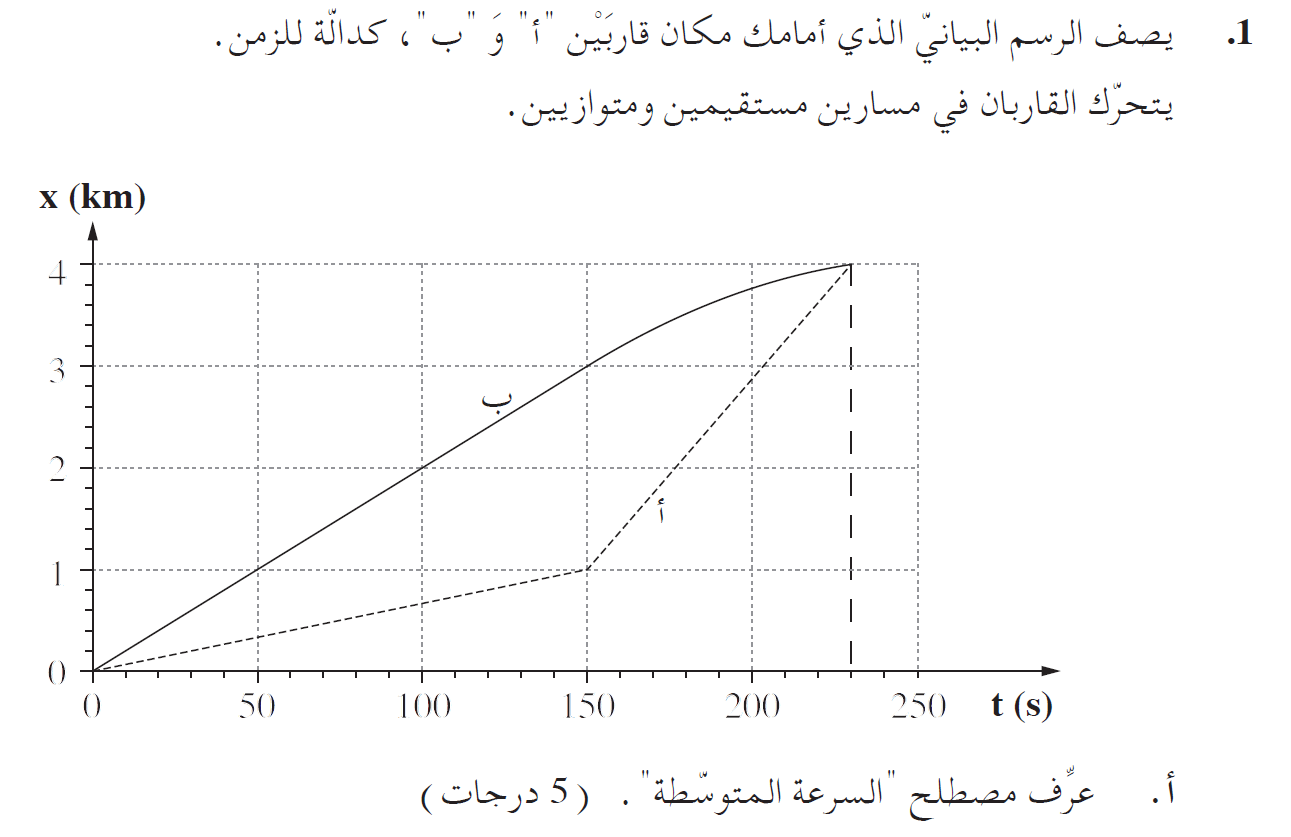
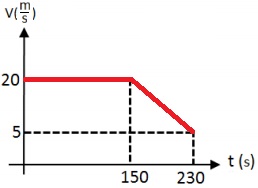
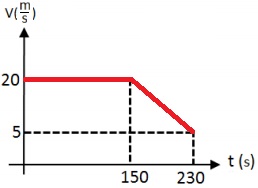
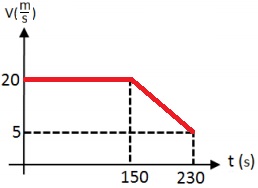
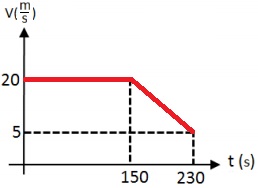
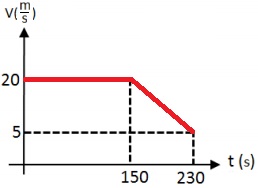
نتطرق إلى حركة القارب "ب" من اللحظة t = 150s حتى اللحظة t = 230s ، من خلال الرسم البياني يمكن ملاحظة أن الإزاحة هي 1000 متر ، وزمن الحركة 80 ثانية.
حتى اللحظة t = 150 ثانية ، يتحرك القارب بسرعة ثابتة. هذه السرعة هي السرعة التي بدأ بها القارب حركته المتسارعة. نحسب هذه السرعة من ميل الرسم البياني في أول 150 ثانية.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»v«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»3000«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»150«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»3000«/mn»«mn mathvariant=¨bold¨»150«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
نكتب معطيات الحركة المتسارعة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»v«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1000«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»80«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»?«/mo»«/math»
يمكنك إيجاد التسارع باستخدام دالة الموقع كدالة للزمن في الحركة المتسارعة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»v«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/math»
نعبّر عن التسارع:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathcolor=¨#0000FF¨»x«/mi»«mo mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mi mathcolor=¨#0000FF¨»x«/mi»«mn»0«/mn»«/msub»«mo mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mi mathcolor=¨#0000FF¨»v«/mi»«mn»0«/mn»«/msub»«mo mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathcolor=¨#0000FF¨»t«/mi»«mo mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn»1«/mn»«mn»2«/mn»«/mfrac»«mo mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathcolor=¨#0000FF¨»a«/mi»«mo mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathcolor=¨#0000FF¨»t«/mi»«mn»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«mo mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathcolor=¨#0000FF¨»x«/mi»«mo mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mi mathcolor=¨#0000FF¨»v«/mi»«mn»0«/mn»«/msub»«mo mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathcolor=¨#0000FF¨»t«/mi»«mo mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn»1«/mn»«mn»2«/mn»«/mfrac»«mo mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathcolor=¨#0000FF¨»a«/mi»«mo mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathcolor=¨#0000FF¨»t«/mi»«mn»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»(«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»v«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«msup»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
نعوّض معطيات الحركة في تعبير التسارع التي حصلنا عليها ، ونجد التسارع :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»(«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»v«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«msup»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»1000«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»80«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«msup»«mn mathvariant=¨bold¨»80«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1200«/mn»«/mrow»«mn mathvariant=¨bold¨»6400«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1875«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
______________________________________________________________________________________

![]()
______________________________________________________________________________________
______________________________________________________________________________________
6. 2013,3- جسم متسارع سؤال بارامتري

______________________________________________________________________________________
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/mrow»«/mstyle»«/math»
نظرًا لأنه مطلوب تطوير تعبيرلمربع السرعة الابتدائية ، نستخدم التعبير لمربع السرعات:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
نعوّض معطيات الحركة ونعبر عن مربع السرعة الأولية كدالة لمسافة الكبح.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«mspace linebreak=¨newline¨»«/mspace»«msup mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«mspace linebreak=¨newline¨»«/mspace»«msup mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

*هذا القسم يبحث في موضوع الطاقة. لا يمكن الإجابة عليه باستخدام مبادئ الكينماتيكا وحدها.

*هذا القسم يبحث في موضوع الديناميكا. لا يمكن الإجابة عليه باستخدام مبادئ الكينماتيكا وحدها.
7. 2012,1- جدول للموقع كدالة للزمن
______________________________________________________________________________________
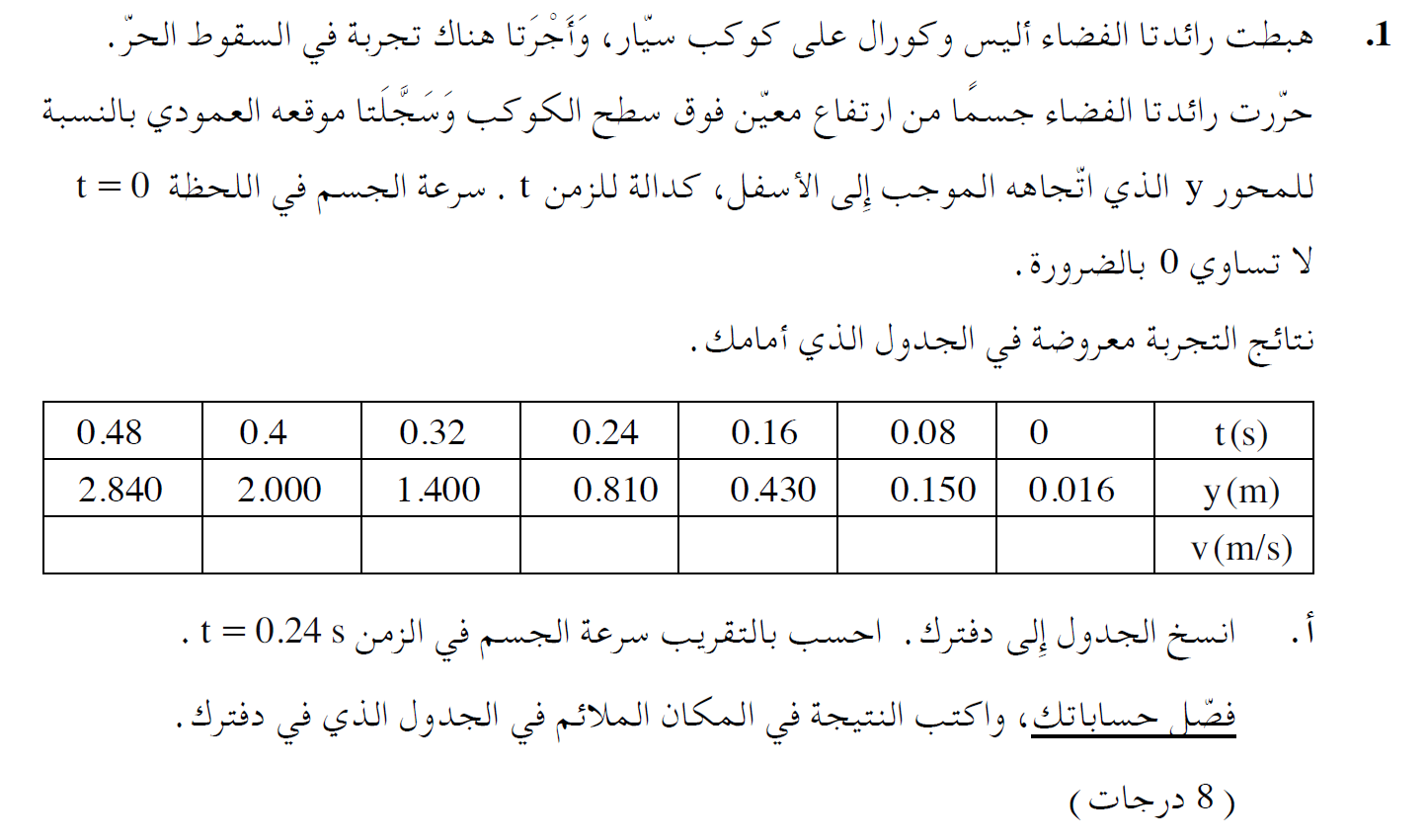
متوسط السرعة في فترة زمنية معينة لجسم يتحرك بتسارع ثابت يساوي تمامًا السرعة اللحظية في منتصف تلك الفترة الزمنية. لذلك ، نحسب متوسط السرعة من اللحظة t = 0.16s حتى اللحظة t = 0.32s .
نجد إزاحة من هذه الحركة باستخدام المعطيات الموجودة في الجدول:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»16«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«menclose mathcolor=¨#0000FF¨ notation=¨top¨»«mi mathvariant=¨bold¨»V«/mi»«/menclose»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»16«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»32«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1603;§#1604;§#1610;«/mi»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»Y«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»16«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»32«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1603;§#1604;§#1610;«/mi»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»16«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»32«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»43«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»32«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»16«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»97«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»16«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»06«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
______________________________________________________________________________________

______________________________________________________________________________________

إن تسارع الأجسام على سطح كل كوكب سيار ثابت. وعندما يتحرك جسم بتسارع ثابت ، فإن متوسط سرعة الجسم في مقطع حركة معين يساوي السرعة اللحظية في منتصف زمن جزء الحركة هذا.
نحسب السرعات اللحظية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»08«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«menclose mathcolor=¨#0000FF¨ notation=¨top¨»«mi mathvariant=¨bold¨»V«/mi»«/menclose»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»016«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1603;§#1604;§#1610;«/mi»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»y«/mi»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»016«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1603;§#1604;§#1610;«/mi»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»016«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»43«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»016«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»16«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»97«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»16«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»58«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»16«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«menclose mathcolor=¨#0000FF¨ notation=¨top¨»«mi mathvariant=¨bold¨»V«/mi»«/menclose»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»08«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»24«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1603;§#1604;§#1610;«/mi»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»y«/mi»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»08«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»24«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1603;§#1604;§#1610;«/mi»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»08«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»24«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»81«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»15«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»24«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»08«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»66«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»16«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»32«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«menclose mathcolor=¨#0000FF¨ notation=¨top¨»«mi mathvariant=¨bold¨»V«/mi»«/menclose»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»24«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1603;§#1604;§#1610;«/mi»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»y«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»24«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1603;§#1604;§#1610;«/mi»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»24«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»81«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»24«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»16«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»43«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«menclose mathcolor=¨#0000FF¨ notation=¨top¨»«mi mathvariant=¨bold¨»V«/mi»«/menclose»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»32«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»48«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1603;§#1604;§#1610;«/mi»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»y«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»32«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»48«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1603;§#1604;§#1610;«/mi»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»32«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»48«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»84«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»48«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»32«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»44«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»16«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

______________________________________________________________________________________

______________________________________________________________________________________


______________________________________________________________________________________
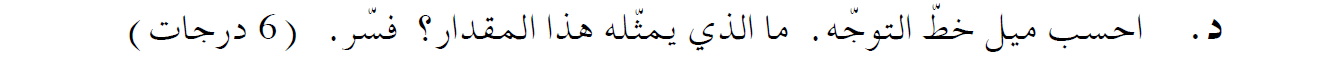
______________________________________________________________________________________
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold-italic¨»V«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»58«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»08«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»42«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»32«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
______________________________________________________________________________________

* لا يمكن الإجابة على هذا القسم باستخدام الكينماتيكا وحده. يبحث هذا القسم مع الجاذبية.
8. 2011,1-مخطط مسجل الزمن
______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
نتطرق إلى مقطع الحركة بين نقطة قبل النقطة A ونقطة بعد النقطة A. ونجد متوسط السرعة في مقطع الحركة هذا.
زمن الحركة الكلي في مقطع الحركة هذا: 0.04 ثانية.
الإزاحة الكلية (كما تلاحظ في الرسم البياني) هي 2.8 سم أي 0.028 متر.
نحسب متوسط السرعة في مقطع الحركة هذه:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨top¨»«mi mathvariant=¨bold¨»V«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»028«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»04«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
______________________________________________________________________________________

______________________________________________________________________________________
لإيجاد تسارع العربة ، نجد سرعة العربة في أزمنة مختلفة ، ونبني رسمًا بيانيًا للسرعة كدالة للزمن ، نظرًا لأن التسارع ثابت ، يجب أن يكون ميل الرسم البياني ثابتًا ويساوي تسارع العربة.
نتطرق إلى النقطة الأولى التي تم الإشارة لها على أنها النقطة رقم 1 ، وإلى النقطة الثانية على أنها النقطة رقم 2 ، وما إلى ذلك. نجد السرعة في لحظة طباعة النقاط 2 ، 4 ، 6 ، 7. (يمكنك اختيار نقاط أخرى)
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»012«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»04«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»02«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»04«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»028«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»04«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»032«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»04«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
نتطرق إلى لحظة طباعة النقطة الثانية على أنها صفر ، وزمن طباعة النقاط الأخرى وفقًا لذلك.
سوف نحصل على
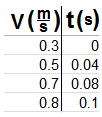
وفقًا لذلك ، نرسم رسمًا بيانيًا للسرعة كدالة للزمن ، وسوف نحصل على:
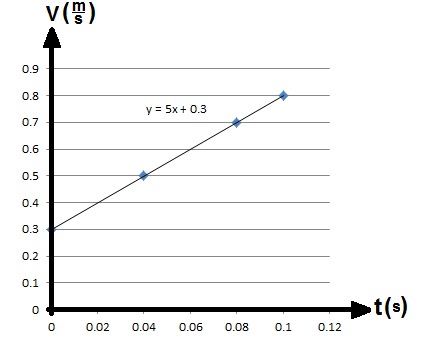
لإيجاد التسارع ، نحسب ميل الرسم البياني بواسطة نقطتان تقعان على الرسم البياني :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«mrow mathcolor=¨#0000FF¨/»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»v«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
لذلك تتحرك العربة بتسارع ثابت مقداره 5 أمتار لكل ثانية مربعة.
______________________________________________________________________________________

______________________________________________________________________________________
لا تظهر النقطة P (النقطة التاسعة) في الرسم التخطيطي ، لكننا نعلم أنه حتى في لحظة طباعة النقطة P ، تتحرك العربة بتسارع 5 أمتار لكل ثانية مربعة. تمت طباعة النقطة بعد 0.04 ثانية من طباعة النقطة السابعة.
نتطرق إلى حركة العربة من لحظة طباعة النقطة السابعة حتى لحظة طباعة النقطة التاسعة (الحركة بتسارع ثابت) ، نكتب معطيات الحركة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»7«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»04«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«mspace linebreak=¨newline¨/»«/math»
يمكن استخدام هذه المعطيات في دالة الموقع كدالة للزمن للحركة بتسارع ثابت ، حتى نجد الإزاحة التي قطعها الجسم من لحظة طباعة النقطة السابعة حتى لحظة طباعة النقطة التاسعة.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»v«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»v«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»04«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«msup mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»04«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»032«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»004«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»036«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
البعد بين النقطة السابعة والتاسعة 0.036 متر. من الشكل يمكن ملاحظة أن البعد بين النقطة السابعة والنقطة الثامنة هو 0.017 متر.
نحسب البعد بين النقطة الثامنة والنقطة التاسعة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«mrow»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»,«/mo»«mi mathvariant=¨bold¨»P«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«mrow»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«mrow»«mn mathvariant=¨bold¨»7«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«mrow»«mn mathvariant=¨bold¨»7«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»036«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»017«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»019«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cm«/mi»«/math»
______________________________________________________________________________________
9. 2009,1-جسمان تم رميهما نحو الأعلى
* هذا السؤال يختلف عن السؤال الأصلي ، وتم ملائمته مع موضوع الكينماتيكا في خط مستقيم.
 ______________________________________________________________________________________
______________________________________________________________________________________
نصف حركة الكرتين نسبة لمحور الحركة Y الموجهة لأعلى ، ونقطة أصله بسطح الأرض.
نُشير للكرة A على أنها الكرة رقم 1 ، والكرة B بالرقم 2. وسنكتب معطيات حركة الكرتين نسبة لمحور الحركة الذي تم اختياره.
سرعة كل من الكرتين آخذه بالنقصان لذا تتحرك كل منهما بتسارع سالب.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathcolor=¨#0000FF¨»Y«/mi»«msub»«mn»0«/mn»«mn»1«/mn»«/msub»«/msub»«mo mathcolor=¨#0000FF¨»=«/mo»«mn mathcolor=¨#0000FF¨»45«/mn»«mi mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«msub mathcolor=¨#0000FF¨»«mi mathcolor=¨#0000FF¨»V«/mi»«msub»«mn»0«/mn»«mn»1«/mn»«/msub»«/msub»«mo mathcolor=¨#0000FF¨»=«/mo»«mn mathcolor=¨#0000FF¨»40«/mn»«mfrac mathcolor=¨#0000FF¨»«mi»m«/mi»«mi»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«msub mathcolor=¨#0000FF¨»«mi mathcolor=¨#0000FF¨»a«/mi»«mn»1«/mn»«/msub»«mo mathcolor=¨#0000FF¨»=«/mo»«mi mathcolor=¨#0000FF¨»g«/mi»«mo mathcolor=¨#0000FF¨»=«/mo»«mo mathcolor=¨#0000FF¨»-«/mo»«mn mathcolor=¨#0000FF¨»10«/mn»«mfrac mathcolor=¨#0000FF¨»«mi»m«/mi»«msup»«mi»s«/mi»«mn»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathcolor=¨#0000FF¨»Y«/mi»«mn»02«/mn»«/msub»«mo mathcolor=¨#0000FF¨»=«/mo»«mn mathcolor=¨#0000FF¨»0«/mn»«mi mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«msub mathcolor=¨#0000FF¨»«mi mathcolor=¨#0000FF¨»V«/mi»«mn»02«/mn»«/msub»«mo mathcolor=¨#0000FF¨»=«/mo»«mn mathcolor=¨#0000FF¨»55«/mn»«mfrac mathcolor=¨#0000FF¨»«mi»m«/mi»«mi»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«msub mathcolor=¨#0000FF¨»«mi mathcolor=¨#0000FF¨»a«/mi»«mn»2«/mn»«/msub»«mo mathcolor=¨#0000FF¨»=«/mo»«mi mathcolor=¨#0000FF¨»g«/mi»«mo mathcolor=¨#0000FF¨»=«/mo»«mo mathcolor=¨#0000FF¨»-«/mo»«mn mathcolor=¨#0000FF¨»10«/mn»«mfrac mathcolor=¨#0000FF¨»«mi»m«/mi»«msup»«mi»s«/mi»«mn»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«/math»
بدأت الكرتان تحركان من نفس اللحظة، وزمن حركة الكرتان هو نفسه في أي لحظة ، نكتب دالة الموقع كدالة للزمن لكل من الكرتين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Y«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»45«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Y«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»55«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«/math»
نجد لحظة الإلتقاء - في لحظة الإلتقاء، يكون موقع الكرات هو نفسه ، لذلك لإيجاد لحظة الإلتقاء ، نقارن موقع الكرتين:-
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mtext mathcolor=¨#0000FF¨»55t-«/mtext»«mfrac mathcolor=¨#0000FF¨»«mn»1«/mn»«mn»2«/mn»«/mfrac»«mo mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathcolor=¨#0000FF¨»10«/mn»«mo mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathcolor=¨#0000FF¨»t«/mi»«mn»2«/mn»«/msup»«mo mathcolor=¨#0000FF¨»=«/mo»«mn mathcolor=¨#0000FF¨»45«/mn»«mo mathcolor=¨#0000FF¨»+«/mo»«mn mathcolor=¨#0000FF¨»40«/mn»«mi mathcolor=¨#0000FF¨»t«/mi»«mo mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mn»1«/mn»«mn»2«/mn»«/mfrac»«mo mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathcolor=¨#0000FF¨»10«/mn»«mo mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathcolor=¨#0000FF¨»t«/mi»«mn»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«mn mathcolor=¨#0000FF¨»15«/mn»«mi mathcolor=¨#0000FF¨»t«/mi»«mo mathcolor=¨#0000FF¨»=«/mo»«mn mathcolor=¨#0000FF¨»45«/mn»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«mspace linebreak=¨newline¨/»«/math»
نجد موقع الإلتقاء - نعوّض لحظة الإلتقاء في إحدى دالتي الموقع كدالة للزمن: -
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Y«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»55«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Y«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»55«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»165«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»45«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»120«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«/math»
لذا تلتقي الكرتان بالموقع y = 120m ، أي على ارتفاع 120 مترًا فوق سطح الأرض.
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
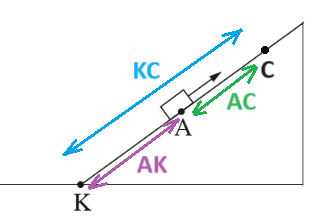
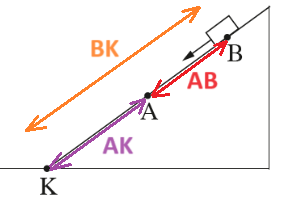
عندما يكون مقدار سرعة كل من الكرتين متساوٍ، يتحقق «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/mrow»«/mstyle»«/math»
نكتب دالة السرعة كدالة للزمن لكل من الكرتين. ونقارن بين الدالتين.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»55«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»55«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»55«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»95«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»75«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
لذلك ، فإن سرعة كل من الكرتين تكون متساوية المقدار بعد مرور 4.75 ثانية من رميهما.
إذا عوّضنا هذه اللحظة في التعبير لسرعة أحدى الكرتين كدالة للزمن، فسنجد أنه في في هذه اللحظة t = 4.75 ثانية ، تتحرك الكرة B لأعلى في اتجاه محور المكان بسرعة 7.5 متر لكل الثانية ، والكرة A تتحرك لأسفل بسرعة 7.5- متر في الثانية.
______________________________________________________________________________________
10. 2008,1-رسم بياني للسرعة كدالة للزمن لجسمين

 _____
_____
نحسب ميل الرسم البياني:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»30«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mrow»«/mstyle»«/math»
زادت سرعة الدراجة النارية لمدة 15 ثانية بمقدار 30 مترًا في الثانية.
______________________________________________________________________________________

____________________________________________________________________________________
في التمثيل البياني للسرعة كدالة زمنية ، يكون ميل الرسم البياني مساويًا لتسارع الجسم. نجد ميل الرسم البياني في الفترة الزمنية بين t = 5s t = 15s.
بكلمات أخرى ، نستخدم تعريف التسارع:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»v«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»25«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»25«/mn»«/mrow»«mn mathvariant=¨bold¨»10«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
______________________________________________________________________________________

______________________________________________________________________________________
الموقع الابتدائي للدراجة النارية هو X0=30m. والموقع الابتدائي للسيارة هو X0 = 0m .
في الرسم البياني للسرعة كدالة للزمن ، فإن المساحة المحصورة بين الرسم البياني ومحور الزمن تساوي إزاحة الجسم.
نجد إزاحة كل مركبة بمساعدة الرسم البياني، نُشير للسيارة على أنها الجسم 1 ، والدراجة النارية كجسم 2:
نحسب إزاحة السيارة حسب المساحة المحصورة تحت الرسم البياني الذي يصف حركة السيارة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»25«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»125«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»125«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»250«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
نحسب إزاحة الدراجة النارية حسب المساحة المحصورة تحت الرسم البياني الذي يصف حركة الدراجة النارية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»30«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»225«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
نجد موقع كل من السيارتين في اللحظة t = 15s:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«msub»«mn mathvariant=¨bold¨»0«/mn»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»250«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»250«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«msub»«mn mathvariant=¨bold¨»0«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»225«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»255«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/mrow»«/mstyle»«/math»
إزاحة الدراجة النارية أصغر من إزاحة السيارة ، ولكن بسبب المواقع البدائية في اللحظة t = 15 ثانية ، تسبق الدراجة النارية السيارة.
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
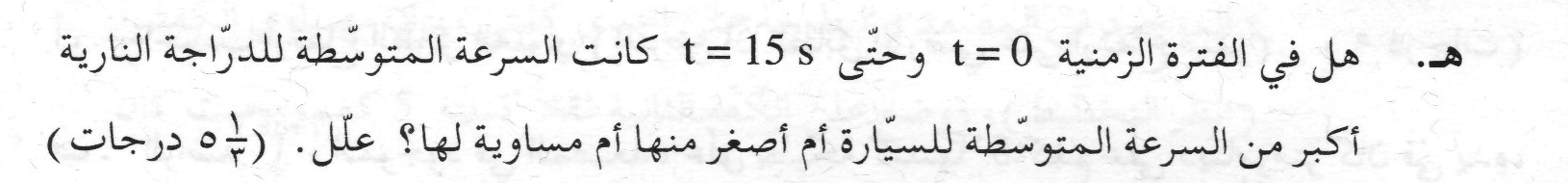
______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
من خلال الرسم البياني يمكن أن نرى أن سرعة السيارتين متساوية عندما تتحرك السيارة بتسارع سالب.
نظرًا لأن التسارع ثابت ، يمكن أن نستخدم دالة السرعة كدالة للزمن لوصف سرعة كل واحدة من المركبتين .
نُشير للدراجة النارية بالجسم رقم 1, نكتب الدالة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»v«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mstyle»«/math» الملائمة لوصف حركة الدراجة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mrow mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»v«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mspace linebreak=¨newline¨/»«mrow mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»v«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
نُشير للسيارة بالجسم رقم 2, نكتب الدالة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»v«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mstyle»«/math» الملائمة لوصف حركة السيارة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mrow mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»v«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»02«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mspace linebreak=¨newline¨/»«mrow mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»v«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
نكتب معادلة الأزمنة التي تربط t1 بـ t2. في لحظة الإلتقاء ، يكون زمن تسارع السيارة أقل بخمس ثوانٍ من زمن تسارع الدراجة النارية ، لذلك:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»5«/mn»«/menclose»«/mstyle»«/math»
في اللحظة التي تتساوى فيها سرعة المركبتين يتحقق: V1 =V2. نقارن بين دالتي السرعة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mrow mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»v«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»v«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»25«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/menclose»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
نحل هيئة المعادلات. ونجد t1 و- t2:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»15«/mn»«mspace linebreak=¨newline¨/»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»333«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
نُعوّض t2 , ونجد t1.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mspace linebreak=¨newline¨/»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«/mstyle»«/math»
وبالتالي ، فإن سرعت المركبتين تكون متساوية بعد 8.33 ثانية من بدء حركة الدراجة النارية.
undefined
נציב את t2 ,ונמצא את t1.
undefined
לכן מהירויות כלי הרכב זהות כעבור 8.33 שניות מרגע תחילת תנועת האופנוע.
______________________________________________________________________________________
11. 2006,1- رسمان بيانيان للسرعة كدالة للزمن لجسمين متحركين
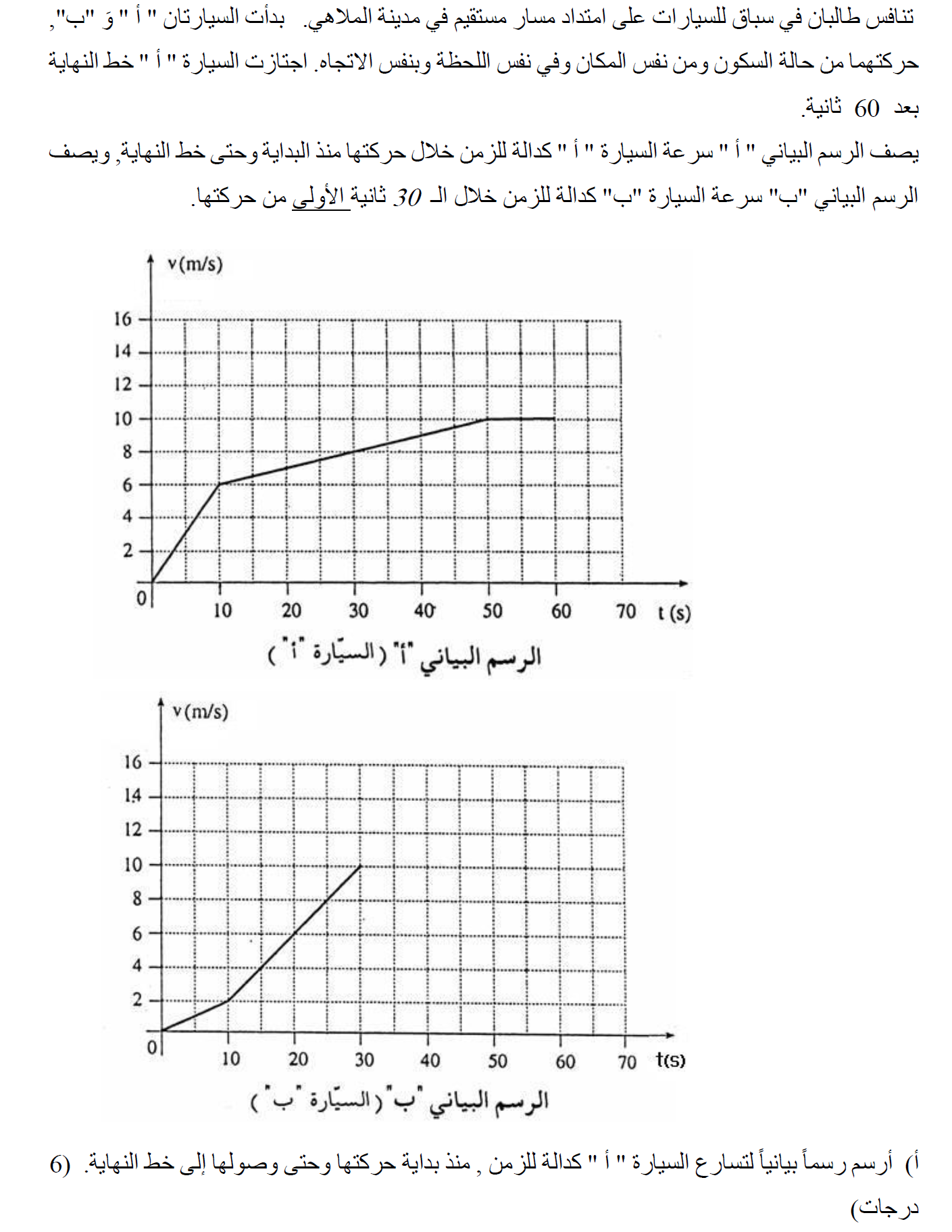
______________________________________________________________________________________
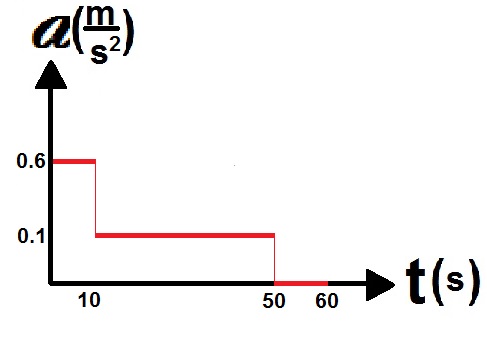
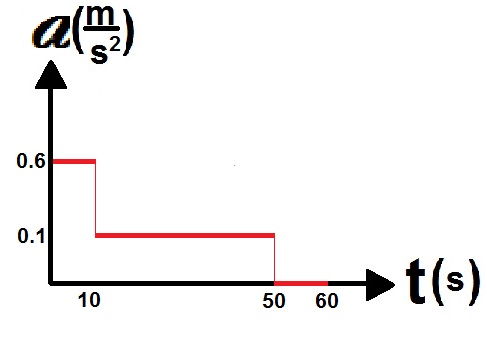
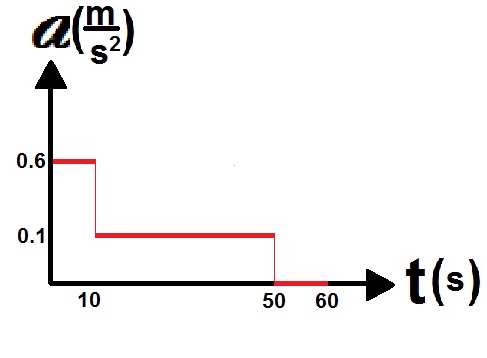
______________________________________________________________________________________

______________________________________________________________________________________
الطريقة أ: الإزاحة الكلية التي تقطعها السيارة "أ" ، تساوي المساحة المحصورة بين دالة السرعة ومحور الزمن، خلال مدة 60 ثانية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»40«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»320«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»450«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
طريقة ب': يمكن استخدام دالة الموقع كدالة للزمن الملائمة لتسارع ثابت لإيجاد الإزاحة في كل من الحركات الثلاثة.
المسافة التي قطعتها السيارة من اللحظة التي بدأت فيها التحرك حتى وصلت إلى خط النهاية تساوي مجموع هذه الإزاحات الثلاث.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»140«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»320«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1499;§#1493;§#1500;§#1500;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»320«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»450«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«/mrow»«/mstyle»«/math»
لذلك ، فإن البعد بين نقطة بداية الحركة ونقطة النهاية ، التي تتحرك على طولها السيارة "أ" ، تساوي 450 مترًا.
______________________________________________________________________________________

______________________________________________________________________________________
نحسب المساحة المحصورة بين الرسم البياني "أ"، بين دالة السرعة ومحور الزمن في أول 30 ثانية من حركة السيارة "أ":
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»6«/mn»«mi mathvariant=¨bold¨»§#1473;§#1473;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»20«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»140«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»170«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»10«/mn»«mi mathvariant=¨bold¨»§#1473;§#1473;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»20«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»120«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»130«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
نتطرق إلى حركة السيارة "ب" من اللحظة t = 30s ، حتى لحظة وصولها إلى خط النهاية.
- نجد زمن حركة السيارة "ب" في المقطع الأخير من الحركة:
تتحرك السيارة "أ" لمدة 60 ثانية ، وتتحرك السيارة "ب" على طول نفس المسار ووصلت قبل ذلك بثانيتين، وبالتالي الزمن الكلي لحركة السيارة "ب" مساوٍ لـ 58 ثانية. لذلك ، من اللحظة t = 30 ثانية حتى اللحظة التي تَعْبُر فيها السيارة B خط النهاية ( مقطع الحركة الذي نتطرق إليه) فإنها تتحرك لمدة 28 ثانية.
- نجد إزاحة حركة السيارة "ب" في القسم الأخير من الحركة:
في اللحظة t = 30s ، تكون السيارة "ب" في الموقع x = 130m ، وطول المسار كما يبدو من حركة السيارة "أ" هو 450 مترًا ، وبالتالي بدءًا من اللحظة t = 30s حتى لحظة عبور السيارة "ب" خط النهاية تكون إزاحتها 320 مترا.
نكتب معطيات الحركة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»28«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»320«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»?«/mo»«/math»
يمكن استخدام دالة الموقع للزمن المناسبة للحركة بتسارع ثابت، وإيجاد تسارع السيارة "ب" حسب هذه الدالة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«mrow»«mstyle displaystyle=¨true¨»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«/mstyle»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»320«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»28«/mn»«/mrow»«mrow»«mstyle displaystyle=¨true¨»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«/mstyle»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»28«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»40«/mn»«mn mathvariant=¨bold¨»392«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»102«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
______________________________________________________________________________________
12. 2003,1- رمي جسمين عموديًا ، مع فارق بالزمن

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
عند رمي الحجر من سطح الأرض وعودته إلى سطح الأرض ، تكون إزاحة الحجر صفرًا. من التعبير عن مربع السرعات ، مقدار سرعة إصابة الحجر بسطح الأرض مساوية لسرعة القذف، يكون اتجاه حركة الحجر في لحظة إصابته بسطح الأرض عكس اتجاه حركته في لحظة الرمي: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/math»
نستخدم دالة السرعة كدالة للزمن «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«/math», لتطوير تعبير لزمن حركة كل حجر من الحجرين من لحظة الرمي حتى لحظة الاصطدام بسطح الأرض:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»a«/mi»«/mfrac»«/math»
نحسب زمن حركة كل حجر من لحظة الرمي إلى لحظة عودته إلى سطح الأرض :
إذا تم رمي الحجرين معًا في نفس اللحظة ، فإن الحجر الثاني سيصطدم بسطح الأرض بعد 0.4 ثانية ، ولكن بسبب أن الحجر الثاني رُمي بعد 0.5 ثانية من رمي الحجر الأول ، فإن الحجر الثاني سيصطدم بسطح الأرض بعد 0.9 ثانية من اصطدام الحجر الأول .
______________________________________________________________________________________

______________________________________________________________________________________
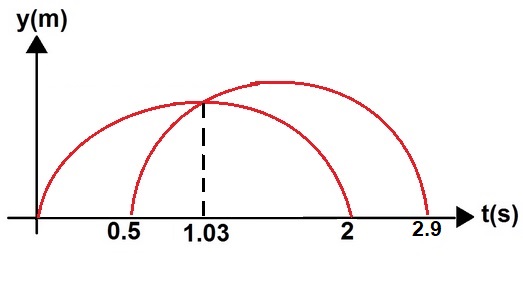
1. إذا ت مرمي الحجر الأول في اللحظة t = 0s ، فإن الحجر الثاني تم رميه في اللحظة t = 0.5s
2. الحجر الأول يصيب الأرض بعد ثانيتين من رميه
3. أصاب الحجر الثاني الأرض بعد 2.4 ثانية من رميه، أي بعد 2.9 ثانية من رمي الحجر الأول.
4. في اللحظة t = 1.03s يكون الحجران على نفس الارتفاع.
5. يتم رمي الحجر الأول بسرعة أكبر ، وبالتالي يصل إلى ارتفاع أكبر.
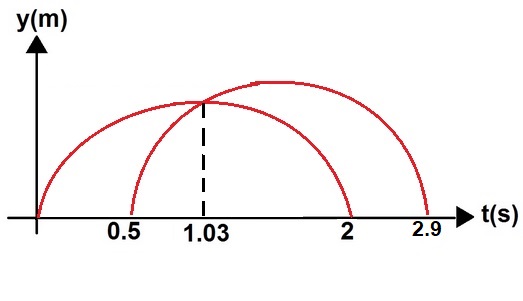
1. אם האבן הראשונה נזרקה ברגע t=0s , האבן השנייה נזרקה ברגע t=0.5s
2.האבן הראשונה פוגעת בקרקע שתי שניות לאחר שנזרקה
3. האבן השנייה פוגעת בקרקע 2.4 שניות לאחר זריקתה, זאת אומרת 2.9 שניות לאחר זריקת אבן הראשונה.
4. ברגע t=1.03s שת י האבנים נמצאות באותו גובה.
5. האבן הראשונה נזרק במהירות גדולה יותר לכן היא מגיעה לגובה גדול יותר.
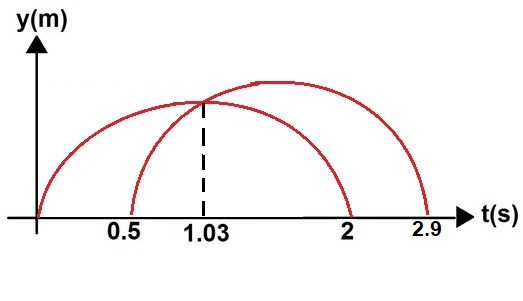
______________________________________________________________________________________
13. 2002,1- حركة جسمين في حركة أفقية

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
تتحرك كلتا المركبتين في نفس الاتجاه، دعنا نفرض إنهما تتحركان إلى اليمين. نختيار محور حركة باتجاه حركة المركبتين نحو اليمين.
نشير لبداية المحور في النقطة التي تتواجد فيها الدراجة النارية في اللحظة t = 0s.
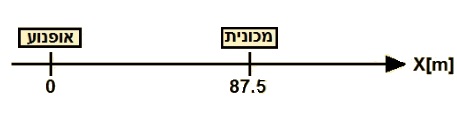
تتحرك السيارة بسرعة 108 كم / ساعة ، وهذه السرعة بالوحدات القياسية تساوي 30 مترًا في الثانية (نقسم على 3.6).
الموقع الإبتدائي للسيارة بالنسبة لمحور الحركة المحدد هو 87.5 مترًا.
نصف موقع السيارة كدالة للزمن، بمساعدة دالة الموقع كدالة للزمن المناسبة للحركة بسرعة ثابتة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mrow»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»87«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»30«/mn»«mi mathvariant=¨bold¨»t«/mi»«/menclose»«/mstyle»«/math»
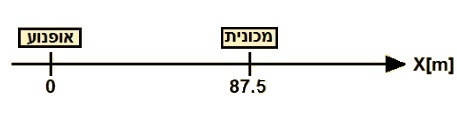
______________________________________________________________________________________

______________________________________________________________________________________
نكتب تعبير الموقع كدالة للزمن المناسب لوصف حركة الدراجة النارية.
بالنسبة إلى المحور المحدد ، فإن الموقع الإبتدائي للدراجة النارية هو 0.
تتحرك الدراجة النارية في اتجاه المحور بسرعة متزايدة ، وتسارعها 2 متر لكل ثانية مربعة.
سنكتب تعبير الموقع كدالة للزمن لحركة الدراجة النارية. بالنسبة للمحور المحدد في القسم ب:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
______________________________________________________________________________________

______________________________________________________________________________________
لمعرفة زمن الإلتقاء، نُشير للدراجة النارية بأنها الجسم 1 ، والسيارة هي الجسم 2. وسنقارن بين دالتي الموقع كدالة للزمن:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»87«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»87«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mspace linebreak=¨newline¨/»«/math»
تم الحصول على معادلة من الدرجة الثانية، سنقوم بترتيب المعادلة وإيجاد حلول لها:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»87«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»30«/mn»«mo mathvariant=¨bold¨»§#177;«/mo»«msqrt»«mo mathvariant=¨bold¨»(«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»30«/mn»«msup»«mo mathvariant=¨bold¨»)«/mo»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»(«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»87«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»)«/mo»«/msqrt»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»30«/mn»«mo mathvariant=¨bold¨»§#177;«/mo»«mn mathvariant=¨bold¨»40«/mn»«/mrow»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»70«/mn»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»17«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«mspace linebreak=¨newline¨/»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«mspace linebreak=¨newline¨/»«/math»
الزمن السالب ليس له أي معنى فيزيائي، وبالتالي فإن الدراجة النارية ستلحق بالسيارة بعد مرور 17.5 ثانية.
______________________________________________________________________________________

______________________________________________________________________________________
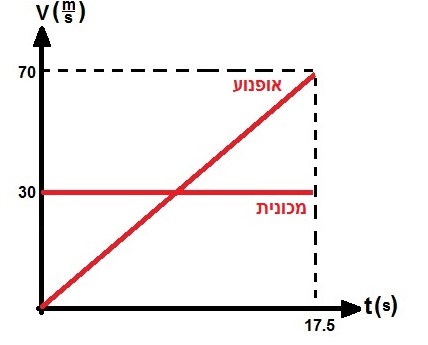
نحسب سرعة الدراجة النارية باستخدام دالة السرعة كدالة للزمن:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»17«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»70«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«/mrow»«/mstyle»«/math»
لذلك ، في لحظة الإلتقاء t = 17.5 ثانية ، تكون سرعة الدراجة النارية 70 مترًا في الثانية.
سرعة السيارة ثابتة ومقدارها 30 مترا في الثانية.
نصف حركة الدراجة النارية والسيارة في رسم بياني للسرعة كدالة للزمن:
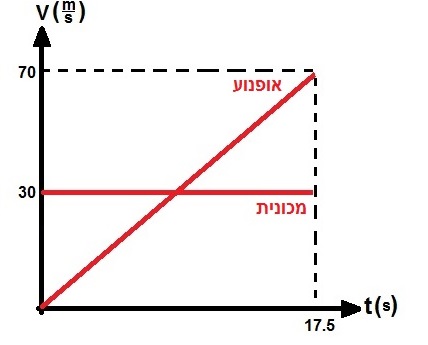
______________________________________________________________________________________
14. 2001,1- جسمان يتحركان في حركة باليستية

______________________________________________________________________________________
نختار محور حركة يبدأ من نقطة رمي الكرتين (عند ارتفاع سقف المبنى) ويتجه نحو الأسفل.
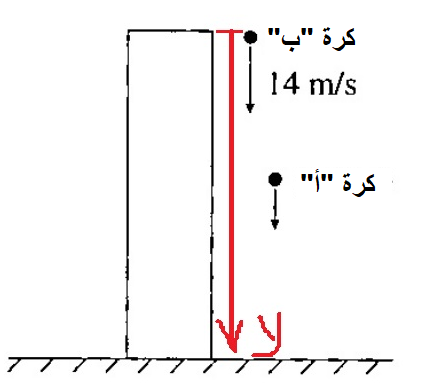
بالنسبة إلى هذا المحور، تكون سرعة الكرتين دائمًا موجبة وتتزايد.
نكتب معطيات حركة الكرة "أ" نسبة لمحور الحركة الذي تم اختياره:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Y«/mi»«msub»«mn mathvariant=¨bold¨»0«/mn»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«msub»«mn mathvariant=¨bold¨»0«/mn»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨/»«/math»
نستخدم دالة الموقع كدالة للزمن المناسبة لوصف حركة جسم يتحرك بتسارع ثابت:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»y«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»y«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«/math»
___________________________________________________________________________________
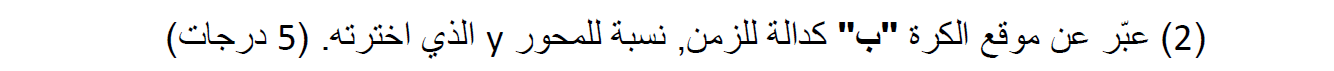
______________________________________________________________________________________
undefined
undefined
نكتب معطيات حركة الكرة "ب" ، بالنسبة إلى محور الحركة المحدد.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«msub»«mn mathvariant=¨bold¨»0«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«msub»«mn mathvariant=¨bold¨»0«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»14«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/mrow»«/mstyle»«/math»
وفقًا لذلك، نكتب التعبير الخاص بموقع الكرة 2 كدالة للزمن:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Y«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»Y«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»14«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«/mrow»«/mstyle»«/math»
______________________________________________________________________________________

______________________________________________________________________________________
نقارن بين دالتي الموقع كدالة للزمن للكرتين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mn mathvariant=¨bold¨»14«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«/mstyle»«/math»
يتم تحرير الكرة "أ" ثانية واحدة بعد رمي الكرة "ب". لذلك ، فإن زمن حركة الكرة "أ" أكبر بمقدار ثانية واحدة من زمن حركة الكرة "ب".
نكتب معادلة الزمن :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»1«/mn»«/menclose»«/mstyle»«/math»
لإيجاد t1 ، عبّر عن t2 من معادلة الزمن الثانية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathcolor=¨#0000FF¨»§#8658;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«/menclose»«/mstyle»«/math»
نعوّض التعبير t2 في المعادلة المرة لأولى:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»14«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»14«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfenced mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mfenced mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»14«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»14«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mfenced mathcolor=¨#0000FF¨»«mrow»«msup»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»14«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»14«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»9«/mn»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«/mstyle»«/math»
لذلك ، بعد 2.25 ثانية من لحظة إطلاق الكرة A. الكرتان تلتقيان.
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«/mstyle»«/math»
يتم تحرير الكرة "أ" ثانية واحدة بعد رمي الكرة "ب". لذلك ، فإن زمن حركة الكرة "أ" أكبر بمقدار ثانية واحدة من زمن حركة الكرة "ب".
نكتب معادلة الزمن الإضافي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»1«/mn»«/menclose»«/mstyle»«/math»
لإيجاد t1 ، نُعبّر عن t2 من معادلة الزمن الإضافية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathcolor=¨#0000FF¨»§#8658;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«/menclose»«/mstyle»«/math»
نعوّض التعبير t2 أعلاه في المعادلة الأولى:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfenced mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mfenced mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mfenced mathcolor=¨#0000FF¨»«mrow»«msup»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/mstyle»«/math»
لقد حصلنا على معادلة بدون حل ، ولا توجد قيمة لـ t تحقق المعادلة ، وبالتالي لا توجد أيضًا لحظة تلتقي فيها الكرتان.
נשווה בין פונקציות המקום זמן של שני הכדורים:
undefined
undefined
כדור א' משוחרר שנייה אחת לפי שכדור ב' נזרק. לכן, זמן התנועה של כדור א' גדול בשנייה אחת מזמן התנועה של כדור ב'.
נכתוב את משוואת הזמנים הנוספת:
undefined
כדי למצוא את t1 ,נבטא את t2 ממשוואת הזמנים השנייה :
undefined
נציב את ביטוי t2 במשוואת הזמנים הראשונה:
undefined
קבלנו משוואה ללא פתרון, אין ערך של t המקיים את המשוואה, לכן גם אין רגע בו נפגשים שני הכדורים.
______________________________________________________________________________________
15. 2000,1- جسمان يتحركان في حركة باليستية

______________________________________________________________________________________
نتطرق إلى حركة الكرة "أ" ، من لحظة الرمي إلى لحظة وصولها إلى قمة ارتفاعها. نسبة لمحور الحركة الذي تم اختياره في السؤال.
نكتب معطيات الحركة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»?«/mo»«/math»
يمكن التعبير عن إزاحة الحركة من التعبير لمربع السرعات.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»y«/mi»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/mrow»«/mfrac»«/math»
نعوّض معطيات الحركة ونجد إزاحة الحركة ، هذه الإزاحة تساوي أقصى ارتفاع ستصل إليه الكرة في حركتها.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mn mathvariant=¨bold¨»0«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«msup»«mn mathvariant=¨bold¨»40«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»(«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1600«/mn»«/mrow»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»20«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»80«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
______________________________________________________________________________________

______________________________________________________________________________________
نتطرق إلى حركة الكرة من لحظة رميها لأعلى حتى لحظة إصابتها الأرض (حتى تعود إلى نقطة الرمي). نصف الحركة نسبة لمحور الحركة الوارد في السؤال.
نكتب معطيات الحركة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»?«/mo»«/math»
طريقة "أ" : لإيجاد زمن الحركة ، يمكنك استخدام دالة الموقع كدالة للزمن لحركة بتسارع ثابت.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/math»
نعوّض معطيات الحركة ونجد الزمن t:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»40«/mn»«mn mathvariant=¨bold¨»5«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«mspace linebreak=¨newline¨/»«/math»
لذلك ، فإن الزمن المنقضي من لحظة رمي الكرة إلى لحظة اصابتها الأرض هو 8 ثوانٍ.
طريقة "ب": من تعبير مربع السرعات عندما تكون الإزاحة مساوية للصفر ، فإن السرعة النهائية تساوي في المقدار السرعة الابتدائية. لذلك ، هذه السرعات متساوية لكن مع الإشارات المعاكسة (اتجاهات الحركة المعاكسة).
لذلك يمكن القول أنه في هذه الحركة يتحقق : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/math»
نستخدم دالة السرعة كدالة للزمن , «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«/math» نعبر عن زمن الحركة ونستخدم العلاقة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/math».
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»40«/mn»«/mrow»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«/math»
للتلخيص: الكرة تتحرك بتسارع الجاذبية، كل ثانية تقل سرعتها بمقدار 10 أمتار في الثانية، وسرعتها البدائية 40 مترًا في الثانية ، وبالتالي بعد 4 ثوانٍ تصبح سرعة الكرة صفرًا ، (وتتوقف في نقطة قمة الارتفاع ). وقتزمن الهبوط يساوي زمن الصعود ، الزمن الكلي الذي يمر من لحظة رمي الكرة لأعلى حتى تعود إلى نقطة الرمي هو 8 ثوان.
______________________________________________________________________________________

______________________________________________________________________________________
بدأت الكرتان بالحركة في نفس اللحظة، وكلاهما تتحركان تحت تأثير الجاذبية فقط ، وبالتالي فإن تسارعهما 10 متر لكل ثانية مربعة.
نكتب معطيات الحركة ودالة الموقع كدالة للزمن للكرة "أ"، ونشير للكرة "أ" على أنها الجسم 1:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Y«/mi»«msub»«mn mathvariant=¨bold¨»0«/mn»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«msub»«mn mathvariant=¨bold¨»0«/mn»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Y«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/math»
نكتب معطيات الحركة ودالة الموقع كدالة للزمن للكرة "أ"، ونشير للكرة "ب" على أنها الجسم 2:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Y«/mi»«msub»«mn mathvariant=¨bold¨»0«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»300«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«msub»«mn mathvariant=¨bold¨»0«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Y«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»300«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/math»
نجد زمن الإلتقاء من خلال مقارنة دالتي الموقع كدالة للزمن:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Y«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Y«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»300«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»300«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»60«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»300«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mspace linebreak=¨newline¨/»«/math»
لذلك ، تلتقي الكرتان بعد مرور 5 ثوانٍ من لحظة بدئهما في التحرك.
______________________________________________________________________________________

______________________________________________________________________________________
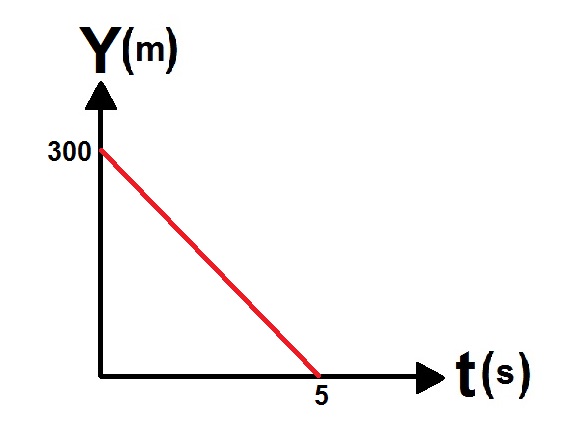
نُعرّف دالة جديدة Y3 تصف البعد بين الكرتين كدالة للزمن:
نُعرّف الدالة الجديدة بدلالة الدالتين : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Y«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/math» ו - «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Y«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»300«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/math»
بحيث أن الدالة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Y«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math» تصف في أي لحظة البعد بين الكرتين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Y«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Y«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Y«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math»
نعوّض الدالتين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Y«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»300«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math»
نُبسّط التعبير:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Y«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»300«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»Y«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»300«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»60«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/menclose»«/math»
نصف الدالة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Y«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math» في الرسم البياني للموقع كدالة للزمن:
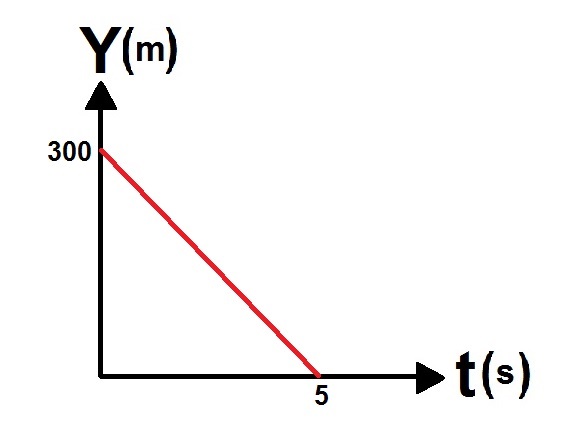
المنطق وراء الرسم البياني - في اللحظة t = 0 البعد بين الكرتين 300 متر. تتغير سرعتا الكرتين بنفس الوتيرة (كلاهما يتحركان مع تسارع الجاذبية) لذلك يكون فرق السرعة بين الكرتين ثابتًا (60 مترًا في الثانية). البعد بين الكرتين يقل خطيًا بمقدار 60 مترًا كل ثانية ،
في البداية كانت المسافة بين الكرتين 300 متر. وبعد 5 ثوانٍ تلتقي الكرتين ويكون البعد بينهما صفرًا.
______________________________________________________________________________________
16. 1999,1- جدول للمكان كدالة للزمن
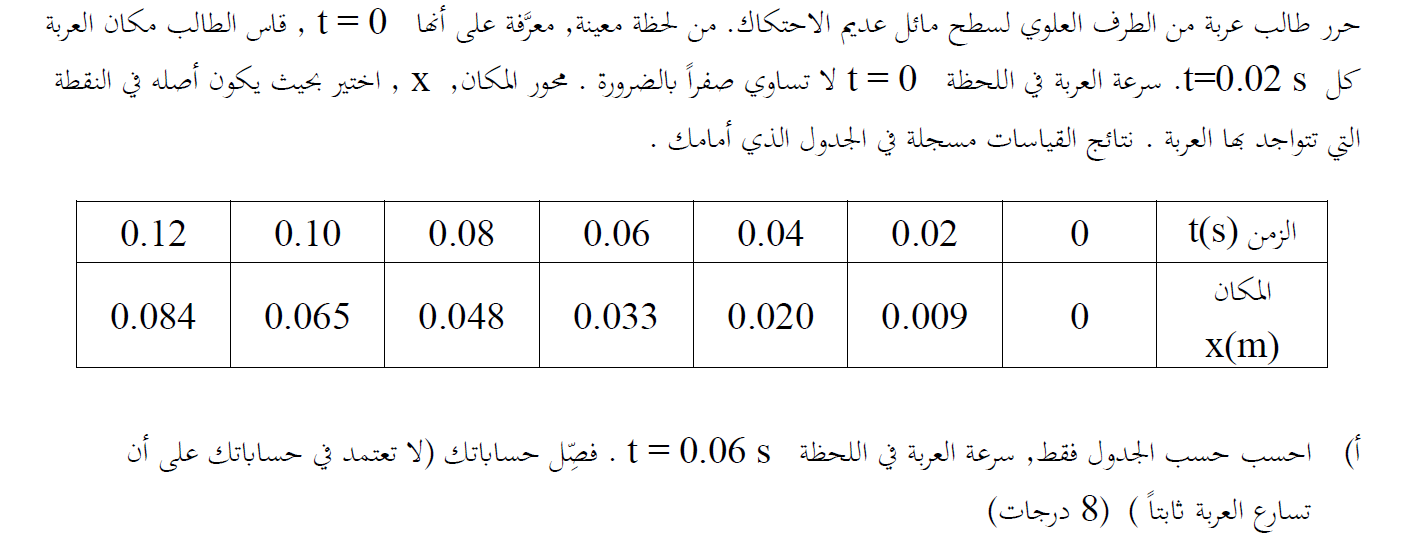
______________________________________________________________________________________
نتطرق إلى الحركة بين اللحظة t = 0.04s واللحظة t = 0.08s ، متوسط السرعة في هذه الحركة يساوي تقريبًا السرعة اللحظية في منتصف الفترة الزمنية هذه أي في اللحظة t = 0.06s.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»06«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨top¨»«mi mathvariant=¨bold¨»V«/mi»«/menclose»«msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»04«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»08«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»x«/mi»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»04«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»08«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»04«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»08«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»048«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»02«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»08«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»04«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»028«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»04«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mstyle»«/math»
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
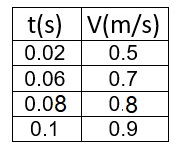
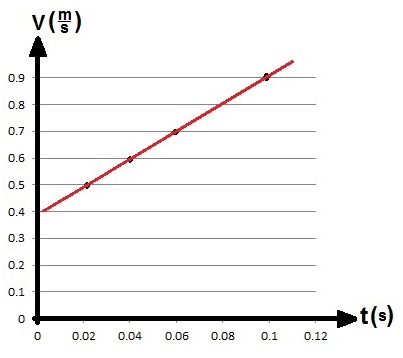
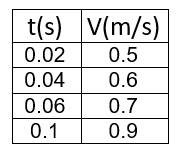

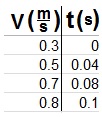
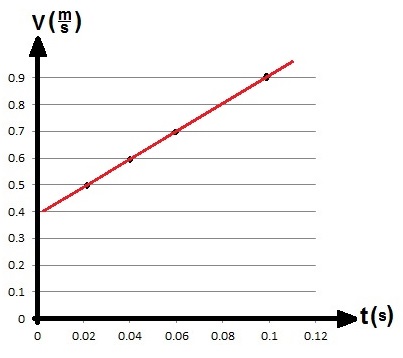
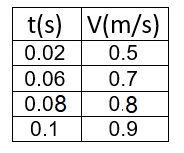
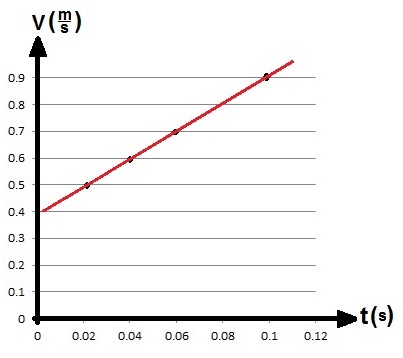
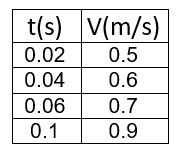

______________________________________________________________________________________
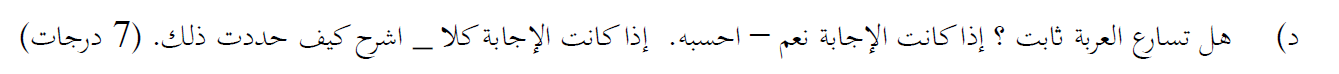
______________________________________________________________________________________
______________________________________________________________________________________
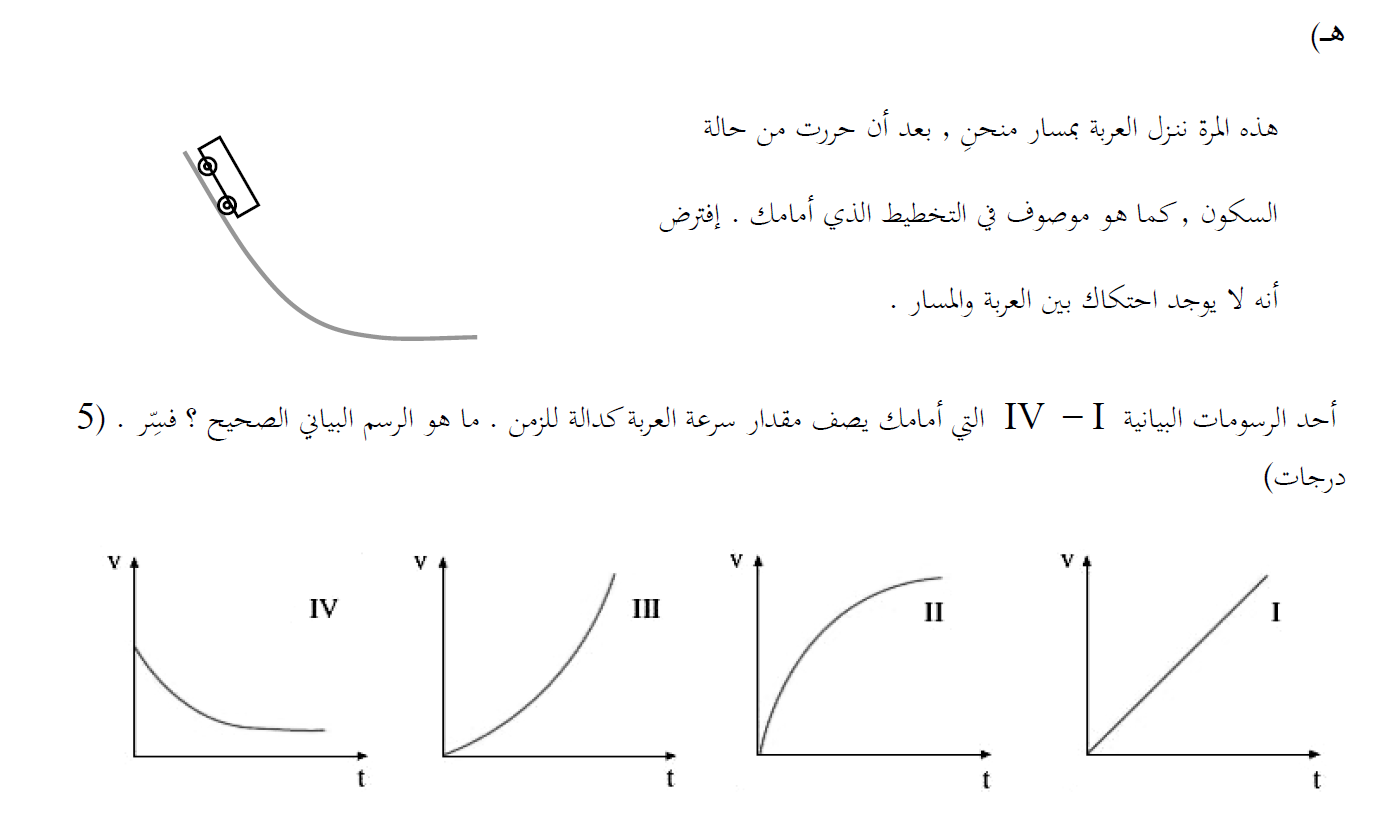
______________________________________________________________________________________
______________________________________________________________________________________
17. 1998,1- جدول, ورسم بياني للسرعة كدالة للزمن
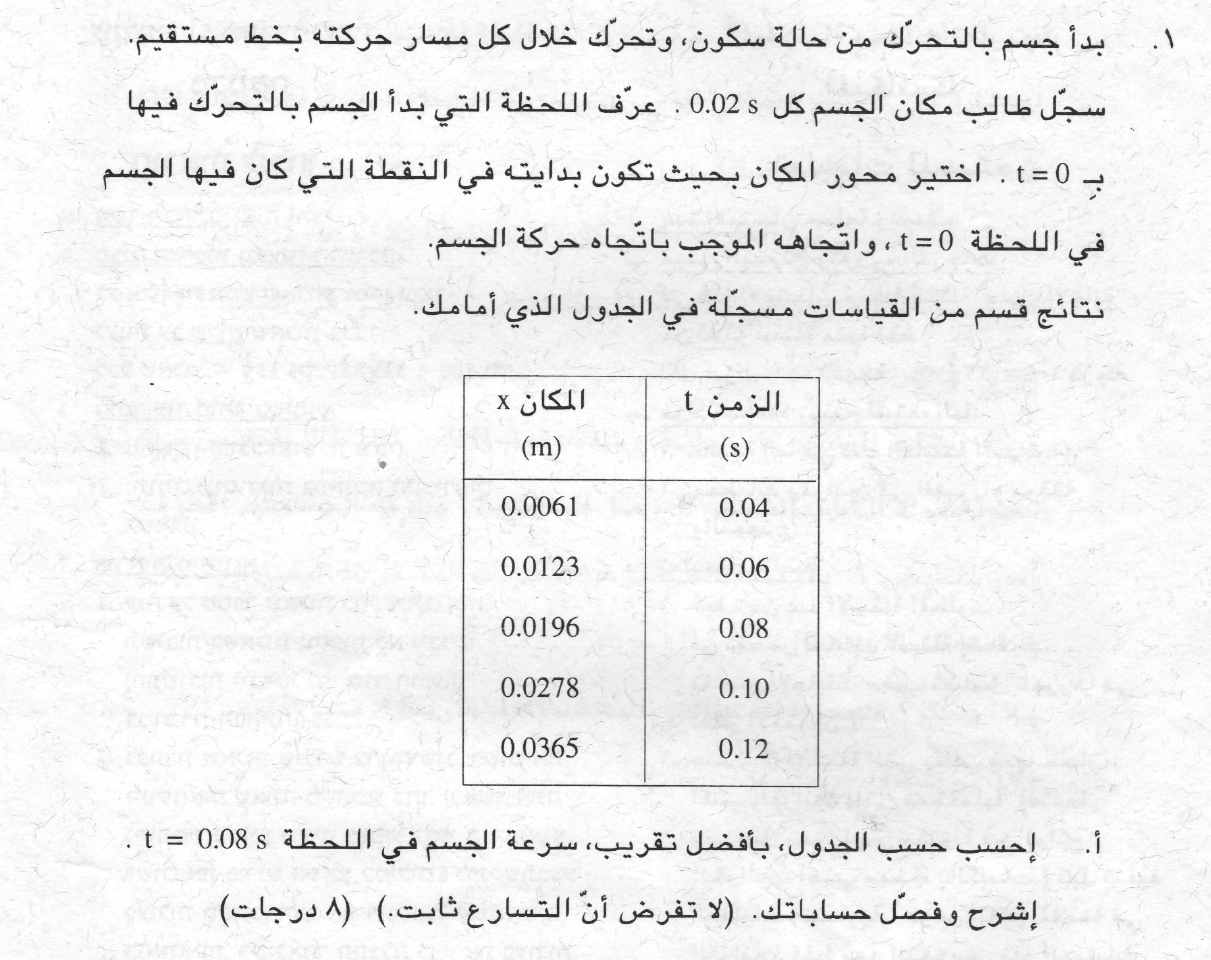
______________________________________________________________________________________
نتطرّق إلى مقطع الحركة بين اللحظة t = 0.06s واللحظة t = 0.1s ، متوسط السرعة في هذه الفترة الزمنية يساوي تقريبًا السرعة اللحظية في منتصف الفترة أي اللحظة t=0.08s.
نحسب متوسط السرعة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨top¨»«mi mathvariant=¨bold¨»V«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#1499;§#1493;§#1500;§#1500;«/mi»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»§#1499;§#1493;§#1500;§#1500;«/mi»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»0278«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»0123«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»06«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»0155«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»04«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3875«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
هذه السرعة تساوي السرعة في منتصف الفترة الزمنية للحركة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»08«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3785«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mstyle»«/math»
______________________________________________________________________________________
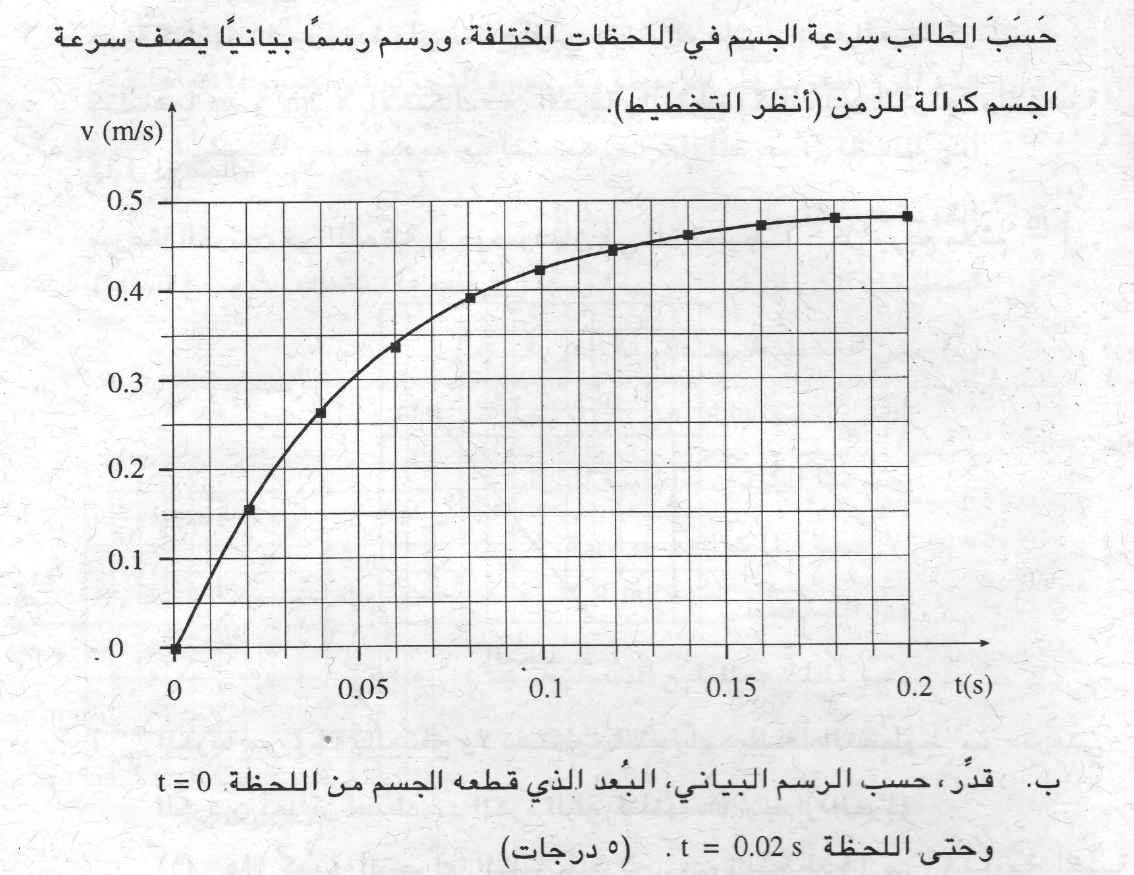
______________________________________________________________________________________
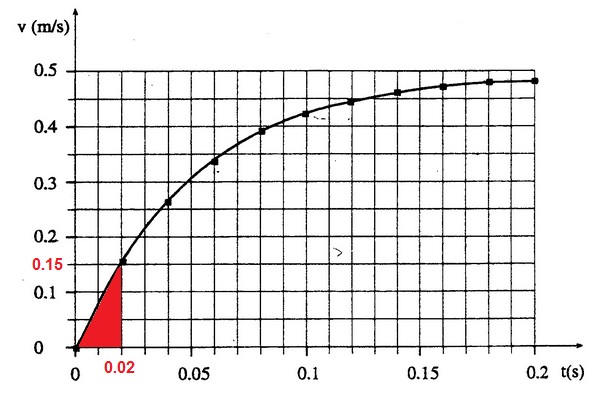

______________________________________________________________________________________

______________________________________________________________________________________
الميل في الرسم البياني للسرعة كدالة للزمن يساوي التسارع، وميل القاطع في للرسم البياني للسرعة كدالة للزمن في فترة زمنية معينة يساوي متوسط التسارع في تلك الفترة الزمنية. في الرسم البياني التالي، ميل الخط القاطع أخضر اللون يساوي متوسط التسارع في أول 0.02 ثانية.
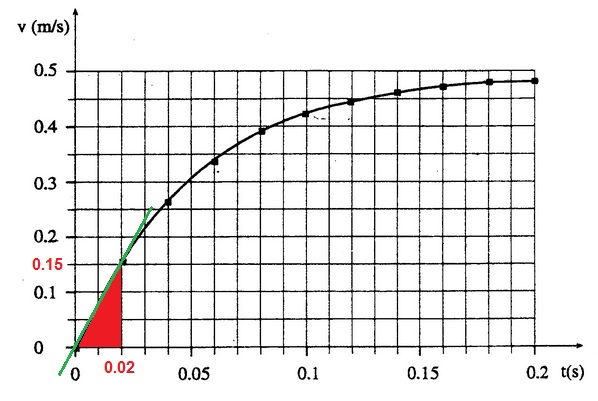
نحسب ميل الخط القاطع (باللون الأخضر) في أول 0.02 ثانية من الحركة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»v«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»v«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»-«/mo»«/mrow»«/msub»«msub»«mi mathvariant=¨bold¨»v«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»02«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
إذن ، متوسط تسارع الجسم هو 7.5 أمتار لكل ثانية مربعة.
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

* يبحث القسمان هـ، و في موضوع الديناميكا، ولا يمكن الإجابة على هذه الأقسام بمساعدة فهم الكينماتيكا وحدها.
18. 1996,1-الرسم البياني للسرعة كدالة للزمن
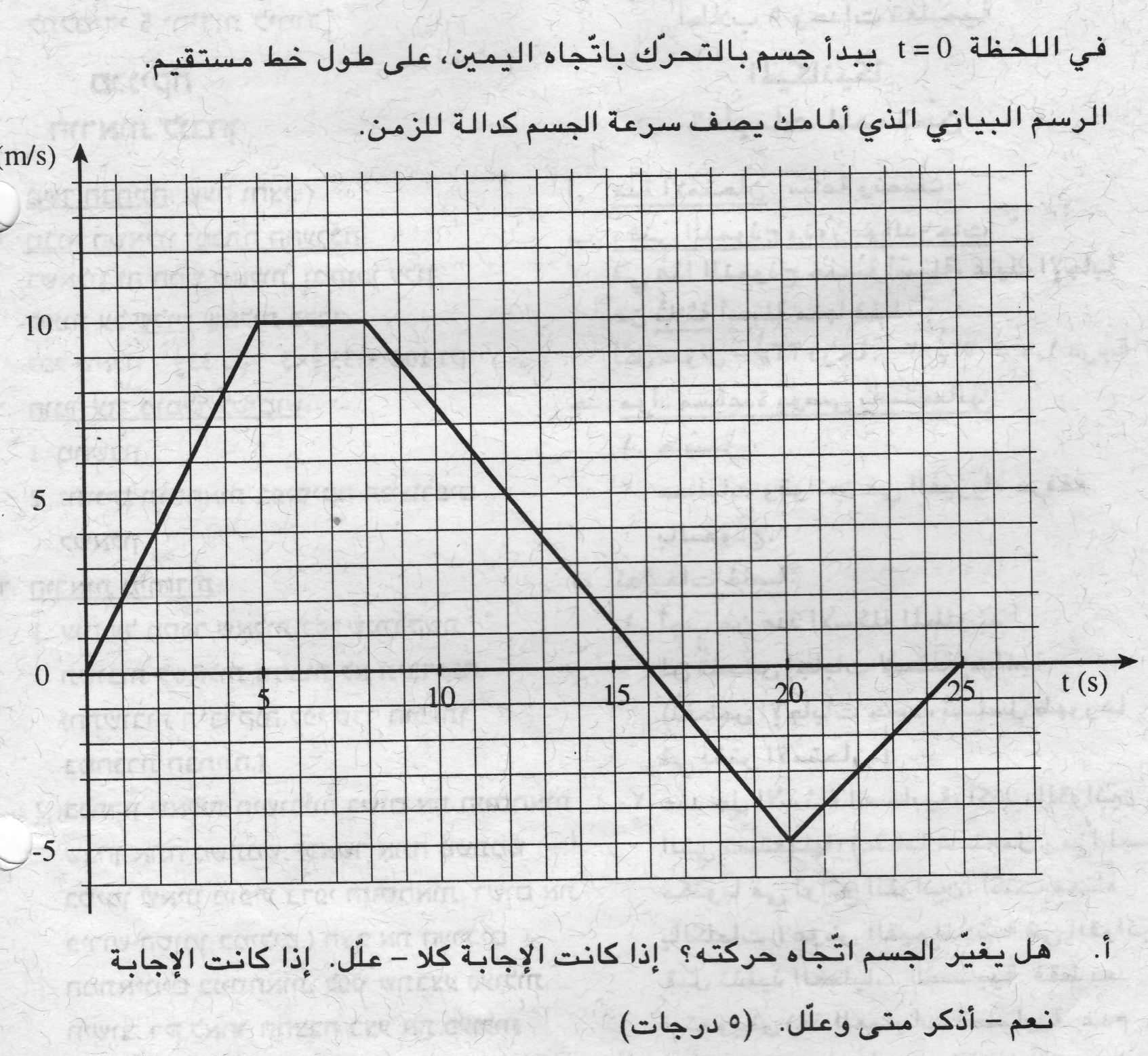
___________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
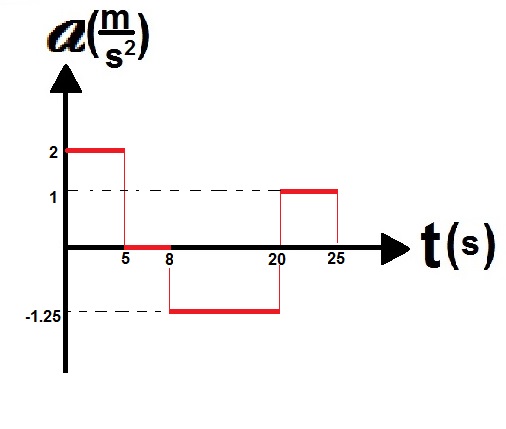
في التمثيل البياني للسرعة كدالة للزمن، يكون ميل الرسم البياني مساويًا لتسارع الجسم.
نحسب ميل الرسم البياني في كل جزء من أجزاء الحركة :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»v«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»v«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»v«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mn mathvariant=¨bold¨»4«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»v«/mi»«mn mathvariant=¨bold¨»4«/mn»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»4«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»(«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mn mathvariant=¨bold¨»25«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»20«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
نصف الحركة في الرسم البياني للتسارع كدالة زمنية ، وفقًا للتسارع الذي وجدناه ووفقًا للأزمنة التي يتحرك فيها الجسم في كل جزء من الحركة:
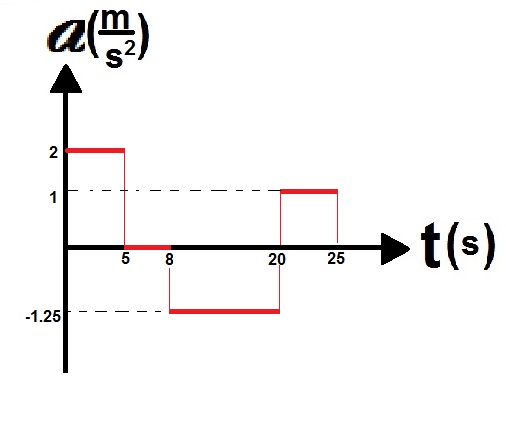
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
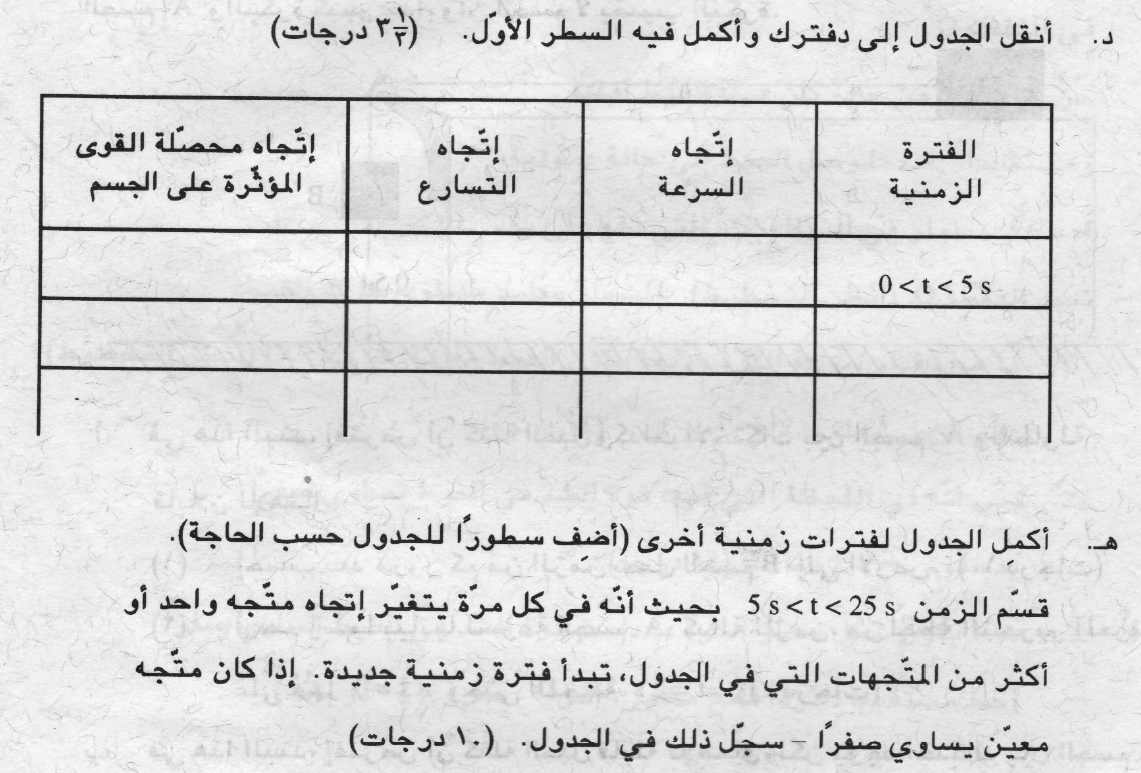
* يتناول القسمان د و هـ موضوع المتجهات والديناميكا ، ولا يمكن الإجابة على هذه الأقسام باستخدام مبادئ الكينماتيكا وحدها.
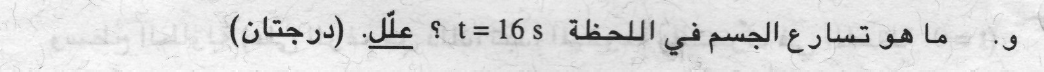
______________________________________________________________________________________
نجد التسارع بواسطة حساب ميل الرسم البياني بين الزمن t = 8s و t = 20s.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»v«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
إذن ، فإن تسارع الجسم في اللحظة t = 16s تساوي 1.25 مترًا لكل ثانية تربيع.
في اللحظة t=16s ، تكون سرعة الجسم تساوي صفرًا ولكن يوجد تسارع للجسم.
______________________________________________________________________________________
19. 1995.1- جدول ورسم بياني للموقع كدالة للزمن

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
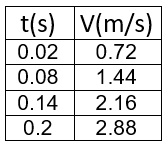
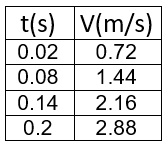
______________________________________________________________________________________

______________________________________________________________________________________
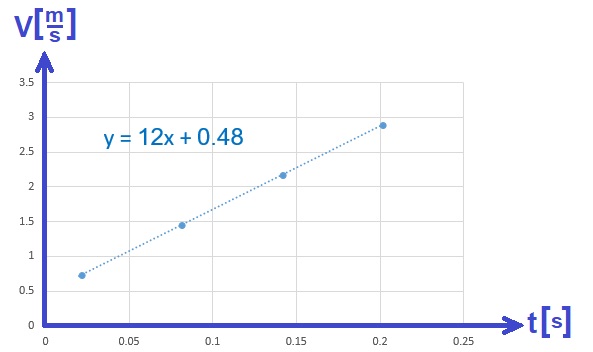

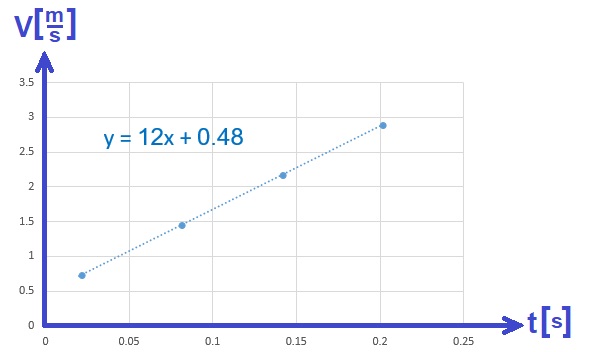
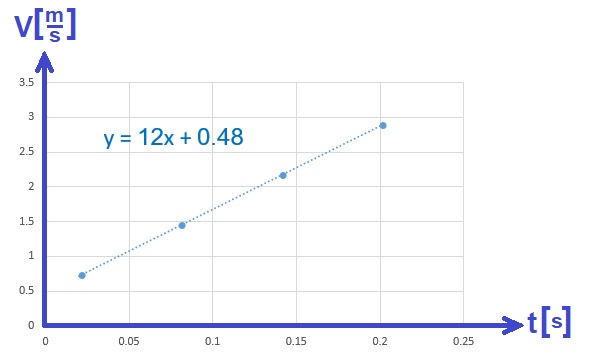
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
20. 1994,1- حركة البالستية - المنطاد

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
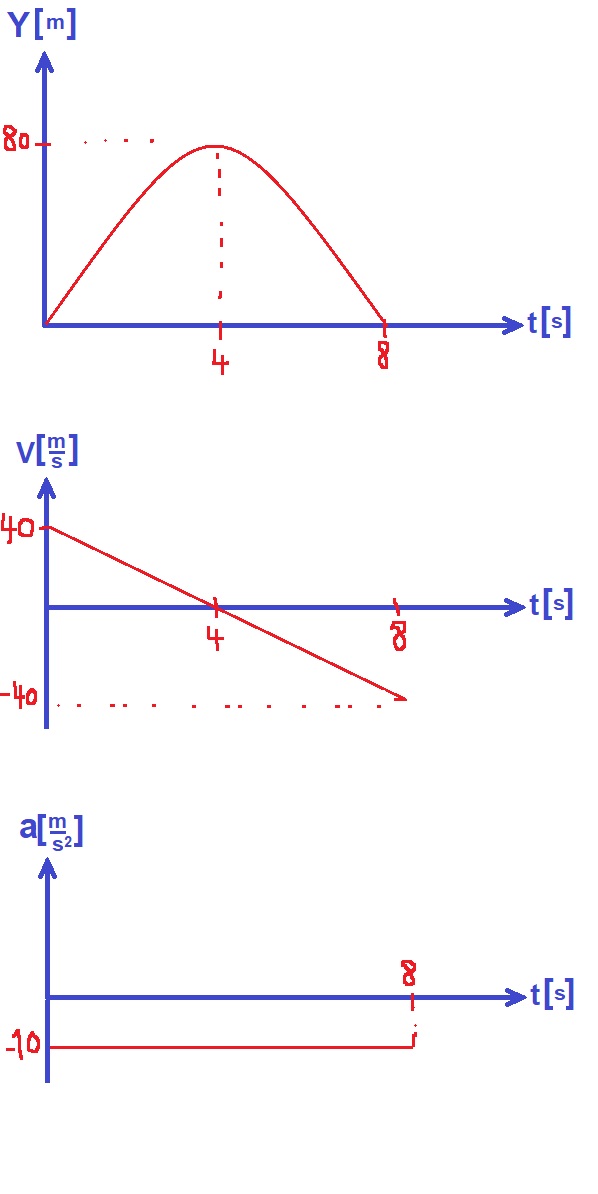

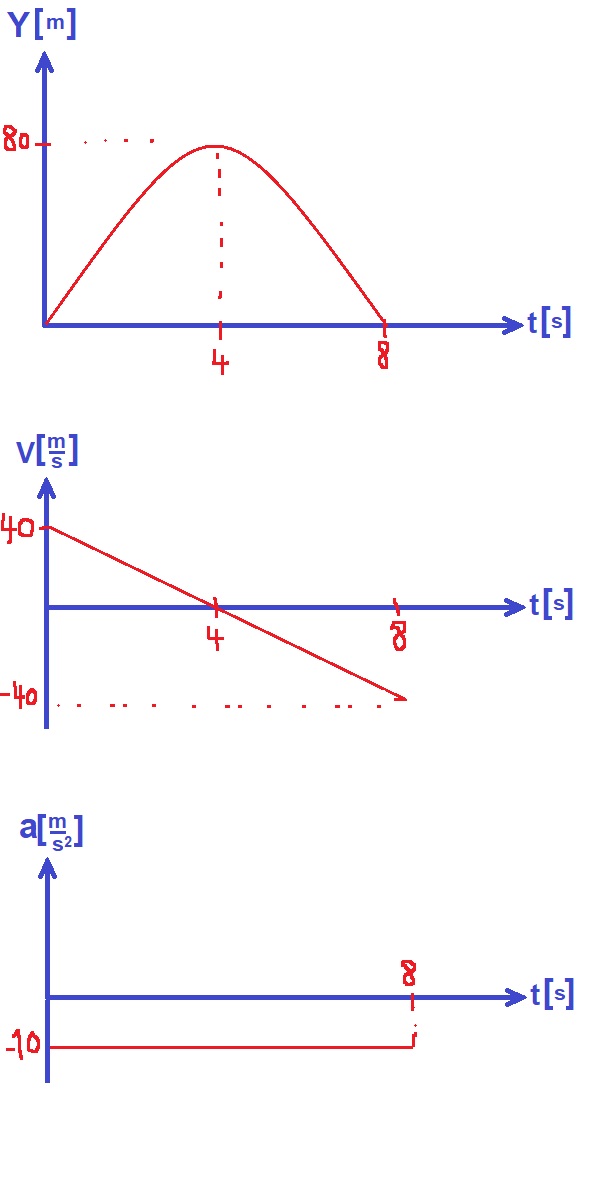
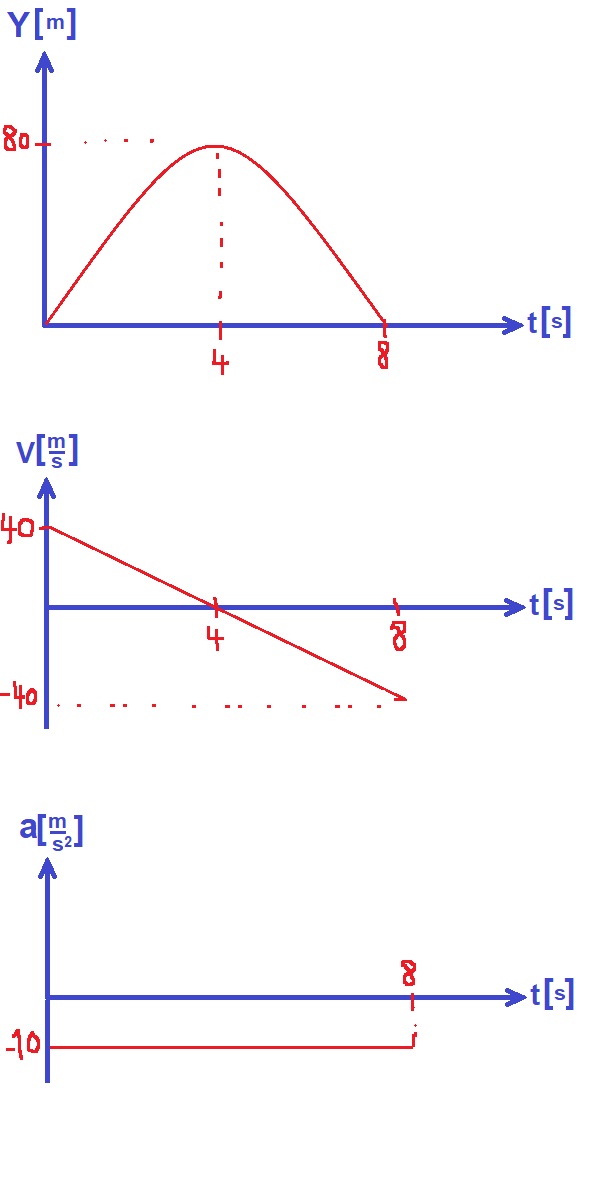
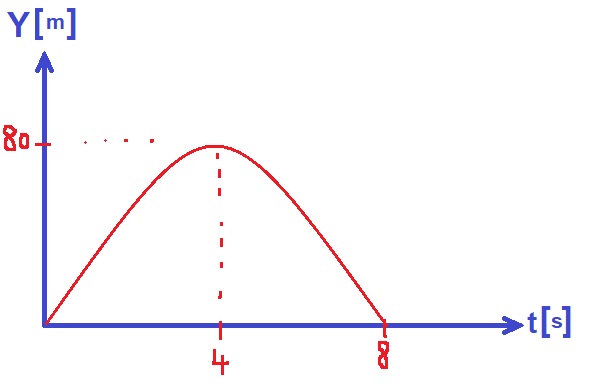
في هذا الرسم البياني، الميل يساوي التسارع، وبما أن التسارع ثابت، فإن الميل ثابت.
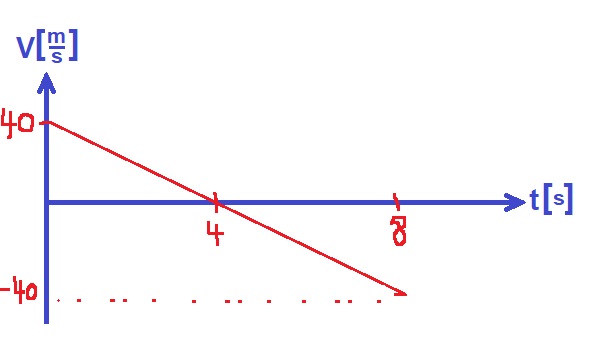
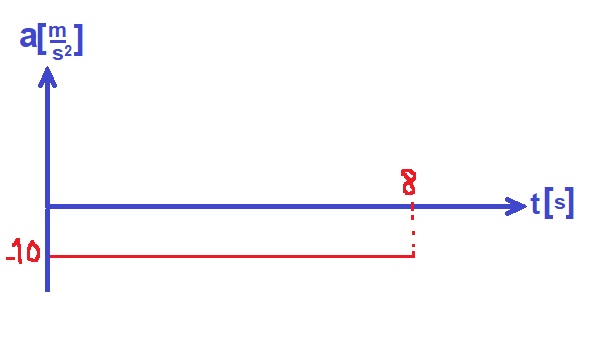



______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
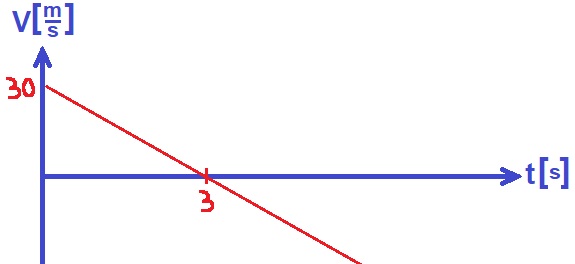
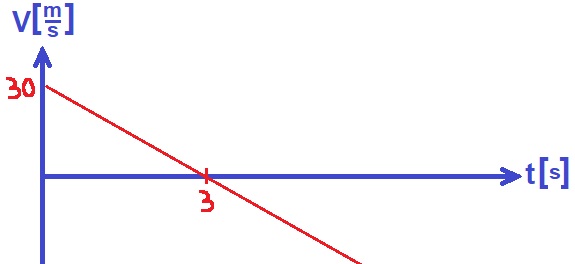

______________________________________________________________________________________
21. 1992,1- رسم بياني للسرعة كدالة للزمن لحركة مصعد
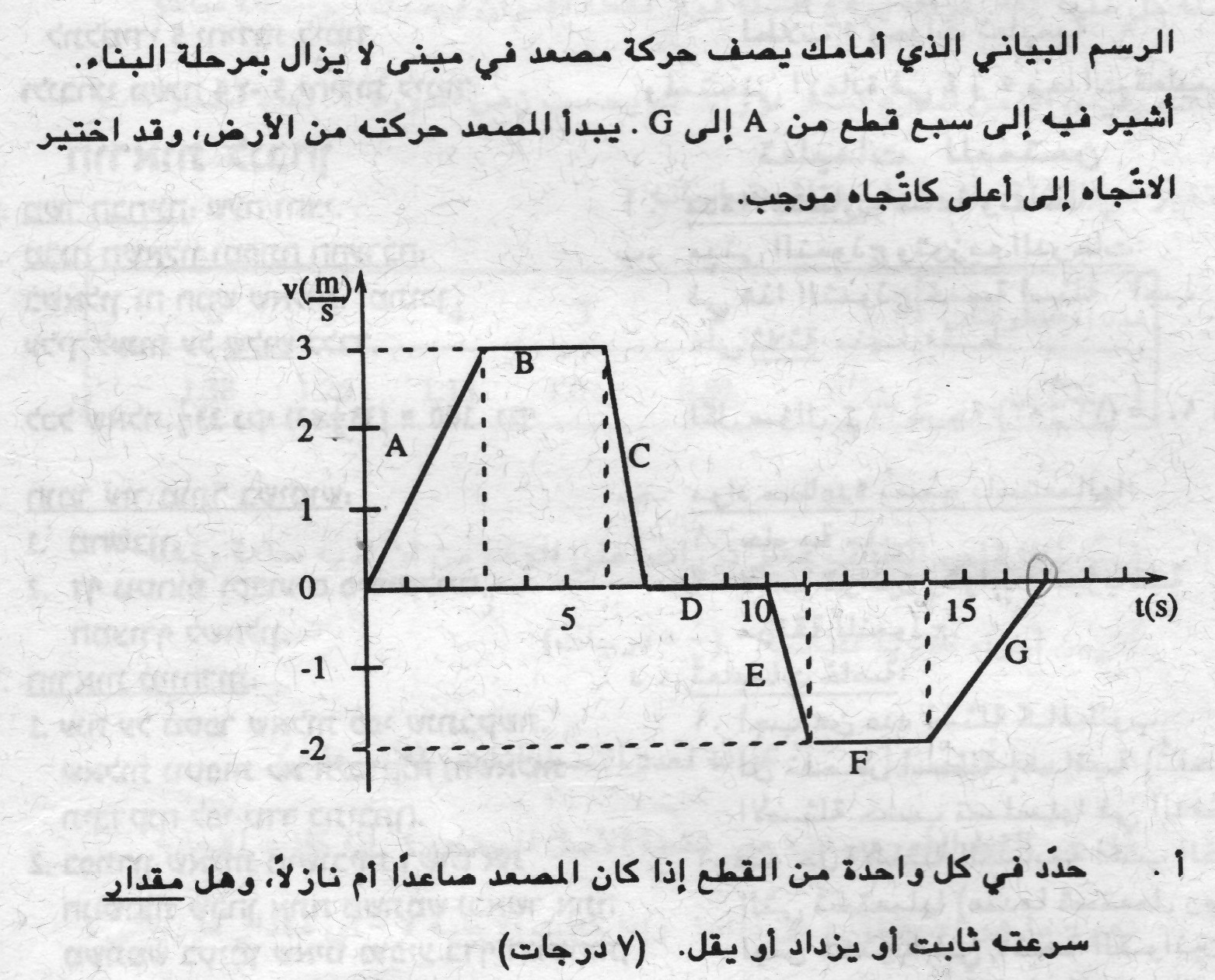
______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

* يتناول هذا السؤال موضوع الوزن الوهمي المتضمن في فصل الديناميكا. لا يمكن الإجابة على هذا السؤال باستخدام مبادئ الكينماتيكا وحدها!
22. 1988,1-الرسم البياني للسرعة كدالة للزمن ، خط المستقيم
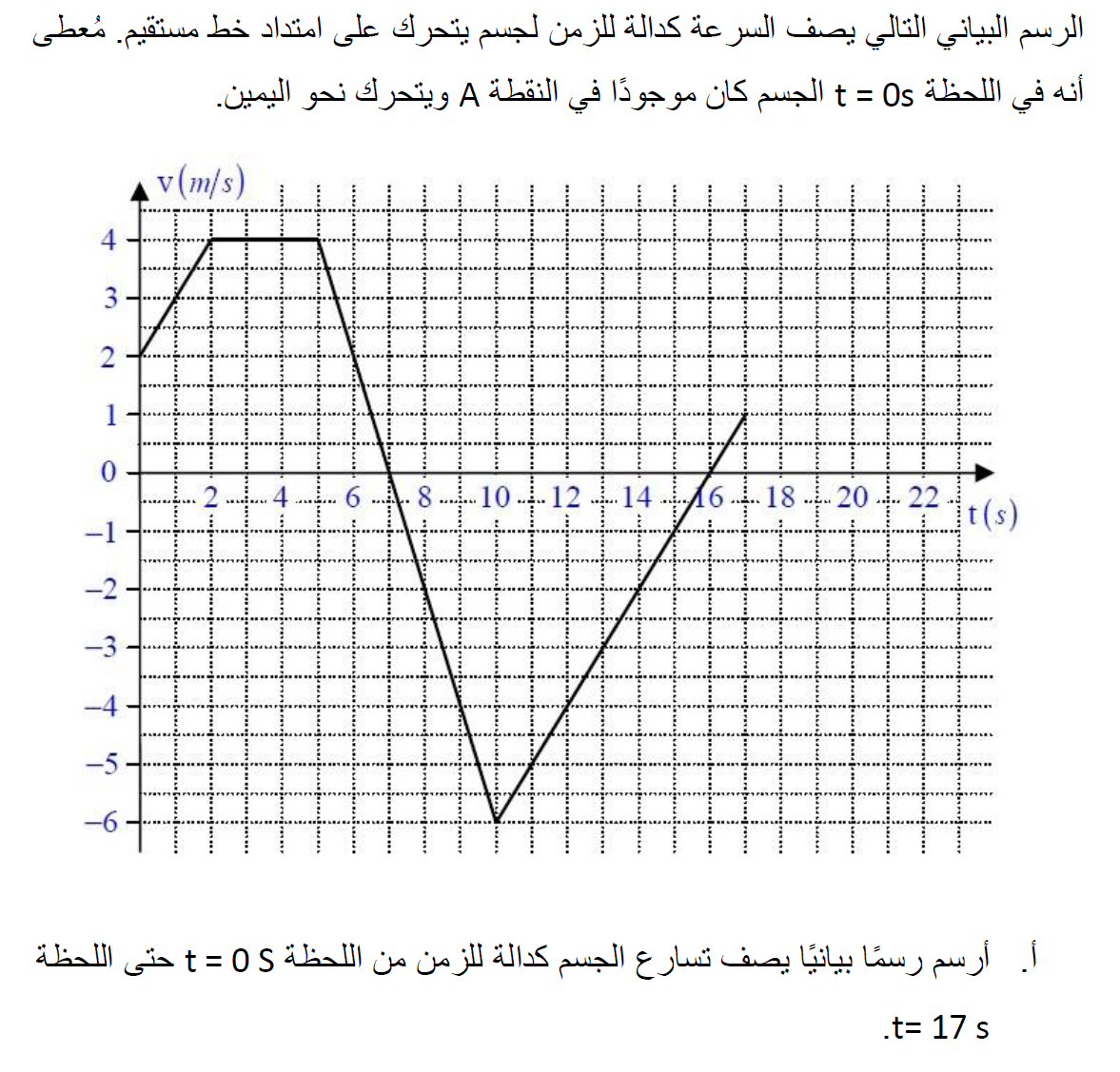
______________________________________________________________________________________
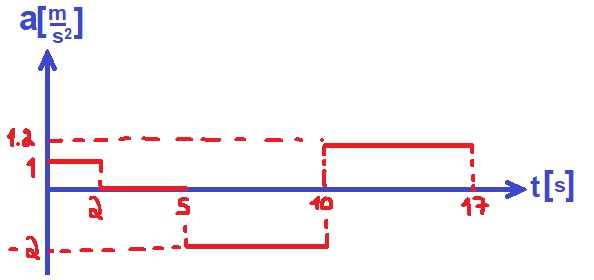
نجد التسارع بالفترة الزمنية
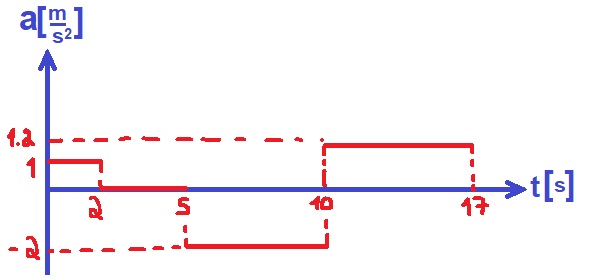
נמצא את התאוצה בזמנים undefined :

______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
23. 1984,17- الرسم البياني للسرعة كدالة للزمن، الخط المستقيم

______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
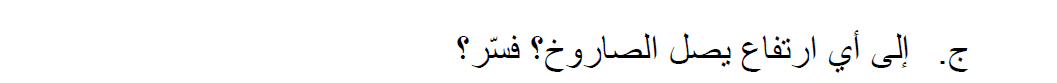
______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

*يتناول هذا القسم موضوع الديناميكا ، بمساعدة الكينماتيكا وحدها لا يمكن الإجابة على هذا السؤال.
[[forum(2972,0,0,1)]]