حلول التدريبات العملية كينماتيكا - رسوم بيانية نوعية

الرسم البياني المعطى هو رسم بياني للسرعة كدالة للزمن.

في الرسم البياني للسرعة كدالة للزمن، يكون ميل الدالة الموصوفة في الرسم البياني مساويًا لتسارع الجسم ، والمساحة المحصورة بين الدالة ومحور الزمن تساوي ازاحة الحركة.

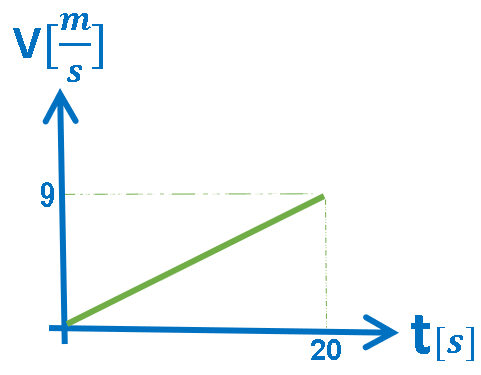
رياضياً: الرسم البياني يصف دالة خطية ذات ميل ثابت.

نحسب تسارع الجسم بواسطة حساب ميل الدالة في الرسم البياني:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»v«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»45«/mn»«mstyle displaystyle=¨false¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/menclose»«/mstyle»«/math»

نحسب ازاحة الجسم من المساحة المحصورة بين الدالة والمحور الزمني:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»90«/mn»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mstyle»«/math»

باختصار: يبدأ الجسم في التحرك من حالة السكون: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»0«/mn»«mfrac mathcolor=¨#FF6600¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math», بتسارع ثابت وموجب:  «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»45«/mn»«mfrac mathcolor=¨#FF6600¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math» , لمدة 20 ثانية.

يتحرك الجسم في اتجاه محور الحركة ويقطع ازاحة مقدارها 90 مترًا.