حلول التدريبات العملية كينماتيكا - رسوم بيانية نوعية
| الموقع: | YouCube |
| المقرر: | קינמטיקה בקו ישר - ערבית |
| كتاب: | حلول التدريبات العملية كينماتيكا - رسوم بيانية نوعية |
| طبع بواسطة: | משתמש אורח |
| التاريخ: | الأربعاء، 4 فبراير 2026، 4:20 AM |
جدول المحتويات
- 1.أ- الرسم البياني لـ X(t), لجسم ساكن.
- 1.ب- الرسم البياني V(t), في حركة منتظمة السرعة
- 2.أ- رسم بياني V(t), حركة بتسارع ثابت.
- 2.ب- الرسم البياني X(t), لحركة بسرعة ثابتة
- 3.أ- رسم بياني V(t), حركة بتسارع ثابت.
- 3.ب- الرسم البياني X(t), لحركة بسرعة ثابتة
- 4.أ- الرسم البياني V(t), حركة بتسارع ثابت.
- 4.ب-الرسم البياني X(t), لحركة بسرعة ثابتة
- 5.أ- الرسم البياني V(t), حركة بتسارع متغير.
- 5.ب- الرسم البياني X(t), حركة بتسارع سالب.
- 6.أ- الرسم البياني X(t), ثلاث مراحل حركية.
- 6.ب- الرسم البياني V(t), ثلاث حركات مختلفة.
- 7.أ- الرسم البياني V(t), حركة منتظمة على مراحل.
- 7.ب- الرسم البياني X(t), يستقر الجسم في مكانين مختلفين.
- 8.أ- الرسم البياني V(t), حركة منتظمة على مراحل.
- 8 ب- الرسم البياني X(t), يستقر الجسم في مكانين مختلفين.
- 9.أ- الرسم البياني V(t),خمس حركات مختلفة.
- 9.ب- الرسم البياني X(t),خمس حركات مختلفة.
- 10.أ- الرسم البياني V(t), حركة بتسارع متغير.
- 10.ب- الرسم البياني X(t),حركة بسرعة متغيرة.
- 11.أ- الرسم البياني X(t),حركة بسرعة متغيرة.
- 11.ب- الرسم البياني V(t), حركة بتسارع متغير.
1.أ- الرسم البياني لـ X(t), لجسم ساكن.
الرسم البياني المعطى هو رسم بياني للموقع كدالة للزمن.
في الرسم البياني للمكان كدالة للزمن، يكون ميل الدالة في الرسم البياني مساويًا لسرعة الجسم.
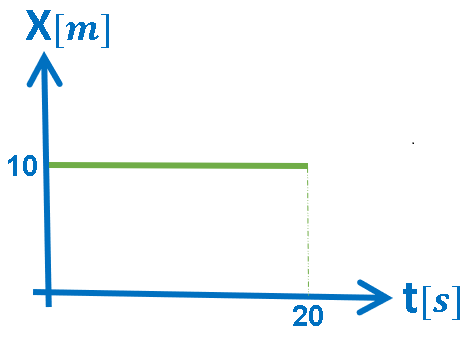
رياضياً: يصف الرسم البياني دالة ذات قيمة ثابتة.
الخلاصة: يستقر الجسم في الموقع X = 10 م لمدة 20 ثانية.
1.ب- الرسم البياني V(t), في حركة منتظمة السرعة
الرسم البياني المعطى هو رسم بياني للسرعة كدالة للزمن.
في الرسم البياني للسرعة كدالة زمنية، يكون ميل الدالة الموصوفة في الرسم البياني مساويًا لتسارع الجسم ، والمساحة المحصورة تساوي الازاحة.
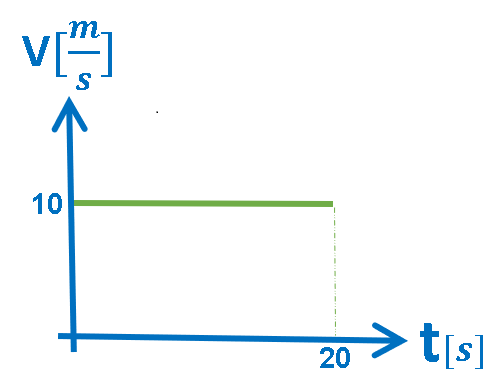
رياضياً: يصف الرسم البياني دالة ذات قيمة ثابتة.
للتلخيص: سرعة الجسم 10 أمتار في الثانية ، يتحرك الجسم بسرعة ثابتة لمدة 20 ثانية.
2.أ- رسم بياني V(t), حركة بتسارع ثابت.
الرسم البياني التالي يصف السرعة كدالة للزمن.
في الرسم البياني للسرعة كدالة للزمن، ميل الدالة الموصوفة في الرسم البياني مساويًا لتسارع الجسم والمساحة المحصورة تساوي الازاحة.
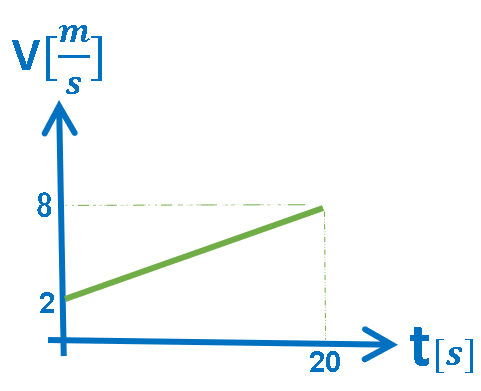
رياضياً: هذا الرسم البياني يصف دالة خطية ذات ميل ثابت.
نحسب تسارع الجسم بواسطة حساب ميل الرسم البياني:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#916;v«/mi»«mi mathvariant=¨bold¨»§#916;t«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«mstyle mathvariant=¨bold¨ displaystyle=¨false¨»«mfrac»«mi»m«/mi»«msup»«mi»s«/mi»«mn»2«/mn»«/msup»«/mfrac»«/mstyle»«/menclose»«/mstyle»«/math»
نحسب ازاحة الجسم حسب المساحة المحصورة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1606;§#1581;§#1585;§#1601;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1588;§#1576;§#1607;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1605;§#1587;§#1575;§#1581;§#1577;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#215;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»100«/mn»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mstyle»«/math»
للتلخيص: بدأ الجسم يتحرك من سرعة ابتدائية 2 متر في الثانية، بتسارع ثابت قدره «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»3«/mn»«mfrac mathcolor=¨#FF6600¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/math» لمدة 20 ثانية.
ازاحة الجسم مساوية 100 متر.
2.ب- الرسم البياني X(t), لحركة بسرعة ثابتة
الرسم البياني المعطى هو رسم بياني للموقع كدالة للزمن.
في التمثيل البياني للموقع كدالة للزمن، يكون ميل الدالة في الرسم البياني مساويًا لسرعة الجسم.
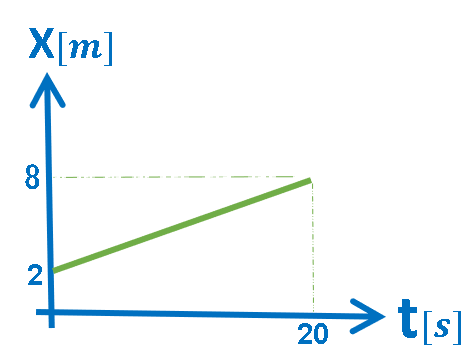
رياضياً: هذا الرسم البياني يصف دالة خطية ميلها ثابت.
نحسب سرعة الجسم بواسطة حساب ميل الدالة الموصوفة في الرسم البياني
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#916;x«/mi»«mi mathvariant=¨bold¨»§#916;t«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«mstyle mathvariant=¨bold¨ displaystyle=¨false¨»«mfrac»«mi»m«/mi»«mi»s«/mi»«/mfrac»«/mstyle»«/menclose»«/math»
للتلخيص: يبدأ الجسم في التحرك من نقطة البداية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»X«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»m«/mi»«/mstyle»«/math», وهو يتحرك بسرعة ثابتة مقدارها «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»3«/mn»«mfrac mathcolor=¨#FF6600¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mstyle»«/math» لمدة 20 ثانية.
ازاحة الجسم مساوية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»m«/mi»«/mstyle»«/math».
3.أ- رسم بياني V(t), حركة بتسارع ثابت.
الرسم البياني المعطى هو رسم بياني للسرعة كدالة للزمن.
في الرسم البياني للسرعة كدالة للزمن، يكون ميل الدالة الموصوفة في الرسم البياني مساويًا لتسارع الجسم ، والمساحة المحصورة بين الدالة ومحور الزمن تساوي ازاحة الحركة.
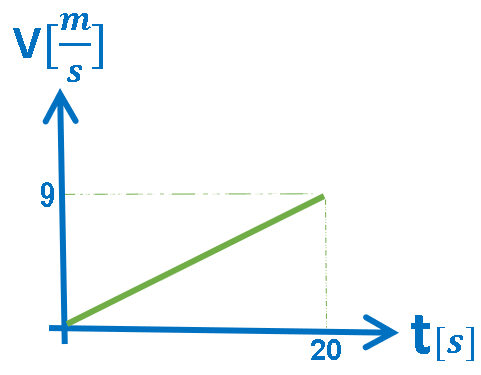
رياضياً: الرسم البياني يصف دالة خطية ذات ميل ثابت.
نحسب تسارع الجسم بواسطة حساب ميل الدالة في الرسم البياني:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»v«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»45«/mn»«mstyle displaystyle=¨false¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/menclose»«/mstyle»«/math»
نحسب ازاحة الجسم من المساحة المحصورة بين الدالة والمحور الزمني:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»90«/mn»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mstyle»«/math»
باختصار: يبدأ الجسم في التحرك من حالة السكون: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»0«/mn»«mfrac mathcolor=¨#FF6600¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math», بتسارع ثابت وموجب: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»45«/mn»«mfrac mathcolor=¨#FF6600¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math» , لمدة 20 ثانية.
يتحرك الجسم في اتجاه محور الحركة ويقطع ازاحة مقدارها 90 مترًا.
3.ب- الرسم البياني X(t), لحركة بسرعة ثابتة
الرسم البياني المعطى هو رسم بياني للموقع كدالة للزمن.
في الرسم البياني للموقع كدالة للزمن، يكون ميل الدالة الموصوفة مساويًا لسرعة الجسم.
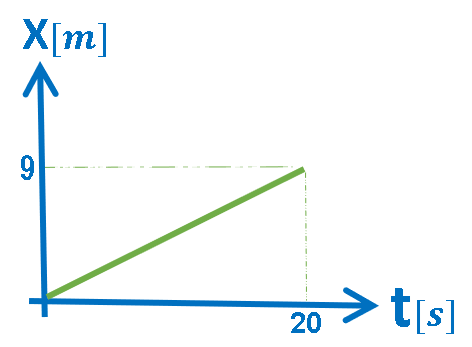
رياضياً: الرسم البياني يصف دالة ذات ميل ثابت.
يُمثّل ميل الرسم البياني للموقع كدالة للزمن وتيرة تغيّر الموقع ويساوي سرعة الجسم.
ميل الرسم البياني ثابت، لذا يتحرك الجسم بسرعة ثابتة.
نحسب سرعة الجسم بواسطة حساب ميل الرسم البياني:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»45«/mn»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨ displaystyle=¨false¨»«mfrac»«mi»m«/mi»«mi»s«/mi»«/mfrac»«/mstyle»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»45«/mn»«mstyle mathvariant=¨bold¨ displaystyle=¨false¨»«mfrac»«mi»m«/mi»«mi»s«/mi»«/mfrac»«/mstyle»«/menclose»«/mstyle»«/math»
الخلاصة: يبدأ الجسم في التحرك من نقطة الأصل لمحور الحركة، بسرعة ثابتة مقدارها«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»45«/mn»«mstyle mathvariant=¨bold¨ mathcolor=¨#FF6600¨ displaystyle=¨false¨»«mfrac»«mi»m«/mi»«mi»s«/mi»«/mfrac»«/mstyle»«/mstyle»«/math» لمدة 20 ثانية.
ازاحة الجسم «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»9«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»m«/mi»«/mstyle»«/math».
4.أ- الرسم البياني V(t), حركة بتسارع ثابت.
الرسم البياني المعطى هو رسم بياني للسرعة
كدالة للزمن.
في الرسم البياني للسرعة كدالة للزمن، يكون ميل الدالة الموصوفة في الرسم البياني مساويًا لتسارع الجسم، والمساحة المحصورة بين الدالة ومحور الزمن تساوي ازاحة الحركة.
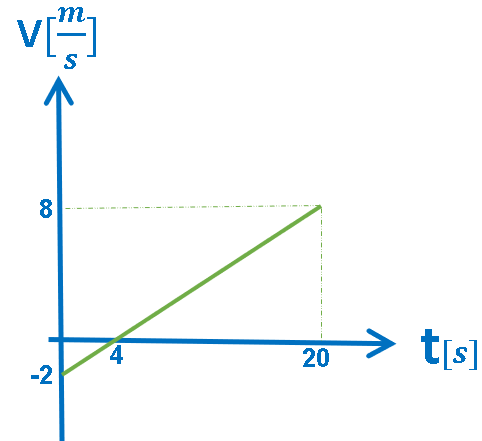
رياضياً: الرسم البياني يصف دالة خطية ذات ميل ثابت وموجب.
نحسب
تسارع الجسم بواسطة حساب ميل الدالة الموصوفة في الرسم البياني:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»v«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»(«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»20«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨ displaystyle=¨false¨»«mfrac»«mi»m«/mi»«msup»«mi»s«/mi»«mn»2«/mn»«/msup»«/mfrac»«/mstyle»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mstyle displaystyle=¨false¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/menclose»«/mstyle»«/math»
نحسب ازاحة الجسم من المساحة المحصورة بين الدالة والمحور الزمني:
תחילה הגוף נע במהירות שלילית ולאחר מכן הוא משנה את כיוון תנועתו ונע במהירות חיובית.
في البداية، يتحرك الجسم بسرعة سالبة ثم يغير اتجاه حركته ويتحرك بسرعة موجبة.
نحسب ازاحة حركة الجسم خلال الثواني الأربع الأولى، في حركته عكس اتجاه المحور «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«/mstyle»«/math»:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#215;«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/mstyle»«/math»
نحسب ازاحة حركة الجسم في حركته باتجاه المحور «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«/mstyle»«/math»:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»16«/mn»«mo mathvariant=¨bold¨»§#215;«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»64«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/mstyle»«/math»
نحسب الإزاحة الكلية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«/mstyle»«/math»:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»64«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»60«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»X«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»60«/mn»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mstyle»«/math»
الخلاصة: بدأ الجسم يتحرك من سرعة ابتدائية مقدارها «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»2«/mn»«mfrac mathcolor=¨#FF6600¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math» , وهو يتحرك بتسارع ثابت مقداره «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»45«/mn»«mfrac mathcolor=¨#FF6600¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math», لمدة 20 ثانية.
يتحرك الجسم في الثواني الأربع الأولى بسرعة سالبة ، ويتحرك عكس اتجاه المحور.
في اللحظة t = 4s ، يتوقف الجسم توقفًا لحظيًا ثم يغير اتجاه حركته ويتحرك في اتجاه المحور (بنفس التسارع) لمدة 16 ثانية أخرى.
ازاحة الجسم الكلية 60 مترا.
4.ب-الرسم البياني X(t), لحركة بسرعة ثابتة
الرسم البياني المعطى يمثل الموقع كدالة للزمن.
ميل الرسم البياني للموقع كدالة للزمن، يكون مساويًا لسرعة الجسم.
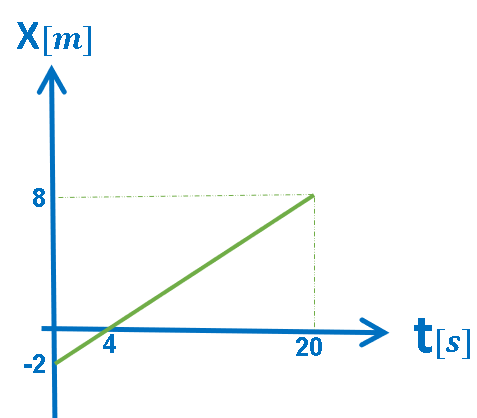
رياضياً: الرسم البياني يصف دالة ذات ميل ثابت وموجب.
نحسب سرعة الجسم بواسطة حساب ميل الرسم البياني:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1513;§#1497;§#1508;§#1493;§#1506;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»(«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨ displaystyle=¨false¨»«mfrac»«mi»m«/mi»«mi»s«/mi»«/mfrac»«/mstyle»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mstyle displaystyle=¨false¨ mathvariant=¨bold¨»«mfrac»«mi»m«/mi»«mi»s«/mi»«/mfrac»«/mstyle»«/menclose»«/mstyle»«/math»
خلاصة: الجسم يتحرك من الموقع «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»X«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»m«/mi»«/mstyle»«/math» بسرعو ثابتة مقدارها«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»5«/mn»«mfrac mathcolor=¨#FF6600¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mstyle»«/math» .
يتحرك الجسم في الاتجاه الموجب للمحور طوال مدة الحركة، وتكون ازاحة الجسم 10 أمتار.
5.أ- الرسم البياني V(t), حركة بتسارع متغير.
الرسم البياني المعطى هو رسم بياني للسرعة
كدالة للزمن.
في الرسم البياني للسرعة كدالة للزمن، يكون ميل الدالة الموصوفة في الرسم البياني مساويًا لتسارع الجسم، والمساحة المحصورة بين الدالة ومحور الزمن تساوي ازاحة الحركة.
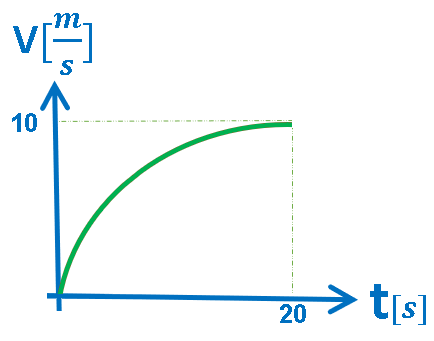
رياضياً: الرسم البياني يصف دالة غير خطية ميلها آخذ بالنقصان.
خلاصة: يتحرك الجسم من حالة السكون لمدة 20 ثانية بسرعة متزايدة وبتسارع موجب آخذ بالنقصان.
في نهاية الحركة تكون سرعة الجسم «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»10«/mn»«mfrac mathcolor=¨#FF6600¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mstyle»«/math», يتضح من الرسم البياني أن تسارع الجسم في هذه اللحظة يساوي صفرًا.
5.ب- الرسم البياني X(t), حركة بتسارع سالب.
الرسم البياني المعطى هو رسم بياني للموقع كدالة للزمن.
في الرسم البياني للموقع كدالة للزمن، يكون ميل الدالة مساويًا لسرعة الجسم.
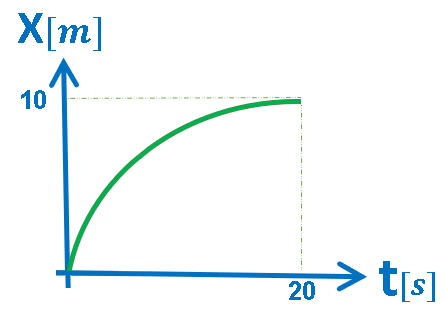
رياضياً: الرسم البياني يصف دالة غير خطية ميلها آخذ بالنقصان.
خلاصة: يتحرك الجسم من نقطة بداية المحور لمدة 20 ثانية بسرعة آخذة بالنقصان بتسارع سالب.
في نهاية الحركة، يصل الجسم إلى الموقع X = 10m من الرسم البياني، سرعة الجسم في هذه اللحظة تساوي صفرًا .
6.أ- الرسم البياني X(t), ثلاث مراحل حركية.
الرسم البياني المعطى هو رسم بياني للموقع كدالة للزمن.
في الرسم البياني للموقع كدالة للزمن، يكون ميل الدالة الموصوفة مساويًا لسرعة الجسم.
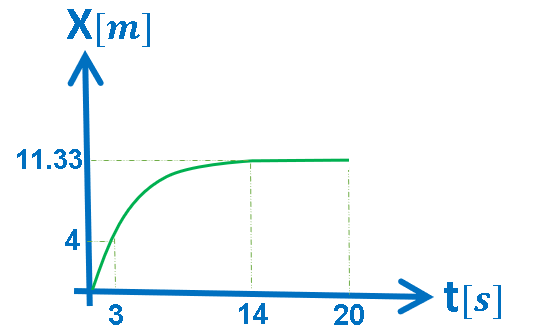
يمكن تقسيم الدالة الموصوفة في الرسم البياني إلى ثلاثة مراحل مختلفة:
في المرحلة الأولى: بالفترة الزمنية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mn mathvariant=¨bold¨»3«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»: ميل الدالة موجب وثابت.
في المرحلة الثانية: بالفترة الزمنية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»3«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#8804;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#8804;«/mo»«mn mathvariant=¨bold¨»14«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»: ميل الدالةآخذ بالنقصان حتى يصل إلى الصفر.
في المرحلة الثانية: بالفترة الزمنية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»14«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#8804;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#8804;«/mo»«mn mathvariant=¨bold¨»20«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»: مقدار الدالة ثابت.
نحسب سرعة الجسم في المرحلة الأولى من الحركة من ميل الرسم البياني:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»v«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨ displaystyle=¨false¨»«mfrac»«mi»m«/mi»«mi»s«/mi»«/mfrac»«/mstyle»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold-italic¨»V«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»33«/mn»«mstyle mathvariant=¨bold¨ displaystyle=¨false¨»«mfrac»«mi»m«/mi»«mi»s«/mi»«/mfrac»«/mstyle»«/menclose»«/mstyle»«/math»
خلاصة: خلال الثواني الثلاث الأولى، يتحرك الجسم من نقطة بداية المحور بسرعة ثابتة مقدارها «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»33«/mn»«mfrac mathcolor=¨#FF6600¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mstyle»«/math»على طول ازاحة مقدارها 4 أمتار.
في المرحلة الثانية، يتحرك الجسم بسرعة متناقصة من السرعة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»33«/mn»«mfrac mathcolor=¨#FF6600¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mstyle»«/math» وحتى توقفها.
في المرحلة الثالثة، يتوقف الجسم عن الحركة لمدة ست ثوانٍ في هذا الموقع X=11.33m .
6.ب- الرسم البياني V(t), ثلاث حركات مختلفة.
الرسم البياني المعطى هو رسم بياني للسرعة كدالة للزمن.
في الرسم البياني للسرعة كدالة للزمن، يكون ميل الدالة الموصوفة في الرسم البياني مساويًا لتسارع الجسم، والمساحة المحصورة بين الدالة ومحور الزمن تساوي ازاحة الحركة.
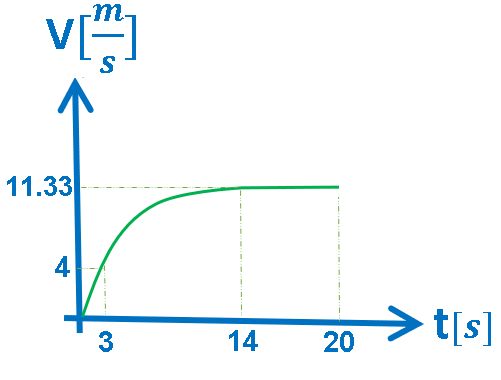
رياضياً: يمكن تقسيم الدوال الموصوفة في الرسم البياني إلى ثلاث دوال مختلفة:
الدالة الأولى: بالفترة الزمنية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mn mathvariant=¨bold¨»3«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»: ميل الدالة موجب وثابت.
الدالة الثانية: بالفترة الزمنية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»3«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#8804;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#8804;«/mo»«mn mathvariant=¨bold¨»14«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»: ميل الدالة آخذ بالنقصان حتى يصل إلى الصفر.
الدالة الثالثة: بالفترة الزمنية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»14«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#8804;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#8804;«/mo»«mn mathvariant=¨bold¨»20«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»: قيمة الدالة ثابتة.
نحسب تسارع الجسم في الجزء الأول من الحركة من ميل الدالة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»v«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨ displaystyle=¨false¨»«mfrac»«mi»m«/mi»«msup»«mi»s«/mi»«mn»2«/mn»«/msup»«/mfrac»«/mstyle»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»33«/mn»«mstyle mathvariant=¨bold¨ displaystyle=¨false¨»«mfrac»«mi»m«/mi»«msup»«mi»s«/mi»«mn»2«/mn»«/msup»«/mfrac»«/mstyle»«/menclose»«/mstyle»«/math»
نحسب ازاحة الحركة في مقطع الحركة الأول من المساحة المحصورة في الثواني الثلاث الأولى:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1587;§#1575;§#1581;§#1577;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»6«/mn»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mstyle»«/math»
نحسب ازاحة الحركة في مقطع الحركة الثالث من المساحة المحصورة في الثواني الست ثواني الأولى:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1587;§#1575;§#1581;§#1577;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»11«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»67«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»98«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»98«/mn»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mstyle»«/math»
خلاصة: خلال ألـ 20 ثانية ، يتحرك الجسم في ثلاث حركات مختلفة.
في المرحلة الأولى ، يتحرك الجسم من حالة السكون بتسارع ثابت مقداره «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»33«/mn»«mfrac mathcolor=¨#FF6600¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/math» على طول ازاحة مقدارها 6 أمتار.
في المرحلة الثانية ، يتحرك الجسم بسرعة آخذة بالازدياد (مع تسارع آخذ بالنقصان) من سرعة 4 أمتار في الثانية إلى 11.33 مترًا في الثانية.
في المرحلة الثالثة ، يتحرك الجسم بسرعة ثابتة مقدارها 11.33 مترًا في الثانية لمدة 6 ثوانٍ على طول ازاحة مقدارها 67.98 مترًا.
7.أ- الرسم البياني V(t), حركة منتظمة على مراحل.
الرسم البياني المعطى هو رسم بياني للسرعة
كدالة للزمن.
في الرسم البياني للسرعة كدالة للزمن، يكون ميل الدالة الموصوفة في الرسم البياني مساويًا لتسارع الجسم، والمساحة المحصورة بين الدالة ومحور الزمن تساوي ازاحة الحركة.
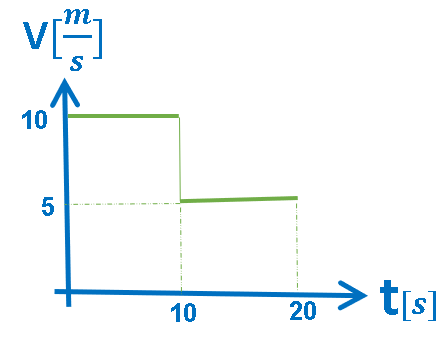
رياضيا: تم وصف دالتين ثابتتين في الرسم البياني.
الدالة الأولى, بالفترة الزمنية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mn mathvariant=¨bold¨»10«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»: دالة ثابتة مقدارها 10 متر.
الدالة الثانية, بالفترة الزمنية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»10«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mn mathvariant=¨bold¨»20«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»: دالة ثابتة مقدارها 5 متر.
نحسب ازاحة الحركة في مقطع الحركة الأول «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math», من المساحة المحصورة في الثواني العشر الأولى:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1605;§#1587;§#1575;§#1581;§#1577;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»100«/mn»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mstyle»«/math»
نحسب ازاحة الحركة في مقطع الحركة الثاني «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math», من المساحة المحصورة في الثواني العشر الثانية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1513;§#1496;§#1495;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»50«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»50«/mn»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mstyle»«/math»
بعد ذلك، يتحرك الجسم بسرعة ثابتة مقدارها 5 أمتار في الثانية، لمدة 10 ثوانٍ، على طول ازاحة 50 مترًا.
7.ب- الرسم البياني X(t), يستقر الجسم في مكانين مختلفين.
الرسم البياني المعطى هو رسم بياني للموقع كدالة للزمن.
في الرسم البياني للموقع كدالة للزمن، يكون ميل الدالة الموصوفة مساويًا لسرعة الجسم.
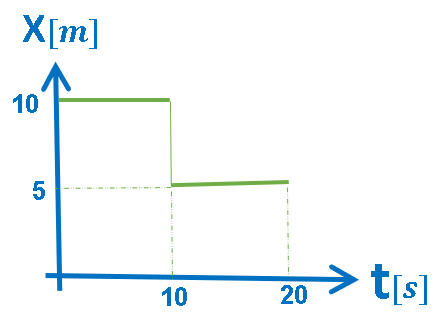
رياضيا: الرسم البياني يصف دالتين ثابتتين مع الزمن.
الدالة الأولى: خلال الفترة الزمنية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mn mathvariant=¨bold¨»10«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»: الدالة ثابتة ومقدارها 10 متر.
الدالة الثانية: خلال الفترة الزمنية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»10«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mn mathvariant=¨bold¨»20«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»: الدالة ثابتة ومقدارها 5 متر.
ميل كلتا الدالتين هو صفر. سرعة الجسم في مقطع الحركة الأول وأيضًا في المقطع الثاني للحركة يساوي صفرًا.
ملخص الحركة: لا يتحرك الجسم، يكون في حالة سكون في مكانين مختلفين.
أولاً، يكون الجسم ساكنًا لمدة 10 ثوانٍ في الموقع X=10m، ثم يستقر الجسم لمدة 10 ثوانٍ في الموقع X = 5m.
8.أ- الرسم البياني V(t), حركة منتظمة على مراحل.
الرسم البياني المعطى هو رسم بياني للسرعة كدالة للزمن.
في الرسم البياني للسرعة كدالة للزمن، يكون ميل الدالة الموصوفة في الرسم البياني مساويًا لتسارع الجسم، والمساحة المحصورة بين الدالة ومحور الزمن تساوي ازاحة الحركة.
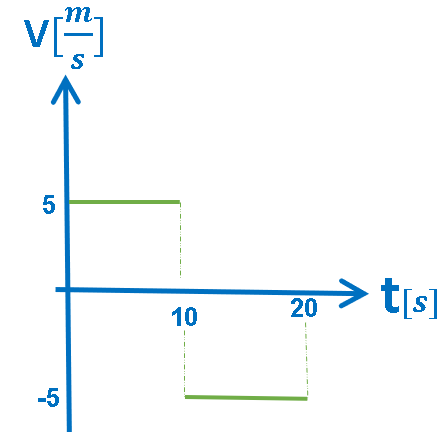
رياضيًا: يصف الرسم البياني دالتين ثابتتين.
الدالة الأولى, بالفترة الزمنية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mn mathvariant=¨bold¨»10«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»: دالة ثابتة مقدارها 5 متر.
الدالة الثانية, بالفترة الزمنية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»10«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mn mathvariant=¨bold¨»20«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»: دالة ثابتة مقدارها 5- متر.
نحسب ازاحة الحركة في مقطع الحركة الأول «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math», من المساحة المحصورة في الثواني العشر الأولى:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1587;§#1575;§#1581;§#1577;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»50«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»50«/mn»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mstyle»«/math»
نحسب ازاحة الحركة في مقطع الحركة الثاني «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math», من المساحة المحصورة في الثواني العشر الثانية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1587;§#1575;§#1581;§#1577;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»50«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»50«/mn»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mstyle»«/math»
بعد ذلك، يتحرك الجسم بسرعة ثابتة مقدارها 5 أمتار في الثانية، لمدة 10 ثوانٍ، على طول ازاحة متماثلة مقدارها 50 مترًا.
8 ب- الرسم البياني X(t), يستقر الجسم في مكانين مختلفين.
الرسم البياني المعطى هو رسم بياني للموقع كدالة للزمن.
في الرسم البياني للموقع كدالة للزمن، يكون ميل الدالة الموصوفة مساويًا لسرعة الجسم.
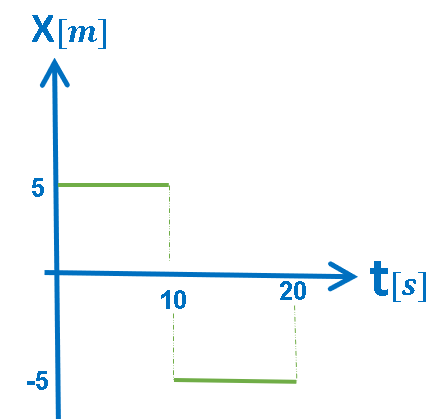
رياضيا: الرسم البياني يصف دالتين مختلفتين.
الدالة الأولى، خلال الفترة الزمنية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mn mathvariant=¨bold¨»10«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»: دالة ثابتة مقدارها 5 أمتار.
الدالة الثانية، خلال الفترة الزمنية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»10«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mn mathvariant=¨bold¨»20«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»: دالة ثابتة مقدارها 5 أمتار.
ملخص الحركة: لا يتحرك الجسم، بل يستقر في مكانين مختلفين.
أولاً ، يستقر الجسم لمدة 10 ثوانٍ في الموقع X=5m . ثم يستقر الجسم لمدة 10 ثوانٍ في الموقع X = -5m.
9.أ- الرسم البياني V(t),خمس حركات مختلفة.
الرسم البياني المعطى هو رسم بياني للسرعة كدالة للزمن.
في الرسم البياني للسرعة كدالة للزمن، يكون ميل الدالة الموصوفة في الرسم البياني مساويًا لتسارع الجسم، والمساحة المحصورة بين الدالة ومحور الزمن تساوي ازاحة الحركة.
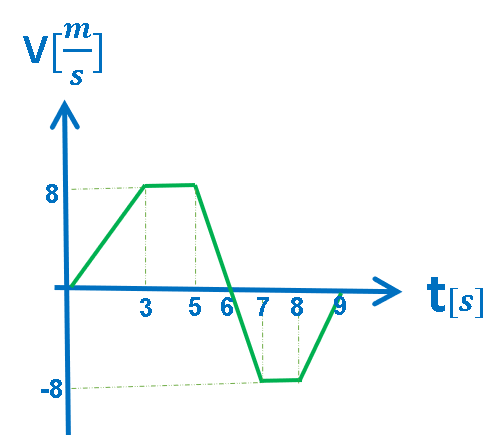
رياضيًا ، يصف الرسم البياني خمس دوال مختلفة:
الدالة الأولى, بالفترة الزمنية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mn mathvariant=¨bold¨»3«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»: دالة خطية تصاعدية.
الدالة الثانية, بالفترة الزمنية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»3«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»: دالة ثابتة مقدارها 8 أمتار في الثانية.
الدالة الثالثة, بالفترة الزمنية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»5«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mn mathvariant=¨bold¨»7«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»: دالة خطية تنازلية.
الدالة الرابعة, بالفترة الزمنية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»7«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mn mathvariant=¨bold¨»8«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»: دالة ثابتة مقدارها 8- أمتار في الثانية.
الدالة الخامسة, بالفترة الزمنية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»8«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mn mathvariant=¨bold¨»9«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»: دالة خطية تصاعدية.
الرسم البياني يصف خمس مراحل للحركة، نحسب التسارع والازاحة في كل مرحلة من المراحل الخمس للحركة.
- في المرحلة الأولى من الحركة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math» يتحرك الجسم بتسارع موجب وثابت.
نحسب تسارع الجسم في مرحلة الحركة الأولى، من ميل الدالة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»v«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»66«/mn»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨ displaystyle=¨false¨»«mfrac»«mi»m«/mi»«msup»«mi»s«/mi»«mn»2«/mn»«/msup»«/mfrac»«/mstyle»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»a«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»66«/mn»«mstyle mathvariant=¨bold¨ displaystyle=¨false¨»«mfrac»«mi»m«/mi»«msup»«mi»s«/mi»«mn»2«/mn»«/msup»«/mfrac»«/mstyle»«/menclose»«/mstyle»«/math»
نحسب ازاحة الحركة في المرحلة الأولى، من المساحة المحصورة في الثواني الثلاث الأولى:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1587;§#1575;§#1581;§#1577;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»x«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»12«/mn»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mstyle»«/math»
- في المرحلة الثانية من الحركة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math» الجسم يتحرك بسرعة ثابتة مقدارها 8 متر للثانية.
نحسب ازاحة الحركة في المرحلة الثانية، من المساحة المحصورة :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1587;§#1575;§#1581;§#1577;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»16«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»x«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»16«/mn»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mstyle»«/math»
- في المرحلة الثالثة من الحركة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math» الجسم يتحرك بتسارع ثابت وسالب.
نحسب تسارع الجسم في مرحلة الحركة الثالثة، من ميل الدالة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»v«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»7«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»16«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨ displaystyle=¨false¨»«mfrac»«mi»m«/mi»«msup»«mi»s«/mi»«mn»2«/mn»«/msup»«/mfrac»«/mstyle»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»a«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«mstyle mathvariant=¨bold¨ displaystyle=¨false¨»«mfrac»«mi»m«/mi»«msup»«mi»s«/mi»«mn»2«/mn»«/msup»«/mfrac»«/mstyle»«/menclose»«/mstyle»«/math»
نحسب ازاحة الحركة في المرحلة الثالثة من المساحة المحصورة ، قسّم المساحة إلى مثلثين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1608;§#1580;§#1576;§#1577;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1587;§#1575;§#1581;§#1577;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1605;§#1602;§#1583;§#1575;§#1585;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»x«/mi»«msub»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»4«/mn»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1587;§#1575;§#1604;§#1576;§#1577;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1587;§#1575;§#1581;§#1577;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1605;§#1602;§#1583;§#1575;§#1585;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»x«/mi»«msub»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mstyle»«/math»
في المجموع في المرحلة الثالثة، تكون الإزاحة صفر متر.
- في المرحلة الرابعة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math» يتحرك الجسم بسرعة ثابتة.
نحسب ازاحة الحركة في المرحلة الرابعة، من المساحة المحصورة :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1587;§#1575;§#1581;§#1577;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»x«/mi»«mn mathvariant=¨bold¨»4«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mstyle»«/math»
-في المرحلة الخامسة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math» الجسم يتحرك بتسارع موجب وثابت.
نحسب تسارع الجسم في مرحلة الحركة الخامسة، من ميل الدالة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1587;§#1575;§#1581;§#1577;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»v«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»(«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»8«/mn»«mn mathvariant=¨bold¨»1«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨ displaystyle=¨false¨»«mfrac»«mi»m«/mi»«msup»«mi»s«/mi»«mn»2«/mn»«/msup»«/mfrac»«/mstyle»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»a«/mi»«mn mathvariant=¨bold¨»5«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»8«/mn»«mstyle mathvariant=¨bold¨ displaystyle=¨false¨»«mfrac»«mi»m«/mi»«msup»«mi»s«/mi»«mn»2«/mn»«/msup»«/mfrac»«/mstyle»«/menclose»«/mstyle»«/math»
نحسب ازاحة الحركة في مقطع الحركة الخامس من المساحة المحصورة في الثواني الثلاث الأولى:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1587;§#1575;§#1581;§#1577;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»x«/mi»«mn mathvariant=¨bold¨»5«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»4«/mn»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mstyle»«/math»
بعد التوقف اللحظي، يتحرك الجسم عكس اتجاه المحور في ثلاث حركات مختلفة: تسارع سلبي ، وسرعة ثابتة ، وتسارع موجب. ازاحة الجسم خلال هذه الثواني الثلاث هي 16 مترًا ، عكس اتجاه المحور. الإزاحة الكلية لحركة الجسم خلال الـ 9 ثوانٍ هي 16 مترًا.
9.ب- الرسم البياني X(t),خمس حركات مختلفة.
الرسم البياني المعطى هو رسم بياني للموقع كدالة للزمن.
في الرسم البياني للموقع كدالة للزمن، يكون ميل الدالة الموصوفة مساويًا لسرعة الجسم.
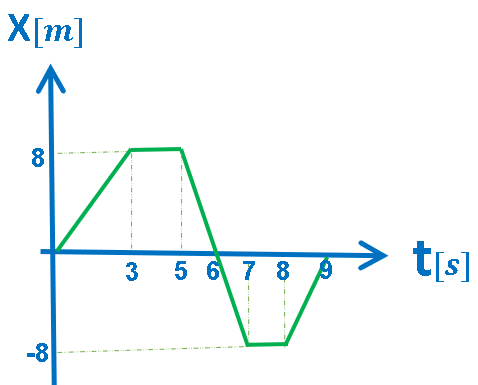
رياضيًا، يصف الرسم البياني خمس دوال مختلفة:
الدالة الأولى, بالفترة الزمنية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mn mathvariant=¨bold¨»3«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»: دالة خطية تصاعدية.
الدالة الثانية, بالفترة الزمنية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»3«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»: دالة ثابتة مقدارها 8 أمتار.
الدالة الثالثة, بالفترة الزمنية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»5«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mn mathvariant=¨bold¨»7«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»: دالة خطية تنازلية.
الدالة الرابعة, بالفترة الزمنية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»7«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mn mathvariant=¨bold¨»8«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»: دالة ثابتة مقدارها 8- أمتار .
الدالة الخامسة, بالفترة الزمنية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»8«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mn mathvariant=¨bold¨»9«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»: دالة خطية تصاعدية.
الرسم البياني يصف خمس مراحل للحركة.
- في المرحلة الأولى من الحركة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math» يتحرك الجسم بسرعة موجبة وثابتة (باتجاه المحور).
نحسب سرعة الجسم في مرحلة الحركة الأولى «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math»، من ميل الدالة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»66«/mn»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨ displaystyle=¨false¨»«mfrac»«mi»m«/mi»«mi»s«/mi»«/mfrac»«/mstyle»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»66«/mn»«mstyle mathvariant=¨bold¨ displaystyle=¨false¨»«mfrac»«mi»m«/mi»«mi»s«/mi»«/mfrac»«/mstyle»«/menclose»«/mstyle»«/math»
في المرحلة الثانية للحركة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math», الجسم في حالة سكون بالموقع X=8m.
في المرحة الثالثة للحركة، يتحرك الجسم بسرعة سالبة ثابتة (عكس اتجاه المحور).
احسب سرعة الجسم في مقطع الحركة الثالث «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math»، من ميل الدالة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»7«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»16«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨ displaystyle=¨false¨»«mfrac»«mi»m«/mi»«mi»s«/mi»«/mfrac»«/mstyle»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«mstyle mathvariant=¨bold¨ displaystyle=¨false¨»«mfrac»«mi»m«/mi»«mi»s«/mi»«/mfrac»«/mstyle»«/menclose»«/mstyle»«/math»
في المرحلة الرابعة للحركة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math»، الجسم ساكن بالموقع X= - 8m.
في المرحلة الخامسة للحركة يتحرك الجسم بسرعة موجبة ثابتة (في اتجاه المحور).
نحسب سرعة الجسم في المرحلة الخامسة للحركة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#60;«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math»، من ميل الدالة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»(«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»8«/mn»«mn mathvariant=¨bold¨»1«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨ displaystyle=¨false¨»«mfrac»«mi»m«/mi»«mi»s«/mi»«/mfrac»«/mstyle»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»5«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»8«/mn»«mstyle mathvariant=¨bold¨ displaystyle=¨false¨»«mfrac»«mi»m«/mi»«mi»s«/mi»«/mfrac»«/mstyle»«/menclose»«/mstyle»«/math»
خلاصة: يتحرك الجسم من نقطة أصل المحور بسرعة ثابتة لمدة 3 ثوانٍ حتى الموقع X=8m، ويستقر الجسم في هذا الموقع لمدة ثانيتين حتى اللحظة t = 5s.
من اللحظة t = 5s يتحرك الجسم لمدة ثانيتين بسرعة سالبة ثابتة حتى الموقع X = -8m ، يستقر الجسم في هذا الموقع لمدة ثانية واحدة حتى اللحظة t = 8s.
من اللحظة t = 8s يتحرك الجسم بسرعة ثابتة في اتجاه المحور حتى يعود الجسم إلى نقطة بداية المحور.
10.أ- الرسم البياني V(t), حركة بتسارع متغير.
الرسم البياني المعطى هو رسم بياني للسرعة كدالة للزمن.
في الرسم البياني للسرعة كدالة للزمن، يكون ميل الدالة الموصوفة في الرسم البياني مساويًا لتسارع الجسم، والمساحة المحصورة بين الدالة ومحور الزمن تساوي ازاحة الحركة.
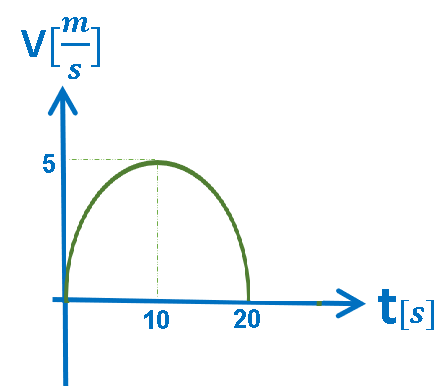
رياضيا ، الرسم البياني يصف قطع مكافئ.
في بداية الحركة، يكون ميل الدالة موجبًا، ويأخذ الميل بالنقصان كل زمن الحركة.
يتحرك الجسم بتسارع متغير. تسارعه الأولي موجب، التسارع يقل خلال الحركة.
خلاصة: يتحرك الجسم لمدة 20 ثانية في اتجاه المحور، ويبدأ الجسم في التحرك من حالة السكون بتسارع كبير.
تسارع الجسم يتناقص خلال الحركة.
في اللحظة t = 10s ، تسارع الجسم يساوي صفرًا ، ويبدو من الرسم البياني أن سرعته في هذه اللحظة هي 5 أمتار لكل ثانية.
10.ب- الرسم البياني X(t),حركة بسرعة متغيرة.
الرسم البياني المعطى هو رسم بياني للموقع كدالة للزمن.
في الرسم البياني للموقع كدالة للزمن، يكون ميل الدالة الموصوفة مساويًا لسرعة الجسم.
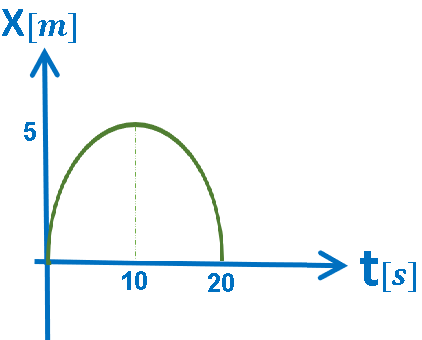
رياضيًا ، يصف الرسم البياني قطع مكافئ "باكية"
ميل الدالة آخذ بالنقصان خلال كل فترة الحركة، وبالتالي تقل السرعة طوال زمن الحركة.
خلاصة: يتحرك الجسم من نقطة بداية المحور بسرعة موجبة متناقصة (تسارع سالب) ، في نهاية الحركة يعود الجسم إلى نقطة الأصل.
في أول 10 ثوانٍ ، يتحرك الجسم في اتجاه المحور، وفي آخر 10 ثوانٍ يتحرك الجسم عكس اتجاه المحور.
11.أ- الرسم البياني X(t),حركة بسرعة متغيرة.
الرسم البياني المعطى هو رسم بياني للموقع كدالة للزمن.
في الرسم البياني للموقع كدالة للزمن، يكون ميل الدالة الموصوفة مساويًا لسرعة الجسم.
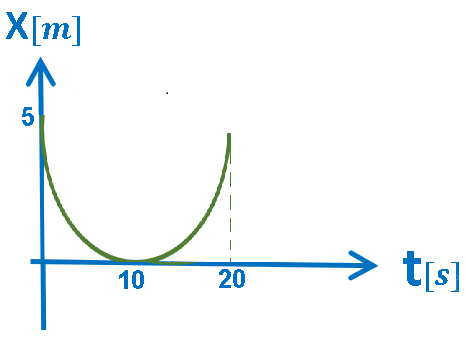
رياضيًا ، يصف الرسم البياني قطع مكافئ "ضاحك".
في بداية الحركة، يكون ميل الدالة سالبًا، ويزداد الميل طوال الحركة.
يتحرك الجسم بسرعة متغيرة. سرعته البدائية سالبة، وتزداد السرعة خلال الحركة.
خلاصة: يبدأ الجسم في التحرك من الموقع X=5m بسرعة ابتدائية سالبة. تزداد سرعته طوال وقت حركته، مما يعني أن الجسم يتحرك بتسارع موجب. نظرًا لأن شكل الدالة عبارة عن قطع مكافئ، فيمكن القول أن الجسم يتحرك بتسارع موجب وثابت.
في اللحظة t = 10s ، عجلة السرعة تساوي صفرًا ، ويبدو من الرسم البياني أن موقع الجسم في هذه اللحظة يساوي صفرًا.
11.ب- الرسم البياني V(t), حركة بتسارع متغير.
الرسم البياني المعطى هو رسم بياني للسرعة كدالة للزمن.
في الرسم البياني للسرعة كدالة للزمن، يكون ميل الدالة الموصوفة في الرسم البياني مساويًا لتسارع الجسم، والمساحة المحصورة بين الدالة ومحور الزمن تساوي ازاحة الحركة.
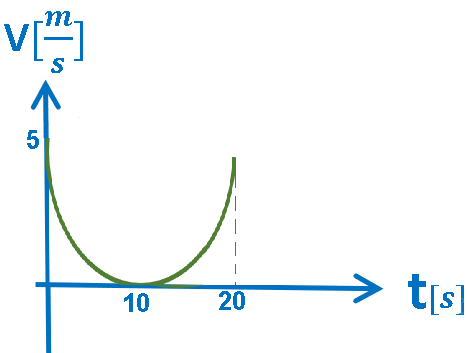
رياضيًا ، يصف الرسم البياني قطع مكافئ "ضاحك".
في بداية الحركة، يكون ميل الدالة سالبًا، ويزداد الميل طوال الحركة.
يتحرك الجسم بتسارع متغير. تسارعها الابتدائي سالب، التسارع يزداد طوال الحركة .
خلاصة: يتحرك الجسم لمدة 20 ثانية في اتجاه المحور، وسرعته الابتدائية 5 أمتار في الثانية، يتحرك الجسم بتسارع سالب في لحظة بدء حركته.
تسارع الجسم يزداد خلال الحركة.
في اللحظة t = 10s، يكون تساترع الجسم صفرًا، ومن الرسم البياني نلاحظ أن سرعته في هذه اللحظة تساوي صفرًا.