______________________________________________________________________________________
...
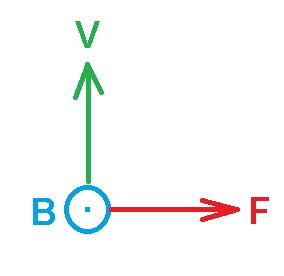
اتجاه الحقل المغناطيسي يخرج من الصفحة حسب قاعدة اليد اليسرى.
قاعدة اليد اليسرى.
أيون الهيدروجين وأيون الهيليوم مشحونان بشحنة موجبة، فعندما تكون الأيونات في النقطة A تؤثر عليهما قوة إلى اليمين حسب اتجاه حركتهما وحسب قاعدة اليد اليسرى ينتج أنّ اتجاه الحقل المغناطيسي نحو الخارج.
1. وفقًا لاتجاه حركة الشحنة يمكن معرفة اتجاه القوة المغناطيسية المؤثرة عليها.
2. لتحديد اتجاه الحقل المغناطيسي، نستخدم قاعدة اليد اليسرى في نقطة واحدة في مسار حركة الشحنة.
3. عادة يكون مُعطى اتجاه الحقل واتجاه الحركة ويُطلب تحديد اتجاه القوة المغناطيسية وفقا لذلك ويتم تحديد الاتجاه باستخدام قاعدة اليد اليسرى.
في هذه الحالة يجب معرفة اتجاه الحقل المغناطيسي،من المفروض أن يكون اتجاه الحقل ربما يكون داخل الصفحة أو خارجها،
ونتحقق باستخدام قاعدة اليد اليسرى لكل خيار من الخيارين.
2. כדי למצוא את כיוון השדה המגנטי יש להשתמש בכלל יד שמאל בנקודה אחת במסלול תנועת המטען.
3. בדרך כלל, נתון כיוון השדה וכיוון התנועה ויש למצוא את כיוון הכוח המגנטי בהתאם בעזרת כלל יד שמאל.
במקרה זה יש למצוא את כיוון השדה המגנטי , מומלץ להניח שכיוון השדה הוא ככל הנראה לתוך הדף או אל מחוץ הדף,
ולבדוק עם כלל יד שמאל כל אחת משתי האפשרויות.
______________________________________________________________________________________
______________________________________________________________________________________
...
لا تتغير السرعة لأن القوة المغناطيسية تعمل بشكل عمودي على الحركة.
قانون الشغل والطاقة أو الديناميكا.
تعمل القوة المغناطيسية باتجاه عمودي على الحركة، من تعريف الشغل: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»c«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»o«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math» , الشغل الذي تبذله القوة المغناطيسية يساوي صفرًا.
من قانون الشغل والطاقة: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathcolor=¨#0000FF¨ mathvariant=¨bold¨»K«/mi»«/msub»«/math» , نظرًا لعدم بذل أي شغل، لا يحدث أي تغيير في الطاقة الحركية.
وبالتالي فإن مقدار السرعة لا يتغير.
ממשפט העבודה אנרגיה: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathcolor=¨#0000FF¨ mathvariant=¨bold¨»K«/mi»«/msub»«/math» , מכיוון שלא מבוצעת עבודה אין שינוי באנרגיה הקינטית.
מכאן שהמהירות לא משתנה בגודלה.
1. لا يتغير مقدار السرعة ولكن اتجاهها يتغير.
2. يمكن أيضًا الإجابة على السؤال من مبادئ الديناميكا. تعمل القوة المغناطيسية دائمًا بشكل عمودي على الحركة، وليس لها أي مركّب في اتجاه الحركة
أو في الاتجاه المعاكس للحركة فلا يؤثر على مقدار السرعة. إنه يؤثر فقط على اتجاه الحركة.
3. تعمل القوة المغناطيسية دائمًا في اتجاه عمودي على الحركة، وبالتالي فهي تتحرك في حركة دائرية منتظمة.
4. القوة الجاذبة المركزية لا تبذل شغل لأنها متعامدة للحركة، وبالتالي لا يتم بذل طاقة، وهكذا تتحرك الأجسام السماوية دون استثمار طاقة.
وبالمثل، يتحرك الإلكترون أيضًا في حركة كوكبية حول البروتون.
2. אפשר לענות על השאלה גם מעקרונות הדינמיקה. הכוח המגנטי פועל תמיד בניצב לתנועה אין לו רכיב בכיוון התנועה
או בכיוון הנגדי לתנועה, לכן הוא לא משפיע על גודל המהירות. הוא משפיע רק על כיוון התנועה.
3. הכוח המגנטי תמיד פועל בכיוון ניצב לתנועה, לכן הוא תמיד גורם לתנועה מעגלית קצובה.
______________________________________________________________________________________

______________________________________________________________________________________
...
زمن حركة أيون الهيدروجين هو: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«/math»
التعبير عن زمن الدورة لشحنة تتحرك في حركة دائرية.
زمن حركة أيون الهيدروجين في الحقل المغناطيسي يساوي نصف زمن الدورة. نًطوِّر تعبيرًا لزمن الدورة:
نرسم مخططًا للقوى التي تعمل على أيون الهيدروجين عند مروره بالنقطة A:
نكتب معادلة القوى:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»
تتحرك الكرة في مستوى عمودي على الحقل المغناطيسي ولذلك: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/math», نعبر عن زمن الدورة من معادلة الحركة الجاذبة المركزية.
ونعبر عن السرعة الخطية كدالة للسرعة الزاوية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»90«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»§#969;«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»
يتحرك أيون الهيدروجين لمدة زمنية نصف دورة، نحسب زمن حركة أيون الهيدروجين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«/math»
وبالتالي فإن التعبير لزمن حركة أيون الهيدروجين هو: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«/math»
נערוך תרשים כוחות ליון המימן כאשר הוא חולף בנקודה A:
נכתוב את משוואת התנועה :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»
הכדור נע במישור הניצב לשדה המגנטי לכן «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/math», נבטא את זמן המחזור ממשוואת התנועה הצנטריפטאלית.
נבטא את המהירות הקווית בתלות במהירות הזוויתית:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»90«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»§#969;«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»
יון המימן נע במשך חצי זמן מחזור, נחשב את זמן תנועת יון המימן:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«/math»
לכן, ביטוי זמן תנועת יון המימן הוא:
1. يجب أن يُفهم من الرسم البياني أن زمن حركة أيون الهيدروجين هو نصف زمن الدورة.
2. حركة أيون الهيدروجين لا تتعلق على حركة أيون الهيليوم .
2. תנועת יון המימן איננה תלויה בתנועת יון ההליום.
______________________________________________________________________________________
ج. 
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»4«/mn»«/math»
التعبير عن زمن الدورة.
نعبر عن النسبة بين زمن حركة أيون الهيليوم وزمن حركة أيون الهيدروجين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»t«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»t«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle displaystyle=¨true¨»«mfrac»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«menclose notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/mfrac»«/mstyle»«mstyle displaystyle=¨true¨»«mfrac»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«menclose notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/mfrac»«/mstyle»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle displaystyle=¨true¨ mathvariant=¨bold¨»«msub»«mi»T«/mi»«mi»HE«/mi»«/msub»«/mstyle»«mstyle displaystyle=¨true¨ mathvariant=¨bold¨»«msub»«mi»T«/mi»«mi»H«/mi»«/msub»«/mstyle»«/mfrac»«/math»
النسبة بين زمني حركة الأيونين تساوي النسبة بين زمني الدورة، نجد هذه النسبة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle displaystyle=¨true¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«/mrow»«/mfrac»«/mstyle»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«/mfrac»«/math»
شحنة الهيليوم وشحنة الهيدروجين متساويتان في المقدار، وكتلة الهيليوم أكبر بأربع مرات من كتلة الهيدروجين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle displaystyle=¨true¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«/mrow»«/mfrac»«/mstyle»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle mathvariant=¨bold¨ displaystyle=¨true¨»«mfrac»«mrow»«menclose notation=¨horizontalstrike¨»«mn»2«/mn»«mo»§#183;«/mo»«mi»§#960;«/mi»«/menclose»«mo»§#183;«/mo»«mn»4«/mn»«mo»§#183;«/mo»«msub»«mi»m«/mi»«mi»H«/mi»«/msub»«/mrow»«menclose notation=¨downdiagonalstrike¨»«mi»B«/mi»«mo»§#183;«/mo»«msub»«mi»q«/mi»«mi»H«/mi»«/msub»«/menclose»«/mfrac»«/mstyle»«mfrac»«mrow»«menclose notation=¨horizontalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/menclose»«/mfrac»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«/math»
زمن حركة أيون الهيليوم أكبر بأربع مرات من زمن حركة أيون الهيدروجين.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«mi mathvariant=¨bold¨»TH«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle displaystyle=¨true¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«/mrow»«/mfrac»«/mstyle»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«/mfrac»«/math»
מטען ההליום ומטען המימן זהים בגודלם, מסת ההליום גדולה פי 4 ממסת המימן:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«mi mathvariant=¨bold¨»TH«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle displaystyle=¨true¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«/mrow»«/mfrac»«/mstyle»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle displaystyle=¨true¨ mathvariant=¨bold¨»«mfrac»«mrow»«menclose notation=¨horizontalstrike¨»«mn»2«/mn»«mo»§#183;«/mo»«mi»§#960;«/mi»«/menclose»«mo»§#183;«/mo»«mn»4«/mn»«mo»§#183;«/mo»«msub»«mi»m«/mi»«mi»H«/mi»«/msub»«/mrow»«menclose notation=¨downdiagonalstrike¨»«mi»B«/mi»«mo»§#183;«/mo»«msub»«mi»q«/mi»«mi»H«/mi»«/msub»«/menclose»«/mfrac»«/mstyle»«mfrac»«mrow»«menclose notation=¨horizontalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/menclose»«/mfrac»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«/math»
זמן תנועת יון ההליום גדול פי 4 מזמן תנועת יון המימן.
1. الأيونات متشابهة في شحنتها ولكنها تختلف في كتلتها. من التعبير عن زمن الدورة لشحنة تتحرك في حقل مغناطيسي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«/math»
من التعبير يمكن أن نرى أن زمن الدورة يتناسب طرديًا مع الكتلة. كتلة أيون الهيليوم أكبر بأربع مرات من كتلة أيون الهيدروجين. ولذلك فإن زمن دورة أيون الهيليوم أكبر بأربع مرات، وزمن حركته أكبر بأربع مرات.
2. السؤال يتعلق بالنسبة بين زمني حركة الأيونات وليس بالنسبة بين زمني الدورة.
قبل استخدام تعبير زمن الدورة، يجب توضيح أن النسبة بين زمني حركة الأيونات تساوي النسبة بين زمني الدورة.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«/math»
מהביטוי ניתן לראות שזמן המחזור תלוי ביחס ישר במסה . ליון ההליום מסה גדולה פי 4 ממסת יון המימן . לכן זמן המחזור של יון ההליום גדול פי 4. וזמן תנועתו גדול פי 4.
2. השאלה היא על יחס זמני תנועת היונים, ולא על יחס זמני המחזור .
לפני שמשתמשים בביטוי זמן המחזור יש להראות שיחס זמני תנועת היונים שווה ליחס זמני המחזור.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»d«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»2«/mn»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«/msqrt»«/math»
البعد d يساوي الفرق بين قطري المسارين.
يمكن التعبير عن قطر كل مسار باستخدام تعبير نصف قطر مسار شحنة تتحرك في حقل مغناطيسي.
ניתן לבטא את הקוטר של כל מסלול בעזרת ביטוי לרדיוס המסלול של מטען הנע בשדה מגנטי.
البعد d يساوي الفرق بين قطري المسارين، نعبر عن البعد بدلالة نصفي قطري المسارين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»HE«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»H«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/math»
نعبر عن نصف قطر المدار من معادلة الحركة الدائرية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
تتحرك الشحنة بشكل عمودي على الحقل، والزاوية α تساوي 90 درجة. التعبير عن نصف قطر المسار:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»V«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»90«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«menclose notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
نعبر عن البعد d باستخدام تعبير نصف قطر مسار حركة الأيون:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/math»
يجب التعبير عن البعد d بدلالة فرق الجهد وليس بدلالة السرعة d .
للتمييز بين السرعة وفرق الجهد، نُشير إلى السرعة بالحرف V وفرق الجهد بـ - «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/math».
نستخدم قانون الشغل والطاقة للتعبير عن سرعة الأيونات بعد تسريعهما:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/menclose»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨/»«/math»
نعوِّض سرعة الأيونات بدلالة توتر التسريع، بتعبير البعد d:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«/mfrac»«/msqrt»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mfrac»«/msqrt»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
مُعطى: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»HE«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»H«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»,«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»HE«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»H«/mi»«/msub»«/math» , نعوِّض في تعبير البعد d:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mfrac»«/msqrt»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
تبسيط جبري:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mfrac»«/msqrt»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»8«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«msqrt»«mfrac»«mrow»«msup»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«menclose notation=¨downdiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«menclose notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«menclose notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«msqrt»«mfrac»«mrow»«msup»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«menclose notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨horizontalstrike¨»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«menclose notation=¨horizontalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»d«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»2«/mn»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«/msqrt»«/menclose»«/math»
ولذلك، فإن التعبير البعد بين نقطتي إصابة الأيونين هو: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«/msqrt»«/math»
1. من المتبع الإشارة لفرق الجهد (التوتر) بـ «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«/math» أو U , في السؤال، يشار إلى التوتر بالحرف V مثل السرعة من المهم جدًا استخدام رموز مختلفة
للسرعة وفرق الجهد. بالنسبة لأولئك الذين اعتادوا على استخدام الإشارة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«/math» من المفضل أن نُشير لفرق الجهد بـ «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«/math» على الرغم من أنه أشير له في نص السؤال بـ V.
2. الخطوة الجبرية في هذا السؤال طويلة ومرهقة بعض الشيء، إذا لم يتبقى الكثير من الوقت في الامتحان، فمن المستحسن عدم التبسيط جبريا.
يمكنك كتابة التعبير بدلالة المقادير الأربعة التي تظهر في السؤال والتوقف عند هذه المرحلة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mrow mathcolor=¨#FF0000¨»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»v«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»v«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mfrac»«/msqrt»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
3. من الممكن التوصل إلى تعبير السرعة V للشحنة المتسارعة ببدلالة فارق الجهد «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«/math» , حسب حفظ الطاقة الكلية:
نُشير إلى النقطة التي بدأت فيها الشحنة بالتسارع بـ O ونقطة نهاية التسارع بـ A:
دعونا نشير إلى الطاقة الوضعية بـ U، والفرق بالطاقة الوضعية بـ«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»OA«/mi»«/msub»«/math».
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»O«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#FF0000¨ notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«msub»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»O«/mi»«/msub»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»O«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»O«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»q«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»q«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#FF0000¨ notation=¨circle¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/msqrt»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»
למהירות ולמתח. למי שרגיל להשתמש בסימון U למתח מומלץ לסמן את המתח באות U למרות שהמתח מסומן באות V.
2. המהלך האלגברי בשאלה זו מעט ארוך ומסורבל , אם לא נשאר הרבה זמן בבחינה, מומלץ לא לפשט אלגברית.
רק לכתוב את הביטוי בתלות בארבעת הגדלים המופיעים בשאלה.
______________________________________________________________________________________