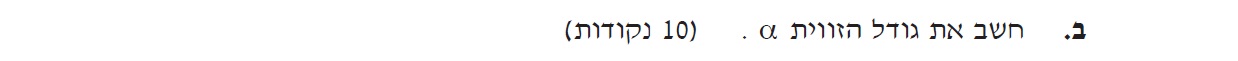الحلول والمنتديات لـ"ألبوم الحلول" في موضوع الحقل المغناطيسي
| الموقع: | YouCube |
| المقرر: | שדה מגנטי - ערבית |
| كتاب: | الحلول والمنتديات لـ"ألبوم الحلول" في موضوع الحقل المغناطيسي |
| طبع بواسطة: | משתמש אורח |
| التاريخ: | الأربعاء، 4 فبراير 2026، 2:32 AM |
جدول المحتويات
- 1. 2016,4-إيجاد المركب الأفقي للحقل المغناطيسي للكرة الأرضية، بواسطة ملف دائري رفيع
- 2. 2014,5- مصفاة السرعة ومطياف الكتل
- 3. 2013,4 - إيجاد المركب الأفقي للحقل المغناطيسي الأرضي بواسطة لسلك مستقيم
- 4. 2011,4- تتسارع أيونات داخل حقل كهربائي وتدخل إلى المطياف
- 5. 2010,4- تتحرك كرة مشحونة داخل حقل مغناطيسي
- 6. 2010,5- الحقل المغناطيسي حول سلك مستقيم
- 7. 2008,4- تتحرك شحنة في أربع مناطق مُربعة الشكل
- 8. 2007,4- شحنة تتحرك في حقل كهربائي وحقل مغناطيسي EK
- 9. 2007,5- ايجاد المركب الأفقي للحقل المغناطيسي الأرضي بواسطة ملف طويلة
1. 2016,4-إيجاد المركب الأفقي للحقل المغناطيسي للكرة الأرضية، بواسطة ملف دائري رفيع
______________________________________________________________________________________
...
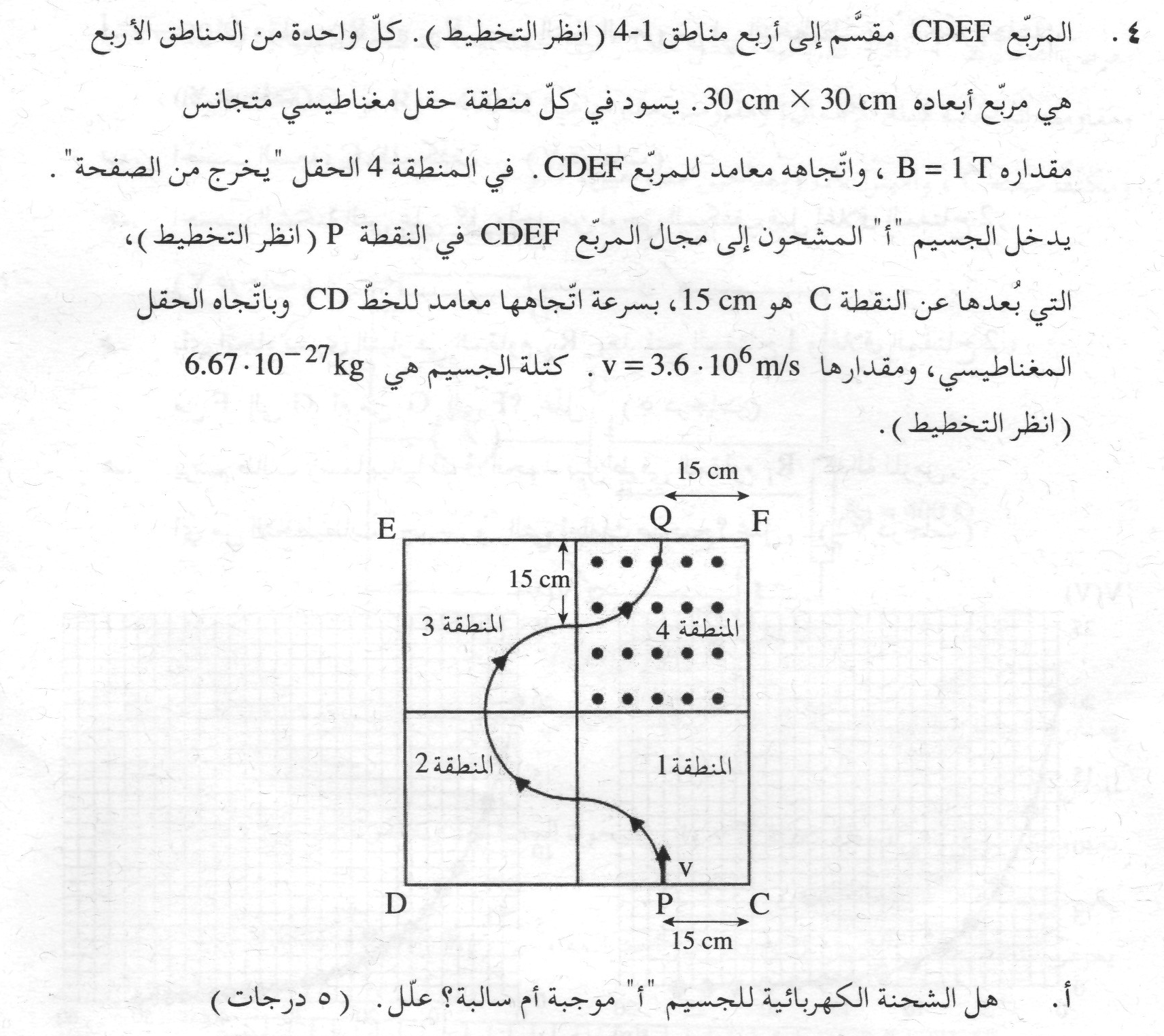
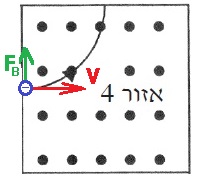
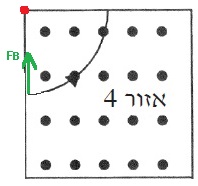
القطب K موجب. لكي تستقر الإبرة في الاتجاه الأفقي، يجب أن يخرج التيار من القطب K.
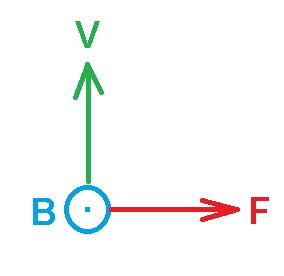
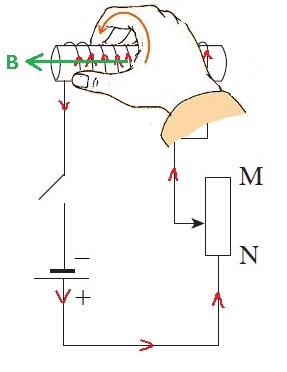
قاعدة اليد اليمنى. في كل بطارية، يتدفق التيار في الدائرة من القطب الموجب نحو القطب السالب.
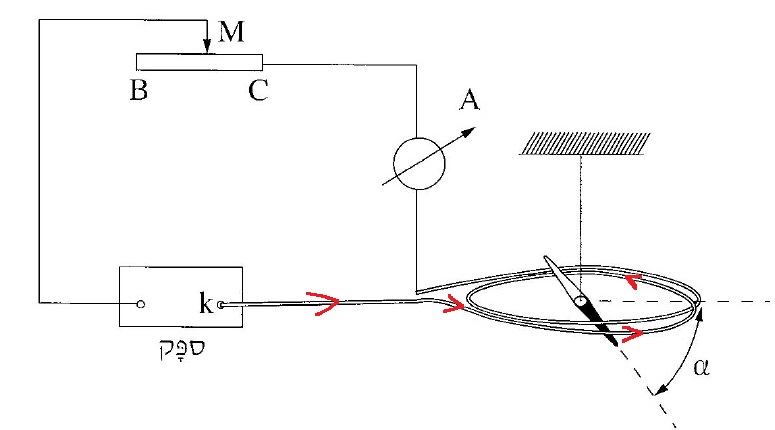
لكي تستقر الإبرة في الاتجاه الأفقي، يجب أن يكون اتجاه الحقل المغناطيسي الناتج عن الملف الدقيق لأعلى.
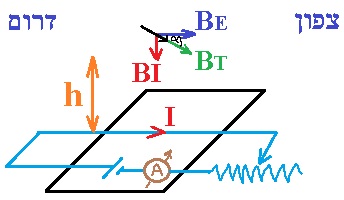
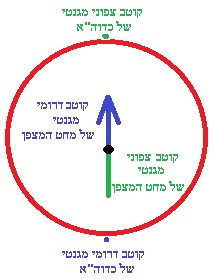
نرسم رسم تخطيطي للحقول المغناطيسية:
حسب قاعدة اليد اليمنى، لكي يعمل الحقل المغناطيسي للأعلى، يجب أن يكون اتجاه التيار في القطب القريب للملف إلى اليمين.
كما هو مبين في الشكل التالي:
يخرج التيار من القطب K، لذا فإن القطب K موجب.
מכלל יד ימין
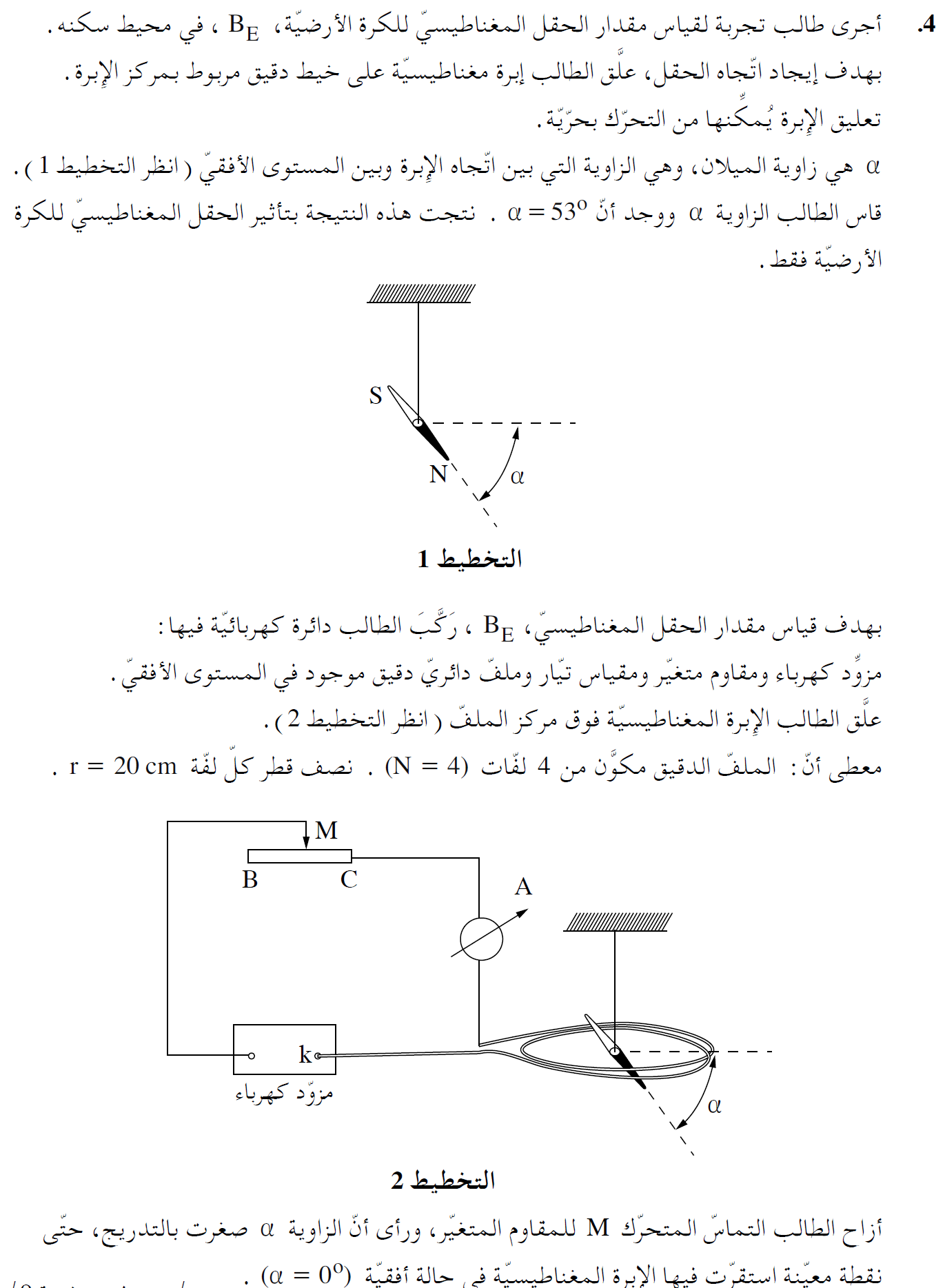
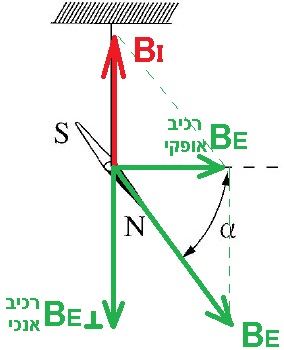
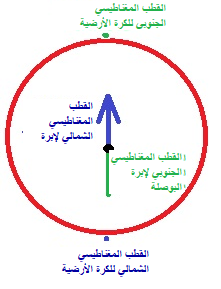
1. اتجاه إبرة البوصلة قبل تدفق التيار في الملف، هو اتجاه الحقل المغناطيسي للأرض.
اتجاه الحقل المغناطيسي الناتج عن الملف الدقيق هو للأعلى، وتستقر الإبرة في اتجاه متّجه الحقل المغناطيسي المحصّل
للحقل المغناطيسي للأرض، والحقل المغناطيسي الناتج عن التيار.
لفهم بنود الأسئلة وعمل الدائرة، من المهم رسم رسمًا تخطيطيًا يحتوي جميع الحقول المغناطيسية.
2. يجب الإجابة على السؤال حسب الشكل الذي يتم فيه لف الملف الدقيق في الشكل.
3. اتجاه التيار الحقيقي عكس الاتجاه المتفق عليه ولكن لا نستخدم قاعدة اليد اليمنى ونحدد الجهد الموجب في الاتجاه الصحيح فقط في الاتجاه المتفق عليه.
כיוון שדה המגנטי הנוצר מהסליל הדק הוא כלפי מעלה, המחט מתייצבת בכיוון ווקטור השדה המגנטי השקול
לשדה המגנטי של כדור הארץ, ולשדה המגנטי שנוצר מהזרם.
כדי להבין את סעיפי השאלות ואת פעולת המעגל חשוב לערוך תרשים המכיל את כל השדות המגנטיים.
2. יש לענות על השאלה בהתאם לצורה שבה הסליל הדק כרוך באיור.
3. כיוון הזרם האמתי הפוך לכיוון המוסכם, אך אנחנו לא משתמשים בכלל יד ימין ובקביעת הפוטנציאל החיובי בכיוון האמתי
רק בכיוון המוסכם.
______________________________________________________________________________________
______________________________________________________________________________________
...
قام الطالب بنقل التماسّ المتحرك من النقطة B إلى النقطة C. وبالتالي تقل المقاومة المحصّلة ويزداد التيار وتزداد شدة الحقل المغناطيسي.
التعبير عن شدة الحقل المغناطيسي في مركز ملف دائري رفيع، قانون أوم، ومعرفة المقاومة المتغيرة.
الزاوية α تصبح أصغر، وبالتالي فإن الحقل المغناطيسي الناتج عن الملف الدقيق يصبح أكبر.
من التعبير عن شدة الحقل المغناطيسي في وسط الملف الدقيق:«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«/mstyle»«/math» , شدة الحقل المغناطيسي في وسط الملف يتناسب طرديا مع التيار.
لكي يزداد الحقل المغناطيسي، يجب زيادة التيار في الدائرة، من قانون أوم لزيادة التيار يجب تقليل المقاومة المحصّلة ،
ولذلك قام الطالب بتحريك التماسّ المتحرك M باتجاه النقطة C.
מביטוי עוצמת השדה המגנטי במרכז הסליל ההדק: «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«/mstyle»«/math» , השדה המגנטי במרכז הכריכה תלוי ביחס ישר בזרם.
כדי השדה המגנטי ילך ויגדל יש להגדיל את עוצמת הזרם במעגל, מחוק אום כדי שהזרם יגדל ההתנגדות השקולה צריכה לקטון,
לכן , התלמיד הזיז את הגררה M לכיוון הנקודה .
1. يعتمد الحل على سلسلة من الخطوات المرتبطة ببعضها البعض.
لحل السؤال بشكل صحيح، من المهم أن نفهم تمامًا كل خطوة من الخطوات والعلاقة بين الخطوات.
2. تعبير الحقل المغناطيسي: «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«/mstyle»«/math» يناسب فقط للنقاط في مركز الملف. يجب التعامل مع الإبرة المغناطيسية كجسم يتأثر من الحقل المغناطيسي بمركز الملف.
כדי לפתור את השאלה בצורה נכונה, חשוב להבין היטב כל אחד מהשלבים ואת הקשר בין שלב לשלב.
2. ביטוי השדה המגנטי: «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«/mstyle»«/math» מתאים רק לנקודת מרכז הסליל. יש להתייחס למחט המגנטית כאל גוף המושפע
מהשדות המגנטיים במרכז הסליל.
______________________________________________________________________________________
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»B«/mi»«mrow»«mi mathsize=¨20px¨ mathvariant=¨bold¨»E«/mi»«mo mathsize=¨20px¨ mathvariant=¨bold¨»§#8869;«/mo»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathsize=¨20px¨»=«/mo»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»4«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»02«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathsize=¨20px¨»10«/mn»«mrow»«mo mathsize=¨20px¨ mathvariant=¨bold¨»-«/mo»«mn mathsize=¨20px¨ mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathsize=¨20px¨»T«/mi»«/math»
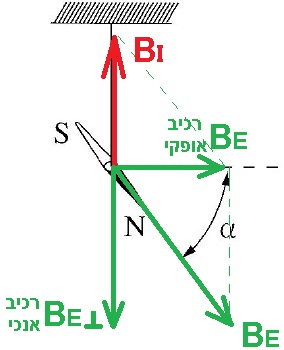
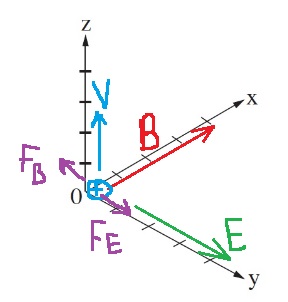
تعبير الحقل المغناطيسي في وسط ملف دائري دقيق. في الاتجاه العمودي تكون محصّلة الحقول مساوية صفر.
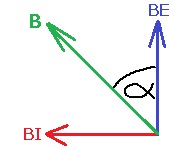
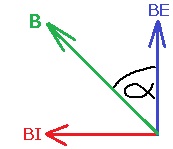
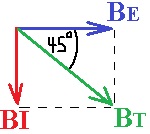
وفقًا لمخطط الحقول المغناطيسية، عندما تستقر الإبرة في الاتجاه الأفقي، فإن مركَّب الحقل المغناطيسي العمودي يساوي مقدار الحقل المغناطيسي الناتج من التيار:
يتحقق أنّ: «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8869;«/mo»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»BI«/mi»«/mrow»«/mstyle»«/math»
نستخدم تعبير الحقل المغناطيسي في وسط ملف دائري رفيع:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8869;«/mo»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»02«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/mstyle»«/math»
وبالتالي فإن مقدار المركّب العمودي للحقل المغناطيسي هو: «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»02«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/mstyle»«/math»
מתקיים: «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8869;«/mo»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»BI«/mi»«/mrow»«/mstyle»«/math»
נשתמש בביטוי השדה מגנטי במרכז סליל מעגלי דק:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8869;«/mo»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»02«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/mstyle»«/math»
לכן, גודלו של הרכיב האנכי של הכוח המגנטי גודלו: «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»02«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/mstyle»«/math»
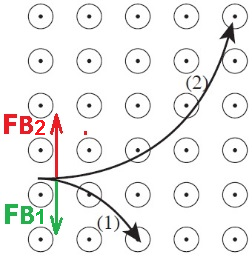
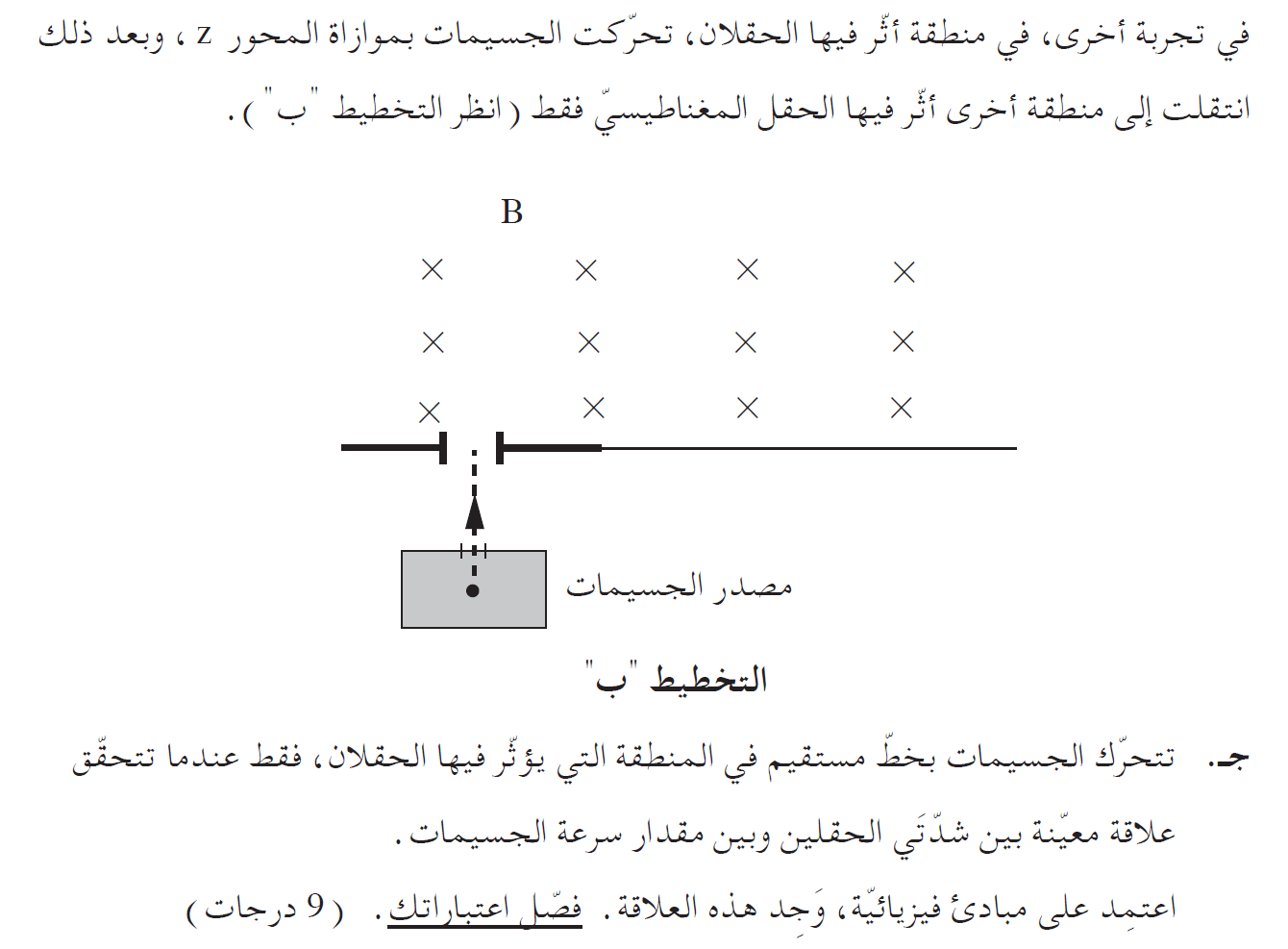
1. في الرسم البياني 2 يمكنك أن ترى أن هناك لفتين في الملف الدقيق. يشير الخط الموجود أعلى الرسم التخطيطي إلى وجود 4 لفات في الملف.
بشكل عام الرسم التوضيحي للتوضيح فقط، إذا كان هناك تناقض بين النص والرسم فالنص هو الذي يحسم وليس الرسم.
2. في كل قياس توجد أخطاء قياس عشوائية، ومن أجل تقليل أخطاء القياس يجب إجراء عملية حساب متوسط للأخطاء العشوائية.
لذلك، ليس من الصحيح استخلاص نتيجة من قياس واحد. لإيجاد المركَّب العمودي للحقل المغناطيسي يجب إجراء عدة قياسات.
באופן כללי האיור הוא להמחשה בלבד, אם יש סתירה בין המלל לאיור המלל הוא הקובע ולא האיור.
2. בכל מדידה קיימות שגיאות מדידה אקראיות, כדי לצמצם את שגיאות המדידה יש לבצע פעולת מיצוע לשגיאות האקראיות.
לכן, לא נכון להגיע למסקנה ממדידה אחת. כדי למצוא את הרכיב האנכי של השדה המגנטי יש לבצע מספר מדידות.
______________________________________________________________________________________
______________________________________________________________________________________
...
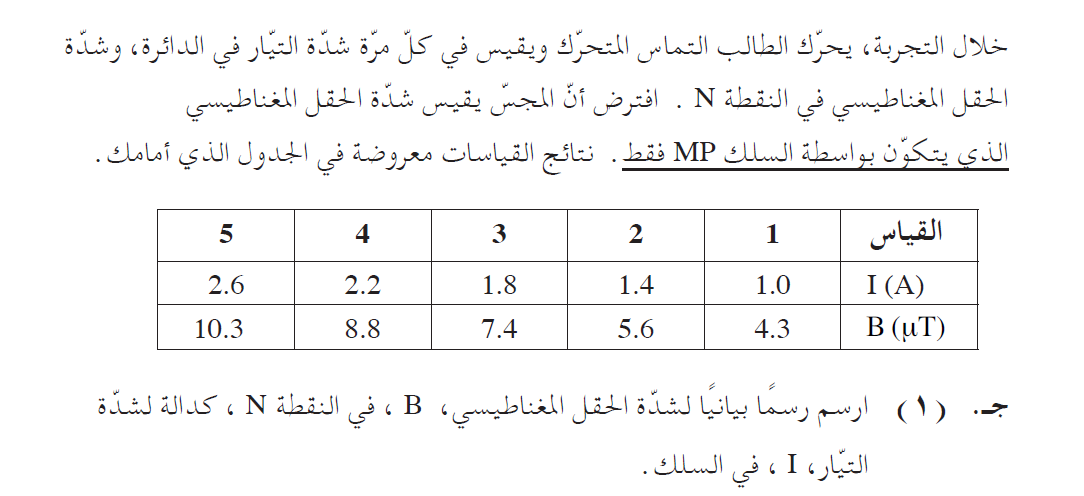
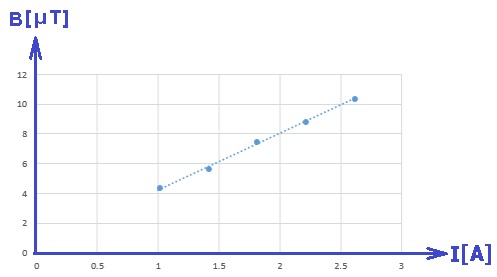
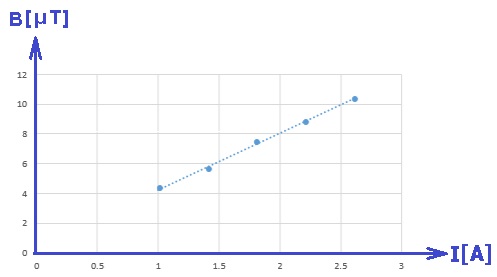
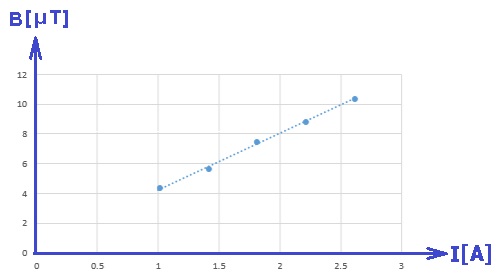
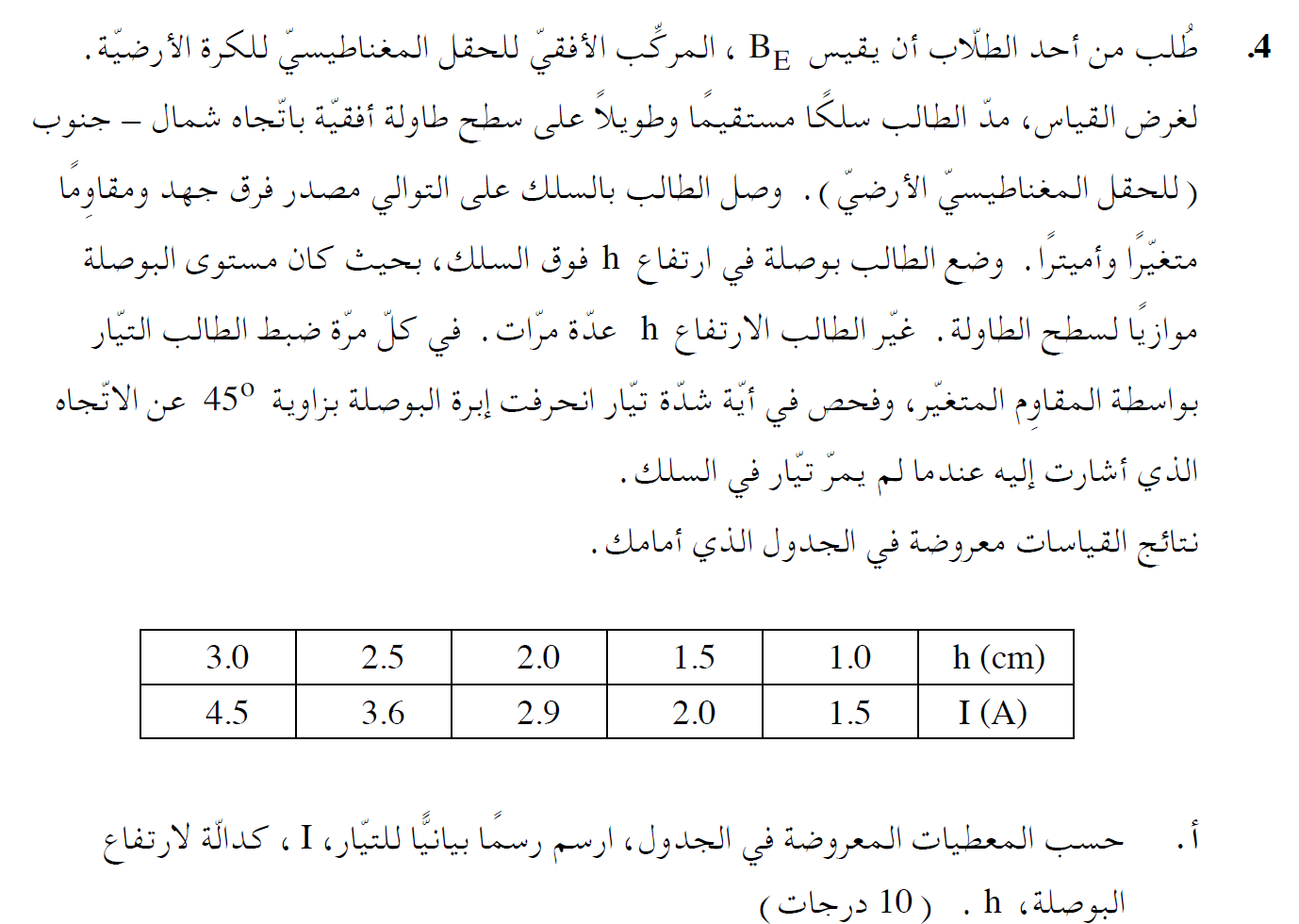
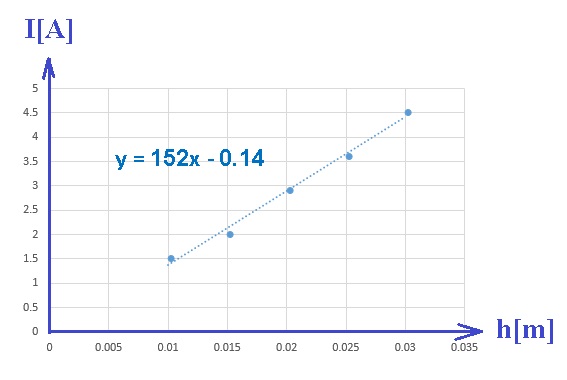
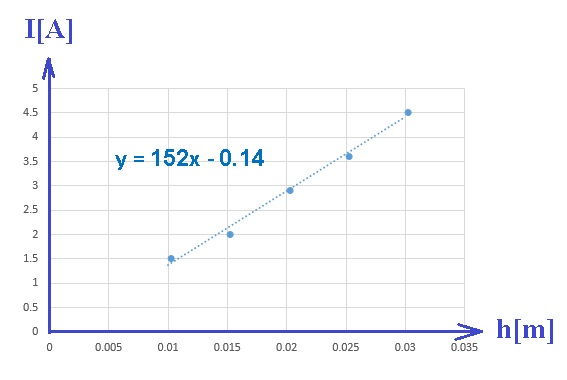
رسم رسمًا بيانيًا وفقا للمعطيات الموجودة في الجدول.
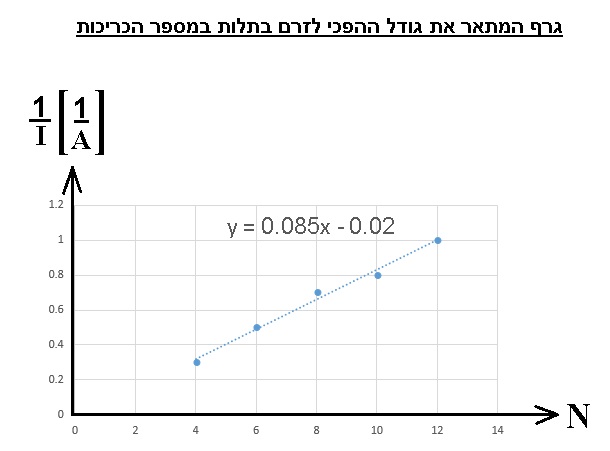
بناءً على البيانات الموجودة في الجدول، نقوم برسم رسمًا بيانيًا يصف القيمة العكسية للتيار بدبالة عدد اللفّات:
1. من المهم الإشارة إلى وحدات المقادير الموصوفة على محاور الرسم البياني، حيث تظهر الوحدات في الجدول.
2. عدد اللفّات ليس له وحدات. يجب كتابة اسم المقدار الفيزيائي فقط. י
3. من تعبير الدالة يتضح أن الرسم البياني خطي، والبيانات الموجودة في الجدول مبنية على نتائج تجريبية
وبالتالي فإن توزيع النقاط ليس بالضبط على طول خط مستقيم. يجب إضافة خط الاتجاه واستخلاص النتائج منه فقط.
2.למספר הכריכות אין יחידות. יש לכתוב רק את שמו של הגודל הפיזיקלי.
3. מביטוי הפונקציה ברור שהגרף הוא ליניארי, נתוני הטבלה מבוססים על תוצאות ניסוי
לכן פיזור הנקודות הוא לא בדיוק לאורך קו ישר. יש להוסיף את הישר המסתבר ביותר ורק ממנו להפיק את המסקנות.
______________________________________________________________________________________
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨»B«/mi»«mrow»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8869;«/mo»«/mrow»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»69«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨»T«/mi»«/math»
من تعبير الدالة في الرسم البياني، يمكن ايجاد تعبير الميل.
نكتب تعبيرًا للدالة الموصوفة في الرسم البياني، من تعبير الحقل المغناطيسي الموجود في مركز الملف الدائري الدقيق:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8869;«/mo»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»B«/mi»«mrow»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8869;«/mo»«/mrow»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/mstyle»«/math»
تعبير ميل الرسم البياني: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#956;«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»0«/mn»«/msub»«mrow»«mn mathvariant=¨bold¨ mathsize=¨20px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»r«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»B«/mi»«mrow»«mi mathvariant=¨bold¨ mathsize=¨20px¨»E«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#8869;«/mo»«/mrow»«/msub»«/mrow»«/mfrac»«/math» .
من دالة الخط المستقيم «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»085«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»02«/mn»«/math» قيمة ميل الخط المستقيم «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»085«/mn»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»A«/mi»«/mfrac»«/math».
سنقوم بمقارنة تعبير الميل بقيمته:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨16px¨»«mrow»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»B«/mi»«mrow»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8869;«/mo»«/mrow»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»085«/mn»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»A«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8869;«/mo»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»085«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»085«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»256«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»034«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»69«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/mrow»«/mstyle»«/math»
مقدار المركَّب العموي للحقل المغناطيسي للأرض يساوي 36.9 ميكرو تسلا.
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8869;«/mo»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»B«/mi»«mrow»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8869;«/mo»«/mrow»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/mstyle»«/math»
ביטוי שיפוע הגרף הוא: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#956;«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»0«/mn»«/msub»«mrow»«mn mathvariant=¨bold¨ mathsize=¨20px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»r«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»B«/mi»«mrow»«mi mathvariant=¨bold¨ mathsize=¨20px¨»E«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#8869;«/mo»«/mrow»«/msub»«/mrow»«/mfrac»«/math» .
מפונקציית הישר «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»085«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»02«/mn»«/math» ערך שיפוע הישר הוא «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»085«/mn»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»A«/mi»«/mfrac»«/math».
נשווה בין ביטוי השיפוע לערכו:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨16px¨»«mrow»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»B«/mi»«mrow»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8869;«/mo»«/mrow»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»085«/mn»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»A«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8869;«/mo»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»085«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»085«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»256«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»034«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»69«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/mrow»«/mstyle»«/math»
גודל הרכיב האנכי של השדה המגנטי של כדור הארץ שווה ל 36.9 מיקרו טסלה.
1. يتم حساب الميل باستخدام برنامج إكسل، وفي دفتر الامتحان يجب حساب الميل بالإعتماد على نقطتين على خط الاتجاه.
2. في كل سؤال يحتوي على رسم بياني، عليك استخدام المبادئ الفيزيائية أو الرياضية لإيجاد الدالة في الرسم البياني.
3. عند كتابة قيمة ميل الدالة يجب كتابة وحدات الميل.
4. في أغلب الأسئلة التي تتناول الحقل المغناطيسي للأرض يجب إيجاد مركَّب الحقال المغناطيسي الأفقي وليس مركَّب الحقال المغناطيسي العمودي.
من حيث المبدأ، في كلتا الحالتين هناك علاقة هندسية بين الحقل المغناطيسي للكرة الأرض والحقل المغناطيسي الناتج عن سلك موصل يحمل تيارًا.
وفي حالة إيجاد مركَّب الحقل المغناطيسي الأفقي، يتم استخدام دالة tan الزاوية. في هذا القسم لإيجاد مركَّب الحقل المغناطيسي
العمودي استخدمنا دالة الجيب sin.
العمودي استخدمنا دالة الجيب sin.
بشكل عام، في كل حالة، يجب رسم مخطط لمتجهات الحقول المغناطيسية، ويجب إيجاد العلاقة الهندسية بين متجهات الحقل.
5. لكي تعرف كيفية تقييم الإجابة، من المهم أن تعرف أن شدة الحقل المغناطيسي على سطح الأرض تبلغ عدة عشرات من الميكرو تيسلا. عادة ما بين 30 و60 ميكرو تسلا. والنتيجة التي حصلنا عليها معقولة.
2. בכל שאלה שיש בה גרף צריך להשתמש בעקרונות הפיזיקליים או המתמטיים כדי למצוא את הפונקציה בגרף.
3. בכתיבת ערך שיפוע הפונקציה יש לכתוב את יחידות השיפוע.
4. ברוב השאלות יש העוסקות בשדה המגנטי של כדור הארץ , יש למצוא את רכיב השדה המגנטי האופקי
ולא את רכיב השדה המגנטי האנכי.
עקרונית בשני המקרים יש קשר גיאומטרי בין השדה המגנטי של כדור הארץ לשדה המגנטי הנוצר ממוליך נושא זרם.
במקרה של מציאת רכיב השדה המגנטי האופקי משתמשים בפונקציית הטנגנס . בסעיף זה למציאת רכיב השדה המגנטי
האנכי השתמשנו בפונקציית הסינוס.
באופן כללי יש לערוך לכל מקרה תרשים של ווקטורי השדה המגנטי , ולמצוא את הקשר הגיאומטרי שבין וקטורי השדה.
5. כדי לדעת להעריך את התשובה , חשוב לדעת שעוצמת השדה המגנטי על פני כדור הארץ הוא כמה עשרות מיקרו טסלה.
לרוב בין 30 ל 60 מיקרו טסלה. התוצאה שקבלנו היא סבירה.
______________________________________________________________________________________
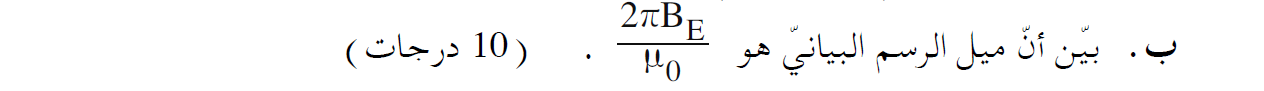
2. 2014,5- مصفاة السرعة ومطياف الكتل
______________________________________________________________________________________
...
في اتجاه موازٍ للمحور X بحيث تكون القوة المغناطيسية صفراً.
التعبير عن القوة المغناطيسية المؤثرة على شحنة تتحرك في حقل مغناطيسي«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»)«/mo»«/math» .
من التعبير عن القوة المغناطيسية المؤثرة على شحنة تتحرك في حقل مغناطيسي «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math» عندما تتحرك الشحنة في اتجاه الحقل المغناطيسي
الزاوية بين متجه السرعة ومتجه الحقل المغناطيسي تساوي صفر درجة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/math» , القوة المغناطيسية تساوي صفر نيوتن.
لذلك، إذا كان اتجاه الحقل المغناطيسي في اتجاه المحور X لكي تتحرك الشحنة في خط مستقيم، يجب أن تتحرك الشحنة بشكل موازٍ للمحور X.
הזווית שבין וקטור המהירות לוקטור השדה המגנטי שווה לאפס מעלות «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/math» , הכוח המגנטי שווה לאפס ניוטון.
לכן, אם כיוון השדה המגנטי הוא בכיוון ציר X כדי שהמטען ינוע בקו ישר המטען צריך לנוע במקביל לציר X.
1. حتى لو تحركت الشحنة في الاتجاه المعاكس للمحور X ( «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»180«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#176;«/mo»«/math») لن تكون هناك قوة مغناطيسية وستستمر الشحنة في التحرك بسرعة ثابتة.
2. تعمل القوة المغناطيسية دائمًا بشكل عمودي على الحركة، بحيث تستمر الشحنة في الحركة في خط مستقيم، ويجب أن يكون مقدار القوة المغناطيسية صفر نيوتن.
3.التعبير عن القوة المغناطيسية يكون مُعطى في قوانين البجروت.
4. مكتوب في الجملة الأولى أن هناك حقلًا كهربائيًا وحقلًا مغناطيسيًا أيضًا. لكن الحقل الكهربائي يعمل فقط في المرحلة الثانية وليس في المرحلة الأولى
2. הכוח המגנטי פועל תמיד בניצב לתנועה, כדי שהמטען ימשיך לנוע בקו ישר גודלו של הכוח המגנטי חייב להיות אפס ניוטון.
3. ביטוי הכוח המגנטי נתון בדפי בנוסחאות.
______________________________________________________________________________________
______________________________________________________________________________________
...
تتحرك الجسيمات في خط منحنٍ، تؤثر عليها قوة مغناطيسية.
تعمل القوة المغناطيسية دائمًا بشكل عمودي على الحركة، وطالما أن القوة المغناطيسية تعمل فإن الجسيم لن يتحرك في خط مستقيم.
منذ اللحظة التي تتحرر فيها الجسيمات من حالة السكون، ستؤثر عليها قوة كهربائية، وستتحرك بتسارع ثابت في اتجاه الحقل، موازيًا للمحور Y.
يكون اتجاه الحقل المغناطيسي في اتجاه المحور X، فمنذ اللحظة التي تبدأ فيها الجسيمات بالتحرك، تعمل عليها أيضًا قوة مغناطيسية باتجاه عمودي على الحركة.
سوف تتسبب القوة المغناطيسية في تحرك الجسيمات في مسار منحنٍ.
כיוון השדה המגנטי הוא בכיוון ציר X, החל מרגע תחילת תנועת החלקיקים פועל עליהם גם כוח מגנטי בניצב לתנועה.
הכוח המגנטי יגרום לחלקיקים לנוע במסלול עקום.
1. في لحظة تحرير الجسيمات، لا تعمل أي قوة مغناطيسية، بل تعمل القوة الكهربائية فقط.
لكن السؤال يتناول حركة الشحنات من لحظة تحريرها وليس فقط لحظة تحريرها.
2. يجب عليك أن تفهم ما يحدث لجسيم واحد، وبالتالي فهم ما يحدث لجميع الجسيمات.
ومن حيث نوع الحركة، فإن سلوك جميع الجزيئات هو نفسه.
3. ليس من الضروري أن يكون الخط المنحني في مستوى، ففي هذه الحالة تكون الحركة في المستوى Z-Y.
4. يمكن أن نفهم من هذا البند والند السابق أن مُعطيات الحركة الأولية هي التي تحدّد شكل مسار الجسيم.
وهذا ليس مستغربا، فحتى لو قذف جسم في اتجاه الجاذبية فإنه يتحرك في خط مستقيم. وإذا رميت في اتجاه أفقي فإنها تتحرك في مسار منحنٍ.
אך, השאלה עוסקת בתנועת המטענים מרגע שחרורם ולא רק ברגע שחרורם.
2. יש להבין מה קורה עם חלקיק אחד , ובהתאם להבין מה קורה עם כל החלקיקים.
מבחינת סוג התנועה התנהגות כל החלקיקים היא זהה .
3. קו עקום לא חייב להיות במישור , במקרה זה התנועה היא במישור Z-Y.
______________________________________________________________________________________
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»B«/mi»«/mfrac»«/math»
مُحدّد السرعات.
يعمل الحقل المغناطيسي في اتجاه المحور X، ويعمل الحقل الكهربائي في اتجاه المحور Y، وتتحرك الجسيمات في اتجاه المحور Z.
في هذه الحالة تعمل القوة الكهربائية FE في الاتجاه الموجب للمحور Y، وحسب قاعدة اليد اليسرى وفقًا لاتجاه الحقل المغناطيسي واتجاه الحركة
ستعمل القوة المغناطيسية في الاتجاه السالب للمحور Z.
في الشكل التالي، يتم وصف متجهات الحقول والقوى ومتجهات السرعة:
الشرط حتى تتحرك الجسيمات في خط مستقيم هو أن يكون مقدار القوة المغناطيسية مساوياً لمقدار القوة الكهربائية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«/mrow»«/mstyle»«/math»
نكتب بشكل صريح كل من القوتين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
الزاوية بين اتجاه الحركة واتجاه الحقل 90 درجة، نُعبّر عن السرعة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»q«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»90«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»q«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»B«/mi»«/mfrac»«/menclose»«/mstyle»«/math»
العلاقة بين الحقلين وسرعة الشحنة حتى تتحرك الشحنة في خط مستقيم هي: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathsize=¨20px¨»E«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»B«/mi»«/mfrac»«/math»
במצב זה, הכוח החשמלי FE פועל בכיוון החיובי של ציר Y, ולפי כלל יד שמאל בהתאם לכיוון השדה המגנטי ולכיוון התנועה
יפעל כוח מגנטי בכיוון השלילי של ציר ה Z.
באיור הבא מתוארים וקטורי השדות, הכוחות והמהירות:
התנאי לכך שהחלקיקים ינועו בקו ישר הוא שגודל הכוח המגנטי צריך להיות שווה לגודל הכוח החשמלי:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«/mrow»«/mstyle»«/math»
נכתוב בצורה מפורשת את כל אחד משני הכוחות:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
הזווית בין כיוון התנועה לכיוון השדה היא 90 מעלות, נבטא את המהירות :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»q«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»90«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»q«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»B«/mi»«/mfrac»«/menclose»«/mstyle»«/math»
הקשר בין השדות למהירות כדי שהמטען ינוע בקו ישר הוא: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathsize=¨20px¨»E«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»B«/mi»«/mfrac»«/math»
1. عندما تتحرك شحنة بشكل عمودي لحقل مغناطيسي وحقل كهربائي متعامدين مع بعضهما البعض، تعمل هذه المنظومة كمحدّد للسرعة.
2. من المهم معرفة محدّد السرعة وتعبير السرعة بدلالة كل من الحقلين.
2. חשוב להכיר את בורר המהירויות ואת ביטוי המהירות בתלות בשדות.
______________________________________________________________________________________
______________________________________________________________________________________
...
سوف تتحرك الجزيئات في حركة دائرية.
معرفة تأثير القوة المغناطيسية.
تدخل الشحنات بشكل عمودي لخطوط الحقل المغناطيسي، وتؤثر القوة المغناطيسية على الشحنات باتجاه متعامدة مع حركتها، وبالتالي تتحرك الشحنات في حركة دائرية.
1. تعمل القوة المغناطيسية دائمًا بشكل عمودي على الحركة وبالتالي فهي تعمل كقوة جاذبة نحو المركز وتسبب حركة دائرية.
2. لو دخلت الشحنة بزاوية غير 90 درجة بالنسبة للحقل لتحركت بحركة حلزونية (حركة حلزونية).
3. مصدر الجسيمات الموضح في التخطيط (ب) هو محدّد السرعة الذي تطرقنا له في البند السابق.
4. ليست هناك حاجة للتفسير إنما فقط لوصف حركة الجسيمات.
5. يجب افتراض أنّ الجسيمات لا تصطدما أثناء حركتها.
2. אם המטען היה נכנס בזווית שונה מ 90 מעלות ביחס לשדה הוא היה נע בתנועה בורגית(תנועת ספירלה).
3. מקור החלקיקים המופיע בתרשים ב' הוא בורר המהירויות בו עוסק הסעיף הקודם.
______________________________________________________________________________________
______________________________________________________________________________________
...
يتعلق نصف قطر المسار على كتلة الجسيمات «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»E«/mi»«/mrow»«mrow»«msup»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«/math» , ولذلك يمكن استخدام المنظومة لفصل النظائر.
مطياف الكتلة.
النظير هو ذرة عنصر معين يحتوي على عدد من النيوترونات يختلف عن عدد نيوترونات ذلك العنصر في الطبيعة.
نظائر نفس العنصر لها نفس الشحنة (نفس عدد البروتوفات) وكتلة مختلفة.
القوة الوحيدة المؤثرة على الجسيمات هي القوة المغناطيسية، التي تعمل كقوة جاذبة نحو المركز:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
تتحرك الشحنة بشكل عمودي على الحقل، والزاوية α تساوي 90 درجة. نُعبّر عن نصف قطر المسار:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»V«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»90«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«menclose notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
الحقل المغناطيسي الذي تدخل إليه الجسيمات هو نفس الحقل المغناطيسي في محدّد السرعة (مصدر الجسيمات).
إن السرعة التي تدخل بها الجسيمات إلى داخل الحقل المغناطيسي تساوي السرعة التي تتحرك بها في خط مستقيم داخل محدّد السرعة.
نعبّر عن السرعة بدلالة النسبة بين الحقلين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mstyle displaystyle=¨true¨»«mfrac»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»B«/mi»«/mfrac»«/mstyle»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»E«/mi»«/mrow»«mrow»«msup»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«/menclose»«mspace linebreak=¨newline¨/»«/math»
من هذا التعبير يمكن ملاحظة أن نصف القطر يتناسب طرديًا على كتلة الجسيمات، لذا النظائر ذات الكتلة الأكبر ستتحرك بنصف قطر أكبر،
والنظائر ذات الكتلة الأصغر سوف تتحرك في نصف قطر أصغر.
هذه هي الطريقة التي تعمل بها المنظومة الموضحة في الشكل (ب) على فصل النظائر، ويسمى هذا الجهاز بمطياف الكتلة.
לאיזוטופים מאותו יסוד יש מטען זהה ומסה שונה.
נכתוב
1. يجب معرفة ما هو النظير للإجابة على هذا البند. وقد تمت دراسة تفسير النظير في الفصل الخاص بمبنى المادة في بداية دراسة الكهرباء.
(الوحدة 35)، في الماضي تمت دراسة موضوع الأشععة والمادة بالتفصيل، وتم دراسة مفهوم النظائر بطريقة أكثر تعمقًا.
2. التحدي في هذا السؤال هو فهم أن مصدر الجسيمات هو محدّد السرعة. و"فصل نظائر أي عنصر" يعني مطياف الكتلة.
في الواقع، السؤال يتناول الجسيمات التي تتحرك داخل محدّد السرعة وتمر عبر مطياف الكتلة.
ويتكرر هذان التطبيقان في كثير من الأسئلة التي تتناول الحقل المغناطيسي.
3. للنجاح في حل أسئلة البجروت في الحقل المغناطيسي، من المهم معرفة كيفية تطوير تعبير لنصف قطر المسار وزمن الدورة
(لا يظهر كلا التعبيرين في قوانين البجروت). ولمعرفة التطبيقات: محدّد السرعة، ومطياف الكتلة، والسيكلوترون (الوحدة 46).
(קיוב 35), בעבר נלמדו נושאי קרינה וחומר בהרחבה , תלמידים הכירו את מושג האיזוטופ בצורה יותר מעמיקה.
2. האתגר בשאלה זו הוא להבין שמקור החלקיקים הוא בורר מהירויות. ו"בהפרדת איזוטופים של יסוד כל שהוא"
מתכוונים לספקטרוגרף מסות.
למעשה, השאלה עוסקת בחלקיקים הנעים בתוך בורר מהירויות ועוברים לספקטרוגרף מסות.
שני יישומים אלו חוזרים על עצמם בשאלות רבות העוסקות בשדה המגנטי.
______________________________________________________________________________________
3. 2013,4 - إيجاد المركب الأفقي للحقل المغناطيسي الأرضي بواسطة لسلك مستقيم
______________________________________________________________________________________
...
وصف المعطيات المعروضة في الجدول في رسم بياني.
سنرسم رسمًا بيانيًا يصف التيار كدالة لارتفاع البوصلة h فوق السلك. الارتفاعات معطاة بوحدات سم، وسنصفها في الرسم البياني بوحدات الأمتار.
من الممكن وصف قيم الارتفاع بوحدات سم.
ولكي تكون وحدات الميل قياسية، يجب وصف قيم الارتفاع بوحدات الأمتار.
כדי שהיחידות של השיפוע יהיו תקינות יש לתאר את ערכי הגובה ביחידות של מטר.
______________________________________________________________________________________
______________________________________________________________________________________
...
من دالة الرسم البياني: «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»=«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨ mathsize=¨20px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»B«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»E«/mi»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#956;«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»0«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»h«/mi»«/math» ميل الرسم البياني هو : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac»«mrow»«mn mathvariant=¨bold¨ mathsize=¨20px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»B«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»E«/mi»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#956;«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»0«/mn»«/msub»«/mfrac»«/math»
تطوير تعبير للدالة الموصوفة في الرسم البياني، باستخدام تعبير الحقل المغناطيسي بالقرب من موصل يمر به تيارًا مباشرًا.
نرسم مخططًا عامًا يحتوي على الدائرة الكهربائية ومتجهي الحقل المغناطيسي والبوصلة.
يعمل الحقل المغناطيسي BE باتجاه الشمال، ويعمل الحقل الناتج عن التيار BI بشكل عمودي باتجاه الشرق (خارج الصفحة).
تشير إبرة البوصلة إلى اتجاه الحقل المحصّل BT.
نقوم بتغيير شدة التيار في الدائرة بحيث تكون زاوية ميل البوصلة في أي ارتفاع 45 درجة، كما هو موضح في الشكل التالي:
يمكنك استخدام دالة الظل (tan) وإظهار أنه عندما تكون زاوية ميل إبرة البوصلة 45 درجة فإن شدة BE تساوي شدة BI:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»45«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«msub»«mi mathvariant=¨bold¨»B«/mi»«mi mathvariant=¨bold¨»I«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»B«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mfrac»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»B«/mi»«mi mathvariant=¨bold¨»I«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»B«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«/msub»«/mstyle»«/math»
نعبّر عن شدة الحقل المغناطيسي BI، باستخدام التعبير عن الحقل المغناطيسي على بعد r من سلك موصل مستقيم يحمل تيارًا.
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«/mrow»«/mstyle»«/math»
البعد العمودي بين السلك الموصل والبوصلة r يساوي h وشدة الحقل المغناطيسي BI تساوي شدة الحقل المغناطيسي BE
نكتب تعبيرًا لشدة التيار كدالة للارتفاع h:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»h«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»B«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
من تعبير دالة الرسم البياني يمكن ملاحظة أنه في الرسم البياني للتيار كدالة للبعد h يُمثل ميل الرسم البياني:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»B«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
השדה המגנטי BE פועל לכיוון צפון, השדה הנוצר מהזרם BI פועל לכיוון מזרח (החוצה מהדף) .
מחט המצפן מצביעה על כיוון השדה השקול BT.
משנים את עוצמת הזרם במעגל כך שבכל גובה h בו נמצא המצפן עוצמת BI שווה לעוצמת BE וזווית נטיית המצפן היא 45 מעלות.
נבטא את עוצמת השדה המגנטי BI , בעזרת ביטוי השדה המגנטי במרחק r ממוליך ישר נושא זרם.
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«/mrow»«/mstyle»«/math»
המרחק האנכי בין המוליך למצפן r שווה ל h ועוצמת השדה המגנטי BI שווה לעוצמת השדה המגנטי BE
נכתוב ביטוי לזרם כפונקציה של הגובה h:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»h«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»B«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
מביטוי הפונקציה בגרף ניתן לראות שבגרף של הזרם בתלות ב h שיפוע הגרף הוא: «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»B«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
1. هناك تفاصيل كثيرة في هذا السؤال، ومن المهم رسم مخطط عام لفهم كل تفصيل.
2. من المهم إظهار أن شدة الحقل BI تساوي شدة الحقل BE.
2. חשוב להראות שעוצמת השדה BI שווה בגודלו לעוצמת השדה BE.
2. באופן כללי כאשר נתון גרף כלשהוא חשוב למצוא את ביטוי לפונקציה בגרף, מהביטוי ניתן ללמוד על משמעות שיפוע הגרף.
______________________________________________________________________________________
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub»«mi mathvariant=¨bold¨»B«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»30«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«mi mathvariant=¨bold¨»§#956;T«/mi»«/mrow»«/mstyle»«/math»
مقارنة بين قيمة الميل والتعبير عن ميل الدالة.
من معادلة الخط المستقيم: Y=152X- 0.14 قيمة ميل الخط المستقيم «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»152«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»A«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/math» , نقارن تعبير الميل ومقداره.
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»B«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»152«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»152«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»152«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
לכן, גודל הרכיב האופקי של השדה המגנטי הוא 30.4 מיקרו טסלה.
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»B«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»152«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»152«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»152«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
לכן, גודל הרכיב האופקי של השדה המגנטי הוא 30.4 מיקרו טסלה.
1. غالبًا ما يستخدم BE كوصف لقيمة الحقل المغناطيسي نفسه، وفي هذا السؤال يكون معنى BE هو المركّب الأفقي لشدة الحقل المغناطيسي للكرة الأرضية.
2. شدة المركّب الأفقي للحقل المغناطيسي الأرضي حوالي 30 ميكرو تسلا.
3. BE لا يمكن تغييره لأنه ثابت، في كل تجربة لايجاد المركّب BE نقوم بتغيير كمية فيزيائية معينة ونتحقق من مقدار فيزيائي آخر تم نحسب المركّب BE تجريبيًا من ميل الرسم البياني.
2. עוצמת הרכיב האופקי של כדור הארץ הוא בסביבות 30 מיקרו טסלה.
3. קיים ביטוי לעוצמת השדה המגנטי בסביבת מוליך נושא זרם.
קביעת הזרם כך שבכל גובה זווית נטיית מחט המצפן סוטה ב 45 מעלות מאפשרת לכתוב ביטוי לעוצמה של השדה המגנטי
______________________________________________________________________________________
______________________________________________________________________________________
...
عندما يكتب الطالب 2.0A، يحدد أن الرقم الموجود على يمين العلامة العشرية يساوي صفرًا.
القليل من المنطق.
عندما يكتب الطالب 2.0A، فإنه يشير إلى قيمة الرقم الموجود على يمين المنزلة العشرية ويذكر أن هذه القيمة تساوي الصفر.
تحدّد قيمة هذا الرقم الفرق بين القياس الثالث والرابع، وبالتالي فإن قيمة الرقم مهمة.
ערך ספרה זו קובע את ההבדל שבין המדידה השלישית לרביעית, לכן ערך הספרה הוא חשוב .
ערך ספרה זו חשוב. ניתן לראות שההבדל בין המדידה השלישית לרביעית הוא רק בספרה שמימין לנקודה העשרונית.
1. هناك أسئلة عامة جدًا، وهناك أسئلة مختلفة، ولم تكن هناك أسئلة متشابهة في الامتحانات السابقة.
عليك أن تتعامل مع مثل هذه الأسئلة حتى لو لم تكن واثقًا تمامًا من فهم السؤال.
2. من المهم أن نتذكر أن السؤال تم طرحه في اامتحان الفيزياء، ويجب على المتقدم للامتحان إظهار الكفاءة في المفاهيم والمفاهيم الفيزيائية.
إجابات مثل: كتب الطالب 2.0A لأنه هكذا اعتادوا على الكتابة في مدرستهم، أو أنها كتابة أكثر حداثة أو أجمل.
سيتم اعتبار مثل هذه الإجابات بمثابة إجابات غير صحيحة.
______________________________________________________________________________________
______________________________________________________________________________________
...
رأس إبرة البوصلة هو قطب شمالي مغناطيسي، لذا فهو يتجه القطب الجنوبي المغناطيسي للأرض.
معرفة الأقطاب المغناطيسية للأرض وإبرة البوصلة.
رأس إبرة البوصلة هو قطب شمالي مغناطيسي، ولذلك فهو يتجه نحو القطب الجنوبي المغناطيسي للأرض.
ويجب معرفة موضوع الأقطاب المغناطيسية للإبرة والأقطاب المغناطيسية للكرة الأرضية.
كل جسم مغناطيسي له قطبين مغناطيسيين: القطب الشمالي المغناطيسي والقطب المغناطيسي الجنوبي. الأرض جسم مغناطيسي.
وإبرة البوصلة هي أيضًا جسم مغناطيسي.
وإبرة البوصلة هي أيضًا جسم مغناطيسي.
في المغناطيسية تتجاذب الأقطاب المختلفة ونفس الأقطاب تتنافر.
في الشكل التالي، تم وصف الكرة الأرضية على شكل دائرة وفي داخلها إبرة البوصلة. تم تحديد الأقطاب المغناطيسية الجنوبية باللون الأخضر.
تم تحديد الأقطاب المغناطيسية الشمالية باللون الأزرق.
تم تحديد الأقطاب المغناطيسية الشمالية باللون الأزرق.
לכל גוף מגנטי יש שני קטבים מגנטיים: קוטב צפוני מגנטי וקוטב דרומי מגנטי. כדור הארץ הוא גוף מגנטי .
וגם מחט המצפן היא גוף מגנטי.
במגנטיות קטבים שונים נמשכים וקטבים זהים נדחים.
באיור הבא מתואר כדור הארץ כעיגול ובתוכו מחט המצפן. הקטבים המגנטיים הצפוניים מסומנים בירוק.
הקטבים המגנטים הדרומיים מסומנים בכחול.
______________________________________________________________________________________
هـ. 
______________________________________________________________________________________
...
يتّجه القطب الشمالي لإبرة البوصلة إلى القطب الجغرافي الشمالي .
معرفة موقع الأقطاب المغناطيسية بالنسبة للأقطاب الجغرافية.
يتّجه القطب الشمالي لإبرة البوصلة إلى القطب الشمالي الجغرافي. لأن القطب المغناطيسي الجنوبي للكرة الأرضية يقع بالقرب من القطب الجغرافي الشمالي.
1. الأرض لها أقطاب مغناطيسية وأقطاب جغرافية، وإبرة البوصلة لها أقطاب مغناطيسية فقط. في الشكل التالي يتم وصف القطبين
المغناطيسيين والجغرافيين للكرة الأرضية:
2. مكتوب في هذا البند "تقريبًا" لأن الأقطاب المغناطيسية ليست بالضبط في القطبين الجغرافيين.
3. من المهم أن نتذكر شيئين مهمين حول القطبين المغناطيسيين للأرض:
א. يتواجد القطب المغناطيسي الشمالي بالقرب من القطب الجغرافي الجنوبي،
وبالقرب من القطب الجغرافي الجنوبي يتواجد القطب المغناطيسي الشمالي.
ب. رأس إبرة البوصلة هو دائمًا القطب المغناطيسي الشمالي . بحيث يشير رأس إبرة البوصلة إلى الجغرافي الشمالي.
4. في كلا البندين 1 و 2، مكتوب -بدون تفسير-، ومع ذلك فمن المفضل التفسير.
2. בסעיף זה כתוב "בקירוב" מכיוון שהקטבים המגנטיים לא נמצאים בדיוק בקטבים הגיאוגרפיים.
3. חשוב לזכור שני דברים חשובים בנושא הקטבים המגנטיים של כדור הארץ:
1. בסמוך לקוטב הגיאוגרפי הצפוני נמצא קוטב מגנטי דרומי ,
ובסמוך לקוטב הגיאוגרפי הדרומי קיים קוטב מגנטי צפוני.
2. ראש מחט המצפן היא תמיד קוטב צפוני מגנטי.
4. על שני הסעיפים ה.1 ו- ה.2 כתוב -בלי לנמק- , בכל זאת כדאי לנמק .
______________________________________________________________________________________
4. 2011,4- تتسارع أيونات داخل حقل كهربائي وتدخل إلى المطياف
______________________________________________________________________________________
...
اتجاه الحقل المغناطيسي يخرج من الصفحة حسب قاعدة اليد اليسرى.
قاعدة اليد اليسرى.
أيون الهيدروجين وأيون الهيليوم مشحونان بشحنة موجبة، فعندما تكون الأيونات في النقطة A تؤثر عليهما قوة إلى اليمين حسب اتجاه حركتهما وحسب قاعدة اليد اليسرى ينتج أنّ اتجاه الحقل المغناطيسي نحو الخارج.
1. وفقًا لاتجاه حركة الشحنة يمكن معرفة اتجاه القوة المغناطيسية المؤثرة عليها.
2. لتحديد اتجاه الحقل المغناطيسي، نستخدم قاعدة اليد اليسرى في نقطة واحدة في مسار حركة الشحنة.
3. عادة يكون مُعطى اتجاه الحقل واتجاه الحركة ويُطلب تحديد اتجاه القوة المغناطيسية وفقا لذلك ويتم تحديد الاتجاه باستخدام قاعدة اليد اليسرى.
في هذه الحالة يجب معرفة اتجاه الحقل المغناطيسي،من المفروض أن يكون اتجاه الحقل ربما يكون داخل الصفحة أو خارجها،
ونتحقق باستخدام قاعدة اليد اليسرى لكل خيار من الخيارين.
2. כדי למצוא את כיוון השדה המגנטי יש להשתמש בכלל יד שמאל בנקודה אחת במסלול תנועת המטען.
3. בדרך כלל, נתון כיוון השדה וכיוון התנועה ויש למצוא את כיוון הכוח המגנטי בהתאם בעזרת כלל יד שמאל.
במקרה זה יש למצוא את כיוון השדה המגנטי , מומלץ להניח שכיוון השדה הוא ככל הנראה לתוך הדף או אל מחוץ הדף,
ולבדוק עם כלל יד שמאל כל אחת משתי האפשרויות.
______________________________________________________________________________________
______________________________________________________________________________________
...
لا تتغير السرعة لأن القوة المغناطيسية تعمل بشكل عمودي على الحركة.
قانون الشغل والطاقة أو الديناميكا.
تعمل القوة المغناطيسية باتجاه عمودي على الحركة، من تعريف الشغل: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»c«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»o«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math» , الشغل الذي تبذله القوة المغناطيسية يساوي صفرًا.
من قانون الشغل والطاقة: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathcolor=¨#0000FF¨ mathvariant=¨bold¨»K«/mi»«/msub»«/math» , نظرًا لعدم بذل أي شغل، لا يحدث أي تغيير في الطاقة الحركية.
وبالتالي فإن مقدار السرعة لا يتغير.
ממשפט העבודה אנרגיה: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathcolor=¨#0000FF¨ mathvariant=¨bold¨»K«/mi»«/msub»«/math» , מכיוון שלא מבוצעת עבודה אין שינוי באנרגיה הקינטית.
מכאן שהמהירות לא משתנה בגודלה.
1. لا يتغير مقدار السرعة ولكن اتجاهها يتغير.
2. يمكن أيضًا الإجابة على السؤال من مبادئ الديناميكا. تعمل القوة المغناطيسية دائمًا بشكل عمودي على الحركة، وليس لها أي مركّب في اتجاه الحركة
أو في الاتجاه المعاكس للحركة فلا يؤثر على مقدار السرعة. إنه يؤثر فقط على اتجاه الحركة.
3. تعمل القوة المغناطيسية دائمًا في اتجاه عمودي على الحركة، وبالتالي فهي تتحرك في حركة دائرية منتظمة.
4. القوة الجاذبة المركزية لا تبذل شغل لأنها متعامدة للحركة، وبالتالي لا يتم بذل طاقة، وهكذا تتحرك الأجسام السماوية دون استثمار طاقة.
وبالمثل، يتحرك الإلكترون أيضًا في حركة كوكبية حول البروتون.
2. אפשר לענות על השאלה גם מעקרונות הדינמיקה. הכוח המגנטי פועל תמיד בניצב לתנועה אין לו רכיב בכיוון התנועה
או בכיוון הנגדי לתנועה, לכן הוא לא משפיע על גודל המהירות. הוא משפיע רק על כיוון התנועה.
3. הכוח המגנטי תמיד פועל בכיוון ניצב לתנועה, לכן הוא תמיד גורם לתנועה מעגלית קצובה.
______________________________________________________________________________________
______________________________________________________________________________________
...
زمن حركة أيون الهيدروجين هو: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«/math»
التعبير عن زمن الدورة لشحنة تتحرك في حركة دائرية.
زمن حركة أيون الهيدروجين في الحقل المغناطيسي يساوي نصف زمن الدورة. نًطوِّر تعبيرًا لزمن الدورة:
نرسم مخططًا للقوى التي تعمل على أيون الهيدروجين عند مروره بالنقطة A:
نكتب معادلة القوى:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»
تتحرك الكرة في مستوى عمودي على الحقل المغناطيسي ولذلك: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/math», نعبر عن زمن الدورة من معادلة الحركة الجاذبة المركزية.
ونعبر عن السرعة الخطية كدالة للسرعة الزاوية:
ونعبر عن السرعة الخطية كدالة للسرعة الزاوية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»90«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»§#969;«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»
يتحرك أيون الهيدروجين لمدة زمنية نصف دورة، نحسب زمن حركة أيون الهيدروجين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«/math»
وبالتالي فإن التعبير لزمن حركة أيون الهيدروجين هو: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«/math»
נערוך תרשים כוחות ליון המימן כאשר הוא חולף בנקודה A:
נכתוב את משוואת התנועה :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»
הכדור נע במישור הניצב לשדה המגנטי לכן «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/math», נבטא את זמן המחזור ממשוואת התנועה הצנטריפטאלית.
נבטא את המהירות הקווית בתלות במהירות הזוויתית:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»90«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»§#969;«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»
יון המימן נע במשך חצי זמן מחזור, נחשב את זמן תנועת יון המימן:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«/math»
לכן, ביטוי זמן תנועת יון המימן הוא:
1. يجب أن يُفهم من الرسم البياني أن زمن حركة أيون الهيدروجين هو نصف زمن الدورة.
2. حركة أيون الهيدروجين لا تتعلق على حركة أيون الهيليوم .
2. תנועת יון המימן איננה תלויה בתנועת יון ההליום.
______________________________________________________________________________________
ج. 
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»4«/mn»«/math»
التعبير عن زمن الدورة.
نعبر عن النسبة بين زمن حركة أيون الهيليوم وزمن حركة أيون الهيدروجين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»t«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»t«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle displaystyle=¨true¨»«mfrac»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«menclose notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/mfrac»«/mstyle»«mstyle displaystyle=¨true¨»«mfrac»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«menclose notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/mfrac»«/mstyle»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle displaystyle=¨true¨ mathvariant=¨bold¨»«msub»«mi»T«/mi»«mi»HE«/mi»«/msub»«/mstyle»«mstyle displaystyle=¨true¨ mathvariant=¨bold¨»«msub»«mi»T«/mi»«mi»H«/mi»«/msub»«/mstyle»«/mfrac»«/math»
النسبة بين زمني حركة الأيونين تساوي النسبة بين زمني الدورة، نجد هذه النسبة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle displaystyle=¨true¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«/mrow»«/mfrac»«/mstyle»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«/mfrac»«/math»
شحنة الهيليوم وشحنة الهيدروجين متساويتان في المقدار، وكتلة الهيليوم أكبر بأربع مرات من كتلة الهيدروجين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle displaystyle=¨true¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«/mrow»«/mfrac»«/mstyle»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle mathvariant=¨bold¨ displaystyle=¨true¨»«mfrac»«mrow»«menclose notation=¨horizontalstrike¨»«mn»2«/mn»«mo»§#183;«/mo»«mi»§#960;«/mi»«/menclose»«mo»§#183;«/mo»«mn»4«/mn»«mo»§#183;«/mo»«msub»«mi»m«/mi»«mi»H«/mi»«/msub»«/mrow»«menclose notation=¨downdiagonalstrike¨»«mi»B«/mi»«mo»§#183;«/mo»«msub»«mi»q«/mi»«mi»H«/mi»«/msub»«/menclose»«/mfrac»«/mstyle»«mfrac»«mrow»«menclose notation=¨horizontalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/menclose»«/mfrac»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«/math»
زمن حركة أيون الهيليوم أكبر بأربع مرات من زمن حركة أيون الهيدروجين.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«mi mathvariant=¨bold¨»TH«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle displaystyle=¨true¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«/mrow»«/mfrac»«/mstyle»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«/mfrac»«/math»
מטען ההליום ומטען המימן זהים בגודלם, מסת ההליום גדולה פי 4 ממסת המימן:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«mi mathvariant=¨bold¨»TH«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle displaystyle=¨true¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«/mrow»«/mfrac»«/mstyle»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle displaystyle=¨true¨ mathvariant=¨bold¨»«mfrac»«mrow»«menclose notation=¨horizontalstrike¨»«mn»2«/mn»«mo»§#183;«/mo»«mi»§#960;«/mi»«/menclose»«mo»§#183;«/mo»«mn»4«/mn»«mo»§#183;«/mo»«msub»«mi»m«/mi»«mi»H«/mi»«/msub»«/mrow»«menclose notation=¨downdiagonalstrike¨»«mi»B«/mi»«mo»§#183;«/mo»«msub»«mi»q«/mi»«mi»H«/mi»«/msub»«/menclose»«/mfrac»«/mstyle»«mfrac»«mrow»«menclose notation=¨horizontalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/menclose»«/mfrac»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«/math»
זמן תנועת יון ההליום גדול פי 4 מזמן תנועת יון המימן.
1. الأيونات متشابهة في شحنتها ولكنها تختلف في كتلتها. من التعبير عن زمن الدورة لشحنة تتحرك في حقل مغناطيسي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«/math»
من التعبير يمكن أن نرى أن زمن الدورة يتناسب طرديًا مع الكتلة. كتلة أيون الهيليوم أكبر بأربع مرات من كتلة أيون الهيدروجين. ولذلك فإن زمن دورة أيون الهيليوم أكبر بأربع مرات، وزمن حركته أكبر بأربع مرات.
2. السؤال يتعلق بالنسبة بين زمني حركة الأيونات وليس بالنسبة بين زمني الدورة.
قبل استخدام تعبير زمن الدورة، يجب توضيح أن النسبة بين زمني حركة الأيونات تساوي النسبة بين زمني الدورة.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«/math»
מהביטוי ניתן לראות שזמן המחזור תלוי ביחס ישר במסה . ליון ההליום מסה גדולה פי 4 ממסת יון המימן . לכן זמן המחזור של יון ההליום גדול פי 4. וזמן תנועתו גדול פי 4.
2. השאלה היא על יחס זמני תנועת היונים, ולא על יחס זמני המחזור .
לפני שמשתמשים בביטוי זמן המחזור יש להראות שיחס זמני תנועת היונים שווה ליחס זמני המחזור.
______________________________________________________________________________________
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»d«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»2«/mn»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«/msqrt»«/math»
البعد d يساوي الفرق بين قطري المسارين.
يمكن التعبير عن قطر كل مسار باستخدام تعبير نصف قطر مسار شحنة تتحرك في حقل مغناطيسي.
ניתן לבטא את הקוטר של כל מסלול בעזרת ביטוי לרדיוס המסלול של מטען הנע בשדה מגנטי.
البعد d يساوي الفرق بين قطري المسارين، نعبر عن البعد بدلالة نصفي قطري المسارين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»HE«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»H«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/math»
نعبر عن نصف قطر المدار من معادلة الحركة الدائرية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
تتحرك الشحنة بشكل عمودي على الحقل، والزاوية α تساوي 90 درجة. التعبير عن نصف قطر المسار:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»V«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»90«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«menclose notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
نعبر عن البعد d باستخدام تعبير نصف قطر مسار حركة الأيون:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/math»
يجب التعبير عن البعد d بدلالة فرق الجهد وليس بدلالة السرعة d .
للتمييز بين السرعة وفرق الجهد، نُشير إلى السرعة بالحرف V وفرق الجهد بـ - «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/math».
نستخدم قانون الشغل والطاقة للتعبير عن سرعة الأيونات بعد تسريعهما:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/menclose»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨/»«/math»
نعوِّض سرعة الأيونات بدلالة توتر التسريع، بتعبير البعد d:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«/mfrac»«/msqrt»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»HE«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mfrac»«/msqrt»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
مُعطى: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»HE«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»H«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»,«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»HE«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»H«/mi»«/msub»«/math» , نعوِّض في تعبير البعد d:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mfrac»«/msqrt»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
تبسيط جبري:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mfrac»«/msqrt»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»8«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«msqrt»«mfrac»«mrow»«msup»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«menclose notation=¨downdiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«menclose notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«menclose notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«msqrt»«mfrac»«mrow»«msup»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«menclose notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨horizontalstrike¨»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«menclose notation=¨horizontalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»d«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»2«/mn»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«/msqrt»«/menclose»«/math»
ولذلك، فإن التعبير البعد بين نقطتي إصابة الأيونين هو: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«/msqrt»«/math»
1. من المتبع الإشارة لفرق الجهد (التوتر) بـ «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«/math» أو U , في السؤال، يشار إلى التوتر بالحرف V مثل السرعة من المهم جدًا استخدام رموز مختلفة
للسرعة وفرق الجهد. بالنسبة لأولئك الذين اعتادوا على استخدام الإشارة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«/math» من المفضل أن نُشير لفرق الجهد بـ «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«/math» على الرغم من أنه أشير له في نص السؤال بـ V.
للسرعة وفرق الجهد. بالنسبة لأولئك الذين اعتادوا على استخدام الإشارة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«/math» من المفضل أن نُشير لفرق الجهد بـ «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«/math» على الرغم من أنه أشير له في نص السؤال بـ V.
2. الخطوة الجبرية في هذا السؤال طويلة ومرهقة بعض الشيء، إذا لم يتبقى الكثير من الوقت في الامتحان، فمن المستحسن عدم التبسيط جبريا.
يمكنك كتابة التعبير بدلالة المقادير الأربعة التي تظهر في السؤال والتوقف عند هذه المرحلة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mrow mathcolor=¨#FF0000¨»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»v«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»v«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mfrac»«/msqrt»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»H«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
3. من الممكن التوصل إلى تعبير السرعة V للشحنة المتسارعة ببدلالة فارق الجهد «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«/math» , حسب حفظ الطاقة الكلية:
نُشير إلى النقطة التي بدأت فيها الشحنة بالتسارع بـ O ونقطة نهاية التسارع بـ A:
دعونا نشير إلى الطاقة الوضعية بـ U، والفرق بالطاقة الوضعية بـ«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»OA«/mi»«/msub»«/math».
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»O«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#FF0000¨ notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«msub»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»O«/mi»«/msub»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»O«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»O«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»q«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»q«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#FF0000¨ notation=¨circle¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/msqrt»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»
למהירות ולמתח. למי שרגיל להשתמש בסימון U למתח מומלץ לסמן את המתח באות U למרות שהמתח מסומן באות V.
2. המהלך האלגברי בשאלה זו מעט ארוך ומסורבל , אם לא נשאר הרבה זמן בבחינה, מומלץ לא לפשט אלגברית.
רק לכתוב את הביטוי בתלות בארבעת הגדלים המופיעים בשאלה.
______________________________________________________________________________________
5. 2010,4- تتحرك كرة مشحونة داخل حقل مغناطيسي
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»44«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
القانون الأول لنيوتن.
تتحرك الكرة في خط مستقيم في اتجاه أفقي، حسب القانون الأول لنيوتن فإن محصّلة القوى المؤثرة على الكرة في الاتجاه العمودي يساوي صفرًا.
وفقًا لاتجاه حركة الكرة واتجاه الحقل المغناطيسي، تؤثر قوة مغناطيسية للأعلى حسب قاعدة اليد اليسرى.
تؤثر قوة الجاذبية على الكرة نحو الأسفل.
نرسم مخطط اللقوى المؤثرة على الكرة:
لنكتب معادلة الحركة في الاتجاه العمودي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/math»
الزاوية بين اتجاه حركة الشحنة واتجاه الحقل المغناطيسي تساوي 90 درجة. نُعوّض قيمة الزاوية ونعبر عن السرعة V0:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»90«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»28«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»26«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»63«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»44«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
سرعة رمي الكرة هي 4.44 متر في الثانية.
בהתאם לכיוון תנועת הכדור וכיוון השדה המגנטי , מכלל יד שמאל פועל כוח מגנטי כלפי מעלה .
כוח הכובד פועל על הכדור כלפי מטה.
נערוך תרשים כוחות לכוחות הפועלים על הכדור:
נכתוב את משוואת התנועה בכיוון האנכי:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/math»
הזווית שבין כיוון תנועת המטען לכיוון השדה היא 90 מעלות. נציב את את ערך הזווית ונבטא את המהירות V0:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»90«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»28«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»26«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»63«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»44«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
מהירות זריקת הכדור היא 4.44 מטר לשנייה.
1. من مبادئ الديناميكا، يجب أن يكون محصّلة القوى العمودية صفراً. لذلك يجب أن تعمل القوة المغناطيسية للأعلى.
وفقا لقاعدة اليد اليسرى، فإن اتجاه القوة المغناطيسية يكون للأعلى.
يوصى بفحص مبادئ مختلفة لنفس النتيجة، حتى لو تم الفحص فكريًا فقط.
بالإضافة إلى حل الأسئلة، فإن عمليات التفكير هذه تعوّد الطالب على الملاحظة أكثر والتفكير أكثر، وهذا يمكن أن يغير الشخص
بالإضافة إلى حل الأسئلة، فإن عمليات التفكير هذه تعوّد الطالب على الملاحظة أكثر والتفكير أكثر، وهذا يمكن أن يغير الشخص
2. ليس للكرة سرعة عمودية، بل سرعة أفقية فقط، ولا توجد قوى تؤثر في الاتجاه الأفقي، وبالتالي لا تتغير السرعة الأفقية.
تستمر الكرة في التحرك بسرعة الرمي في الاتجاه الأفقي.
3. مكتوب في السؤال أنه تم رمي الكرة أفقيًا. لكنها ليست حركة باليستية في رمي أفقي.
בהתאם לכלל יד שמאל, כיוון הכוח המגנטי הוא כלפי מעלה.
מומלץ לבחון עקרונות שונים של אותה מסקנה , גם אם הבחינה נעשית בצורה מחשבתית בלבד.
מעבר לפתרון השאלות, תהליכי חשיבה כאלו מרגילים את הלומד להתבונן יותר ולחשוב יותר , זה יכול לשנות בן אדם.
2. לכדור אין מהירות אנכית רק מהירות אופקית, לא פועלים כוחות בכיוון האופקי לכן המהירות האופקית לא משתנה .
הכדור ממשיך לנוע במהירות הזריקה בכיוון האופקי.
3. כתוב בשאלה שהכדור נזרק אופקית. אך לא מדובר בתנועה בליסטית בזריקה אופקית.
______________________________________________________________________________________
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨16px¨»«mrow»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»79«/mn»«mi mathvariant=¨bold¨»S«/mi»«/mrow»«/mstyle»«/math»
تعبير زمن الدورة لحركة الشحنة في الحقل المغناطيسي.
تؤثر ثلاث قوى على الكرة: القوة العمودية لأعلى، وقوة الجاذبية لأسفل، والقوة المغناطيسية.
حسب اتجاه الحقل المغناطيسي واتجاه الحركة وفقًا لقاعدة اليد اليسرى، تعمل القوة المغناطيسية في اتجاه نحو نقطة مركز الدوران.
نرسم مخطط للقوى المؤثرة على الكرة:
نكتب معادلات الحركة في الاتجاه العمودي وفي الاتجاه المركزي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»
ومن ثم، تتحرك الكرة في مستوى عمودي على الحقل المغناطيسي «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/math», نعبر عن زمن الدورة من معادلة الحركة نحو المركز.
نستخدم تعبير السرعة الخطية بدلالة السرعة الزاوية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»90«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»§#969;«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»
الزمن المطلوب هو زمن دورة واحدة كاملة، ويمكن ايجاد هذا الزمن بمساعدة تعبير زمن الدورة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»Q«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»28«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»26«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»76«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»63«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»79«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»S«/mi»«/math»
زمن حركة الكرة في دورة الواحدة هو 2.79 ثانية.
בהתאם לכיוון השדה המגנטי ולכיוון התנועה לפי כלל יד שמאל הכוח המגנטי פועל בכיוון נקודת מרכז הסיבוב.
נערוך תרשים כוחות לכוחות הפועלים על הכדור:
נכתוב את משוואות התנועה לכיוון האנכי ולכיוון הרדיאלי:
1. قوة الجاذبية والقوة العمودية تُبطل احدهما الأخرى، فتتحرك الكرة بشكل مشابه لحركة الشحنة في حقل مغناطيسي.
2. من المهم جدًا معرفة كيفية تطوير تعبير زمن الدورة لشحنة تتحرك في حقل مغناطيسي.
في معادلة الحركة هناك سرعة خطية وسرعة زاوية، للوصول إلى تعبير زمن الدورة، يجب التعبير عن السرعة الخطية أولاً
بدلالة السرعة الزاوية. وإلا سيتم الحصول على التعبير التالي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»r«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msqrt mathcolor=¨#FF0000¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msqrt mathcolor=¨#FF0000¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msqrt mathcolor=¨#FF0000¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«/msqrt»«/math»
جبريًا التعبير صحيح، لكننا لا نطور هذا التعبير لزمن الدورة لأنه مضلل.
يبدو من التعبير أن زمن الدورة يتعلق على السرعة. لكنه لا يتعلق حقًا لأنه عندما تزيد السرعة، يزداد نصف قطر المسار أيضًا.
2. מאוד חשוב לדעת לפתח את ביטוי זמן המחזור של מטען הנע בשדה מגנטי.
במשוואת התנועה יש מהירות קווית ומהירות זוויתית, כדי להגיע לביטוי זמן המחזור יש לבטא קודם את המהירות הקווית
בתלות במהירות הזוויתית. אחרת יתקבל הביטוי הבא:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»r«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msqrt mathcolor=¨#FF0000¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msqrt mathcolor=¨#FF0000¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msqrt mathcolor=¨#FF0000¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«/msqrt»«/math»
אלגברית הביטי נכון, אבל אנחנו לא מפתחים את הביטוי הזה לזמן המחזור מכיוון שהוא מטעה.
מהביטוי נראה שזמן המחזור תלוי במהירות. אך הוא באמת לא תלוי מכיוון שכאשר המהירות גדלה גם רדיוס המסלול גדל.
______________________________________________________________________________________
______________________________________________________________________________________
...
الحقل المغناطيسي لا يبذل شغلًا، لأن القوة عمودية على الحركة.
تعريف الشغل.
تعمل القوة المغناطيسية بشكل عمودي على الحركة، من تعريف الشغل «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math» , القوة المغناطيسية لا تبذل شغلًا.
1. الحقل يسبب قوة. ولهذا السبب من المتّبع القول إن الحقل يؤثر بقوة أو أن الحقل يبذل شغلًا.
2. تعمل القوة المغناطيسية دائمًا بشكل عمودي على الحركة، وبالتالي لا تبذل شغلًا دائمًا. من قانون الشغل والطاقة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«/msub»«/math»
عندما لا يتم بذل أي شغل، لا يحدث تغيير في الطاقة الحركية، ولهذا السبب تتحرك الشحنة المتحركة في الحقل المغناطيسي بسرعة منتظمة.
2. הכוח המגנטי תמיד פועל בניצב לתנועה לכן הוא תמיד לא מבצע עבודה . ממשפט העבודה אנרגיה «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«/msub»«/math»
כאשר לא מבוצעת עבודה אין שינוי באנרגיה הקינטית , זאת הסיבה שמטען הנע בשדה מגנטי נע במהירות קצובה.
______________________________________________________________________________________
______________________________________________________________________________________
...
القوة المغناطيسية ليس لها مركّب في اتجاه موازٍ لقوة الجاذبية، فالقوة المغناطيسية تعمل بشكل عمودي على قوة الجاذبية.
متجهات
من قاعدة اليد اليسرى، وفقًا لاتجاه حركة الكرة واتجاه الحقل المغناطيسي، أن اتجاه القوة المغناطيسية يكون موازيًا للحقل، متعامدًا مع قوة الجاذبية.
ولذلك، فإن القوة المغناطيسية ليس لها أي مركّب في اتجاه القوة المغناطيسية.
לכן, אין לכוח המגנטי רכיב בכיוון כוח הכבוד.
1. من وجهة نظر متجهة، عندما يكون المتجه عموديًا على اتجاه معين، فإن المتجه لا يحتوي على مركّب في نفس الاتجاه.
في الشكل التالي، يتم وصف المتجه F الذي يعمل بزاوية بالنسبة لاتجاه المحور X بشكل عام.
نحلل المتجه F تحليلًا قائم الزاوية:
نعبر عن مركّب متجه F في اتجاه المحور X بشكل عام:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«/mrow»«/mstyle»«/math»
عندما يكون اتجاه المتجه F متعامدًا مع اتجاه المحور X، فإن المتجه لا يكون له أي مركّب في اتجاه المحور X:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«/mstyle»«/math»
2. في اتجاه موازي لقوة الجاذبية، أو ببساطة في اتجاه قوة الجاذبية.
3. في هذا القسم، تم استخدام قوة الجاذبية لوصف الاتجاه، غير اتجاه قوة الجاذبية، فإن قوة الجاذبية نفسها ليست ذات أهمية.
באיור הבא מתואר באופן כללי ווקטור F הפועל בזווית ביחס לכיוון הציר X .
נבצע הפרדה ישרת זווית לווקטור F:
נבטא את רכיב הווקטור F בכיוון ציר X , באופן כללי:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«/mrow»«/mstyle»«/math»
כאשר כיוון הווקטור F ניצב לכיוון ציר ה X , אין רכיב לווקטור בכיוון ציר ה X:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«/mstyle»«/math»
2. כיוון מקביל לכוח הכובד , זה במילים פשוטות כיוון כוח הכובד.
3. בסעיף זה נעשה שימוש בכוח הכובד כדי לתאר כיוון , מעבר לכיוון כוח הכובד אין כל חשיבות לכוח הכובד עצמו.
______________________________________________________________________________________
د.
______________________________________________________________________________________
...
كان زمن حركة الشحنة في الهواء هو نفسه، ولا تؤثر القوة المغناطيسية على حركتها العمودية.
مبدأ استقلالية الحركات.
ومن مبدأ استقلالية الحركات فإن زمن حركة الكرة يتعلق فقط على الحركة العمودية.
القوة المغناطيسية ليس لها أي تأثير على الحركة العمودية. ولذلك، إذا لم تكن هناك قوة مغناطيسية، فإن زمن حركة الشحنة في الهواء سيكون هو نفسه.
אין לכוח המגנטי השפעה על התנועה האנכית. לכן אם לא היה פועל כוח מגנטי זמן תנועת המטען באוויר היה זהה.
1. من حيث المبدأ، غالبًا ما يتم استخدام استقلالية الحركات في فصل الحركة المستوية في الميكانيكا، فمن المهم فهم المبادئ جيدًا من أجل
أن نتذكراستخدامها في كل سؤال يتعلق بهذا المبدأ.
2. لمساعدة الطالب في الإجابة على السؤال، تناول البند السابق حقيقة أن القوة المغناطيسية ليس لها مركّب في الاتجاه العمودي.
في هذا البند يجب أن نفهم أن القوة المغناطيسية ليس لها أي تأثير على الاتجاه العمودي.
שנזכור להשתמש בהם בכל שאלה שהעקרונות רלבנטיים אליה.
2. כדי לעזור לתלמיד לענות על השאלה , הסעיף הקודם עוסק בעובדה שאין לכוח המגנטי רכיב בכיוון האנכי.
בסעיף זה יש להבין שאין לכוח המגנטי השפעה על הכיוון האנכי.
______________________________________________________________________________________
6. 2010,5- الحقل المغناطيسي حول سلك مستقيم
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»MP«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»9«/mn»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«/mstyle»«/math»
إيجاد مقاومة المقاومة المتغيرة في الحالة الموصوفة، واستخدام مبادئ الدائرة على التوالي
تتكون الدائرة من مصدر جهد مثالي ومقاومة متغيرة وسلك مستقيم موصول على التوالي.
يتم توصيل المقاومة المتغيرة بتوصيل ريئوستاتي، طول المقاومة بأكملها 8 سم، ومقاومتها القصوى 20 أوم، نحسب مقاومة المقاومة لكل وحدة طول (المقاومة الطولية).
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#955;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»20«/mn»«mn mathvariant=¨bold¨»8«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#937;«/mi»«mi mathvariant=¨bold¨»cm«/mi»«/mfrac»«/math»
عندما يكون التماسّ المتحرك على بعد 2 سم من الطرف K، يمر التيار من الطرف L إلى التماسّ المتحرك من خلال 6 سم من المقاومة المتغيرة.
نحسب مقاومة المقاوم المتغير في هذه الحالة:: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#955;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»15«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/math».
في الدائرة الموصولة على التوالي، مجموع فروق الجهد على المستهلكين يساوي فرق جهد المصدر، وبالتالي فإن مجموع فروق الجهد على السلك والمقاومة يساوي جهد البطارية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MP«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«/mrow»«/mstyle»«/math»
نعبر عن فرق الجهد على السلك، ونحسب قيمته باستخدام المعطيات الموجودة في السؤال:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MP«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MP«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»24«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»15«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
وبالتالي فإن الجهد على السلك MP يساوي 9 فولط.
הנגד המשתנה מחובר בחיבור של ריאוסטט , אורך כל הריאוסטט 8 ס"מ . והתנגדותו המקסימאלית 20 אום. נחשב את התנגדות הריאוסטט ליחידת אורך.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#955;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»20«/mn»«mn mathvariant=¨bold¨»8«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#937;«/mi»«mi mathvariant=¨bold¨»cm«/mi»«/mfrac»«/math»
כאשר המגע הנייד נמצא במרחק 2 ס"מ מהקצה K , הזרם עובר מהקצה L למגע הנייד דרך 6 ס"מ של הנגד המשתנה.
נחשב את התנגדות הנגד המשתנה במצב זה: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#955;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»15«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/math».
במעגל טורי ,סכום המתחים על הצרכנים שווה למתח המקור .לכן סכום המתחים על התיל ועל הריאוסטט שווה לכא"מ הסוללה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MP«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«/mrow»«/mstyle»«/math»
נבטא את המתח על התיל, ונחשב את ערכו בעזרת נתוני השאלה:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MP«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MP«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»24«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»15«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
לכן, המתח על התיל MP שווה ל 9 וולט.
يتم وصف موقع التماسّ المتحرك من خلال جزء المقاومة المتغيرة الذي لا يتدفق فيه التيار.
يجب تحديد مقاومة المقاومة المتغيرة وفقًا للجزء من المقاومة المتغيرة الذي يتدفق من خلاله التيار.
יש לקבוע את התנגדות הנגד המשתנה בהתאם לחלק הנגד המשתנה דרכו זורם הזרם.
______________________________________________________________________________________
______________________________________________________________________________________
...
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨»I«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»66«/mn»«mi mathvariant=¨bold¨»A«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mi mathvariant=¨bold¨»min«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»82«/mn»«mi mathvariant=¨bold¨»A«/mi»«/mstyle»«/math»
إيجاد مقاومة السلك وحساب قيمة التيار عندما تكون المقاومة المحصّلة في قيمتها القصوى وعندما تكون في قيمتها الدنيا.
يكون التيار ذو قيمة قصوى عندما يكون التماسّ المتحرك في النقطة L وتكون المقاومة المحصّلة في قيمتها الصغرى.
نحسب القيمة القصوى للتيار من قانون أوم على الدائرة بأكملها في هذه الحالة:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»max«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MP«/mi»«/msub»«/mfrac»«/mstyle»«/math»
ولإيجاد مقاومة السلك نستخدم قانون أوم على السلك حسب القسم السابق:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MP«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»MP«/mi»«/msub»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»9«/mn»«mn mathvariant=¨bold¨»1«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
نعوّض مقاومة السلك في تعبير التيار الأقصى:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»max«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»24«/mn»«mn mathvariant=¨bold¨»9«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»66«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
يكون التيار في قيمته الصغرى عندما تكون قيمة المقاومة المحصّلة قصوى. وتكون المقاومة القصوى عندما يكون التماسّ المتحرك في الطرف K.
حساب القيمة الصغرى للتيار:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»min«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»LK«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MN«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»24«/mn»«mrow»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»82«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
شدة التيار الصغرى هو 0.82 أمبير، والقيمة القصوى لشدة التيار هي 2.66 أمبير.
נחשב את עוצמת הזרם מחוק אום על כל המעגל במצב זה:
1. على الرغم من أن السؤال يتناول الحقل المغناطيسي، إلا أن البندين الأولين يتعاملان فقط بموضوع الدائرة الكهربائية.
2. لا يمكن ايجاد التيار دون حساب مقاومة السلك أولاً.
2. לא ניתן למצוא את הזרם בלי לחשב קודם את התנגדות התיל.
______________________________________________________________________________________
______________________________________________________________________________________
...
رسم الرسم البياني وفقا للمعطيات الموجودة في الجدول.
وفقًا للمعطيات الموجودة في الجدول، سنقوم برسم رسمً بيانيًا يمثل الحقل المغناطيسي كدالة للتيار:
ومن المهم أن نُشير إلى الوحدات على المحاور، والإنتباه إلى أن وحدات المحور العمودي معطاة بالميكرو تسلا.
______________________________________________________________________________________
ج. 
______________________________________________________________________________________
...
ميل الرسم البياني يساوي 3.75 ميكرو تسلا لكل أمبير.
حساب ميل خط الاتجاه.
يجب حساب ميل الرسم البياني بناءً على نقطتين تقعان على خط الاتجاه.
يبدو من الرسم البياني أن خط الاتجاه يمر بالنقطة الأولى والأخيرة، نحسب ميله وفقًا لهاتين النقطتين:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1513;§#1497;§#1508;§#1493;§#1506;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»I«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»75«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/msup»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»A«/mi»«/mfrac»«/mrow»«/mstyle»«/math»
ميل الرسم البياني يساوي 3.75 ميكرو تسلا لكل أمبير.
מהגרף נראה שהישר המסתבר ביותר עובר דרך הנקודה הראשונה והאחרונה, נחשב את השיפוע בהתאם לנקודות אלו:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1513;§#1497;§#1508;§#1493;§#1506;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»I«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»75«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/msup»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»A«/mi»«/mfrac»«/mrow»«/mstyle»«/math»
שיפוע הגרף הוא 3.75 מיקרו טסלה לאמפר.
1. حتى لو لم يكن مكتوبا في السؤال "اكتب وحدات الميل". اكتب دائمًا وحدات الميل بعد كتابة قيمة الميل.
2. من المهم الانتباه إلى أن قيم الحقل المغناطيسي هي بوحدات ميكرو تسلا، وليس تسلا.
2. חשוב לשים לב שערכי השדה המגנטי הוא ביחידות של מיקרו טסלה , ולא טסלה.
______________________________________________________________________________________
ج. 
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨»d«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«mi mathvariant=¨bold¨»cm«/mi»«/mrow»«/mstyle»«/math»
التعبير عن الحقل المغناطيسي بالقرب من سلك مستقيم.
نُطوّر تعبيرًا لشدة الحقل المغناطيسي بدلالة البعد عن السلك (الدالة الموصوفة في الرسم البياني).
نستخدم التعبير عن الحقل المغناطيسي بالقرب من سلك موصل مستقيم:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/mrow»«/mstyle»«/math»
من الدالة، تعبير ميل الرسم البياني: «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«/mfrac»«/mstyle»«/math» , نقارن تعبير ميل الرسم البياني مع قيمته:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»75«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/msup»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»75«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»75«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»053«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/mstyle»«/math»
وبالتالي، فإن البعد بين السلك والنقطة N هي 5.3 cm.
נשתמש בביטוי השדה המגנטי בסביבת מוליך ישר :
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/mrow»«/mstyle»«/math»
מהפונקציה ,ביטוי שיפוע הגרף הוא: «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«/mfrac»«/mstyle»«/math» , נשווה בין ביטוי שיפוע הגרף לבין ערכו:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»75«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/msup»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»75«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»75«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»053«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/mstyle»«/math»
לכן, המרחק בין הנקודה התיל לנקודה N , היא 5.3 ס"מ.
1. يصف الجدول قيم التيار والحقل المغناطيسي على التوالي في خمسة قياسات.
بمساعدة التعبير عن الحقل المغناطيسي حول سلك موصل مستقيم،رياضيًا يمكن حساب البعد d من كل قياس.
من الناحية الفيزيائية، ليس من الصحيح التوصل إلى نتيجة من قياس واحد وعدم الأخذ بالحسبان جميع القياسات الأخرى.
بما أن المعطيات الموجودة في الجدول مبنية على تجربة، يوجد خطأ في القياس العشوائي في كل قياس، فمن الخطأ استخلاص النتيجة
على أساس قياس واحد.
يتم تحديد خط الاتجاه وفقًا للقياسات الخمسة جميعها في عملية مشابهة لعملية المتوسط الحسابي.
وبما أن أخطاء القياس عشوائية، فإن المتوسط يقلل من الأخطاء العشوائية بشكل كبير.
يجب أن تعتمد الإجابة الصحيحة والكاملة على هذا القسم على ميل الرسم البياني وليس على قياس واحد.
2. في الأسئلة التي يوجد بها رسم بياني، من المهم جدًا تطوير تعبير للدالة المعطاة في الرسم البياني، وفي كثير من الأحيان يتم ايجاد الإجابة بواسطة الميل.
בעזרת ביטוי השדה המגנטי בסביבת מוליך ישר מתמטית ניתן לחשב מכל מדידה את המרחק d.
פיזיקלית לא נכון להגיע למסקנה ממדידה אחת ולא להתייחס לכל המדידות האחרות.
מכיוון שנתוני הטבלה מבוססים על ניסוי קיימת שגיאת מדידה אקראית בכל מדידה, לא נכון להגיע למסקנה
על סמך מדידה אחת.
הישר המסתבר ביותר נקבע בהתאם לכל חמשת המדידות בפעולה הדומה לפעולת מיצוע.
מכיוון ששגיאות המדידה הן אקראיות, המיצוע מקטינים את השגיאות האקראיות בצורה משמעותית.
תשובה נכונה ומלאה לסעיף חייבת להתבסס על שיפוע הגרף ולא על מדידה אחת.
2. מאוד חשוב לפתח ביטוי לפונקציה הנתונה בגרף, הרבה פעמים התשובה נמצאת בשיפוע.
______________________________________________________________________________________
______________________________________________________________________________________
...
لن يتغير ميل الرسم البياني. وهو يتعلق فقط على البعد بين النقطة N والسلك.
استخدام تعبير الميل.
من تعبير ميل الرسم البياني «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«/mfrac»«/mstyle»«/math» الميل يتعلق ببعد النقطة N من السلك
لا يتغير هذه البعد نتيجة لتغيير السلك الموصل، وبالتالي لا يتغير ميل الرسم البياني.
לכן שיפוע הגרף לא משתנה.
אם התיל MP יוחלף בתיל אחר בעל שטח חתך גדול יותר, מביטוי התנגדות התיל «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#961;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«mi mathvariant=¨bold¨»A«/mi»«/mfrac»«/math» התנגדות התיל החדש
תהיה יותר קטנה. ההתנגדות השקולה תהיה יותר קטנה הזרם יהיה יותר גדול, אך המרחק d לא משתנה ההתנגדות של התיל
1. يتم قياس البعد r في تعبير الحقلل المغناطيسي من مركز السلك، ولا يتعلق بعد النقطة من السلك على قطر السلك.
2. إذا تم استبدال سلك MP بسلك آخر مساحة مقطعه العرضي أكبر، من تعبير مقاومة السلك «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»§#961;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«mi mathvariant=¨bold¨»A«/mi»«/mfrac»«/math» مقاومة السلك الجديد
تكون أصغر. وستكون المقاومة المحصّلة أصغر، وسيكون التيار أكبر، لكن البعد d لا يتغير، وبالتالي يكون الميل ثابتًا.
3. السؤال يتعلق بميل الرسم البياني، لذلك يجب استخدام تعبير ميل الرسم البياني للإجابة على السؤال.
لا يمكن الإجابة على العديد من الأسئلة بالمنطق العام، ويجب استخدام المبادئ بشكل منهجي، وهذا القسم مثال على ذلك.
הוא ממרכז קוטר התיל זניח ביחס למרחק שבין התיל לנקודה. החלפת התיל לא משנה את מרחק
______________________________________________________________________________________
7. 2008,4- تتحرك شحنة في أربع مناطق مُربعة الشكل
______________________________________________________________________________________
...
الشحنة سالبة، وفقًا لقاعدة اليد اليسرى .
قاعدة اليد اليسرى على الشحنة عندما تدخل المنطقة 4.
نحدّد إشارة الشحنة حسب اتجاه القوة المؤثرة عليها عند دخولها المنطقة 4.
اتجاه متجه الحقل المغناطيسي نحو الخارج، واتجاه متجه السرعة إلى اليمين، واتجاه متجه القوة المغناطيسية نحو مركز الدوران.
نُضيف متجه السرعة ومتجه القوة إلى الشكل:
اتجاه المتجهات الثلاثة يتوافق مع قاعدة اليد اليسرى مع قاعدة اليد اليمنى، وبالتالي فإن الشحنة المتحركة هي شحنة سالبة.
כיוון ווקטור השדה המגנטי הוא החוצה, כיוון ווקטור המהירות ימינה וכיוון וקטור הכוח המגנטי פועל לכיוון נקודת מרכז הסיבוב.
נוסיף לאיור את וקטור המהירות ואת ווקטור הכוח :
כיוון שלושת הווקטורים מתאים לכלל יש שמאל עם יד ימין , לכן המטען הנע הוא מטען שלילי.
1. يجب تحديد المتجهات على الحقل المغناطيسي، وعندها فقط نستخدم قاعدة اليد اليسرى.
وهكذا يصبح من الأسهل ايجاد الإجابة الصحيحة، وأن نكون أكثر ثقة بها.
2. يجب تحديد إشارة الشحنة من حركة الشحنة في المنطقة 4، لأن اتجاه الحقل المغناطيسي محدّد في هذه المنطقة فقط.
يمكنك استخدام قاعدة اليد اليسرى لأي نقطة تتحرك فيها الشحنة، ومن الأسهل استخدام قاعدة اليد اليسرى في لحظة الدخول أو الخروج من المنطقة.
3. يجب تحديد اتجاه القوة المغناطيسية حسب شكل المسار، القوة المغناطيسية هي القوة الجاذبة المركزية التي تعمل نحو نقطة مركز الدوران.
في الشكل التالي، يتم تحديد نقطة مركز الدوران ومتجه القوة المغناطيسية.
4. عند استخدام قاعدة اليد اليسرى لا داعي لوصف اتجاهات الأصابع، يكفي التفسير بشكل عام "وفقا لقاعدة اليد اليسرى".
כך יותר קל למצוא את התשובה הנכונה , ולהיות יותר בטוחים בה.
2. יש ללמוד על סימן המטען מתנועת המטען באזור 4 , מכיוון שכיוון השדה המגנטי נתון רק באזור זה.
אפשר להשתמש בכלל יד שמאל לכל נקודה בה המטען נע , נוח להשתמש בכלל יש שמאל ברגע הכניסה או היציאה מהאזור.
3. את כיוון הכוח המגנטי יש לקבוע בהתאם לצורת המסלול, הכוח המגנטי הוא הכוח הצנטריפאלי
הפועל לכיוון נקודת מרכז הסיבוב. באיור הבא מסומנת נקודת מרכז הסיבוב ו- ווקטור הכוח המגנטי.
______________________________________________________________________________________
______________________________________________________________________________________
...
المنطقة 1 - اتجاه المجال للخارج.
المنطقة 2 - اتجاه المجال للداخل.
المنطقة 3 - اتجاه المجال للداخل.
אזור 2- כיוון השדה פנימה.
אזור 3- כיוון השדה פנימה.
إيجاد اتجاه الحقل المغناطيسي في كل منطقة حسب اتجاه الحقل في المنطقة 4 وحسب شكل المسار.
اعتمادا على شكل مسار الشحنة، عندما تتحرك الشحنة من المنطقة 3 إلى المنطقة 4 ينعكس اتجاه القوة، وبالتالي فإن اتجاه الحقل المغناطيسي في المنطقة 3 يكون عكس اتجاه الحقل المغناطيسي في المنطقة 4.
اتجاه الحقل المغناطيسي في المنطقة 4 هو للخارج، وبالتالي فإن اتجاه الحقل المغناطيسي في المنطقة 3 هو للداخل.
في المنطقة 2، تتجه القوة الجذب المركزية لنفس النقطة كما في المنطقة 3. وبالتالي، فإن اتجاه الحقل المغناطيسي في المنطقة 2 هو أيضًا نحو الداخل.
اتجاه القوة المغناطيسية المؤثرة على الشحنة في المنطقة 1 لحظة قبل دخولها المنطقة 2 يكون عكس اتجاه القوة المغناطيسية في المنطقة 2،
وبالتالي فإن اتجاه الحقل المغناطيسي في المنطقة 1 هو عكس اتجاه الحقل المغناطيسي في المنطقة 2. واتجاه الحقل المغناطيسي في المنطقة 1 هو إلى الخارج.
نضيف اتجاهات الحقول المغناطيسية إلى كل منطقة من المناطق في الشكل:
כיוון השדה המגנטי באזור 4 הוא החוצה, מכאן שכיוון השדה המגנטי באזור 3 הוא פנימה.
באזור 2 הכוח הצנטריפטלי פונה לאותה נקודה כמו באזור 3. לכן, כיוון השדה המגנטי באזור 2 הוא גם פנימה.
כיוון הכוח המגנטי הפועל על המטען באזור 1 רגע לפני כניסתו לאזור 2 הפוך לכיוון הכוח המגנטי באזור 2 ,
לכן כיוון השדה המגנטי באזור 1 הפוך לכיוון השדה המגנטי באזור 2. כיוון השדה המגנטי באזור 1 הוא החוצה.
נוסיף את כיווני השדות המגנטיים לכל אחד מהאזורים באיור:
1. بعد تحديد اتجاهات الحقول في المناطق الثلاث، من المهم التأكد من صحة التحديد في كل منطقة باستخدام قاعدة اليد اليسرى.
2. في المنطقة 1 والمنطقة 4 تعمل الحقول المغناطيسية في نفس الاتجاه نحو خارج الصفحة. على الرغم من اختلاف نقطة مركز الدوران في كل منطقة.
يرجع الاختلاف إلى حقيقة أن الشحنة لا تتحرك بشكل مستمر من المنطقة 1 إلى المنطقة 4.
2. באזור 1 ובאזור 4 השדות המגנטיים פועלים בכיוון זה כלפי מעלה. למרות שנקודת מרכז הסיבוב בכל אזור היא שונה.
השוני נובע מכך שהמטען לא נע ברציפות מאזור 1 לאזור 4 .
______________________________________________________________________________________
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨»C«/mi»«/math»
تعبير الشحنة من معادلة الحركة.
القوة الوحيدة المؤثرة على الشحنة هي القوة المغناطيسية، نرسم مخطط القوى للحظة دخول الشحنة للمنطقة 4:
نكتب معادلة الحركة الدائرية.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
تتحرك الشحنة باتجاه عمودي على الحقل المغناطيسي, «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»90«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#176;«/mo»«/math». نُعبّر عن الشحنة q من معادلة الحركة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»V«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»90«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«menclose notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»27«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»20«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»15«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/math»
الشحنة سالبة، لذلك: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/math»
הכוח היחיד הפועל על המטען הוא הכוח המגנטי, נערוך תרשים כוחות לרגע כניסת המטען לאזור 4:
נכתוב את משוואת התנועה המעגלית ,ונבטא ממנה את המטען.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
נשתמש
يتم الحصول على مقدار الشحنة من معادلة الحركة، وإشارة الشحنة سالبة. ومن المهم أن نذكر هذا في الجواب.
وفقا للمبادئ الفيزيائية، يمكن إضافة إشارة الطرح إلى الإجابة، حتى عندما تكون الإجابة موجبة رياضيا.
בהתאם לעקרונות הפיזיקליים ניתן להוסיף סימן מינוס לתשובה, גם כאשר מתמטית התשובה היא חיובית.
______________________________________________________________________________________
______________________________________________________________________________________
...
1. يتغير اتجاه السرعة - مسار الحركة ليس خطيًا.
2. لا يتغير مقدار متجه السرعة - فالقوة المغناطيسية هي الوحيدة التي تؤثر على الشحنة وتعمل بشكل عمودي على الحركة.
2. וקטור המהירות לא משתנה בגודלו - הכוח המגנטי ,הוא היחיד שפועל על המטען והוא פועל בניצב לתנועה.
فقط القوة المغناطيسية هي التي تؤثر، وهي متعامدة للحركة.
1. اتجاه متجه السرعة هو اتجاه الحركة. يتغير اتجاه الحركة وبالتالي يتغير اتجاه متجه السرعة.
2. القوة الوحيدة المؤثرة في كل منطقة من المناطق الأربع هي القوة المغناطيسية المتعامدة مع الحركة، ولا تبذل القوة المغناطيسية شغلًا.
ولذلك، لا يتغير مقدار متجه السرعة.
2. הכוח היחיד הפועל בכל אחד מארבעת אזורים הוא הכוח המגנטי הניצב לתנועה , הכוח המגנטי לא מבצע עבודה .
לכן ווקטור מהירות לא משתנה בגודלו.
1. القوة المغناطيسية تعمل دائما في اتجاه الحركة فهي تؤثر على اتجاه الحركة ولا تؤثر على مقدار السرعة.
2. من المهم أن نفهم أن المقادير المتجهة لها مقدار واتجاه ولا تتعلق ببعضها البعض.
2. חשוב להבין שלגדלים וקטוריים יש גודל ויש כיוון והן אינם תלויים האחד בשני.
______________________________________________________________________________________
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨»S«/mi»«/math»
تطوير تعبير زمن الدورة من معادلة الحركة.
من لحظة دخول الشحنة إلى المنطقة 1 في النقطة P حتى خروجها من المنطقة 4 في النقطة Q، تتحرك الشحنة في أربعة أرباع الدورة.
الزمن الذي تستغرقه الشحنة للانتقال من النقطة P إلى النقطة Q هو زمن دورة كاملة.
نُطوّر تعبير زمن الدورة من معادلة الحركة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»
تتحرك الكرة في مستوى عمودي على الحقل المغناطيسي، لذلك : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/math», نُعبّر عن زمن الدورة من معادلة الحركة نحو المركز.
نُعبّر عن السرعة الخطية كدالة للسرعة الزاوية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»90«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»§#969;«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
نُعوّض معطيات الجسيم (أ) والحقل المغناطيسي. ونجد زمن الدورة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»27«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»19«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»26«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»S«/mi»«mspace linebreak=¨newline¨»«/mspace»«/math»
ولذلك، فإن زمن حركة الشحنة هو «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«mspace linebreak=¨newline¨/»«/math» ثانية.
זמן תנועת המטען מנקודה P לנקודה Q הוא זמן מחזור שלם.
נפתח את ביטוי זמן המחזור ממשוואת התנועה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»
הכדור נע במישור הניצב לשדה המגנטי לכן «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/math», נבטא את זמן המחזור ממשוואת התנועה הצנטריפטאלית.
נבטא את המהירות הקווית בתלות במהירות הזוויתית:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»90«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»§#969;«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
נציב את נתוני חלקיק א' והשדה המגנטי . ונמצא את זמן המחזור:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»27«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»19«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»26«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»S«/mi»«mspace linebreak=¨newline¨»«/mspace»«/math»
לכן, זמן תנועת המטען הוא «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«mspace linebreak=¨newline¨/»«/math» שניות.
1. زمن حركة الجسيم A داخل الحقل المغناطيسي صغير جدًا. للوهلة الأولى تبدو أن الإجابة خاطئة.
وبعد التفكير مرة أخرى، تبلغ سرعة الجسيم 3.6 مليون متر في الثانية، والأبعاد صغيرة جدًا، وبالتالي فإن زمن الدورة صغير جدًا.
2. يمكن ايجاد زمن الدورة من مبادئ الحركة الدائرية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«mi mathvariant=¨bold¨»V«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»15«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»10«/mn»«mrow mathcolor=¨#FF0000¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»S«/mi»«/math»
במחשבה שנייה, מהירות החלקיק היא 3.6 מיליון מטר לשנייה והמרחקים מאוד קטנים לכן זמן המחזור מאוד קטן.
2. ניתן למצוא את זמן המחזור מעקרונות התנועה המעגלית:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«mi mathvariant=¨bold¨»V«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»15«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»10«/mn»«mrow mathcolor=¨#FF0000¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»S«/mi»«/math»
______________________________________________________________________________________
______________________________________________________________________________________
...
سيتحرك الجسيم C على طول المسار وفقًا لقاعدة اليد اليسرى.
قاعدة اليد اليسرى.
نُضيف إلى الرسم البياني متجه السرعة ومتجه القوة المغناطيسية عندما يدخل الجسيم عند النقطة Q ويتحرك في نفس المسار في الاتجاه المعاكس.
وفقا لاتجاهات متجهات السرعة والقوة المغناطيسية والحقل المغناطيسي. لكي يتحرك الجسيم على طول المسار، حسب اليد اليسرى يجب أن تكون موجبة.
في البند (أ) وجدنا أن شحنة الجسيم "أ" سالبة.
وفقًا لما ورد في السؤال، فإن الجسيم "ب" له نفس شحنة الجسيم أ، والجسيم "ج" له شحنة معاكسة لشحنة الجسيم "أ".
لكي يتحرك الجسيم المشحون على طول المسار، يجب أن تكون شحنته موجبة، وبالتالي فإن الجسيم الذي سيتحرك على طول المسار هو الجسيم "ج".
בהתאם לכיווני ווקטורי המהירות, הכוח המגנטי והשדה המגנטי . כדי שהחלקיק ינוע לאורך המסלול, מכלל יד שמאל עם יד שמאל
צריך להיות חיובי.
בסעיף א' מצאנו שמטען חלקיק א' הוא שלילי.
בהתאם לנאמר בשאלה לחלקיק ב' יש מטען זהה לחלקיק א', לחלקיק ג' יש מטען מנוגד למטען חלקיק א' .
כדי שהחלקיק הטעון ינוע לאורך המסלול מטענו צריך להיות חיובי , לכן החלקיק שינוע לאורך המסלול הוא חלקיק ג'.
1. السؤال يحتوي على الكثير من الكلمات، هناك ثلاث شحنات، "ب" يشبه "أ"، "ج" مختلف. عليك أن تفهم بالضبط ما هو السؤال بعبارات بسيطة.
السؤال هو ما هي الإشارة التي يجب أن تكون للشحنة حتى تتمكن من التحرك في نفس المسار في الاتجاه المعاكس.
2. يمكن استخدام قاعدة اليد اليسرى للشحنتين اللتين تدخلان المجال "ب" - السالبة. "ج" - الموجبة، ومعرفة أي منهم سوف يتحرك على طول المسار.
3. عندما يتحرك جسيم في الاتجاه المعاكس يتغير اتجاه سرعته وحتى لا يتغير اتجاه القوة فيجب تغيير إشارة الشحنة.
השאלה היא מה צריך להיות הסימן של מטען כדי שהוא יוכל לנוע באותו מסלול בכיוון ההפוך.
2. ניתן להשתמש בכלל יד שמאל עבור שני המטענים הנכנסים לשדה ב'- שלילי. ג' - חיובי , ולראות מי מהם ינוע לאורך המסלול.
3. כאשר חלקיק נע בכיוון ההפוך כיוון המהירות משתנה כדי שכיוון הכוח לא ישתנה ,יש לשנות את סימן המטען.
______________________________________________________________________________________
8. 2007,4- شحنة تتحرك في حقل كهربائي وحقل مغناطيسي EK
______________________________________________________________________________________
...
أ - ممكن. عندما تتحرك الشحنة في اتجاه الحقل المغناطيسي أو في الاتجاه المعاكس للحقل المغناطيسي.
ب - غير ممكن. عندما تكون الشحنة في حالة سكون لا تؤثر أي قوة مغناطيسية، ستتحرك الشحنة من السكون تحت تأثير القوة الكهربائية.
ב- לא אפשרי. כאשר המטען נח לא פועל כוח מגנטי , המטען ינוע ממנוחה בהשפעת הכוח החשמלי.
قوة مغناطيسية تؤثر على شحنة متحركة في حقل مغناطيسي.
أ- ممكن - من التعبير عن القوة المغناطيسية المؤثرة على شحنة متحركة في حقل مغناطيسي «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math»
عندما تتحرك الشحنة باتجاه الحقل «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/math» تكون القوة المغناطيسية مساوية لصفر.
حتى عندما تتحرك الشحنة في الاتجاه المعاكس للحقل «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»180«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#176;«/mo»«/math» تكون القوة المغناطيسية مساوية لصفر.
ب - غير ممكن - تؤثر القوة المغناطيسية فقط على شحنة متحركة، وعندما تكون الشحنة في حالة سكون فإن القوة الكهربائية فقط هي التي تؤثر.وبالتالي ستتحرك الشحنة ولن تبقى ساكنة.
כאשר המטען נע בכיוון השדה «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/math» והכוח המגנטי שווה לאפס.
גם כאשר המטען נע בכיוון הפוך לשדה «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»180«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#176;«/mo»«/math» הכוח המגנטי שווה לאפס.
ב- לא אפשרי - כוח מגנטי פועל רק על מטען נע , כאשר המטען נח יפעל רק כוח חשמלי שקול הכוחות יהיה שונה מאפס.
1. في الحالة الموصوفة في البند ب، ستتحرك الجسيمات في اتجاه الحقل الكهربائي أو في الاتجاه المعاكس للحقل (إذا كانت الشحنات سالبة).
فمنذ اللحظة التي تبدأ فيها الجسيماات بالتحرك، سوف تؤثر قوة مغناطيسية في اتجاه عمودي على الحركة، فيتغير اتجاه الحركة، ويتغير اتجاه القوة المغناطيسية.
حتى لو كانت هناك لحظة تكون فيها القوة المغناطيسية والقوة الكهربائية متساوتين ومتعاكستين وتكون محصلتهما صفر - فلن تكون الشحنة في حالة سكون! انما ستستمر في حركتها !
2. ينص القانون الأول لنيوتن على أنه إذا كانت محصلة القوى تساوي الصفر، فإن الجسم يكون الجسم في حالة استمرارية. يمكن للجسم أن يكون ساكنًا أو يتحرك.
القانون الأول لا يفرق بين الحركة والسكون. والتفسير بواسطة القانون الأول لهذا القسم هو تفسير غير صحيح.
3. في التخطيط (أ)، تظهر الجسيمات التي تتحرك في حقل مغناطيسي، لكنلا توجد علاقة للتخطيط بالبندين الأولين.
מרגע תחילת תנועת החלקיקים יפעל כוח מגנטי בכיוון ניצב לתנועה כיוון התנועה ישתנה, וכיוון הכוח המגנטי ישתנה.
גם אם יהיה רגע שבו הכוח המגנטי והכוח החשמלי יהיה זהה ונגדי ושקול הכוחות יתאפס- המטען לא ינוח! הוא ימשיך לנוע!
2. החוק הראשון של ניוטון קובע שאם שקול הכוחות שווה לאפס הגוף מתמיד בתנועתו. גוף מתמיד יכול לנוע או לנוח.
החוק הראשון לא מבחין בין תנועה למנוחה. נימוק על פי החוק הראשון לסעיף זה הוא נימוק לא נכון.
______________________________________________________________________________________
______________________________________________________________________________________
...
الجسيم 1 - موجب. وفقا لقاعدة اليد اليسرى.
الجسيم 2- سالب. وفقا لقاعدة اليد اليسرى.
חלקיק 2- שלילי . בהתאם לכלל יד שמאל עם יד ימין.
قاعدة اليد اليسرى.
اتجاه الحقل المغناطيسي هو "خارج" من الصفحة، حيث يتحرك كلا الجسيمين إلى اليمين على الشحنة 1، تؤثر القوة المغناطيسية نحو الأسفل،
وعلى الشحنة 2 تؤثر القوة المغناطيسية نحو الأعلى. كما هو مبين في التخطيط التالي:
حسب قاعدة اليد اليسرى فإن الشحنة 1 موجبة.
حسب قاعدة اليد اليسرى فإن الشحنة 2 سالبة.
על מטען 2 פועל כוח מגנטי כלפי מעלה.
כלל יד שמאל עם יד שמאל מתאים למטען 1 - לכן מטען 1 הוא חיובי.
כלל יד שמאל עם יד ימין מתאים למטען 2 - לכן מטען 2 הוא שלילי.
1. مكتوب في السؤال أنه مبيّن جزأين من مساري هذين الجسيمين معروضين، في التخطيط جزاي المسارين مختلفين - لا يمكن التعرف على نوع الشحنة !
2. في بعض الأسئلة يتم وصف الحقل الموجه من الصفحة نحو الخرج بالنقاط، وفي بعض الأسئلة بالنقاط المحاطة بالدوائر. عليك أن تعرف كلا النموذجين.
2. בחלק מהשאלות שדה שכיוונו החוצה מהדף מתואר בעזרת נקודות , ובחלק מהשאלות נקודות המוקפות בעיגולים.
______________________________________________________________________________________
______________________________________________________________________________________
...
من معادلة الحركة يمكن التوصل إلى التعبير عن مقدار الشحنة: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#969;«/mi»«/mrow»«mi mathvariant=¨bold¨»B«/mi»«/mfrac»«/math» , ومن هذا التعبير يمكن ملاحظة أن الشحنتين متساويتان في المقدار.
التعبير لمقدار الشحنة من معادلة الحركة الدائرية.
يتحرك الجسيمان في حركة دائرية منتظمة تحت تأثير القوة المغناطيسية وحدها.
سنكتب معادلة الحركة بدلالة السرعة الزاوية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»
نكتب السرعة الخطية كدالة للسرعة الزاوية
والتعبير عن شحنة الجسيم من معادلة الحركة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»§#969;«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«menclose notation=¨updiagonalstrike¨ mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#969;«/mi»«/mrow»«mi mathvariant=¨bold¨»B«/mi»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»
من التعبير الذي تم الحصول عليه يمكن ملاحظة أنه إذا تحركت شحنتان لهما نفس الكتلة بنفس السرعة الزاوية في نفس الحقل المغناطيسي، كلا الجسيمين لهما نفس الشحنة.
נכתוב את משוואת התנועה, בתלות במהירות הזוויתית:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»
נכתוב את המהירות הקווית בתלות במהירות הזוויתית
ונבטא ממשוואת התנועה את מטען החלקיק:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»§#969;«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«menclose notation=¨updiagonalstrike¨ mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#969;«/mi»«/mrow»«mi mathvariant=¨bold¨»B«/mi»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»
מהביטוי שהתקבל ניתן לראות שאם שני מטענים בעלי מסה זהה ,נעים במהירות זוויתית זהה באותו שדה שדה מגנטי,
מטעני החלקיקים זהים בגודלם.
1. من مبادئ الديناميكا يجب رسم مخطط القوى لكل جسم على حدة. وبناء على ذلك أكتب معادلات الحركة على الجسم.
وبما أن كلا الجسيمين يتحركان بحركة دائرية في الحقل المغناطيسي، فيمكن الإجابة على السؤال من خلال معادلة عامة تصف مقدار شحنة الجسيمات المشحونة التي تتحرك في حركة دائرية في حقل مغناطيسي.
2. يمكن الوصول إلى تعبير الشحن من تعبير زمن الدورة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»90«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathcolor=¨#000000¨ mathvariant=¨bold¨»2«/mn»«mo mathcolor=¨#000000¨ mathvariant=¨bold¨»§#183;«/mo»«mi mathcolor=¨#000000¨ mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mi mathcolor=¨#000000¨ mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathcolor=¨#000000¨ mathvariant=¨bold¨»§#969;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»B«/mi»«/mfrac»«/math»
מכיוון ששני החלקיקים נעים בתנועה מעגלית בשדה המגנטי, ניתן לענות על השאלה ממשוואה כללית המתארת
את גודל המטען של חלקיקי טעון הנע בתנועה מעגלית בשדה מגנטי.
2. ניתן להגיע לביטוי המטען מביטוי זמן המחזור :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»90«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathcolor=¨#000000¨ mathvariant=¨bold¨»2«/mn»«mo mathcolor=¨#000000¨ mathvariant=¨bold¨»§#183;«/mo»«mi mathcolor=¨#000000¨ mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mi mathcolor=¨#000000¨ mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathcolor=¨#000000¨ mathvariant=¨bold¨»§#969;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»B«/mi»«/mfrac»«/math»
______________________________________________________________________________________
______________________________________________________________________________________
...
تحديد محور أصله في نقطة بداية الحركة، وتطوير تعبير للطاقة الحركية بدلالة الموقع.
نصف حركة الجسيم بالنسبة إلى محور الحركة الذي أصله في نقطة بداية الحركة واتجاهه في اتجاه الحركة.
خارج اللوحين يتحرك الجسيم تحت تأثير القوة المغناطيسية فقط، وسرعة الجسيم لا تتغير في المقدار، والطاقة الحركية ثابتة.
يتحرك الجسيم بين اللوحين في حقل كهربائي متجانس، وبتسارع ثابت، تتغير الطاقة الحركية.
تتعلق الطاقة في كل نقطة على مربع السرعة. سنكتب تعبير مربع السرعات بالنسبة لمحور الحركة المحدّد:
الموقع الإبتدائي يساوي الصفر. وبالتالي فإن الإزاحة تساوي الموقع النهائي، ويتحقق:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/math»
نعبر عن الطاقة الحركية بين اللوحان كدالة لـ X:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«msup»«mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mspace linebreak=¨newline¨»«/mspace»«mo»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/math»
نعبر عن تسارع الجسيم كدالة للقوة الكهربائية، من القانون الثاني لنيوتن :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»F«/mi»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
نعبر عن القوة الكهربائية باستخدام تعريف الحقل:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
نعبر عن شدة الحقل الكهربائي كدالة لفرق الجهد V:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨ mathcolor=¨#000000¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#000000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#000000¨»V«/mi»«/mrow»«mi mathvariant=¨bold¨ mathcolor=¨#000000¨»d«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
نعوّض المعطيات في تعبير الطاقة الحركية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mi mathvariant=¨bold¨»d«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mi mathvariant=¨bold¨»d«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1000«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»16«/mn»«/mrow»«/msup»«/mrow»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
وفقًا لهذا التعبير،نحسب الطاقة الحركية للجسيم عندما يصل إلى النقطة H:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»16«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/math»
عندما يغادر الجسيم النقطة H، فإنه يستمر في الحركة بنفس الطاقة الحركية.
נתאר את תנועת החלקיק ביחס לציר תנועה שראשיתו בנקודת תחילת התנועה וכיוונו ככיוון התנועה.
מחוץ ללוחות החלקיק נע בהשפעת כוח מגנטי בלבד, מהירות החלקיק לא משתנה בגודלה, האנרגיה הקינטית קבועה .
בין הלוחות החלקיק נע בשדה חשמלי אחיד, בתאוצה קבועה, האנרגיה הקינטית משתנה.
האנרגיה תלויה בכל נקודה בריבוע המהירות. נכתוב את ביטוי ריבוע המהירויות ביחס לציר התנועה הנבחר:
המיקום ההתחלתי שווה לאפס. לכן העתק שווה למיקום הסופי, ומתקיים:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/math»
נבטא את האנרגיה הקינטית בין הלוחות בתלות ב X:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«msup»«mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mspace linebreak=¨newline¨»«/mspace»«mo»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/math»
1. عندما يكون الجسيم بين اللوحين فإن سرعته تزداد بدلالة الزمن بشكل قطع مكافئ وفقا لما يلي: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msup»«/math»
تتغير الطاقة الحركية لجسم يتحرك بتسارع ثابت بصورة خطية مع الموقع. من المستغرب بعض الشيء ...
2. من التعبير عن الطاقة الحركية للجسيم بين اللوحين بدلالة الموقع: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»X«/mi»«/math» يمكن ملاحظة أن الطاقة الحركية تتعلق خطيًا على الموقع. بدلًا منتطوير تعبير للطاقة الحركية بدلالة الموقع وفقًا لمعطيات السؤال، يمكن حساب الطاقة الحركية للجسيم عند وصوله إلى اللوح H، وذلك بالاستعانة بقانون الشغل والطاقة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»10«/mn»«mrow mathcolor=¨#FF0000¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»1000«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»10«/mn»«mrow mathcolor=¨#FF0000¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»16«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»J«/mi»«/math»
وبالتالي، لا يمكن رسم الرسم البياني إلا من حساب الطاقة الحركية للجسيم عندما يمر عبر النقطة H.
دون تطوير تعبير للطاقة الحركية بدلالة الموقع طبقاً لمعطيات السؤال.
האנרגיה הקינטית של גוף הנע בתאוצה קבועה , משתנה בצורה ליניארית בתלות במקום. קצת מפתיע....
2.אפשר לפתח את ביטוי האנרגיה הקינטית בתלות במקום בעזרת משפט העבודה אנרגיה...
3. סימן האנרגיה הקינטית חייב להיות חיובי.
______________________________________________________________________________________
9. 2007,5- ايجاد المركب الأفقي للحقل المغناطيسي الأرضي بواسطة ملف طويلة
______________________________________________________________________________________
...
التخطيط (ج).
جمع متجهات.
في الرسم البياني (ب)، يتم الإشارة من إبرة البوصلة عند عدم تدفق تيار في الدائرة. في هذه الحالة يكون اتجاه إبرة البوصلة نحو الشمال الجغرافي.
من قاعدة اليد اليمنى، وفقًا لاتجاه التيار، يكون اتجاه الحقل المغناطيسي على طول محور الملف إلى اليسار. (لاتجاه الغرب).
نرسم رسم تخطيطي للمركّب الأفقي للحقل المغناطيسي الأرضي - BE. بالنسبة للحقل المغناطيسي الناتج عن التيار - BI والحقل المغناطيسي المحضّل - B.
حالة الانحراف الملائمة لظروف التجربة هي الحالة الموصوفة في التخطيط (ج).
מכלל יד ימין , בהתאם לכיוון הזרם כיוון השדה המגנטי לאורך ציר הסילונית הוא שמאלה. (בכיוון מערב).
נערוך תרשים לשדה המגנטי המגנטי הנוצר מכדור הארץ - BE. לשדה המגנטי הנוצר מהסילונית - BI ולשדה המגנטי השקול - B.
מצב הסטייה המתאים לתנאי הניסוי הוא המצב המתואר בתרשים ג'.
1. في البوصلة يكون للإبرة رأس سهم أو علامة للتمييز بين اتجاه الشمال واتجاه الجنوب.
الإبرة الموضحة في الرسم البياني لا تحتوي على علامة تميز بين الاتجاه الشمالي والجنوبي.
ينبغي التعرف على اتجاه الشمال من خلال الحرف "N" المكتوب أعلى البوصلة.
2. لعدد اللفات ليس له وحدات، كثافة اللفات لها وحدات، الوحدات عبارة عن مقلوب المتر.
3. كثافة اللفات تساوي النسبة بين عدد اللفات N على طول الملف L: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»n«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«/math».
تظهر صيغة حساب الحقل المغناطيسي في ملف طويل في ورقة القوانين:
لا يوجد تعبير لكثافة اللفّات، ويجب أن نتذكر أن النسبة بين عدد اللّفات وطول الملف تساوي كثافة الملف الطويل.
4. تتعلق كثافة اللفّات فقط على قطر السلك الموصل الذي يتكون منه الملف، وذلك وفقاً لما يلي: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»n«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»d«/mi»«/mfrac»«/math».
5. في أغلب الأحيان، في الأسئلة التي تتناول الحقل المغناطيسي للأرض، يجب حساب المركّب الأفقي لشدة الحقل المغناطيسي الأرضي.
في هذا السؤال يتم إعطاء المُركّب الأفقي للحقل المغناطيسي للأرض في السؤال.
6. اتجاه انحراف إبرة البوصلة لا يتعلق على شدة التيار، فقط على اتجاه التيار في الملف الطويل.
7. ليست هناك حاجة لوصف شكل استخدام قاعدة اليد اليمنى بالتفصيل. ويكفي في التفسير أن نذكُر استخدام قاعدة اليد اليمنى.
في الشكل التالي وصفاً تفصيلياً لاستخدام قاعدة اليد اليمنى لتحديد اتجاه الحقل المغناطيسي داخل على امتداد محور الملف الطويل:
8. لوصف الحقل المغناطيسي حول سلك موصل مستقيم، يجب استخدام اليد اليمنى بطريقة مختلفة، ويتم دراسة الموضوع بالتفصيل بالوحدة 47.
במחט המתוארת בתרשים לא קיים סימון המבחין בין כיוון הצפון לדרום.
יש ללמוד על כיוון הצפון מהאות "צ" הכתובה בקצהו העליון של המצפן.
2. לרוב, בשאלות העוסקות בשדה המגנטי של כדור הארץ יש לחשב את עוצמת השדה המגנטי.
בשאלה זו הרכיב האופקי של השדה המגנטי של כדור הארץ נתון בשאלה .
3. אין קשר בין עוצמת הזרם לכיוון סטיית מחט המצפן.
4. אין צורך לתאר בצורה מפורטת את צורת השימוש בכלל יד ימין . בנימוק מספיק לציין שנעשה שימוש בכלל יד ימין.
באיור הבא מופיע תיאור מפורט של השימוש בכלל יד ימין למציאת כיוון השדה המגנטי בתוך ציר הסילונית :
______________________________________________________________________________________
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»32«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»14«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#176;«/mo»«/math»
يجب الربط الهندسي بين الزاوية والحقول المغناطيسية.
نعبر هندسيًا عن العلاقة بين متجهي الحقل ومقداره الزاوية باستخدام دالة الظل (tan):
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»BI«/mi»«mi mathvariant=¨bold¨»BE«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle displaystyle=¨true¨»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«/mstyle»«mi mathvariant=¨bold¨»BE«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»BE«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«/mfrac»«/mrow»«/mstyle»«/math»
مُعطى في السؤال كثافة لفّات الملف، يتم تعريف الكثافة وفقًا للنسبة بين عدد اللفات N وطول الملف L:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#000000¨»N«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»BE«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#000000¨»L«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathcolor=¨#000000¨ mathvariant=¨bold¨»n«/mi»«/mrow»«mi mathvariant=¨bold¨»BE«/mi»«/mfrac»«/mrow»«/mstyle»«/math»
نحسب مقدار الزاوية α:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2000«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»256«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»628«/mn»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»628«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»32«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»14«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#176;«/mo»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
ومن ثم، فإن إبرة البوصلة سوف تنحرف بزاوية قدرها 32.14 درجة.
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»BI«/mi»«mi mathvariant=¨bold¨»BE«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle displaystyle=¨true¨»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«/mstyle»«mi mathvariant=¨bold¨»BE«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»BE«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«/mfrac»«/mrow»«/mstyle»«/math»
בשאלה נתונה צפיפות הכריכות של הסילונית , הצפיפות מוגדרת לפי היחס שבין מספר הכריכות N לאורך הסילונית L:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#000000¨»N«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»BE«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#000000¨»L«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathcolor=¨#000000¨ mathvariant=¨bold¨»n«/mi»«/mrow»«mi mathvariant=¨bold¨»BE«/mi»«/mfrac»«/mrow»«/mstyle»«/math»
נחשב את גודל הזווית α:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2000«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»256«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»628«/mn»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»628«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»32«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»14«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#176;«/mo»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
מכאן ,שמחט המצפן תסטה בזווית של 32.14 מעלות.
1. لربط الحقول المغناطيسية بالزاوية باستخدام دالة الظل، يجب أن يكون اتجاه الحقل المغناطيسي الناتج عن التيار متعامدًا مع اتجاه المركّب الأفقي للحقل المغناطيسي الأرضي،
(لا يمكن استخدام دالة الظل إلا في المثلث القائم الزاوية) .
2. يمكن أيضًا إجراء تجربة لإيجاد الحقل المغناطيسي باستخدام سلك موصل مستقيم أو ملف دائري رفيع.
في كل تجربة يتم الربط بين الحقول وزاوية الانحراف بمساعدة دالة الظل.
2. ניתן לבצע את הניסוי למציאת השדה המגנטי גם בעזרת מוליך ישר או סליל מעגלי דק .
בכל ניסוי הקשר בין השדות לזווית הסטייה נעשה בעזרת פונקציית הטנגנס.
______________________________________________________________________________________
______________________________________________________________________________________
...
سوف تزداد الزاوية α، لأن شدة الحقل المغناطيسي الناتج عن التيار في الملف تزداد.
الريوستات، قانون أوم للدائرة بأكملها. التعبير عن الحقل المغناطيسي الناتج عن الملف الطويل، ودالة الظل.
عندما يتم تحريك التماسّ المتحرك نحو الطرف N، ستنخفض مقاومة المقاومة المتغيرة، ومن قانون أوم ، فإن التيار في الدائرة سيزداد.
ومن التعبير عن الحقل المغناطيسي على طول المحور الملف الطويل، ستكون شدة الحقل المغناطيسي BI أكبر.
وحسب التعبير عن الزاوية: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»BI«/mi»«mi mathvariant=¨bold¨»BE«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math» ستزداد زاوية انحراف ابرة البوصلة.
في الكهرباء هناك أسئلة، للإجابة عليها، يجب فحص سلسلة من العلاقات. وهذا القسم خير مثال على ذلك.
يؤثر تغيير موقع التماسّ المتحرك على شدة التيار، وتؤثر شدة التيار على شدة الحقل المغناطيسي الناتج عن الملف.
وتؤثر شدة الحقل المغناطيسي الناتج عن الملف على زاوية الانحراف.
وتؤثر شدة الحقل المغناطيسي الناتج عن الملف على زاوية الانحراف.
للإجابة على هذا السؤال بشكل صحيح، يجب تنفيذ جميع السياقات بشكل صحيح، ويوصى بتكرار العملية بأكملها مرة أخرى
قبل الوصول إلى النتيجة النهائية.
قبل الوصول إلى النتيجة النهائية.
שינוי מיקום הגררה משפיע עוצמת הזרם, עוצמת הזרם משפיעה על עוצמת השדה המגנטי הנוצר מהסילונית.
ועוצמת השדה המגנטי הנוצר מהסילונית משפיע על זווית הסטייה.
כדי לענות נכון על שאלה זו יש לבצע את כל ההקשרים בצורה נכונה ,מומלץ לחזור על כל המהלך פעם נוספת
לפני שמגיעים למסקנה הסופית.
______________________________________________________________________________________
______________________________________________________________________________________
...
يجب أن يقع محور الملف في اتجاه الشمال والجنوب.
جمع المتجهات. يتم إنشاء الحقل المغناطيسي على طول محور الملف.
اتجاه المركّب الأفقي للحقل المغناطيسي الأرضي نحو الشمال.
لضبط هذا الحقل المغناطيسي لصفر، يجب وضع الملف بحيث يكون اتجاه الحقل المغناطيسي الناتج بالملف نحو الجنوب.
اتجاه الحقل المغناطيسي الناتج داخل الملف الطويل يكون على طول محور الملف. ولذلك، ينبغي وضع محور الملف في اتجاه الشمال والجنوب.
כדי לאפס שדה מגנטי זה יש למקם את הסילונית כך שכיוון השדה המגנטי הנוצר מהסילונית יהיה לכיוון דרום.
כיוון השדה המגנטי הנוצר מהסילונית הוא לאורך ציר הסילונית. לכן, יש למקם את הסילונית בכיוון צפון דרום.
1. حتى نجعل المركّب الأفقي للحقل المغناطيسي الأرضي صفرًا، لا يكفي أن يكون محور الملف في اتجاه الشمال والجنوب.
بالإضافة إلى ذلك، يجب تحديد اتجاه التيار وفقًا لقاعدة اليد اليمنى بحيث يكون الحقل المغناطيسي الناتج من الملف الطويل نحو الجنوب.
يتعامل البند فقط مع اتجاه محور الملف الذي يجعل المركّب الأفقي للحقل المغناطيسي صفرًا.
2. في المخططين (ج) و(د)، يظهر الاتجاه من الشمال إلى الجنوب عموديًا إلى داخل الصفحة، ولكن القصد هو الاتجاه الأفقي.
יש לקבוע את כיוון הזרם בהתאם לכלל יד ימין כך שהשדה המגנטי
______________________________________________________________________________________
______________________________________________________________________________________
...
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»7«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»95«/mn»«mi mathvariant=¨bold¨»mA«/mi»«/mrow»«/mstyle»«/math»
التعبير عن شدة الحقل المغناطيسي على طول محور الملف الطويل.
لجعل المركّب الأفقي للحقل المغناطيسي الأرضي صفرًا، على التيار المتدفق في الملف، إنشاء حقل مغناطيسي في الاتجاه المعاكس وتكون شدته مساوية للمركّب الأفقي للحقل المغناطيسي الأرضي.
نعبر عن شدة التيار حسب تعبير شدة الحقل المغناطيسي:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»n«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»B«/mi»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»n«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2000«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»51«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»95«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/math»
إن مقدار التيار اللازم لجعل المركّب الأفقي للحقل المغناطيسي الأرضي صفرًا هو 7.95 مللي أمبير.
נבטא את הזרם, מעוצמת ביטוי השדה המגנטי:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»n«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»B«/mi»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»n«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2000«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»51«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»95«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/math»
גודל הזרם המאפשר לאפס את הרכיב האופקי של השדה המגנטי הוא 7.95 מילי אמפר.
يصف تعبير الحقل المغناطيسي في مركز الملف الطويل مقدار الحقل المغناطيسي على طول محور الملف الطويل فقط.
المركّب الأفقي للحقل المغناطيسي الأرضي ثابت في كل نقطة في المنطقة التي أجريت فيها التجربة، وبالتالي حتى يصبح الحقل المحصّل صفرًا يكون ذلك على طول محور الملف فقط.
רכיב גודל השדה המגנטי הוא קבוע בכל נקודה באזור בו נעשה הניסוי , לכן הקיזוז הוא רק לאורך ציר הסילונית.
______________________________________________________________________________________