حلول التدريبات العملية في الحقل المغناطيسي: ח.4.2

70. ח.4.2

في البند ح.1.1 وجدنا شدة الحقل المغناطيسية التي يكونها السلك في كل من النقطتين B و- C.

«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/mstyle»«/math»

مقدار المركب الأفقي للحقل المغناطيسي للكرة الأرضية BE مساوٍ لـ - 30 ميكرو تسلا.

نحسب زاوية انحراف إبرة البوصلة في النقطة B:

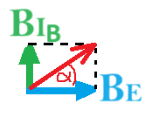
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»B«/mi»«msub»«mi mathvariant=¨bold¨»I«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«msub»«mi mathvariant=¨bold¨»B«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»B«/mi»«msub»«mi mathvariant=¨bold¨»I«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«msub»«mi mathvariant=¨bold¨»B«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»shift«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»shift«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»26«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»56«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#176;«/mo»«/mstyle»«/math»

نحسب زاوية انحراف البوصلة في النقطة C:

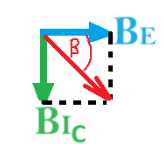
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«msub»«mi mathvariant=¨bold¨»B«/mi»«msub»«mi mathvariant=¨bold¨»I«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«/msub»«msub»«mi mathvariant=¨bold¨»B«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»shift«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«msub»«mi mathvariant=¨bold¨»B«/mi»«msub»«mi mathvariant=¨bold¨»I«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«/msub»«msub»«mi mathvariant=¨bold¨»B«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mrow»«mi mathvariant=¨bold¨»shift«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»=«/mo»«mrow»«mi mathvariant=¨bold¨»shift«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»45«/mn»«mo mathvariant=¨bold¨»§#176;«/mo»«/mrow»«/mstyle»«/math»

وبالتالي فإن زاوية ميل إبرة البوصلة الموجودة في النقطة B هي 26.56 درجة.

وزاوية ميل إبرة البوصلة الموجودة في النقطة C هي 45 درجة.