

______________________________________________________________________________________
...
نعم، لا توجد نقطة على طول المحور تكون فيها شدة الحقل صفرًا .
استعمال تعريف شدة الحقل «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#FF6600¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mfrac mathcolor=¨#FF6600¨»«mover»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨»q«/mi»«/mfrac»«/math». الحقل في أي نقطة على طول المحور يساوي مجموع متجهي الحقلين الناتجين بواسطة كل شحنة.
من تعريف الحقل الكهربائي «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mover»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨»q«/mi»«/mfrac»«/math» يكون الحقل الكهربائي صفر فقط في النقطة التي تكون فيها محصلة القوى الكهربائية المؤثرة على شحنة الفحص تساوي صفر.
إذا وضعنا شحنة فحص (شحنة موجبة وصغيرة) على المحور، بين الشحنتين، فإن الشحنتين ستؤثران بقوة على شحنة الفحص في اتجاه إلى اليمين، وستكون محصلة القوى المؤثرة على شحنة الفحص لا تساوي صفر.
في كل نقطة على يمين الشحنة السالبة وعلى يسار الشحنة الموجبة، ستؤثر الشحنتان قوى مختلفة الإتجاه والمقدار، لأن الشحنتين متساويتين في المقدار، ولكن بعد كل نقطة من الشحنتين في هذه المناطق يكون مختلفًا، فلا توجد نقطة يكون فيها محصلة القوى يساوي صفر.
ولذلك فمن تعريف الحقل لا توجد نقطة في حول الشحنتين يصبح فيها الحقل الكهربائي صفراً.
في نقطة اللانهاية (على جانبي المحور)، تكون شدة الحقل صفرًا.
אם נמקם מטען בוחן (מטען חיובי וקטן) על הציר, בין המטענים, שני המטענים יפעילו על מטען הבוחן כוח שכיוונו ימינה, שקול הכוחות הפועלים על מטען הבוחן יהיה שונה מאפס.
בכל נקודה מימין למטען השלילי ומשמאל למטען החיובי המטענים יפעילו כוחות שונים בכיוונם אך גם שונים בגודלם, מכיוון שהמטענים זהים בגודלם, ומרחק כל נקודה באזורים אלו מהמטענים הוא שונה, לא קיימת נקודה שבה שקול הכוחות שווה לאפס.
לכן, מהגדרת השדה לא קיימת נקודה בסביבת המטענים שבה השדה החשמלי מתאפס.
مكتوب في السؤال "على طول المحور X"، يمكن أن يكون المحور X لا نهائيًا، لذلك يمكن الإجابة على هذا السؤال في بطريقتين مختلفتين:
بالتطرق إلى محور لا نهائي - هناك نقطتان تكون فيهما شدة الحقل تساوي صفر.
بالتطرق إلى حول الشحنتين فقط - لا توجد نقطة تكون فيها شدة الحقل تساوي صفر.
בהתייחס לציר אינסופי - יש שתי נקודות בהן עוצמת השדה שווה לאפס.
בהתייחס לסביבת המטענים בלבד - לא קיימת נקודה שבה עוצמת השדה שווה לאפס.
______________________________________________________________________________________


______________________________________________________________________________________
...
نعم، في نقطة منتصف البُعد بين الشحنتين يكون الجهد صفرًا.
استخدام تعبير الجهد حول شحنة نقطية.
الجهد في أي نقطة على المحور تساوي المجموع العددي للجهودين الناتجين من الشحنتين على المحور.
הפוטנציאל בכל נקודה בציר שווה לסכום הסקלארי של הפוטנציאלים שהמטענים יוצרים בציר.
الجهد في أي نقطة يساوي مجموع الجهدين الناتجين من الشحنتين في هذه النقطة.
في نقطة منتصف البُعد بين الشحنتين، يتم تكوّن جهد موجب من الشحنة الموجبة وجهد سالب له نفس القيمة المطلقة من الشحنة السالبة.
ولذلك، في النقطة منتصف البُعد بين الشحنتين، يكون الجهد مساويًا لصفر.
نرى ذلك أيضًا بمساعدة عملية حسابية، حيث نُشير إلى نقطة المنتصف بين الشحنتين، النقطة A ونحسب الجهد في نقطة المنتصف:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»(«/mo»«mrow»«mo»-«/mo»«mi»q«/mi»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»v«/mi»«/mstyle»«/math»
בנקודת האמצע שבין המטענים, נוצר פוטנציאל חיובי מהמטען החיובי ופוטנציאל שלילי הזהה בערכו המוחלט מהמטען השלילי.
סכום הפוטנציאלים
1. الحقل والجهد وصفان مختلفان للحيّز حول الشحنة. يمكن أن تكون هناك حالة حيث يكون الجهد في نقطة ما مساويًا لصفر ويكون الحقل في تلك النقطة لا يساوي صفر. ويمكن أن تكون هناك حالة حيث يكون الحقل في نقطة ما مساويًا للصفر ويكون الجهد في تلك النقطة لا يساوي صفر.
2. الأسئلة التي تتناول النقطة التي يكون فيها الجهد والحقل مساويان لصفر هي أسئلة شائعة في أسئلة البجروت.
3. الحقل الكهربائي والقوة الكهربائية هما مقداران متجهان.
لحساب الحقل المحصل والقوة المحصلة في نقطة ما، يجب إجراء عملية جمع متجهي.
الجهد هو كمية عددية، لحساب الجهد في نقطة ما، يجب إجراء جمع عددي للجهدين في هذه النقطة.
2. שאלות שעוסקות בנקודה בה הפוטנציאל והשדה מתאפסים הן שאלות נפוצות בשאלות הבגרות.
3.השדה החשמלי והכוח החשמלי הם גדלים ווקטוריים.
כדי לחשב את השדה השקול בנקודה ואת הכוח השקול בנקודה יש לבצע פעולת חיבור ווקטורית.
הפוטנציאל הוא גודל סקלארי, כדי לחשב את הפוטנציאל בנקודה יש לבצע חיבור סקלארי בין הפוטנציאלים בנקודה.
שאלה חוזרת על עצמה.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨»W«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«/mfrac»«/mstyle»«/math»
تعبير شغل القوة الخارجية: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»E«/mi»«/mstyle»«/math».
من تعبير شغل القوة الخارجية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«/math» , شغل القوة الخارجية يساوي التغير في الطاقة الميكانيكية الكلية للشحنتين.
قبل تنفيذ الشغل، كانت الشحنتان في حالة سكون، وبعد تنفيذ الشغل بقيت الشحنتان في حالة سكون.
الشغل لا يسبب تغيرا في الطاقة الحركية، بل يسبب تغيرا في طاقة الوضع الكهربائية. ويتحقق: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«/math».
وفقا لذلك، نعبر عن عمل القوة الخارجية :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»(«/mo»«mrow»«mo»-«/mo»«mi»q«/mi»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«/mrow»«mi mathvariant=¨bold¨»d«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«mi mathvariant=¨bold¨»d«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»d«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»W«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«/mfrac»«/menclose»«mspace linebreak=¨newline¨/»«/math»
לפני ביצוע העבודה שני המטענים נמצאים במנוחה , בסיום ביצוע העבודה המטענים נמצאים במנוחה.
העבודה לא גורמת לשינוי בבאנרגיה הקינטית רק לשינוי באנרגיה הפוטנציאלית חשמלית. ומתקיים: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«/math».
נבטא בהתאם את עבודת הכוח החיצוני:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»(«/mo»«mrow»«mo»-«/mo»«mi»q«/mi»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«/mrow»«mi mathvariant=¨bold¨»d«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«mi mathvariant=¨bold¨»d«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»d«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»W«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«/mfrac»«/menclose»«mspace linebreak=¨newline¨/»«/math»
מכיוון שלפני ביצוע העבודה המטענים
1. الشغل المبذول لزيادة البعد بين الشحنتين يُبذَل ضد القوة الكهربائية بواسطة قوة غير حافظة.
من مبادئ الميكانيكا، ينص التعبير عن شغل قوة غير حافظة على أن شغل القوة الغير حافظة يساوي التغير في الطاقة الميكانيكية. يظهر التعبير في صفحات القوانين:
2. الطاقة الميكانيكية الكلية تساوي مجموع الطاقة الحركية والطاقة الوضعية للشحنتين: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«/math»
في هذه الحالة يجب بذل الشغل فقط لزيادة البعد بين الشحنتين، دون تغيير الطاقة الحركية للشحنتين.
التغير في الطاقة الميكانيكية يساوي في هذه الحالة التغير في الطاقة الوضعية: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«/math»
3. الصورة العامة للطاقة الوضعية لشحنتين نقطيتين متجاورتين هي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#FF0000¨ notation=¨box¨»«mi mathvariant=¨bold¨»U«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»Q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»Q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»r«/mi»«/mfrac»«/menclose»«/mstyle»«/math»
מעקרונות המכניקה, ביטוי עבודת הכוח הלא משמר קובע שעבודת הכוח לא משמר שווה לשינוי באנרגיה המכנית. הביטוי מופיע בדפי הנוסחאות:
2. האנרגיה המכנית הכוללת שווה לסכום האנרגיה הקינטית והפוטנציאלית של שני המטענים: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«/math»
במקרה זה, יש לבצע עבודה רק כדי להגדיל את המרחק בין המטענים, מבלי לשנות את האנרגיה הקינטית של המטענים.
השינוי באנרגיה המכנית שווה במקרה זה לשינוי באנרגיה הפוטנציאלית: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«/math»
3. בדפי הנוסחאות לא מופיע ביטוי לאנרגיה פוטנציאלית חשמלית של שני מטענים.
מופיע ביטוי לאנרגיה פוטנציאלית כובדית:
האנרגיה הפוטנציאלית של גופים נמשכים היא שלילית ושל גופים נדחים היא חיובית.
הצורה הכללית של האנרגיה הפוטנציאלית של שני מטענים סמוכים היא:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»Q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»Q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»r«/mi»«/mfrac»«/math»
______________________________________________________________________________________

 ______________________________________________________________________________________
______________________________________________________________________________________
...
الكرة A مشحونة بشحنة سالبة والكرة B مشحونة بشحنة موجبة.
وفقًا لاتجاه القوة التي يؤثر بها الحقل على الإلكترونات، من الممكن معرفة إشارة شحنة كل من الكرتين.
حسب تعريف الحقل: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mover»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨»q«/mi»«/mfrac»«/math» بما أن شحنة الإلكترونات سالبة، فإن الحقل يؤثر بقوة على "الإلكترونات الحرة" الموجودة داخل الكرتين، في الاتجاه المعاكس لاتجاه الحقل، إلى اليسار. ستنتقل الإلكترونات من الكرة B إلى الكرة A.
نظرًا لأنه قبل تشغيل الحقل، لم تكن الكرتان مشحونتان، ونتيجة لتشغيل الحقل A، سيكون لديها فائض من الإلكترونات وستكون مشحونة بشحنة سالبة، أما الكرة B فسوف يكون بها نقص في الإلكترونات وستكون مشحونة بشحنة موجبة.
מכיוון שלפני פעולת השדה הכדורים לא היו טעונים, כתוצאה מפעולת השדה בכדור A יהיה עודף אלקטרונים הוא יטען במטען שלילי, בכדור B יהיה חוסר באלקטרונים הוא יטען במטען חיובי.
1. لا توجد علاقة بين البندين الأولين وهذا البند.
2. عندما تتواجد داخل الحقل شحنة سالبة، على سبيل المثال شحنة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»C«/mi»«/math»، من تعريف الحقل، فإن اتجاه القوة التي ستؤثر على الشحنة يكون عكس اتجاه الحقل: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mfrac mathcolor=¨#FF0000¨»«mover»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«/math».
وعندما تتواجد داخل الحقل شحنة موجبة، على سبيل المثال شحنة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»C«/mi»«/math»، من تعريف الحقل، فإن اتجاه القوة التي ستؤثر على الشحنة يكون في اتجاه الحقل: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mover»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«/math».
3. مكتوب في السؤال أن الكرتين موصلتين، أي أنهما مصنوعتان من مواد موصلة، وفيهما "إلكترونات حرة" يمكنهم التحرك بين الكرتين.
في الكرات غير الموصلة (العازلة)، تكون كمية الإلكترونات الحرة ضئيلة.
إذا استبدلنا الكرتين الموصلتين بكرتين عازلتين وكرّرنا العملية، فلن يتم شحن الكرتين.
4. إذا أُخرجت الكرتان من داخل الحقل وكانتا متلامستين، وبعد ذلك تم فصلهما خارج الحقل، فلن تُشحنا في نهاية العملية.
ولكي يتم شحن الكرتين في نهاية العملية، يجب فصلهما وهما داخل الحقل.
5. تسمى عملية الشحن بمساعدة الحقل الكهربائي بالشحن بواسطة الحث.
2. כאשר בתוך השדה נמצא מטען שלילי, לדוגמה מטען של «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»C«/mi»«/math», מהגדרת השדה כיוון הכוח שיפעל על המטען הוא נגדי לכיוון השדה : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mfrac mathcolor=¨#FF0000¨»«mover»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«/math».
וכאשר בתוך השדה נמצא מטען חיובי, לדוגמה מטען של «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»C«/mi»«/math» ,מהגדרת השדה כיוון הכוח שיפעל על המטען הוא בככיוון השדה : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mover»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«/math».
3. הכדורים הם מוליכים, הכוונה שהם עושיים מחומרים מוליכים יש להם "אלקטרונים חופשיים" שיכולים לנוע בין הכדורים.
בכדורים לא מוליכים (מבודדים) כמות האלקטרונים החופשיים היא זניחה.
אם נחליף את הכדורים המוליכים בכדורים מבודדים ונחזור על התהליך , הכדורים לא יטענו.
הכדורים לא יטענו.
4. אם הכדורים יוצאו מהשדה כשהם נוגדעים אחד בשני, ויופרדו רק מחוץ לשדה , הם לא ישארו טעונים בסוף התהליך.
כדי שהכדורים יהיו טעונים גם בסוף התהליך יש להפריד ביניהם בתוך השדה.
הפרדה מחוץ לשדה. טעינה על ידי השראה. מטען שלילי
______________________________________________________________________________________
جـ .


______________________________________________________________________________________
...
لن يتم شحن الكرتين.
اعتمادًا على اتجاه القوة التي يؤثر بها الحقل على الإلكترونات، من الممكن معرفة إشارة شحنة كل من الكرتين.
في هذه الحالة، فإن اتجاه القوة الكهربائية التي تعمل على "الإلكترونات الحرة" في الكرتين سيكون عكس اتجاه الحقل للأسفل.
لن تتحرك الإلكترونات بين الكرتين لذا ستبقيان متعادلتان.
אלקטרונים לא ינועו בין הכדורים לכן הם ישארו ניטרליים.
1. يبدو أن الفرق بين هذا البند والبند ج.1 هو اختلاف بسيط، ولكنه بالغ الأهمية من حيث عملية الشحن.
يختبر محررو الأسئلة الفهم وليس المعرفة، وهذا القسم خير مثال على ذلك.
2. الكرتان موجودتان داخل الحقل وتكونان مستقطبان وغير مشحونتان. عندما يتم إخراجهما من داخل الحقل ستكونان غير مستقطبان وغير مشحونان.
כותבי השאלות בוחנים הבנה ולא ידע , סעיף זה הוא דוגמה טובה לכך.
2. כל הכדורים נמצאים בתוך השדה הם יהיו מקוטבים ולא טעונים. כאשר הם יוצאו מהשדה הם יהיו לא מקוטבים ולא טעונים.
______________________________________________________________________________________







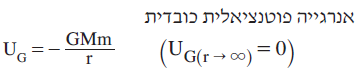

 ______________________________________________________________________________________
______________________________________________________________________________________
