15. 1997,1 - تقترب شحنة لكرة مشحونة.

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»12«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»57«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mstyle»«/math»
كتابة معادلة حفظ الطاقة والتعبير عن سرعة الإصابة من معادلة حفظ الطاقة.
نُشير إلى النقطة التي أصاب بها الإلكترون سطح القشرة بـ - B.
أثناء حركة الإلكترون من النقطة A إلى النقطة B، فإن القوة الكهربائية فقط هي التي تبذل شغل على الإلكترون، لذا يتم حفظ الطاقة الميكانيكية.
نكتب معادلة حفظ الطاقة ونعبر منها عن سرعة الإلكترون في النقطة B .
نرمز للجهد بـ - «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math» وللسرعة بـ - «math style=¨font-family:stix¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math».
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«/mstyle»«/math»
يبدأ الإلكترون بالحركة من حالة السكون، وتكون الطاقة الحركية للإلكترون في النقطة A صفرًا:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«msub»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«/mstyle»«/math»
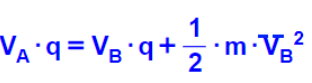

نحسب الجهد في النقطة A والنقطة B (على سطح القشرة):
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»Q«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»90«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»450«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»Q«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»90«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»900«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
نُعوّض في تعبير السرعة كتلة الإلكترون وشحنته والجهد في كل من النقطتين A وB:

בתנועת האלקטרון מנקודה A לנקודה B רק כוח חשמלי מבצע עבודה על האלקטרון, לכן האנרגיה המכנית נשמרת.
נכתוב את משוואת שימור האנרגיה ונבטא ממנה את מהירות האלקטרון בנקודה B.
נסמן את הפוטנציאל ב- «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math» ואת המהירות ב- «math style=¨font-family:stix¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math».
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«/mstyle»«/math»
האלקטרון מתחיל לנוע ממנוחה, האנרגיה הקינטית של האלקטרון בנקודה A היא אפס:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«msub»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«/mstyle»«/math»
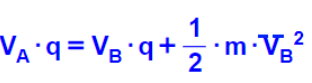

נחשב את הפוטנציאל בנקודה A ובנקודה B (על פני הקליפה):
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»Q«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»90«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»450«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»Q«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»90«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»900«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
נציב בביטוי המהירות את מסת האלקטרון, מטענו והפוטנציאלים בנקודות A ו- B :

1. قبل كتابة معادلة حفظ الطاقة، من الضروري معرفة سبب حفظ الطاقة الميكانيكية.
يتم حفظ الطاقة لأن القوة الكهربائية فقط هي التي تبذل شغل (القوة الكهربائية هي قوة حافظة).
2. تم تحديد النقطة التي تم فيها تحرير الإلكترون وهي النقطة A، ولم يتم تحديد نقطة إصابة الإلكترون سطح القشرة، حتى نتمكن من استخدام معادلة حفظ الطاقة
يجب تحديد نقطة الإصابة، وفي الحل المقترح في هذا البند تم الإشارة لنقطة الإصابة على أنها النقطة B.
يجب تحديد نقطة الإصابة، وفي الحل المقترح في هذا البند تم الإشارة لنقطة الإصابة على أنها النقطة B.
3. كتلة الإلكترون وشحنته موجودتان في ملحق أوراق القوانين.
4. هناك العديد من الأسئلة التي تستخدم فيها معادلة حفظ الطاقة لحساب سرعة شحنة متحركة (تحت تأثير القوة الكهربائية فقط) بين نقطتين.
האנרגיה נשמרת מכיוון שרק הכוח חשמלי מבצע עבודה.
2.הנקודה בה משוחרר האלקטרון מוגדרת כנקודה A , נקודת פגיעת האלקטרון לא מוגדרת , כדי שנוכל להשתמש במשוואת שימור האנרגיה
יש להגדיר את נקודת הפגיעה, בפתרון המוצע בסעיף זה נקודת הגידה מוגדרת כנקודה B.
3. מסת האלקטרון ומטענו נתונים בדפי הנוסחאות.
4. קיימות שאלות רבות בהן נעשה שימוש במשוואת שימור האנרגיה לחישוב מהירותו של מטען הנע (בהשפעת הכוח החשמלי בלבד) בין שתי נקודות.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»500«/mn»«mfrac»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/math»
استعمال تعبير الحقل المتجانس «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»-«/mo»«mfrac mathcolor=¨#FF6600¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«/mfrac»«/math».
تنطبق معادلة حفظ الطاقة أيضًا على الحقل المتجانس. ولذلك، فإن تعبير السرعة الذي حصلنا عليه في البند السابق مناسب أيضًا للحركة في حقل متجانس.
من التعبير يمكن ملاحظة أن السرعة في هذه الحالة تتعلق فقط بفرق الجهد بين نقطة بداية الحركة ونهايتها.
نحسب بمساعدة تعبير مقدار الحقل المتجانس شدة الحقل المتجانس الذي يتغير فيه الجهد بمقدار فرق الجهد الذي يتغير فيه في البند السابق (450 فولط) وعلى نفس البعد (10 سم).
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»|«/mo»«mrow»«mo»§#8710;«/mo»«mi»V«/mi»«/mrow»«mo stretchy=¨true¨»|«/mo»«/mstyle»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»|«/mo»«mrow»«mo»§#8710;«/mo»«mi»X«/mi»«/mrow»«mo stretchy=¨true¨»|«/mo»«/mstyle»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»450«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»500«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/math»
إذا تحرك الإلكترون في حقل متجانس، بين نفس فرق الجهد، وعلى نفس البُعد، فإن سرعة الإلكترون سوف تتغير بنفس المقدار.
מהביטוי ניתן לראות שמהירות במקרה זה תלויה רק בהפרש הפוטנציאלים שבין נקודת תחילת התנועה לסיום התנועה.
נחשב בעזרת ביטוי לגודל שדה אחיד את עוצמת השדה האחיד שבו הפוטנציאל משתנה בהפרש הפוטנציאלים בו הוא משתנה בסעיף
הקודם (450 וולט) ובמרחק זהה (10 ס"מ).
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨»«mo stretchy=¨true¨»|«/mo»«mi»E«/mi»«mo stretchy=¨true¨»|«/mo»«/mstyle»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»450«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»500«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/math»
אם האלקטרון ינוע בתוך שדה אחיד, בין אותו הפרש פוטנצילאים , ולאורך אותו מרחק, המהירות של האלקטרון תשתנה באותה מידה.
1. معادلة تغيير الطاقة في الميكانيكا تربط بين الارتفاعات والسرعات.
ومعادلة حفظ الطاقة في الكهرباء الساكنة تربط الجهد بالسرعات.
ومعادلة حفظ الطاقة في الكهرباء الساكنة تربط الجهد بالسرعات.
2. مادامت الشحنة تتحرك تحت تأثير القوة الكهربائية فقط فإن الطاقة الميكانيكية ستحفظ سواء تحركت الشحنة في حقل متفاوت الشدة أو في حقل متجانس.
3. تعبير الحقل المتجانس هو: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«/mfrac»«/math» وبما أنه يجب حساب شدة الحقل فقط، فيمكن أخذ القيمة المطلقة للحقل في عين الاعتبار «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mrow mathcolor=¨#FF0000¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»|«/mo»«mi mathvariant=¨bold¨»E«/mi»«mo stretchy=¨true¨ mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»|«/mo»«mrow»«mo»§#8710;«/mo»«mi»V«/mi»«/mrow»«mo stretchy=¨true¨»|«/mo»«/mstyle»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»|«/mo»«mrow»«mo»§#8710;«/mo»«mi»X«/mi»«/mrow»«mo stretchy=¨true¨»|«/mo»«/mstyle»«/mfrac»«/math».
4. يمكن أيضًا حل السؤال بمساعدة قانون الشغل والطاقة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«/msub»«/math»
وبما أن الحقل متجانس، فإن القوة المؤثرة على الإلكترون ثابتة، ويمكن التعبير عنها من تعريف الحقل: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mover mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mover»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨»q«/mi»«/mfrac»«/mstyle»«/math»
نكتب قانون الشغل والطاقة باستخدام تعبير القوة الكهربائية من تعريف الحقل الكهربائي، بما أن الإلكترون يتحرك من حالة السكون
اتجاه القوة هو نفس اتجاه الحركة :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«/msub»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«/msub»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«msub»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«/msub»«/math»
يتحرك الجسم من حالة السكون، وتكون طاقة حركته الابتدائية صفرًا. يمكن التعبير عن شدة الحقل من مبدأ الشغل والطاقة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«msub»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»`«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold-italic¨ mathcolor=¨#FF0000¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mstyle displaystyle=¨true¨»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«/mstyle»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«msup»«mo mathvariant=¨bold¨»`«/mo»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mstyle mathvariant=¨bold¨ displaystyle=¨true¨»«mi»m«/mi»«mo»§#183;«/mo»«mi»V«/mi»«msup»«mo»`«/mo»«mn»2«/mn»«/msup»«/mstyle»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mstyle mathvariant=¨bold¨ displaystyle=¨true¨»«mn»9«/mn»«mo».«/mo»«mn»1«/mn»«mo»§#183;«/mo»«msup»«mn»10«/mn»«mrow»«mo»-«/mo»«mn»31«/mn»«/mrow»«/msup»«mo»§#183;«/mo»«msup»«mfenced»«mrow»«mn»12«/mn»«mo».«/mo»«mn»57«/mn»«mo»§#183;«/mo»«msup»«mn»10«/mn»«mn»6«/mn»«/msup»«/mrow»«/mfenced»«mn»2«/mn»«/msup»«/mstyle»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»437«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»16«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»20«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»,«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»500«/mn»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«/math»
ומשוואת שימור האנרגיה באלקטרוסטטיקה מקשרת בין פוטנציאלים למהירויות.
2. כל עוד מטען נע בהשפעת כוח חשמלי בלבד האנרגיה המכנית נשמרת, בין אם המטען נע בשדה משתנה בעוצמתו או בשדה אחיד.
3. ביטוי השדה אחיד הוא: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«/mfrac»«/math» מכיוון שיש לחשב את רק עוצמת השדה ניתן להתייחס ערך המוחלט של השדה «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathvariant=¨bold¨ mathcolor=¨#FF0000¨»«mo stretchy=¨true¨»|«/mo»«mi»E«/mi»«mo stretchy=¨true¨»|«/mo»«/mstyle»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«/mfrac»«/math»
______________________________________________________________________________________
______________________________________________________________________________________
...
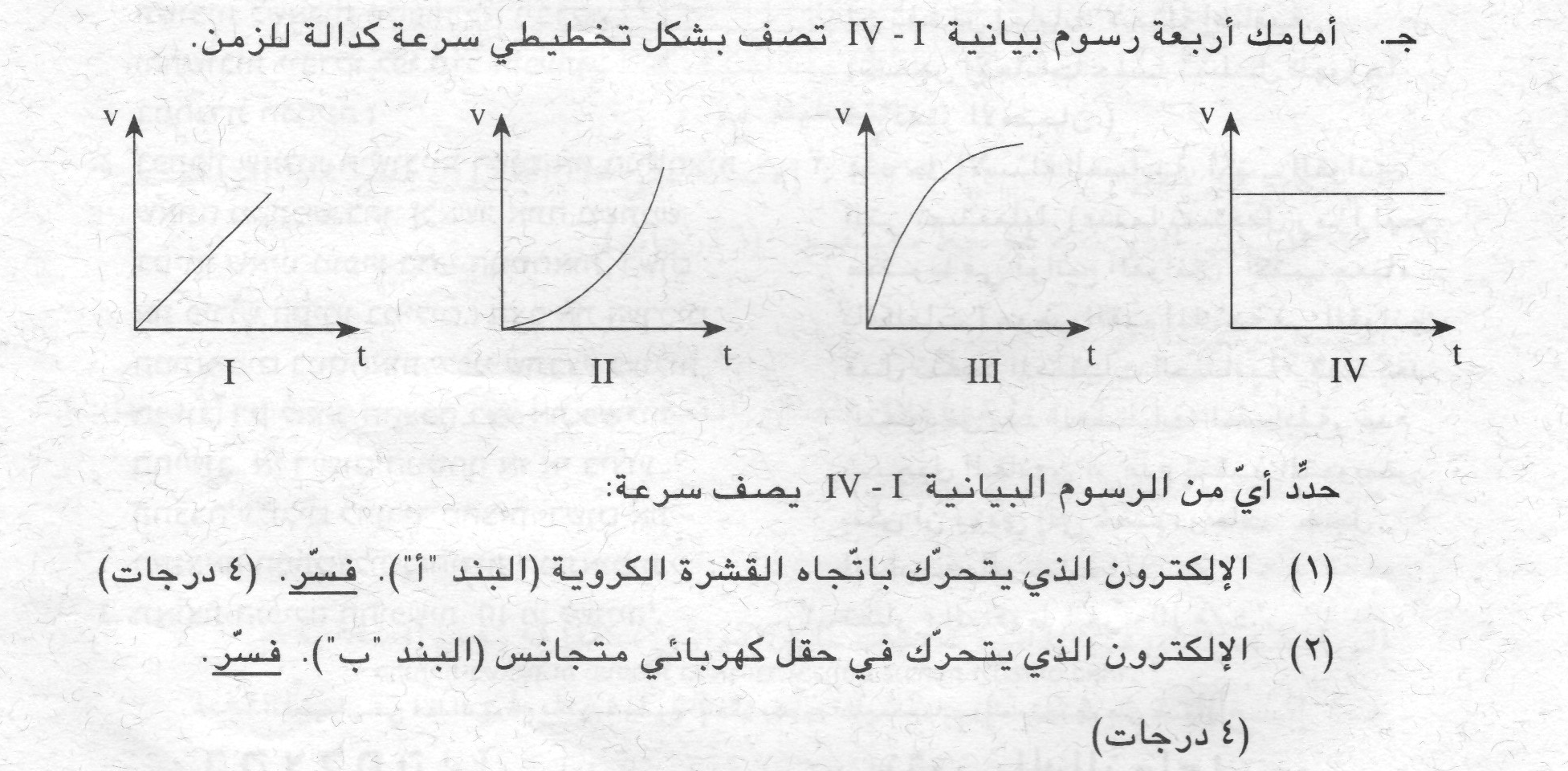
(1) الرسم البياني 2.
(2) الرسم البياني 1.
(2) גרף 1.
ميل الرسم البياني للسرعة بدلالة الزمن، مساويًا للتسارع.
(1) عندما يقترب الإلكترون من الكرة، تزداد القوة الكهربائية المؤثرة عليه، ويتحرك بتسارع متزايد.
ميل الرسم البياني للسرعة كدالة للزمن، مساويًا لتسارع الجسم، والرسم البياني المقابل للحركة ذات التسارع المتزايد هو الرسم البياني 2
لأنه فقط في هذا الرسم البياني يتزايد الميل.
(2) عندما يتحرك الإلكترون في حقل متجانس، تعمل عليه قوة كهربائية ثابتة، من القانون الثاني لنيوتن يتحرك الإلكترون بتسارع ثابت.
الرسم البياني للسرعة كدالة للزمن المقابل للحركة ذات التسارع الثابت هو الرسم البياني 1، لأنه فقط في هذا الرسم البياني يوجد ميل ثابت.
גרף המהירות בתלות בזמן המתאים לתנועה בתאוצה הולכת וגדלה הוא גרף 2, בגרף זה השיפוע הולך וגדל.
(2) כאשר האלקטרון נע בשדה אחיד פועל עליו כוח חשמלי קבוע , האלקטרון נע בתאוצה קבועה.
גרף המהירות בתלות בזמן המתאים לתנועה בתאוצה קבועה הוא גרף 1, בגרף זה השיפוע הוא קבוע.
للإجابة على هذا السؤال يجب فهم كل من الحركتين بمساعدة مبادئ الكهرباء الساكنة والديناميكا ونتذكر من مبادئ الكينماتيكا أنه في الرسم البياني للسرعة كدالة للزمن فإن ميل الرسم البياني يساوي التسارع.
للإجابة على أسئلة البجروت في الكهرباء، يجب عليك أيضًا أن تكون ملّمًا بالميكانيكا.
השליטה בנושאי המכניקה נדרשת גם לשאלות הבגרות בחשמל.
______________________________________________________________________________________