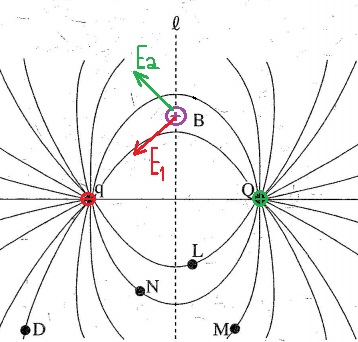
حلول ومنتديات لـ"ألبوم الحلول" في الكهروستاتيكا: 2015,1- شحنة نقطية الحقل الجهد والشغل.

10. 2015,1- شحنة نقطية الحقل الجهد والشغل.

______________________________________________________________________________________

...

الشحنة Q موجبة.

وبمساعدة اتجاه خطوط الحقل يمكن معرفة إشارة الشحنة.

خطوط الحقل تخرج من الشحنة وبالتالي تكون الشحنة موجبة.

1. تتكرر العلاقة بين اتجاه خطوط الحقل وإشارة الشحنة في كثير من الأسئلة.

2. الشحنة هي شحنة نقطية، لذا فهي غير مشار لها تقريبًا.

2. המטען הוא נקודתי , לכן הוא כמעט ולא מסומן.

______________________________________________________________________________________

...

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»Q«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»11«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨»C«/mi»«/math»

استخدام تعبير شدة الحقل الكهربائي حول شحنة نقطية.

نعبر عن مقدار الشحنة Q، من التعبير عن شدة الحقل الناتج عن الشحنة النقطية.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»Q«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»100«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»11«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«mspace linebreak=¨newline¨»«/mspace»«/math»

مقدار الشحنة Q هي : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»11«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«mspace linebreak=¨newline¨»«/mspace»«/math».

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»Q«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»100«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»11«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«mspace linebreak=¨newline¨»«/mspace»«/math»

גודל המטען Q הוא: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»11«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«mspace linebreak=¨newline¨»«/mspace»«/math».

يتم الحصول على وحدة فولط لكل متر من التعبير الملائم لحقل متجانس: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«/mfrac»«/math»

ويتم الحصول على وحدات نيوتن لكل كولون من تعريف الحقل: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mover»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨»q«/mi»«/mfrac»«/math»

وحدة فولط لكل متر تعادل وحدة نيوتن لكل كولون:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#FF0000¨»«mi mathcolor=¨#7F007F¨ mathvariant=¨bold¨»v«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mstyle displaystyle=¨true¨»«mfrac mathcolor=¨#7F007F¨»«mi mathvariant=¨bold¨»J«/mi»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«/mstyle»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»J«/mi»«mrow»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mi mathcolor=¨#007F7F¨ mathvariant=¨bold¨»J«/mi»«mrow»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathcolor=¨#007F7F¨ mathvariant=¨bold¨»N«/mi»«mo mathcolor=¨#007F7F¨ mathvariant=¨bold¨»§#183;«/mo»«menclose mathcolor=¨#007F7F¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«mrow»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«/math»

והיחידות ניוטון לקולון מתקבלות מהגדרת השדה: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mover»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨»q«/mi»«/mfrac»«/math»

היחידות וולט למטר שקולות ליחידות ניוטון לקולון:

______________________________________________________________________________________

...

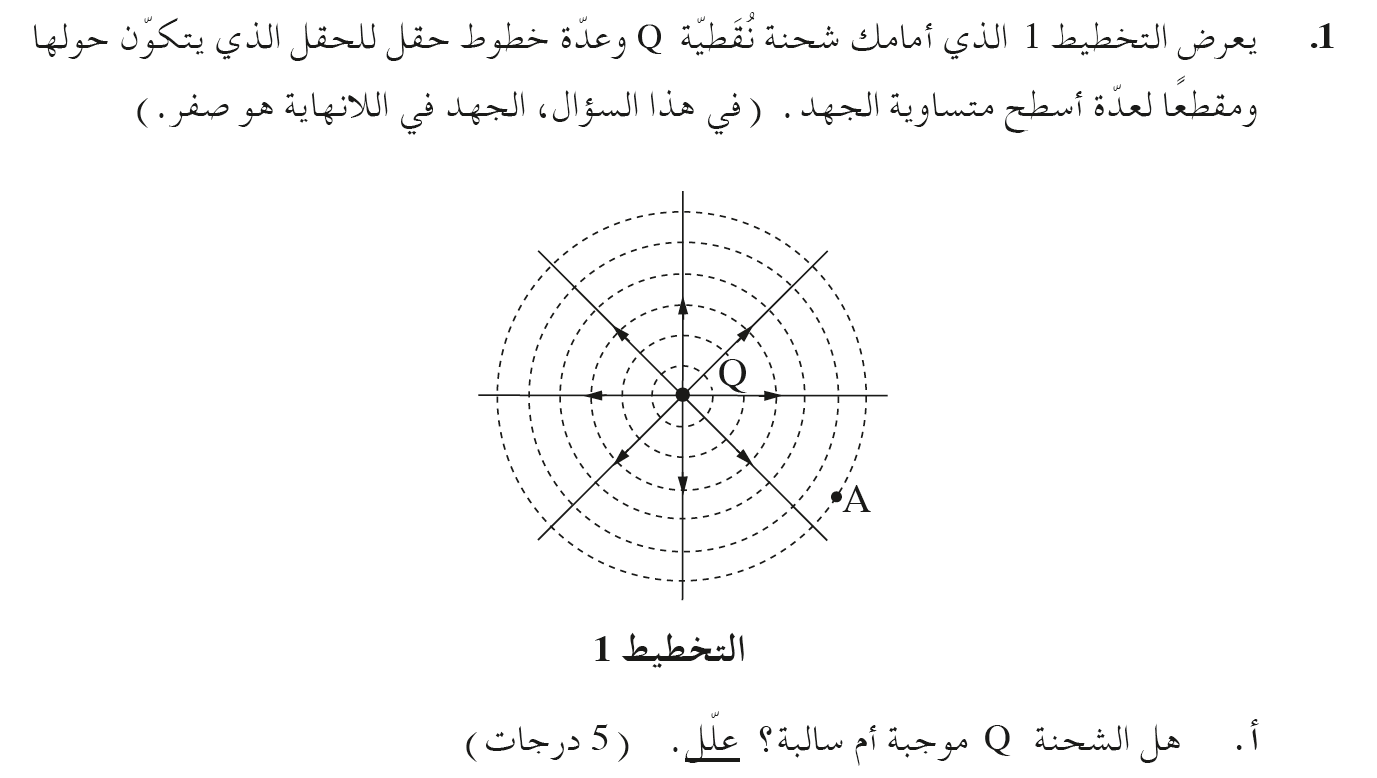
إشارة الشحنة q سالبة. مقدار الشحنة Q تساوي مقدار الشحنة q.

حسب إشارة الشحنة Q والتخطيط يمكن تحديد إشارة الشحنة q ومقدارها.

الشحنة Q موجبة، وخطوط الحقل تخرج منها، ومن التخطيط يمكن أن نرى أن خطوط الحقل تدخل نحو الشحنة q. لأن الشحنة q هي شحنة سالبة.

المخطط متماثل - وبالتالي فإن عدد خطوط الحقل التي تنبثق من الشحنة Q يساوي عدد خطوط الحقل التي تدخل الشحنة q. وبالتالي فإن الشحنتين متساوتان في المقدار.

התרשים סימטרי - לכן מספר קווי השדה היוצאים מהמטען Q , שווה למספר קווי השדה הנכנסים למטען q. לכן המטענים זהים בגודלם.

تتكون عملية الحل من خطوات، وفي كثير من الأحيان يرى الطلاب الخطوات الأولى وليس عملية الحل بأكملها.

لفهم مسار الحل بأكمله، يوصى بإضافة رمز الشحنة Q (+). واتجاه خطوط الحقل الخارجة من الشحنة Q الموجبة.

ثم عندما ترى أن خطوط الحقل تدخل إلى الشحنة q، فإنك تفهم أن الشحنة q سالبة.

عندما لا نُشير إلى أي شيء، فإنك ترى فقط خطوط الحقل بدون اتجاه ولا إشارة للشحنة، ولا تعرف كيف تبدأ.

والفكرة هي - ما يمكن القيام به... ينبغي القيام به، ومن هناك سنستمر. حتى تفهم الحل كاملا.

כדי להבין את מהלך הפתרון בשלמותו , מומלץ להוסיף את סימון המטען Q (+). ואת כיוון קווי השדה היוצאים מהמטען Q החיובי.

ואז כאשר רואים שקווי השדה נכנסים למטען q ,מבינים שהמטען q הוא שלילי.

כשלא מסמנים כלום רק רואים קווי שדה ללא כיוון מטען ללא סימון , לא יודעים איך להתחיל.

הרעיון הוא- מה שאפשר לעשות .... צריך לעשות , ומשם נמשיך. עד להבנת כל הפתרון.

______________________________________________________________________________________

...

لا يساوي صفر.

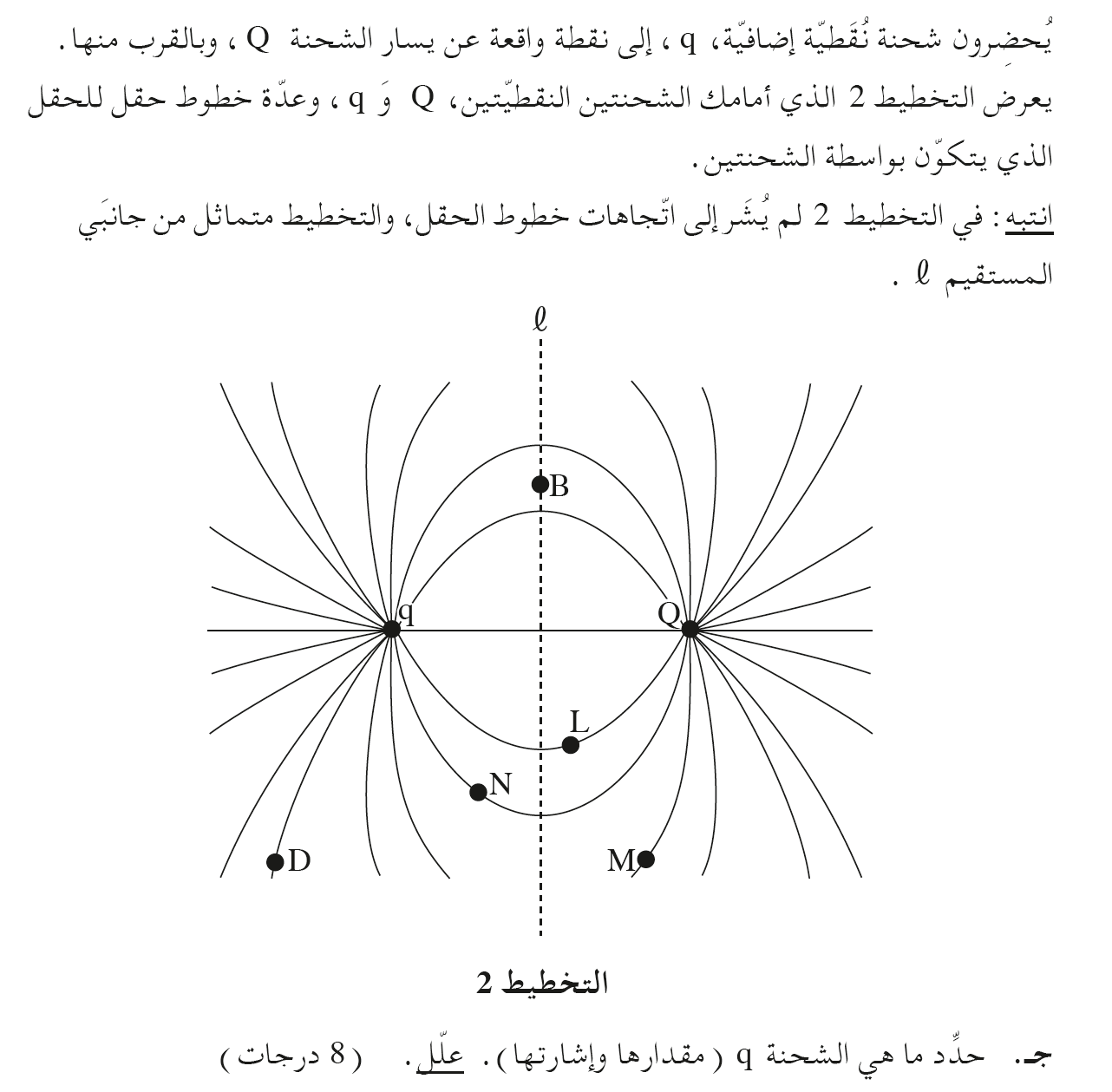
الحقل الكهربائي هو متجه، وشدة الحقل في النقطة B تساوي محصّلة متجهي للحقل اللذان أنشأتهما الشحنتان في هذه النقطة.

في النقطة B يتم إنشاء حقلان من الشحنتين. نرمز إلى الحقل الذي تم إنشاؤه بواسطة الشحنة السالبة q بواسطة E1.

والحقل الذي تم إنشاؤه بواسطة الشحنة الموجبة Q بواسطة E2.

الحقلان الناتجان من الشحنتين في النقطة B لا تُبطل أحدهما الأخرى، وبالتالي فإن محصلة الحقل في النقطة B لا يساوي صفر.

נסמן את את השדה הנוצר מהמטען החיובי Q ב - E2.

השדות שהמטענים יוצרים בנקודה B לא מתקזזים, לכן השדה בנקודה B שונה מאפס.

لا توجد نقطة على مقربة من شحنتين مختلفتين في الإشارة ومتماثلتين في المقدار حيث تكون شدة الحقل صفراً. فكر في الأمر..

______________________________________________________________________________________

د.

______________________________________________________________________________________

...

لا يساوي صفر.

الجهد هو عددي، والجهد في النقطة B يساوي المجموع الحسابي للجهد الناتج من جميع الشحنات في النقطة B.

الجهد هو مقدار عددي. ينتج جهد موجب بالقرب من الشحنة الموجبة. وحول الشحنة السالبة ينتج جهد سالب.

لأن الشحنتين متساويتين في القيمة المطلقة، ولأن النقطة B تقع على نفس البُعد من الشحنتين. الجهد في النقطة B يساوي صفر.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Q«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»Q«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»Q«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»q«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»Q«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»Q«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mstyle mathvariant=¨bold¨»«mrow»«mo»(«/mo»«mo»-«/mo»«mi»Q«/mi»«mo»)«/mo»«/mrow»«/mstyle»«/mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»Q«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/math»

الجهد في النقطة B مساوٍ لصفر.

מכיוון שהמטענים זהים בערכם המוחלט , ומכיוון שהנקודה B נמצאת במרחק זהה מהמטענים . הפוטנציאל בנקודה B שווה לאפס.

הפוטנציאל בנקודה B שווה לאפס.

1. نتعامل مع المقادير الفيزيائية العددية والمتجهة. الفرق بين هذين النوعين من المقادير كبير جدًا، وفي كثير من الأحيان نستخدم المقادير ونميل إلى نسيان طبيعتها المتجهة وهي عددية.

يتناول هذا القسم الفرق بين الحقل وهو متجه، والجهد وهو عددي.

2. مجموعة النقاط التي يكون فيها الجهد صفراً بالقرب من شحنتين متماثلتين في الكمية ومختلفتين في الإشارة، تكون متعامدة مع الخط الواصل بين الشحنتين.

סעיף זה עוסק בהבדל בין השדה שהוא ווקטורי , לבין הפוטנציאל שהוא סקלארי.

______________________________________________________________________________________

...

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»§#1582;§#1575;§#1585;§#1580;§#1610;«/mi»«msub»«mi mathvariant=¨bold¨»W«/mi»«mrow»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«mi mathvariant=¨bold¨»D«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨»J«/mi»«/math»

استخدام تعبير شغل القوة الخارجية.

لا يوجد تغيير في الطاقة الحركية، نصف الشغل باستخدام تعبيرشغل القوة الخارجية:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1582;§#1575;§#1585;§#1580;§#1610;«/mi»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»D«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»N«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»D«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»15«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/math»

من التعبير عن شغل القوة الخارجية، عند بذل شغل لتحريك الشحنة من النقطة N إلى النقطة D،

يكون مقدار الشغل ولكن في إشارته عكسية (سلبة في هذه الحالة):

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1582;§#1575;§#1585;§#1580;§#1610;«/mi»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«mi mathvariant=¨bold¨»D«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»D«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»N«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»15«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/math»

ولذلك، فإن الشغل اللازم لنقل الشحنة من النقطة N إلى النقطة D هو: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1582;§#1575;§#1585;§#1580;§#1610;«/mi»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«mi mathvariant=¨bold¨»D«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»15«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/math»

עבודת הכוח החיצוני שווה בגודלה (והפוכה בסימונה ) לעבודת הכוח החשמלי , לכן גם היא לא תלויה במסלול לאורכו מונע המטען.

1. يمكن لقوة خارجية أن تبذل شغل في تحريك الشحنة بين نقطتين.

التعبير : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#FF0000¨ notation=¨box¨»«mo mathvariant=¨bold¨»§#160;«/mo»«mmultiscripts»«mi mathvariant=¨bold¨»W«/mi»«mrow»«mi mathvariant=¨bold¨»A«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«none/»«mprescripts/»«mrow»«mi mathvariant=¨bold¨»§#1582;§#1575;§#1585;§#1580;§#1610;§#1577;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1602;§#1608;§#1577;«/mi»«/mrow»«none/»«/mmultiscripts»«mo mathvariant=¨bold¨»=«/mo»«mrow»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/menclose»«/math» مناسب فقط إذا لم يكن هناك تغيير في الطاقة الحركية.

2. تعبير شغل القوة الكهربائية: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#FF0000¨ notation=¨box¨»«mi mathvariant=¨bold¨»§#1603;§#1607;§#1585;§#1576;§#1575;§#1574;§#1610;§#1577;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1602;§#1608;§#1577;«/mi»«msub»«mi mathvariant=¨bold¨»W«/mi»«mrow»«mi mathvariant=¨bold¨»A«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mrow»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/menclose»«/math» دائما صحيح . حتى عندما لا تتحرك الشحنة بسرعة ثابتة.

3. هناك أسئلة كثيرة في الكهرباء الساكنة تتناول شغل القوة الخارجية، وعادة ما يتعلق الأمر بشحنة تنتقل من مكان إلى آخر، بحيث لا يحدث تغيير في الطاقة الحركية ومن الممكن استخدام تعبير شغل القوة الخارجية المناسبة للحالة التي لا يحدث فيها تغير في الطاقة الحركية.

______________________________________________________________________________________