______________________________________________________________________________________
...
إشارة الشحنة q موجبة.
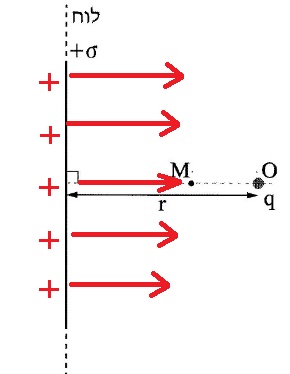
من أجل تكون شدة الحقل في النقطة M، يجب أن تنتج الشحنة النقطية واللوح حقلان متعاكسان في الاتجاه في النقطة M.
يتم شحن اللوح بشحنة موجبة، ويُكوّن في النقطة M حقلًا كهربائيًا موجهًا إلى اليمين.
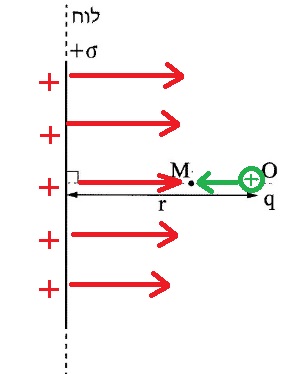
لكي يكون الحقل في النقطة M صفرًا، يجب أن تكون الشحنة النقطية موجبة، بحيث تُكوّن في النقطة M حقلًا كهربائيًا إلى اليسار
لذلك، يجب أن تكون شحنة النقطة في النقطة O موجبة.
כדי שהשדה בנקודה M יתאפס המטען הנקודתי חייב להיות חיובי , כך שבנקודה M הוא ייצר שדה חשמלי שמאלה .
לכן, המטען הנקודתי בנקודה O צריך להיות חיובי.
1. يوصى بالتوصل إلى استنتاجات فقط بعد رسم مخطط عام للشحنة النقطية واللوح والحقلان الكهربائيان لهما في النقطة M.
2. ليست هناك حاجة لايجاد مقدار الشحنة، إنما اشارتها فقط.
2. אין צורך למצוא את גודל של המטען רק את כיוונו.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»§#963;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»K«/mi»«/mrow»«/mfrac»«/math»
من أجل أن تكون محصلة الحقل الكهربائي في النقطة M، يجب أن تُكوِّن الشحنة واللوح حقلان متعاكسان في الاتجاه، ومتساويان في المقدار.
حتى تكون محصلة الحقل الكهربائي في النقطة M صفر، يجب أن تكون شدة الحقل المتجانس والناتج من اللوح المشحون مساوية في المقدار للحقل الناتج من الشحنة النقطيّة في النقطة M.
نشير إلى شدة الحقل الذي كوّنه اللوح بواسطة E1. وشدة الحقل الناتج عن الشحنة النقطيّة في النقطة M بـ E2.
نقوم بمقارنة شدة الحقول والتعبير عن كل من الحقلين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
نُعبّر عن الشحنة q:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»§#963;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»K«/mi»«/mrow»«/mfrac»«/menclose»«/math»
נסמן את גודל השדה הנוצר מהלוח האחיד ב E1 . ואת גודל השדה הנוצר מהמטען הנקודתי בנקודה M ב E2.
נשווה בין עוצמת השדות ונבטא כל אחד משני השדות:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
נבטא את המטען q:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»§#963;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»K«/mi»«/mrow»«/mfrac»«/menclose»«/math»
1. ليس لبعد النقطة M من اللوح أي تأثير على مقدار الشحنة اللازمة. على النقيض من بعد النقطة M من شحنة النقطة.
2. يمكن (لست ملزمًا) عرض تعبير K : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»k«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«/math» , في تعبير الشحنة، ونحصل على تعبير أبسط لمقدار الشحنة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»§#963;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»K«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»§#963;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mstyle displaystyle=¨true¨ mathvariant=¨bold¨»«mfrac»«mn»1«/mn»«mrow»«mn»4«/mn»«mo»§#183;«/mo»«mi»§#960;«/mi»«mo»§#183;«/mo»«msub»«mi»§#949;«/mi»«mn»0«/mn»«/msub»«/mrow»«/mfrac»«/mstyle»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»§#963;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/menclose»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/menclose»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#963;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»d«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#FF0000¨ notation=¨circle¨»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#963;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«/math»
3. عندما يكون هناك حاجة إلى تعبير بدلالة مقادير وثوابت معينة، يجب الوصول إلى تعبير بدلالة هذه المقادير وهذه الثوابت فقط.
2. אפשר להציב את הביטוי של K : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»k«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«/math» , ב
______________________________________________________________________________________

______________________________________________________________________________________
...
البعد s في هذه الحالة مساوٍ لـ d.
من الضروري فحص مدى تأثير الابتعاد عن اللوح المشحون على شدة الحقل الناتج من اللوح في النقطة البعيدة، وبالتالي تحديد مقدار الشحنة q.
شدة الحقل الكهربائي المتجانس الناتج عن اللوح المشحون على بعد S إلى يسار النقطة N هي نفس شدة الحقل الناتج عن اللوح في النقطة M (وأي نقطة أخرى). وبما أن الشحنة النقطية لا تتغير، فإن البعد S يساوي البعد d.
מכיוון שהמטען הנקודתי לא משתנה , המרחק בין הנקודה N לנקודה S שווה למרחק d .
يُنتج اللوح المشحون حقلًا متجانسًا، في الحقل المتجانس، لا تتغير شدة الحقل عندما تبتعد عن اللوح وهذه الحقيقة ليست بديهية.
هذا السؤال وأسئلة أخرى في مجال الكهرباء الساكنة تركز بدقة على هذه الحقيقة غير البديهية.
השאלה הזאת, ושאלות אחרות באלקטרוסטטיקה ממוקדות בדיוק בעובדה לא אינטואיטיבית זאת.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»§#1582;§#1575;§#1585;§#1580;§#1610;«/mi»«msub»«mi mathvariant=¨bold¨»W«/mi»«mrow»«mi mathvariant=¨bold¨»O«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/math»
التعبير عن الشغل بدلالة على فرق الجهد، واستخدام تعبير الحقل المتجانس.
في البداية، كانت الشحنة في النقطة O، وتحركت تحت تأثير قوة خارجية. عند انتهاء تأثير القوة الخارجيةكانت الشحنة في النقطة N.
نجد شغل القوة الخارجية باستخدام تعبير الشغل:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1582;§#1575;§#1585;§#1580;§#1610;«/mi»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨»O«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»N«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold-italic¨»O«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«/math»
نُعبر عن فرق الجهد بدلالة الحقل، من تعبير الحقل المتجانس:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/math»
نُعوض تعبير فرق الجهد في تعبير الشغل:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1582;§#1575;§#1585;§#1580;§#1610;«/mi»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨»O«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«/math»
نُعبر عن شدة الحقل الكهربائي بدلالة كثافة الشحنة، من التعبير عن الحقل الكهربائي الناتج في لوح مشحون:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1582;§#1575;§#1585;§#1580;§#1610;«/mi»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨»O«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«/math»
البعد «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/math» بين النقطة O و N مساوية لـ r. نكتب التعبير النهائي للشغل المطلوب:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1582;§#1575;§#1585;§#1580;§#1610;«/mi»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨»O«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»§#1582;§#1575;§#1585;§#1580;§#1610;«/mi»«msub»«mi mathvariant=¨bold¨»W«/mi»«mrow»«mi mathvariant=¨bold¨»O«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/menclose»«/math»
נמצא את עבודת הכוח החיצוני בעזרת ביטוי העבודה :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1495;§#1497;§#1510;§#1493;§#1504;§#1497;«/mi»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨»O«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»N«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold-italic¨»O«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«/math»
נבטא את הפרש הפוטנציאלים בתלות בשדה , מביטוי השדה האחיד:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/math»
נציב בביטוי העבודה את ביטוי הפרש הפוטנציאלים:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1495;§#1497;§#1510;§#1493;§#1504;§#1497;«/mi»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨»O«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«/math»
נבטא את גודל השדה החשמלי בתלות בצפיפות המטען ,מביטוי השדה החשמלי הנוצר בלוח טעון:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1495;§#1497;§#1510;§#1493;§#1504;§#1497;«/mi»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨»O«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«/math»
המרחק «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/math» בין הנקודה O ל N שווה ל r. נכתוב את הביטוי הסופי לעבודה הדרושה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1495;§#1497;§#1510;§#1493;§#1504;§#1497;«/mi»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨»O«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»§#1495;§#1497;§#1510;§#1493;§#1504;§#1497;«/mi»«msub»«mi mathvariant=¨bold¨»W«/mi»«mrow»«mi mathvariant=¨bold¨»O«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/menclose»«/math»
1. ليست هناك حاجة لقوة خارجية لتحريك شحنة موجبة من النقطة O إلى النقطة N.
لكن لوضع الشحنة في النقطة N في حالة سكون، وليس مجرد مرورها من النقطة، فلا بد من شغل قوة خارجية. .
2. حصلنا على تعبير شغل سالب. وهذا صحيح لأن القوة الخارجية يجب أن تعمل في الاتجاه المعاكس لاتجاه الحركة
وبحسب تعريف الشغل - الشغل سالب.
אך כדי שהמטען ימוקם בנקודה N ללא תזוזה , ולא רק יחלוף על פני הנקודה יש צורך בעבודת כוח חיצוני.
2. קבלנו ביטוי עבודה שלילי. וזה בסדר מכיוון שהכוח החיצוני צריך לפעול בכיוון הנגדי לכיוון התנועה
ובהתאם להגדרת העבודה - העבודה היא שלילית.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mrow/»«mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1582;§#1575;§#1585;§#1580;§#1610;§#1577;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1602;§#1608;§#1577;«/mi»«/mrow»«/msub»«msub»«mi mathvariant=¨bold¨»W«/mi»«mrow»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«mi mathvariant=¨bold¨»P«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«/math»
النقطتان N و P تقعان على نفس السطح المتساوي الجهد.
يمكنك أن تعلم من هذه الحقيقة عن الشغلل اللازم لتحريك الشحنة بين النقطتين.
ניתן ללמוד מעובדה זו על העבודה הדרושה כדי להניע את המטען בין הנקודות.
النقطة P والنقطة N تقعان على نفس السطح المتساوي الجهد، والجهد في هاتين النقطتين هو نفسه
من تعبير الشغل، لا يلزم بذل أي شغل لتحريك الشحنة من النقطة N إلى النقطة P.
מביטוי העבודה, לא נדרשת עבודה כדי להניע את המטען מהנקודה N לנקודה P.
1. إن استخدام الأسطح المتساوية الجهد يساعد في الفهم والتفكير في سبب تساوي الجهد.
2. في الحقل المتجانس، تكون شدة الحقلل ثابتة، لكن الجهد يتغير يصغر في اتجاه خطوط الحقل.
2. בשדה אחיד עוצמת השדה היא קבועה , אך הפוטנציאל משתנה , הוא הולך וקטן במורד השדה.
______________________________________________________________________________________