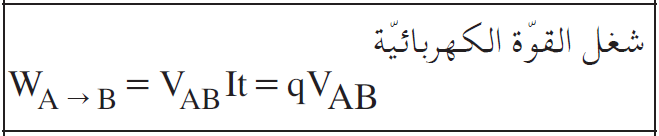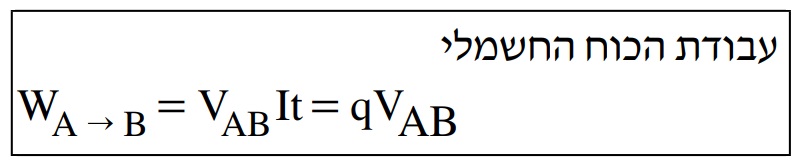______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»10«/mn»«mi mathvariant=¨bold¨»nc«/mi»«/math»
تعبير الجهد حول شحنة نقطية.
نستعمل تعبير الجهد حول شحنة نقطية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»r«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»q«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1000«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»09«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/msup»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»c«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»nc«/mi»«mspace linebreak=¨newline¨»«/mspace»«/math»
شحنة الكرة B1 هي «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»n«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»c«/mi»«/math».
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»r«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»q«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1000«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»09«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/msup»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»c«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»nc«/mi»«mspace linebreak=¨newline¨»«/mspace»«/math»
מטען כדור B1 הוא «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»n«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»c«/mi»«/math».
1. الشحنة السالبة تعمل جهد سالب.
2. مكتوب في السؤال أن الكرة صغيرة الحجم، ولذلك يمكن استخدام عبارة الجهد الموجود بالقرب من شحنة نقطية.
2. מופיע בשאלה שהכדור הוא קטן, לכן ניתן להשתמש בביטוי לפוטנציאל בסביבת מטען נקודתי .
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»S«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»11«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»11«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»3«/mn»«/msup»«mfrac»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«/math»
التعبير عن شدة الحقل الكهربائي بالقرب من شحنة نقطية.
نستخدم التعبير عن شدة الحقل الكهربائي بالقرب من شحنة نقطية.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«/mrow»«msup»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»09«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»90«/mn»«mrow»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»11«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»11«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msup»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«/math»
وبالتالي فإن شدة الحقل الكهربائي هو «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»11«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»11«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msup»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«/mrow»«msup»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»09«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»90«/mn»«mrow»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»11«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»11«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msup»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«/math»
לכן, גודל השדה החשמלי הוא «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»11«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»11«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msup»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«/math»
1. الحقل الكهربائي متّجه، له مقدار واتجاه.
تعبير شدة الحقل الكهربائي «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»Q«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math» هو مقدار عددي، في سياق هذا التعبير، الحقل السالب ليس له معنى، لذلك يجب أخذ القيمة المطلقة للشحنة.
2. التعبير للجهد والحقل بالقرب من شحنة نقطية مُعطاة في مُلحق قوانين البجروت.
3. يبدأ جزء كبير من أسئلة البجروت في مادة الكهرباء الساكنة بمثل هذه البنود البسيطة. البنود الأكثرصعوبةً تكون في آخر السؤال.
ביטוי השדה החשמלי «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»Q«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math» הוא ביטוי סקלארי , בהקשר לביטוי זה אין משמעות לשדה שלילי לכן יש להתייחס לערך המוחלט של המטען.
2. ביטויי הפוטנציאל והשדה בסביבת המטען נקודתי נתונים בדפי הנוסחאות.
3. חלק גדול משאלות הבגרות באלקטרוסטטיקה מתחילות בסעיפים פשוטים כאלו. הסעיפים היותר מאתגרים נמצאים בהמשך.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨»W«/mi»«mrow»«mo mathvariant=¨bold¨»§#8734;«/mo»«mo mathvariant=¨bold¨»§#8594;«/mo»«mi mathvariant=¨bold¨»S«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨»J«/mi»«/math»
استخدام تعبير شغل القوة الخارجية بدلالة فرق الجهد وكمية الشحنة.
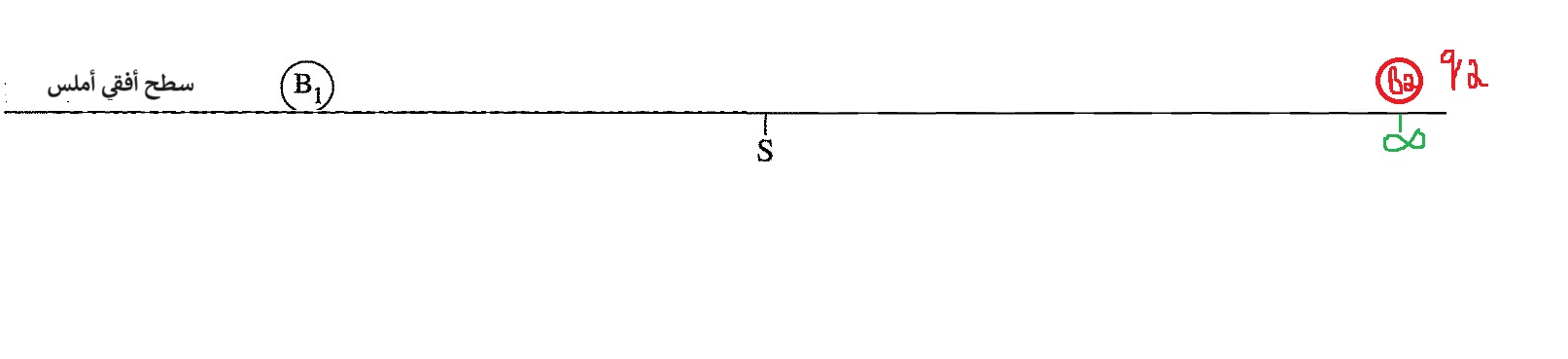
نحسب الشغل الخارجي المطلوب لتحريك الشحنة B2 من نقطة اللّانهاية إلى النقطة S.
معطى أن الشحنة q2 أكبر بمرتين من الشحنة q1 وبالتالي: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»nc«/mi»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1582;§#1575;§#1585;§#1580;§#1610;«/mi»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»§#8734;«/mo»«mo mathvariant=¨bold¨»§#8594;«/mo»«mi mathvariant=¨bold¨»S«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»S«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#8734;«/mo»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1582;§#1575;§#1585;§#1580;§#1610;«/mi»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»§#8734;«/mo»«mo mathvariant=¨bold¨»§#8594;«/mo»«mi mathvariant=¨bold¨»S«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»S«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#8734;«/mo»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1000«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/math»
إن شغل القوة الخارجية المبذول في نقل الشحنة B2 من اللّانهاية إلى النقطة S متساوٍ «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/math» .
נתון שהמטען q2 גדול פי 2 מהמטען q1 לכן :«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»nc«/mi»«/math»

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1495;§#1497;§#1510;§#1493;§#1504;§#1497;«/mi»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»§#8734;«/mo»«mo mathvariant=¨bold¨»§#8594;«/mo»«mi mathvariant=¨bold¨»S«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»S«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#8734;«/mo»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1495;§#1497;§#1510;§#1493;§#1504;§#1497;«/mi»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»§#8734;«/mo»«mo mathvariant=¨bold¨»§#8594;«/mo»«mi mathvariant=¨bold¨»S«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»S«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#8734;«/mo»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1000«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/math»
עבודת הכוח החיצוני המושקעת בהבאת המטען B2 מהאינסוף לנקודה S , שווה «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/math» .
1. يتناول السؤال الحالة التي لا تتغير فيها الطاقة الحركية فيمكن القول أن محصلة القوى تساوي صفراً.
ويتحقق:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1582;§#1575;§#1585;§#1580;§#1610;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1603;§#1607;§#1585;§#1576;§#1575;§#1574;§#1610;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«/math»
2. لا يوجد تعبير لشغلل القوة خارجية في مُلحق القوانين في البجروت. لكن التعبير عن شغل القوة الكهربائية مذكور في صفحات القوانين
(الصيغة ليست في قسم الكهرباء الساكنة، بل هي في موضوع التيار الكهربائي):
ومن هذا التعبير يتبين أن شغل القوة الكهربائية هو: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1603;§#1607;§#1585;§#1576;§#1575;§#1574;§#1610;«/mi»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#FF0000¨»W«/mi»«mrow mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»A«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mrow mathcolor=¨#FF0000¨»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#FF0000¨»q«/mi»«/math»
وبحسب التعبير فإن شغل القوة الخارجية يساوي شغل القوة الكهربائية لكن الإشارة سالبة حسب التعبير التالي: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1582;§#1575;§#1585;§#1580;§#1610;«/mi»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#FF0000¨»W«/mi»«mrow mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»A«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mrow mathcolor=¨#FF0000¨»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#FF0000¨»q«/mi»«/math»
3. من السهل أن نخطئ في إشارة الشغل، فإشارة الشغل تتعلق على عدة أمور:
أ- نوع القوة المنفذة للشغل (قوة كهربائية أو قوة خارجية).
ب- نوع الشحنة التي يتم تنفيذ الشغل عليها.
ج- اتجاه حركة الشحنة أثناء تنفيذ الشغل من الجهد الأعلى إلى الجهد الأقل أو العكس.
4. بالإضافة إلى التعبير عن الشغل بدلالة فرق الجهد، هناك طرق أخرى لإيجاد إشارة الشغل.
أ- إيجاد إشارة الشغل للقوة الخارجية حسب تعريف الشغل: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mrow mathcolor=¨#FF0000¨»«mo mathvariant=¨bold¨»|«/mo»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mrow mathcolor=¨#FF0000¨»«mo mathvariant=¨bold¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«/math».
بما أن القوة الخارجية تعمل في اتجاه الحركة، فإن شغلها يكون موجبًا!
ب. إيجاد إشارة الشغل للقوة الخارجية باستخدام عبارة شغل القوة غير الحافظة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1581;§#1575;§#1601;§#1592;§#1577;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1575;§#1604;§#1594;§#1610;§#1585;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mrow mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1603;§#1604;§#1610;§#1577;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1605;§#1610;§#1603;§#1575;§#1606;§#1610;§#1603;§#1610;§#1577;«/mi»«/mrow»«/msub»«/math»
لا يوجد تغير في الطاقة الحركية، بل تزداد طاقة الوضع وبالتالي تزداد الطاقة الميكانيكية الكلية، ويكون الشغل موجباً!
5. في التمارين يوصى بالتفكير في إشارة الشغل بطرق مختلفة.
2. יש שני סוגים של עבודות באלקטרוסטטיקה, עבודת כוח חשמלי ועבודת כוח חיצוני , אם אין שינוי באנרגיה הקינטית מתקיים:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1495;§#1497;§#1510;§#1493;§#1504;§#1497;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1495;§#1513;§#1502;§#1500;§#1497;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«/math»
כך שהעבודה הכוללת שווה לאפס, וממשפט עבודה אנרגיה אין שינוי באנרגיה הקינטית.
3. ביטוי עבודת הכוח החשמלי נתון בדפי הנוסחאות(לא בחלק האלקטרוסטטיקה, בנושא הזרם החשמלי):
מביטוי זה ניתן לראות שעבודת הכוח החשמלי היא : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1495;§#1513;§#1502;§#1500;§#1497;«/mi»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#FF0000¨»W«/mi»«mrow mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»A«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mrow mathcolor=¨#FF0000¨»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#FF0000¨»q«/mi»«/math»
ובהתאם ביטוי עבודת הכוח החיצוני השווה לה רק הפוכה בסימנה נתונה בביטוי הבא: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1495;§#1497;§#1510;§#1493;§#1504;§#1497;«/mi»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#FF0000¨»W«/mi»«mrow mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»A«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mrow mathcolor=¨#FF0000¨»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#FF0000¨»q«/mi»«/math»
4. בכל מקרה שמבוצעת עבודה כדי להניע מטען בתוך שדה חשמלי (מבלי לשנות את מהירותו) , העבודה שווה להכפלת המטען בהפרש שבין הפוטנציאלים בנקודת תחילת העבודה ונקודת סיום העבודה. ההבדל בין עבודת הכוח החיצוני לעבודת הכוח החשמלי היא רק בסימן העבודה.
5. העבודה היא סקלארית אך היא יכולה להיות שלילית, כמו טמפרטורה.
6. ניתן למצוא את סימן העבודה גם בהתאם להגדרת העבודה :
מהגדרת העבודה «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mrow mathcolor=¨#FF0000¨»«mo mathvariant=¨bold¨»|«/mo»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mrow mathcolor=¨#FF0000¨»«mo mathvariant=¨bold¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«/math» מכיוון שהכוח החיצוני פועל בכיוון התנועה העבודה היא חיובית.
7. עבודת הכוח החיצוני שווה לשינוי באנרגיה המכנית.
7. סימן העבודה המתקבל מהכפלת הפרש הפוטנציאלים במטען חייב להיות זהה לסימן העבודה מהגדרת העבודה, בזמן הבחינה אין צורך לבדוק את סימן המטען בשני דרכים , בתרגול מומלץ לבדוק את סימן המטען.
______________________________________________________________________________________
______________________________________________________________________________________
...
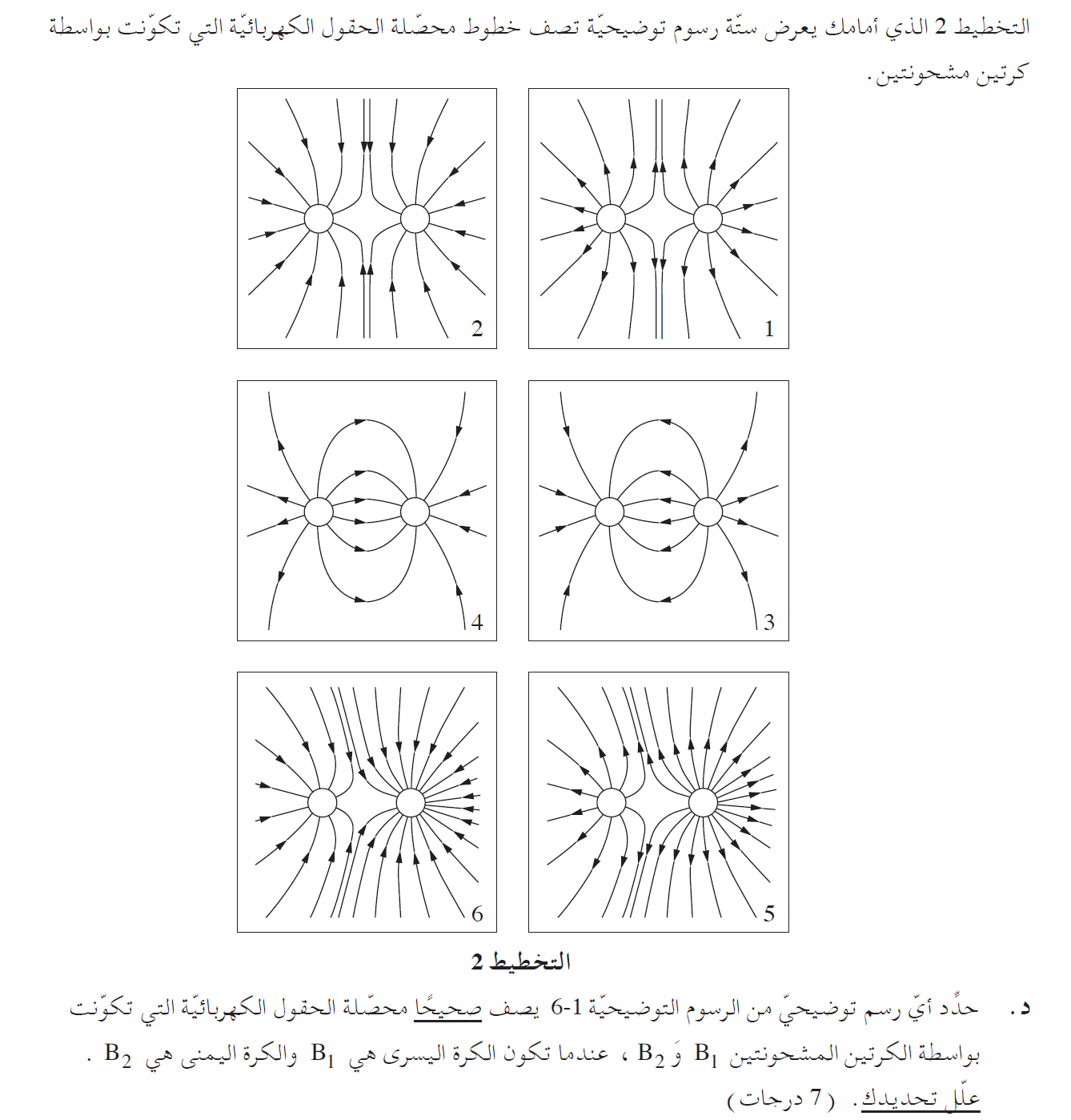
السهم الصحيح هو الرسم 6.
بشكل عام الإلمام بموضوع خطوط الحقل. وفهم العلاقة العامة بين عدد خطوط الحقل والشحنة، والعلاقة بين اتجاه خطوط الحقل ونوع الشحنة.
تكون الشحنات سالبة، لذا يجب أن تدخل خطوط الحقل إلى الشحنة ولا تخرج منها.
بالإضافة إلى ذلك، فإن الشحنة 2 أكبر بمرتين من الشحنة 1، وبالتالي يجب أن تكون كمية خطوط الحقل التي تدخل الشحنة 2 أكبر بمرتين.
ولذلك فإن الشكل الذي يصف الحقل المحصل بشكل صحيح هو الشكل 6..
בנוסף, מטען 2 גדול פי שנים ממטען 1 לכן כמות קווי השדה הנכנסת למטען 2 צריכה להיות גדולה פי שנים.
לכן, האיור המתאר נכונה את השדה השקול הוא איור 6.
في الأسئلة التي تتناول خطوط الحقل، يجب إعطاء أهمية للتفاصيل الصغيرة: اتجاه خطوط الحقل، وعددها، وكثافتها.
______________________________________________________________________________________

______________________________________________________________________________________
...
تعمل الكرتان قوى متساوية.
قوانين نيوتن.
من القانون الثالث لنيوتن - القوة التي تؤثر بها الكرة B1 على الكرة B2 تساوي القوة التي تؤثر بها الكرة B2 على الكرة B1.
לכן הכדורים מפעילים כוחות זהים בגודלם.
السؤال يتناول القوى المؤثرة على الجسم، ولا يتطرق إلى من يؤثر تلك القوى .
ويتناول القانون الثالث القوة التي يؤثر بها الجسم والقوة المؤثرة على الجسم.
لكي تتمكن من حل هذا السؤال، عليك أن تتمكن من القانون الثالث لنيوتن جيدًا. وأكمل الصورة الناقصة التي تظهر في السؤال.
החוק השלישי עוסק בכוח שגוף מפעיל ובכוח המופעל על הגוף.
כדי להצליח לפתור שאלה זו יש להכיר היטב את החוק השלישי של ניוטון. ולהשלים את התמונה הלא מלאה המופיעה בשאלה.
______________________________________________________________________________________

______________________________________________________________________________________
...
سرعة الكرة B1 أكبر من سرعة الكرة B2.
قوانين نيوتن.
يتغير البعد بين الشحنتين، وتتغير القوة المؤثرة عليها، ولكن في أي لحظة تكون القوة المؤثرة على الكرة B2 مساوية في لمقدار القوة المؤثرة على الكرة B1.
كتلة الكرة B2 أكبر بمرتين من كتلة الكرة B1، وفقًا للقانون الثاني لنيوتن، في أي لحظة يكون تسارع الكرة B1 أكبر بمرتين من تسارع الكرة B2.
لذلك، في أي لحظة بعد لحظة تحرير الكرتين، ستكون سرعة الكرة B1 أكبر من سرعة الكرة B2.
מסת כדור B2 גדולה פי שנים ממסת כדור B1 , מהחוק השני של ניוטון בכל רגע תאוצת כדור B1 גדולה פי 2 מתאוצת כדור B2.
לכן, בכל רגע אחרי רגע השחרור מהירות כדור B1 תהיה גדולה ממהירות כדור B2.
كما هو الحال مع البند السابق، هذا البند أيضًا مضلل بعض الشيء. في هذا القسم لا تظهر نصف صورة، بل تظهر صورة ونصف...
سرعة الكرة 1 تكون في أي لحظة أكبر بمرتين من سرعة الكرة 2. ولا علاقة لها بالأماكن التي تتواجد فيها الكرتين.
המהירות של כדור 1 גדולה בכל רגע פי שנים ממהירות כדור 2. ואין כל קשר למקומות בהם נמצאים הכדורים.
______________________________________________________________________________________