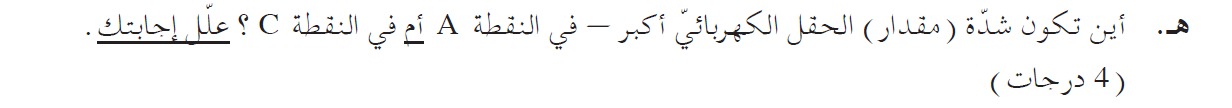
______________________________________________________________________________________
...
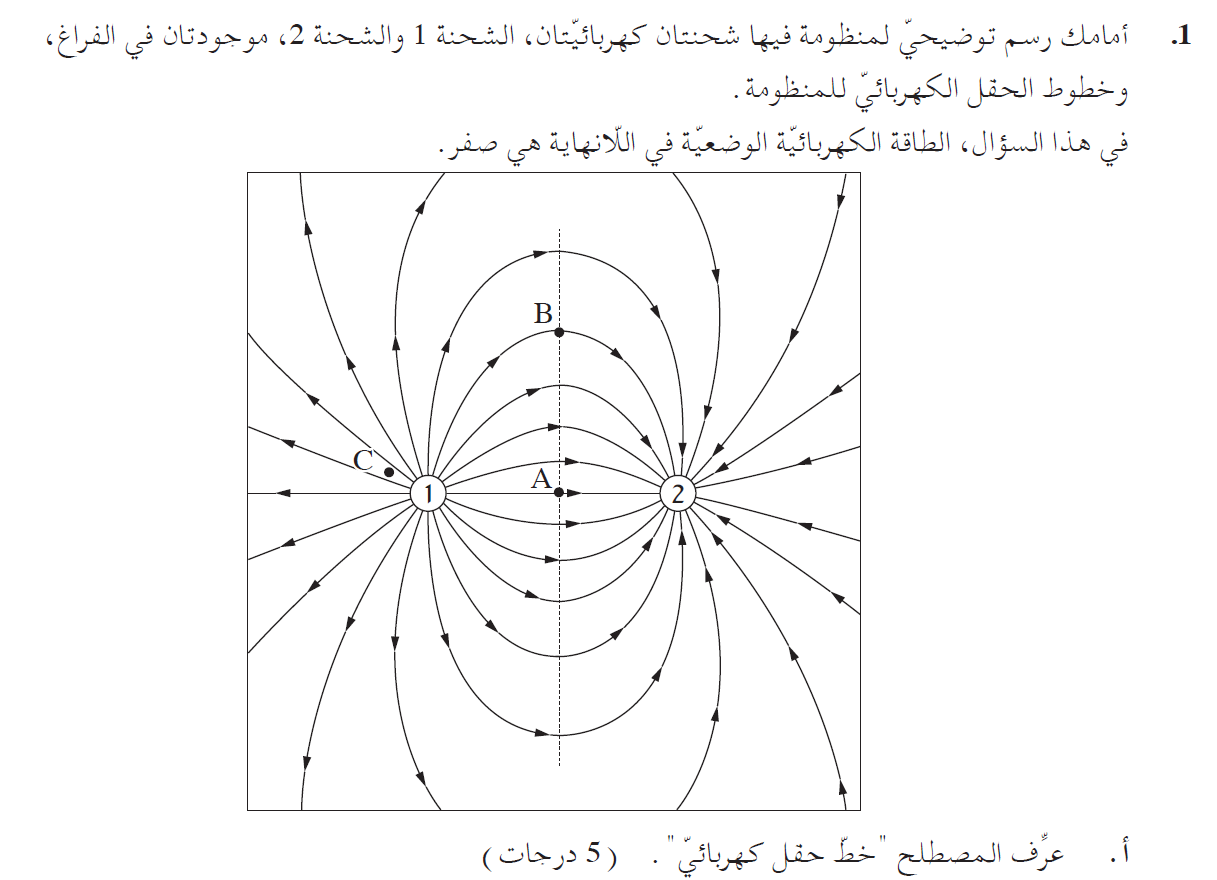
خط الحقل الكهربائي هو خط وهمي اتجاهه في أي نقطة يُمثّل اتجاه الحقل الكهربائي، في أي نقطة على خط الحقل يكون اتجاه الحقل الكهربائي في هذه النقطة مماسا للخط.
فهم معنى خط الحقل الكهربائي.
خط الحقل الكهربائي هو خط وهمي اتجاهه في أي نقطة يُمثّل اتجاه الحقل الكهربائي، في أي نقطة على خط الحقل يكون اتجاه الحقل الكهربائي في هذه النقطة مماسا للخط
1. بشكل عام، يجب الإجابة عن الأسئلة المتعلقة بتعريف المصطلحات بمساعدة التعريف الرسمي
2. كلما اقترب المفهوم من كونه مفهومًا مجردًا مثل الزمن أو الشحنة. من الصعب تحديده.
وفي مثل هذه الحالات، يجب علينا أن نكتب ما نعرفه عن هذا المفهوم.
3. تم تقديم قسم مطابق تمامًا في عام 2016، السؤال 1.
2. ככל שהמושג קרוב יותר להיות מושג מופשט כמו זמן או מטען . יותר קשה להגדיר אותו.
במקרים כאלו יש לכתוב מה שאנחנו יודעים על אותו מושג.
______________________________________________________________________________________
______________________________________________________________________________________
...
عدد خطوط الحقل الخارجة من الشحنة 1 يساوي عدد خطوط الحقل الداخلة نحو الشحنة 2، وبالتالي فإن الشحنات متساوية في القيمة المطلقة.
يتعلق عدد خطوط الحقل التي تدخل أو تخرج من الشحنة على مقدار الشحنة.
يتعلق عدد خطوط الحقل التي تدخل أو تخرج من الشحنة على على مقدار الشحنة.
في الرسم البياني، يخرج 18 خط حقل من الشحنة 1 و- 18 خط حقل يدخل الشحنة 2، وبالتالي فإن الشحنات متساوية في المقدار.
בתרשים יוצאים 18 קווי שדה ממטען 1 ונכנסים 18 קווי שדה למטען 2, לכן המטענים שווים בגודלם.
يتعلق عدد خطوط الحقل الخارجة من الشحنة نوعيًا فقط (وليس كميًا) على مقدار الشحنة.
يصف قانون جاوس العلاقة الكمية بين التدفق الخارج من الشحنة ومقدار الشحنة.
وصف خطوط الحقل هو وصف نوعي ومرئي فقط.
חוק גאוס מתאר באופן כמותי את הקשר שבין השטף היוצא מהמטען לכמות המטען .
תיאור קווי השדה הוא תיאור איכותי וחזותי בלבד.
______________________________________________________________________________________

______________________________________________________________________________________
...
الحقل غير مساوٍ صفر.
استخدام تعريف شدة الحقل الكهربائي في النقطة A.
يتم تعريف شدة الحقل الكهربائي من خلال النسبة بين القوة المؤثرة على شحنة الفحص ومقدار شحنة الفحص.
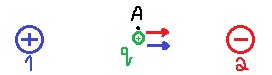
تنبثق خطوط الحقل من الشحنة 1 وبالتالي تكون شحنتها موجبة. تدخل خطوط الحقل في الشحنة 2 وبالتالي فإن الشحنة 2 هي شحنة سالبة.
نرسم مخططًا للقوى المؤثرة على شحنة فحص تقع في النقطة A، بين هاتين الشحنتين.
تعمل القوى الكهربائية التي تؤثر بها الشحنات على شحنة الفحص بطريقة متكاملة.
من تعريف شدة الحقل:«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mover»«mi mathvariant=¨bold¨»§#931;F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨»q«/mi»«/mfrac»«/math» وبما أن محصّلة القوى المؤثرة على شحنة الفحص لا تساوي صفر، فإن الحقل الكهربائي لا يساوي صفر.
קווי השדה יוצאים ממטען 1 לכן מטענו חיובי. קווי השדה נכנסים למטען 2 לכן מטען 2 הוא מטען שלילי.
נערוך תרשים כוחות על מטען בוחן הממוקם בנקודה A, בין שני מטענים אלו.
הכוחות החשמליים שהמטענים מפעילים על מטען הבוחן, פועלים בצורה משלימה .
מהגדרת השדה החשמלי:«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mover»«mi mathvariant=¨bold¨»§#931;F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨»q«/mi»«/mfrac»«/math» מכיוון ששקול הכוחות הפועלים על מטען הבוחן שונה מאפס השדה החשמלי שונה מאפס.
1. الحقل الكهربائي في النقطة A يساوي محصلة متجهات الحقل الناتجة من الشحنات في النقطة A.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#FF0000¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mover»«mi mathvariant=¨bold¨»§#931;F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨»q«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mover»«msub»«mi mathvariant=¨bold¨»F«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨»+«/mo»«mover»«msub»«mi mathvariant=¨bold¨»F«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/mrow»«mi mathvariant=¨bold¨»q«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mover»«msub»«mi mathvariant=¨bold¨»F«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨»q«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«mfrac mathcolor=¨#FF0000¨»«mover»«msub»«mi mathvariant=¨bold¨»F«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨»q«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mover mathcolor=¨#FF0000¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«mover mathcolor=¨#FF0000¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/math»
2. يتم تحديد الحقل الكهربائي عن طريق شحنة الفحص، في أي سؤال حول الحقل الكهربائي في أي نقطة يجب وضع شحنة فحص في النقطة واستخدام تعريف الحقل الكهربائي.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#FF0000¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mover»«mi mathvariant=¨bold¨»§#931;F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨»q«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mover»«msub»«mi mathvariant=¨bold¨»F«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨»+«/mo»«mover»«msub»«mi mathvariant=¨bold¨»F«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/mrow»«mi mathvariant=¨bold¨»q«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mover»«msub»«mi mathvariant=¨bold¨»F«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨»q«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«mfrac mathcolor=¨#FF0000¨»«mover»«msub»«mi mathvariant=¨bold¨»F«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨»q«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mover mathcolor=¨#FF0000¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«mover mathcolor=¨#FF0000¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/math»
2. השדה בחשמלי מוגדר באמצעות מטען בוחן, בכל שאלה של שדה חשמלי בנקודה כלשהי יש למקם בנקודה מטען בוחן
ולהשתמש בהגדרת השדה החשמלי.
______________________________________________________________________________________
ج.

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»V«/mi»«/math»
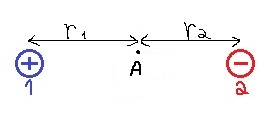
الجهد في النقطة A يساوي مجموع الجهود الناتجة في النقطة بواسطة الشحنتين.
الشحنتان متطابقتان في القيمة المطلقة ومختلفتان في إشارتهما، كما أن بعد كل من الشحنتين من النقطة A متساوٍ. وبالتالي فإن الجهد في النقطة A يساوي صفرًا.
سنكتب تعبيرًا للجهد في النقطة A ونرى أن قيمة التعبير هي صفر:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»Q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»Q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«/math»
الشحنة موجودة في المنتصف تمامًأ، يتحقق: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«/mrow»«/mstyle»«/math». الشحنتان لهما نفس الكمية ولكنهما مختلفتان في الاشارة، ويتحقق: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Q«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Q«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«/math».
نُعوّض في الجهد بالنقطة A:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»Q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»Q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/math»
המטענים זהים בערכם
1. يصف الجهد المحيط حول الشحنة وكذلك الحقل الكهربائي يصف أيضًا المحيط حول الشحنة، لكن الوصفان مختلفان.
هناك حالات يكون فيها الحقل الكهربائي في نقطة ما يساوي صفراً والجهد في هذه النقطة يختلف عن الصفر، وهناك حالات يكون فيها العكس هو الصحيح.
2. ليس من الضروري كتابة تعبير وأن نُبيّن من التعبير أن قيمة الجهد تساوي صفر، يكفي الشرح بإيجاز بالكلمات.
من المهم معرفة كيفية كتابة تعبير وإظهار أن الجهد في نقطة ما يساوي صفرًا.
3. من المهم أن نتذكر الفرق الأساسي بين الحقل والجهد - الحقل هو مقدار متّجه والجهد هو مقدارعددي.
יש מקרים שבהם השדה החשמלי בנקודה שווה לאפס והפוטנציאל בנקודה שונה מאפס , ויש מקרים הפוכים.
2. אין צורך לכתוב ביטוי ולהראות מהביטוי שערך הפוטנציאל שווה לאפס , מספיק להסביר בקצרה באופן מילולי .
חשוב לדעת לכתוב ביטוי ולהראות שהפוטנציאל בנקודה שווה לאפס.
______________________________________________________________________________________

______________________________________________________________________________________
...
سوف تؤثر على الشحنة السالبة قوة إلى اليسار.
احسب اتجاه الحقل وإشارة الشحنة، يمكن تحديد اتجاه الحقل الكهربائي.
وفقًا لوصف خطوط الحقل في الشكل، فإن اتجاه الحقل الكهربائي في النقطة B هو إلى اليمين.
إذا وضعنا شحنة سالبة في النقطة B، فستعمل عليها قوة في الاتجاه المعاكس لاتجاه الحقل، وستكون القوة إلى اليسار.
אם נציב מטען שלילי בנקודה B , יפעל עליו כוח בכיוון ההפוך לכיוון השדה , הכוח יפעל שמאלה.
من تعريف الحقل الكهربائي «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mover»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨»q«/mi»«/mfrac»«/math» اذا كانت الشحنة موجبة اتجاه الحقل الكهربائي في اتجاه القوة الكهربائية .
لكن اذا كانت الشحنة سالبة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mover»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«/math» يتحقق «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mfrac mathcolor=¨#FF0000¨»«mover»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨»q«/mi»«/mfrac»«/math» فإن اتجاه القوة الكهربائية تكون عكس اتجاه الحقل .
אך אם המטען הוא שלילי «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mover»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«/math» מתקיים «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mfrac mathcolor=¨#FF0000¨»«mover»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨»q«/mi»«/mfrac»«/math» כיוון הכוח הפוך לכיוון השדה .
______________________________________________________________________________________
______________________________________________________________________________________
...
شدة الحقل الكهربائي في النقطة C أكبر.
يمكن تقدير شدة الحقل في منطقة معينة اعتماداً على كثافة خطوط الحقل في تلك المنطقة.
يتم تمثيل شدة الحقل الكهربائي في الشكل بواسطة كثافة خطوط الحقل.
في منطقة النقطة C تكون كثافة خطوط الحقل أكبر من كثافة خطوط الحقل في النقطة A.
ولذلك فإن شدة الحقل الكهربائي في النقطة C تكون أكبر أيضًا
באזור הנקודה C צפיפות קווי השדה גדולה יותר מצפיפות קווי השדה בנקודה A, לכן עוצמת השדה החשמלי בנקודה C גם גדולה יותר.
1. كثافة خطوط الحقل تصف بشكل نوعي وعام شدة الحقل الكهربائي. إذا كان مُعطى رسم تخطيطي دقيق لخطوط الحقل، فمن الممكن تقدير شدة الحقل الكهربائي نسبيًا في مجالات مختلفة وفقًا لكثافة خطوط الحقل.
2. شدة الحقل تساوي كميا كثافة التدفق الكهربائي.
3. لا يمكن تقدير شدة الحقل الكهربائي حسب كثافة خطوط الحقل إلا بمخطط دقيق.
لا يمكن رسم مخطط وتقدير شدة الحقل حسب كثافة خطوط الحقل.
2. עוצמת השדה שווה כמותית לצפיפות השטף החשמלי .
3. אפשר להעריך את עוצמת השדה החשמלי בהתאם לצפיפות קווי השדה רק בתרשים מדויק .
לא ניתן לשרבט תרשים ולהעריך את עוצמת השדה בהתאם לצפיפות קווי השדה.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»U«/mi»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨»J«/mi»«/math»
الطاقة الوضعية الكهربائية U للشحنة q، الموجودة في النقطة التي يكون فيها الجهد V معطاة بواسطة: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»q«/mi»«/math».
نجد الجهد الناتج عن الشحنة 1، في المكان الذي تتواجد فيه الشحنة 2:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»Q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»r«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»06«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1500«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/math»
نحسب الطاقة الوضعية الكهربائية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1500«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/math»
لذلك فإنّ الطاقة الوضعية الكهربائية هي: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»Q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»r«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»06«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1500«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/math»
נחשב את האנרגיה הפוטנציאלית :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1500«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/math»
לכן ,האנרגיה הפוטנציאלית של המערכת היא: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/math»
1. يمكن أيضًا حساب الطاقة الوضعية للهيئة عن طريق ضرب الجهد الناتج عن الشحنة 2 في المكان الذي تتواجد فيه الشحنة 1. مضروب بقيمة الشحنة 1.
2. تعبير الطاقة الوضعية الكهربائية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»q«/mi»«/math» والتعبير للجهد الكهربائي حول الشحنة النقطية: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»Q«/mi»«/mrow»«mi mathvariant=¨bold¨»r«/mi»«/mfrac»«/math» موجودان في ملحق قوانين البجروت.
3. من خلال تعويض التعبير للجهد في تعبير الطاقة الوضعية، يمكن الحصول على التعبير عن الطاقة الوضعية لشحنتين نقطيتين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mrow mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»q«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»r«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»q«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»r«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
4. طاقة الوضع سالبة لأن الشحنتين تشكلان "مجموعة مترابطة".
الطاقة الوضعية للأجسام المنجذبة لبعضها البعض تكون سالبة.
בגודל מטען 1.
2. ביטוי האנרגיה הפוטנציאלית «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»q«/mi»«/math» וביטוי הפוטנציאל בסביבת מטען נקודתי: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»Q«/mi»«/mrow»«mi mathvariant=¨bold¨»r«/mi»«/mfrac»«/math» נמצאים בדפי הנוסחאות.
3. מהצבת ביטוי הפוטנציאל בביטוי האנרגיה הפוטנציאלית ניתן לקבל את הביטוי לאנרגיה פוטנציאלית של שני מטענים נקודתיים:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mrow mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»q«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»r«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»q«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»r«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
4. האנרגיה הפוטנציאלית היא שלילית מכיוון שהמטענים מהווים "מערכת קשורה" .
אנרגיה פוטנציאלית של גופים הנמשכים אחד לשני היא שלילית.
______________________________________________________________________________________