**
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»g«/mi»«msub»«mo mathvariant=¨bold¨»*«/mo»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»g«/mi»«msub»«mo mathvariant=¨bold¨»*«/mo»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«/mrow»«/msub»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«/mfrac»«/mstyle»«/math»
التعبير عن تسارع الجاذبية على سطح كل كوكب من معادلة الحركة. التعبير عن نسبة تسارع الجاذبية.
כדי לקבל את יחס התאוצות בתלות בצפיפות ולא בתלות במסה , יש לבטא בעזרת הגדרת הצפיפות את מסת הכוכבים בתלות בצפיפותם .
للتعبير عن تسارع الجاذبية على سطح كل كوكب، نتطرق إلى الجسم المتحرك على سطح الكوكب في السقوط الحر تحت تأثير الجاذبية فقط.
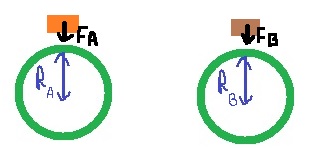
لنقم أولاً برسم مخطط قوى عل الكوكبين:
نكتب معادلة الحركة لكل حالة ، ونعبر عن تسارع الجاذبية من المعادلة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
نعبّر عن نسبة التسارع:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»g«/mi»«msub»«mo mathvariant=¨bold¨»*«/mo»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»g«/mi»«msub»«mo mathvariant=¨bold¨»*«/mo»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mfrac»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mfrac»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
يجب التعبير عن نسبة التسارع بدلالة كثافة الكوكب وليس بدلالة كتلته.
يتم تحديد الكثافة وفقًا للنسبة بين كتلة الكوكب M وحجمه V:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#961;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»V«/mi»«/mfrac»«/math»
نعبر عن حجم الكوكب باستخدام التعبير عن حجم الكرة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»4«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msup»«/math»
نعوّض تعبير الحجم في تعبير الكثافة ونعبر عن كتلة الكوكب منه:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#961;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»V«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»M«/mi»«mrow»«mstyle displaystyle=¨true¨»«mfrac»«mn mathvariant=¨bold¨»4«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/mstyle»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#961;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»4«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msup»«/math»
نستخدم تعبير الكتلة في تعبير نسبة التسارع ، ونعبر عن نسبة التسارع بدلالة كثافة الكوكبين ونصف قطرهما:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»g«/mi»«msub»«mo mathvariant=¨bold¨»*«/mo»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»g«/mi»«msub»«mo mathvariant=¨bold¨»*«/mo»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»M«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»M«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»g«/mi»«msub»«mo mathvariant=¨bold¨»*«/mo»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»g«/mi»«msub»«mo mathvariant=¨bold¨»*«/mo»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#961;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨updiagonalstrike¨»«mstyle displaystyle=¨true¨»«mfrac»«mn mathvariant=¨bold¨»4«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/mstyle»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»§#960;«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«/msub»«menclose notation=¨updiagonalstrike¨ mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»3«/mn»«/menclose»«/msup»«menclose notation=¨downdiagonalstrike¨»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#961;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨updiagonalstrike¨»«mfrac»«mn mathvariant=¨bold¨»4«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»§#960;«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»B«/mi»«/msub»«menclose notation=¨downdiagonalstrike¨ mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»3«/mn»«/menclose»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»g«/mi»«msub»«mo mathvariant=¨bold¨»*«/mo»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»g«/mi»«msub»«mo mathvariant=¨bold¨»*«/mo»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«/mrow»«/msub»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
נערוך תחילה תרשים כוחות , לשני הכוכבים:
נכתוב את משוואת התנועה לכל אחד מהמקרים, ונבטא מהמשוואה את תאוצת הכובד:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
נבטא את יחס התאוצות:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»g«/mi»«msub»«mo mathvariant=¨bold¨»*«/mo»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»g«/mi»«msub»«mo mathvariant=¨bold¨»*«/mo»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mfrac»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mfrac»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
יש לבטא את יחס התאוצות בתלות בצפיפות הכוכב ולא בתלות במסתו.
הצפיפות מוגדרת לפי היחס שבין מסת הכוכב M לנפחו V:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#961;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»V«/mi»«/mfrac»«/math»
נבטא את נפח הכוכב , בעזרת ביטוי נפח כדור :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»4«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msup»«/math»
נציב את ביטוי הנפח בביטוי הצפיפות ונבטא ממנו את מסת הכוכב:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#961;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»V«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»M«/mi»«mrow»«mstyle displaystyle=¨true¨»«mfrac»«mn mathvariant=¨bold¨»4«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/mstyle»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#961;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»4«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msup»«/math»
נשתמש בביטוי המסה בביטוי יחס התאוצות, ונבטא את יחס התאוצות בתלות בצפיפות וברדיוס של הכוכבים:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»g«/mi»«msub»«mo mathvariant=¨bold¨»*«/mo»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»g«/mi»«msub»«mo mathvariant=¨bold¨»*«/mo»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»M«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»M«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»g«/mi»«msub»«mo mathvariant=¨bold¨»*«/mo»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»g«/mi»«msub»«mo mathvariant=¨bold¨»*«/mo»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#961;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨updiagonalstrike¨»«mstyle displaystyle=¨true¨»«mfrac»«mn mathvariant=¨bold¨»4«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/mstyle»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»§#960;«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«/msub»«menclose notation=¨updiagonalstrike¨ mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»3«/mn»«/menclose»«/msup»«menclose notation=¨downdiagonalstrike¨»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#961;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨updiagonalstrike¨»«mfrac»«mn mathvariant=¨bold¨»4«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»§#960;«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»B«/mi»«/msub»«menclose notation=¨downdiagonalstrike¨ mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»3«/mn»«/menclose»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»g«/mi»«msub»«mo mathvariant=¨bold¨»*«/mo»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»g«/mi»«msub»«mo mathvariant=¨bold¨»*«/mo»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«/mrow»«/msub»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
1. تُعرَّف كثافة أي جسم «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#961;«/mi»«/math» بأنها النسبة بين كتلته وحجمه «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#961;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»V«/mi»«/mfrac»«/math». على الرغم من أنه لا نتعامل في كثير من الأحيان
مع الكثافة، إلا أنه مطلوب في المناهج الدراسية.
2. تعريف الكثافة موجود في ملحق القوانين.
3. للكوكب شكل كروي،
للتعبير عن حجم الكوكب من تعبير الكثافة، يجب استخدام الصيغة لحساب حجم الكرة الموجودة في ملحق القوانين.
4. من المهم التعرف على ملحق القوانين جيدًا.
2.לכוכב יש צורה כדורית , בביטוי צפיפות הכוכב נשתמש בנוסחה לחישוב נפח כדור המופיעה בדפי הנוסחאות.
3. חשוב להכיר היטב את דפי הנוסחות. כולל את הביטויים הטריגונומטריים.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mfrac»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mfrac»«/msqrt»«/math»
كتابة معادلة الحركة للحركة الدائرية للقمر الاصطناعي ، والمتحرك في نصف قطر دوران يساوي نصف قطر الكوكب، والتعبير عن زمن الدورة من معادلة الحركة.
في تعبير نسبة زمن الدورة ، نعبّر عن كتلة كل كوكب بدلالة كثافته.
בביטוי יחס זמני המחזור ,נבטא את מסת כל אחד מהכוכבים בתלות בצפיפותו.
نكتب معادلة الحركة الدائرية لكل من الأقمار الاصطناعية ، فالحركة قريبة من سطح النجم، وبالتالي فإن نصف قطر المسار يساوي نصف قطر الكوكب.
نعبّر عن زمن الدورة من المعادلة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mfenced mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«/mfenced»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
نكتب التعبير لزمن الدورة لكل من القمرين الاصطناعيين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
لكي تكون النسبة بين زمني الدورة بدلالة الكثافة وليس بدلالة الكتلة، نعبّر عن الكتل في كل واحد من التعبيرين بدلالة الكثافة.
نستخدم التعبير العام «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#961;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»4«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msup»«/math» من القسم السابق.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«menclose notation=¨horizontalstrike¨»«mn mathvariant=¨bold¨»4«/mn»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«menclose notation=¨downdiagonalstrike¨»«msup»«mrow»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/menclose»«/mrow»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mstyle displaystyle=¨true¨ mathvariant=¨bold¨»«mfrac»«menclose notation=¨horizontalstrike¨»«mn»4«/mn»«/menclose»«mn»3«/mn»«/mfrac»«/mstyle»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»§#960;«/mi»«/menclose»«menclose notation=¨updiagonalstrike¨»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/menclose»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«menclose notation=¨horizontalstrike¨»«mn mathvariant=¨bold¨»4«/mn»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«menclose notation=¨downdiagonalstrike¨»«msup»«mrow»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/menclose»«/mrow»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mstyle displaystyle=¨true¨»«mfrac»«menclose notation=¨horizontalstrike¨»«mn mathvariant=¨bold¨»4«/mn»«/menclose»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/mstyle»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»§#960;«/mi»«/menclose»«menclose notation=¨updiagonalstrike¨»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/menclose»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
نعبّر عن النسبة بين زمني الدورة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mfrac»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mfrac»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mfrac»«/msqrt»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
נבטא מהמשוואה את זמן המחזור:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mfenced mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«/mfenced»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
נכתוב את ביטוי זמן המחזור לכל אחד משני הלוויינים :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
כדי שיחס זמני המחזור יהיו תלוי בצפיפות ולא במסה ,נבטא את המסות בכל אחד משני הביטויים בתלות בצפיפות.
נשתמש בביטוי המסה «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#961;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»4«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msup»«/math» מהסעיף הקודם.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«menclose notation=¨horizontalstrike¨»«mn mathvariant=¨bold¨»4«/mn»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«menclose notation=¨downdiagonalstrike¨»«msup»«mrow»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/menclose»«/mrow»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mstyle displaystyle=¨true¨ mathvariant=¨bold¨»«mfrac»«menclose notation=¨horizontalstrike¨»«mn»4«/mn»«/menclose»«mn»3«/mn»«/mfrac»«/mstyle»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»§#960;«/mi»«/menclose»«menclose notation=¨updiagonalstrike¨»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/menclose»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«menclose notation=¨horizontalstrike¨»«mn mathvariant=¨bold¨»4«/mn»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«menclose notation=¨downdiagonalstrike¨»«msup»«mrow»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/menclose»«/mrow»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mstyle displaystyle=¨true¨»«mfrac»«menclose notation=¨horizontalstrike¨»«mn mathvariant=¨bold¨»4«/mn»«/menclose»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/mstyle»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»§#960;«/mi»«/menclose»«menclose notation=¨updiagonalstrike¨»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/menclose»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
נבטא את יחס זמני המחזור:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mfrac»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mfrac»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mfrac»«/msqrt»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
من التعبير
الذي حصلنا عليه، زمن الدورة T لقمر اصطناعي يتحرك فوق سطح كوكب سيار لا يتعلق
بنصف قطر الكوكب، بل يتعلق فقط بكثافة الكوكب.
ومع ذلك ، فإن
زمن الدورة T
للقمر الاصطناعي الذي يتحرك على ارتفاع h فوق سطح الكوكب لا يتعلّق فقط على كثافة الكوكب،
بل يتعلّق أيضًا على نصف قطر الكوكب وارتفاع القمر الاصطناعي.
אך ,זמן המחזור T של לוויין הנע בגובה h מעל פני הכוכב ,לא תלוי רק בצפיפות הכוכב , הוא תלוי גם ברדיוסו של הכוכב ובגובהו של הלוויין.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»A«/mi»«/msub»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«/math»
تعبير الطاقة الميكانيكية لكل قمر اصطناعي باستخدام صيغة الطاقة الميكانيكية الكلية للقمر الاصطناعي. كتابة النسبة بين الطاقاتين الميكانيكية.
والتعبير عن كتلة كل كوكب بدلالة كثافته.
וביטוי מסת כל כוכב בתלות בצפיפותו.
ביטוי מסות הכוכבים בתלות בצפיפותם.
نستخدم معادلة الطاقة الكلية للقمر الاصطناعي ، ونكتب التعبير للطاقة الكلية لكل من الأقمار الاصطناعية.
نشير إلى كتلة القمر الاصطناعي المتحرك حول الكوكب A بـ mA ، وكتلة القمر الاصطناعي المتحرك حول الكوكب B بـ mB.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«/mfrac»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/math»
نعبّر عن نسبة الطاقات الكلية للقمرين الصناعيين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»A«/mi»«/msub»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨downdiagonalstrike¨»«mo mathvariant=¨bold¨»-«/mo»«/menclose»«mfrac»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«mrow»«menclose notation=¨horizontalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/mrow»«mrow»«menclose notation=¨downdiagonalstrike¨»«mo mathvariant=¨bold¨»-«/mo»«/menclose»«mfrac»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«mrow»«menclose notation=¨horizontalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«/mfrac»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»A«/mi»«/msub»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/math»
نظرًا لأن كتل الأقمار الاصطناعية متساوية ، فيمكننا اختزال كتلتها:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»A«/mi»«/msub»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»A«/mi»«/msub»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»A«/mi»«/msub»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/math»
نعبّر عن كتلة كل من الكوكبين بدلالة كثافتهما ، للحصول على التعبير عن نسبة الطاقة كدالة للكثافة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»A«/mi»«/msub»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»A«/mi»«/msub»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mfrac»«mn mathvariant=¨bold¨»4«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mfrac»«mn mathvariant=¨bold¨»4«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mfrac»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»A«/mi»«/msub»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«/menclose»«/math»
נסמן את מסת הלוויין הנע סביב כוכב A ב mA , ואת מסת הלוויין הנע סביב כוכב B ב mB.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«/mfrac»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/math»
נבטא את יחס האנרגיות הכוללות של שני הלוויינים:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»A«/mi»«/msub»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨downdiagonalstrike¨»«mo mathvariant=¨bold¨»-«/mo»«/menclose»«mfrac»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«mrow»«menclose notation=¨horizontalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/mrow»«mrow»«menclose notation=¨downdiagonalstrike¨»«mo mathvariant=¨bold¨»-«/mo»«/menclose»«mfrac»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«mrow»«menclose notation=¨horizontalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«/mfrac»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»A«/mi»«/msub»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/math»
מכיוון שמסות הלוויינים זהות, נוכל לצמצם את מסתם :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»A«/mi»«/msub»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»A«/mi»«/msub»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»A«/mi»«/msub»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/math»
נבטא את מסות הכוכבים בתלות בצפיפויותיהם , כדי לקבל את ביטוי יחס האנרגיה בתלות בצפיפויות :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»A«/mi»«/msub»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»A«/mi»«/msub»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mfrac»«mn mathvariant=¨bold¨»4«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mfrac»«mn mathvariant=¨bold¨»4«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mfrac»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»A«/mi»«/msub»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«/menclose»«/math»
في
القسمين السابقين، تم اختزال كتلة القمر الاصطناعي في معادلة الحركة، وفي هذا
القسم في تعبير الطاقة لا يتم اختزال كتلة القمر الاصطناعي.
يتم اختزال
الكتلتين في النسبة بين الطاقتين لأنه مُعطى أن الكتلتين متساويتان.
ביחס האנרגיות המסות מצטמצמות מכיוון שנתון שהן זהות.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac»«msub»«mi mathvariant=¨bold¨»V«/mi»«msub»«mi mathvariant=¨bold¨»e«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«msub»«mi mathvariant=¨bold¨»V«/mi»«msub»«mi mathvariant=¨bold¨»e«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mfrac»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨»§#183;«/mo»«mfrac»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«/math»
تطوير تعبير لسرعة الهروب من سطح كل واحد من الكوكبين، والتعبير عن النسبة بين سرعاتي الهروب ، وتعويض كتلة كل كوكب.
أصغر سرعة ابتدائية التي يتم إطلاق الصاروخ بها هي سرعة الهروب من الكوكب.
سرعة الهروب هي السرعة التي تكون عندها الطاقة الميكانيكية الكلية للصاروخ مساوية للصفر.
نقارن الطاقة الميكانيكية الكلية للصاروخ بالصفر ، ونشير إلى سرعة الهروب بالمقدار ve.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»U«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»e«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»e«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»e«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
نكتب تعبير سرعة الهروب لكل كوكب:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»e«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mfrac»«/msqrt»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»e«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«/msqrt»«/math»
نكتب تعبيرًا للنسبة بين سرعتي الهروب:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«msub»«mi mathvariant=¨bold¨»e«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«msub»«mi mathvariant=¨bold¨»V«/mi»«msub»«mi mathvariant=¨bold¨»e«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msqrt»«mfrac»«mrow»«menclose notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mfrac»«/msqrt»«msqrt»«mfrac»«mrow»«menclose notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«/msqrt»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msqrt»«mfrac»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mfrac»«/msqrt»«msqrt»«mfrac»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«/msqrt»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«msub»«mi mathvariant=¨bold¨»e«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«msub»«mi mathvariant=¨bold¨»V«/mi»«msub»«mi mathvariant=¨bold¨»e«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«/math»
للتعبير عن النسبة بين سرعتي الهروب كدالة لكثافة الكوكب ، نعبر عن كتلة الكوكب بدلالة كثافته:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«msub»«mi mathvariant=¨bold¨»e«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«msub»«mi mathvariant=¨bold¨»V«/mi»«msub»«mi mathvariant=¨bold¨»e«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«msub»«mi mathvariant=¨bold¨»e«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«msub»«mi mathvariant=¨bold¨»V«/mi»«msub»«mi mathvariant=¨bold¨»e«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mfrac»«mn mathvariant=¨bold¨»4«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mfrac»«mn mathvariant=¨bold¨»4«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«/menclose»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«msub»«mi mathvariant=¨bold¨»e«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«msub»«mi mathvariant=¨bold¨»V«/mi»«msub»«mi mathvariant=¨bold¨»e«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mfrac»«msub»«mi mathvariant=¨bold¨»V«/mi»«msub»«mi mathvariant=¨bold¨»e«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«msub»«mi mathvariant=¨bold¨»V«/mi»«msub»«mi mathvariant=¨bold¨»e«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mfrac»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨»§#183;«/mo»«mfrac»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«/menclose»«/math»
عندما يتم إطلاق الصاروخ بسرعة الهروب، يتوقف في
اللانهاية.
من اللحظة التي يتم فيها إطلاق الصاروخ، تعمل عليه قوة
الجاذبية فقط، وبالتالي يتحقق حفظ الطاقة الميكانيكية.
عندما يتوقف الصاروخ في اللانهاية، فإن طاقته الحركية مساوية لصفر وكذلك لا يوجد له طاقة وضعية للجاذبية. لذا الطاقة الميكانيكية الكلية للصاروخ عند توقفه تساوي
صفرًا.
نظرًا لتحقق قانون حفظ الطاقة الميكانيكية، حتى عند إطلاق الصاروخ،
فإن طاقته الميكانيكية تساوي صفرًا.
لذلك، إذا تم إطلاق جسم بسرعة الهروب، فإن طاقته
الميكانيكية تساوي صفرًا في كل لحظة، حتى في لحظة الإطلاق.
מרגע שיגור הטיל רק כוח הכובד עושה עבודה על הטיל , לכן האנרגיה המכנית נשמרת.
כאשר הטיל נעצר באין סוף אין לו אנרגיה קינטית ואין לו אנרגיה פוטניאלית כבידתית . האנרגיה המכנית של הטיל שווה לאפס כאשר הוא נעצר.
מכיוון שהאנרגיה המכנית נשמרת ,גם כאשר הטיל שוגר האנרגיה המכנית שלו שווה לאפס.
לכן, אם גוף נזרק במהירות המילוט , האנרגיה המכנית שלו שווה לאפס בכל רגע , גם ברגע השיגור.
______________________________________________________________________________________
 **
**