ألبوم الحلول في الجاذبية

______________________________________________________________________________________

• مجلد
• الجواب النهائي
• إستراتيجية
• الحل الكامل
• انتبهوا

...

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/msqrt»«/math»

يتحقق قانون حفظ الطاقة الميكانيكية، ايجاد التعبير V₀ من حفظ الطاقة الميكانيكية.

يتحرك الصاروخ تحت تأثير الجاذبية فقط ، وبالتالي فإن الجاذبية فقط هي التي تبذل شغل على الصاروخ. يتحقق حفظ الطاقة الميكانيكية الكلية.

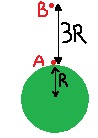
نشير للنقطة التي أُطلق منها الصاروخ بالنقطة A ، والنقطة التي تكون فيها سرعته 0.25Vo بالنقطة B.

نكتب معادلة حفظ الطاقة، بمقارنة الطاقة الميكانيكية الكلية في النقطة A بالطاقة الميكانيكية الكلية في النقطة B:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»

نعوض تعبير السرعة في النقطة A وفي النقطة B:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mfenced mathcolor=¨#0000FF¨»«mrow»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfenced»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»16«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»32«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mfenced mathcolor=¨#0000FF¨»«mrow»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»32«/mn»«/mfrac»«/mrow»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»G«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfenced mathcolor=¨#0000FF¨»«mrow»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«/mrow»«/mfenced»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mfenced mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»15«/mn»«mn mathvariant=¨bold¨»32«/mn»«/mfrac»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»G«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfenced mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»3«/mn»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»G«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfenced mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»32«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»15«/mn»«/mrow»«/mfrac»«/mfenced»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/msqrt»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»

נסמן את הנקודה ממנה שוגר הטיל ב A , ואת הנקודה בה מהירותו 0.25Vo ב B. 

נכתוב את משוואת שימור האנרגיה, נשווה בין האנרגיה המכנית הכוללת בנקודה A , לאנרגיה המכנית הכוללת בנקודה B:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»

נציב את ביטוי המהירויות בנקודה A ובנקודה B:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mfenced mathcolor=¨#0000FF¨»«mrow»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfenced»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»16«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»32«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mfenced mathcolor=¨#0000FF¨»«mrow»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»32«/mn»«/mfrac»«/mrow»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»G«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfenced mathcolor=¨#0000FF¨»«mrow»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«/mrow»«/mfenced»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mfenced mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»15«/mn»«mn mathvariant=¨bold¨»32«/mn»«/mfrac»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»G«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfenced mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»3«/mn»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»G«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfenced mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»32«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»15«/mn»«/mrow»«/mfrac»«/mfenced»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/msqrt»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»

1. في تعبير الطاقة الوضعية، معنى R هو بعد الجسم عن مركز الكوكب، وليس ارتفاع الجسم فوق سطح الكوكب.

 

2. ليس من الممكن أن نفهم مسبقًا كيف يساهم تعبير حفظ الطاقة بالضبط في إيجاد تعبير لـ V₀ ، ولكن يتم حفظ الطاقة وبالتالي يجب كتابة تعبير لحفظ الطاقة.

     بعد كتابة معادلة حفظ الطاقة، سيكون من الممكن فهم أنه يمكن ايجاد V₀ من بعض العمليات الجبرية.

     بشكل عام، في الحالات التي يتم فيها حفظ الحركة أو الطاقة ، يجب كتابة معادلات الحفظ.

 

2. לא ניתן להבין מראש כיצד בדיוק ביטוי שימור האנרגיה תורם למציאת ביטוי ל V0 , אך האנרגיה נשמרת לכן יש לכתוב ביטוי לשימור האנרגיה.

    לאחר כתיבת משוואת שימור האנרגיה , יהיה ניתן להבין שבפעולות אלגבריות ניתן למצוא את V0 .

    באופן כללי , במקרים בהם התנע או האנרגיה נשמרים , יש לכתוב את משוואות השימור. 

______________________________________________________________________________________

______________________________________________________________________________________

• مجلد
• الجواب النهائي
• إستراتيجية
• الحل الكامل
• انتبهوا

...

h=4R

تعبير الارتفاع من معادلة حفظ الطاقة.

يجب أن يكون اتجاه إطلاق الصاروخ لأعلى ، متعامدًا لسطح الأرض ، بحيث تكون الطاقة الحركية في قمة الارتفاع صفراً وتكون طاقة الارتفاع القصوى.

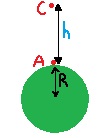
لإيجاد أقصى ارتفاع يمكن أن يصل إليه الصاروخ ، نتطرق إلى إطلاق الصاروخ من سطح الأرض عموديًا إلى أعلى من النقطة A ، ويتوقف في النقطة C.

نرسم رسم تخطيطي ، ونشير بالرسم التخطيطي إلى الارتفاع المطلوب h .

نكتب معادلة حفظ الطاقة:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»h«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»

نعوّض السرعات ونعبر عن الارتفاع h:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»h«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»0«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«mrow»«mi mathvariant=¨bold¨»h«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»h«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mrow»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/mrow»«/mfrac»«/math»

يجب التعبير عن الإجابة بدلالة R فقط ، لذلك نعوّض في V₀ ، التعبير الذي تم الحصول عليه في القسم السابق: 

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mrow»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/menclose»«mrow»«mfrac»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/menclose»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/menclose»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/mrow»«/mfrac»«/math»

نضرب البسط والمقام بـ R:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mrow»«mfrac»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/mfrac»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»R«/mi»«/math»

لذلك توقف الصاروخ على ارتفاع 4 مرات أكبر من نصف قطر الكوكب.

כדי למצוא את הגובה המקסימאלי אליו יגיע הטיל , נתייחס למקרה שהטיל משוגר מפני הקרקע אנכית כלפי מעלה מהנקודה A , ונעצר בנקודה C.

נערוך תרשים, ונסמן בתרשים את הגובה המבוקש h.

נכתוב את משוואת שימור האנרגיה:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»h«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»

נציב את המהירויות , ונבטא את הגובה h:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»h«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»0«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«mrow»«mi mathvariant=¨bold¨»h«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»h«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mrow»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/mrow»«/mfrac»«/math»

יש לבטא את התשובה בתלות ב R בלבד, לכן נציב ב V0 , את הביטוי שהתקבל בסעיף הקודם:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mrow»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/menclose»«mrow»«mfrac»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/menclose»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/menclose»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/mrow»«/mfrac»«/math»

נכפיל את המונה והמכנה של השבר ב R:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mrow»«mfrac»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/mfrac»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»R«/mi»«/math»

לכן, הטיל נעצר בגובה הגדול פי 4 מרדיוס הכוכב.

 1. مطلوب في السؤال التعبير عن الحد الأقصى للارتفاع بدلالة R فقط، ليس من الواضح كيف سيحدث هذا من خلال المعادلات، ولكن بالأخير هذا سيحدث.

     عليك فقط كتابة معادلة حفظ الطاقة ومتابعة العمليات الجبرية حتى تصل إلى الحل.

 

2. طريقة جبرية أبسط من الحل الموضّح هنا: نجد نصف قطر المدار، ثم نطرح نصف قطر الكوكب.

    צריך פשוט לכתוב את משוואת שימור האנרגיה ולהמשיך עם פעולות אלגבריות עד שמגיעים לפתרון.

2. דרך אלגברית יותר פשוטה , מהפתרון המובא כאן: למצוא את רדיוס המסלול , ולהחסיר את רדיוס הכוכב.

______________________________________________________________________________________

______________________________________________________________________________________

• مجلد
• الجواب النهائي
• إستراتيجية
• الحل الكامل
• انتبهوا

______________________________________________________________________________________