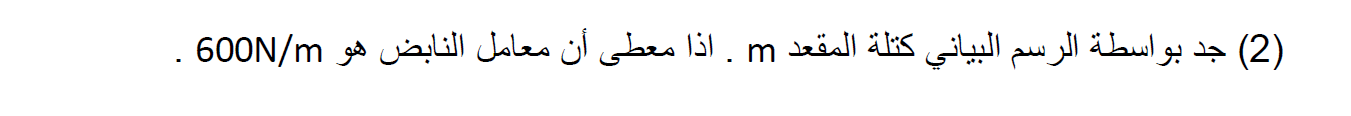
______________________________________________________________________________________
...
72 كغم .
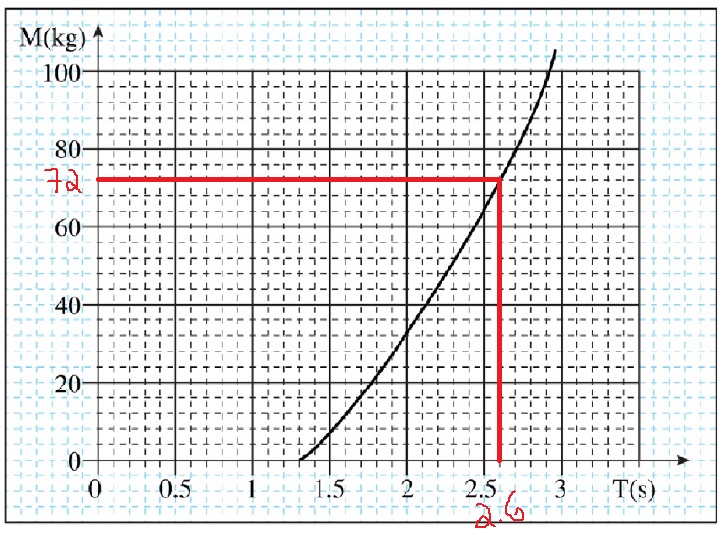
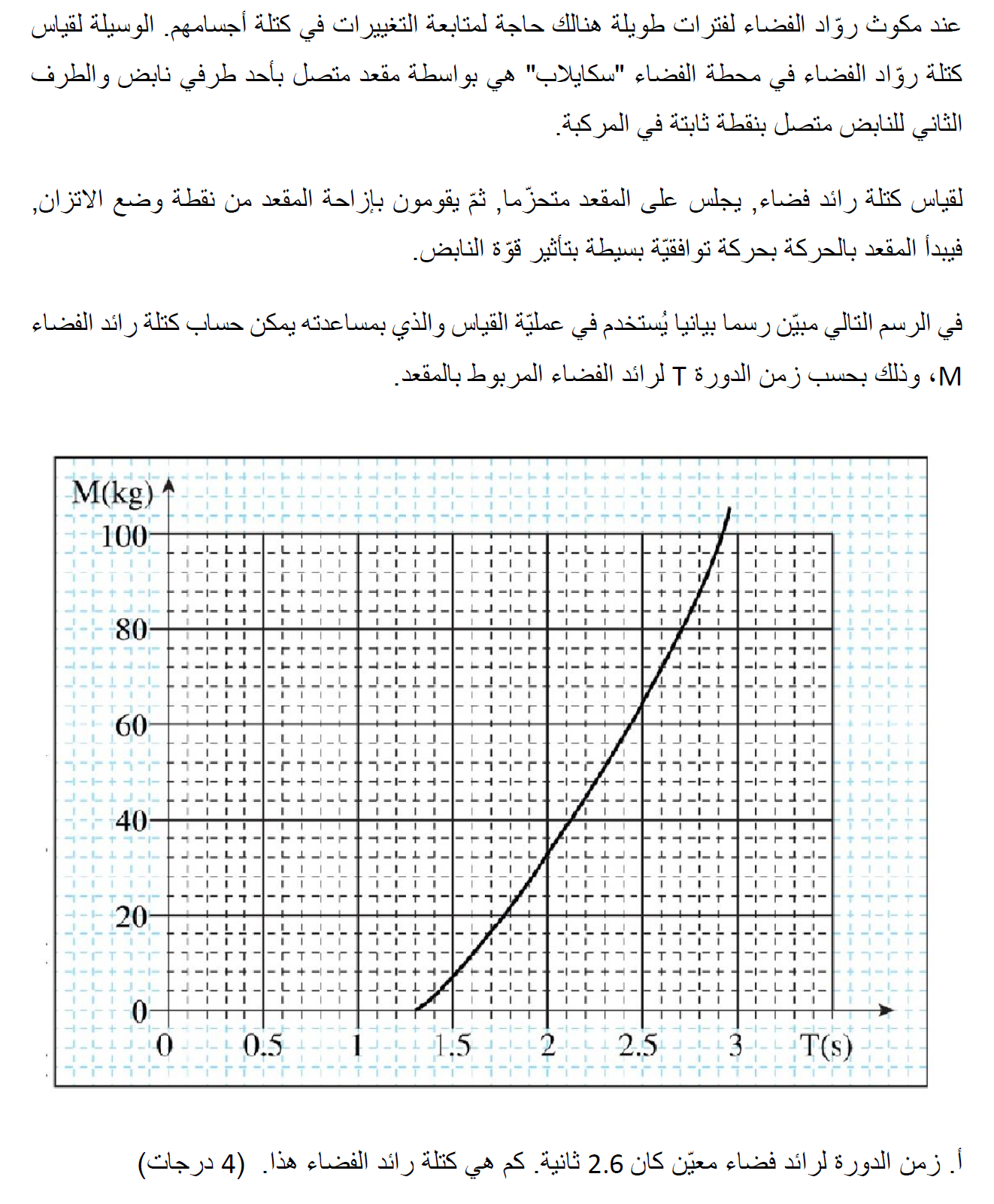
يصف الرسم البياني الكتلة كدالة لزمن دورة الاهتزاز. من الرسم البياني يمكنك إيجاد كتلة رائد الفضاء حسب زمن الدورة.
نجد كتلة رائد الفضاء باستخدام الرسم البياني:
من الرسم البياني يمكن أن نلاحظ أنه خلال دورة زمنية مدتها 2.6 ثانية ، فإن كتلة رائد الفضاء تساوي 72 كغم.
מהגרף ניתן לראות ,שעבור זמן מחזור של 2.6 שניות מסת האסטרונאוט היא 72 ק"ג.
عند الوصول إلى استنتاجات من الوصف البياني، فإن
الاستنتاجات ليست دقيقة دائمًا.
من المهم أن تفهم معنى القيم في المحاور، وأن تشرح أو
تصف كيف توصلت إلى الإجابة.
חשוב להבין את משמעות הערכים בצירים, ולהסביר או לתאר כיצד הגעתם לתשובה.
______________________________________________________________________________________

______________________________________________________________________________________
...
2.6 ثانية.
التعبير لزمن الدورة للحركة توافقية بسيطة لجسم مربوط بنابض.
من تعبير زمن الدورة: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«/mrow»«/mstyle»«/math» , يمكن ملاحظة أن زمن الدورة لا يتعلق بسعة الاهتزاز. يتعلق فقط بكتلة رائد الفضاء وثابت النابض.
1.
ليست هناك حاجة لشرح المنطق القائل بأن زمن الدورة لا يعتمد على سعة الاهتزازات.
يكفي أن نظهر من التعبير لزمن الدورة أنه لا يتعلق بالسعة.
2. المنطق هو أنه
في حالة الاتساع الكبير، يكون المسار الذي يقطعه الجسم في دورة الحركة كبيرًا،
ولكن متوسط سرعة حركة الجسم بين نقاط النهاية كبير أيضًا بحيث لا يتعلق زمن
الدورة على السعة.
2. ההיגיון הוא שבמשרעת גדולה הדרך שעובר הגוף במחזור תנועה גדול , אך המהירות הממוצעת בתנועת הגוף בין נקודות הקצה, גם היא גדולה כך שזמן המחזור לא תלוי במשרעת.
______________________________________________________________________________________

______________________________________________________________________________________
...
T'=1.3S
التعبير لزمن الدورة للحركة توافقية بسيطة لجسم مربوط بنابض.
من تعبير زمن الدورة : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«/mrow»«/mstyle»«/math» يمكن ملاحظة أنه عندما يزيد ثابت النابض 4 مرات، يكون زمن الدورة أصغر بمقدار الجذر التربيعي للرقم 4. لذلك ، يكون زمن الدورة أصغر بمرتين.
لذلك ، إذا زاد ثابت النابض بمقدار 4 مرات ، فإن زمن دورة الاهتزاز سيقل بمقدار مرتين.
לכן, אם קבוע הקפיץ יגדל פי 4 זמן מחזור התנודות יקטן פי 2.
ثابت النابض غير مُعطى، وبالتالي لا يمكن حساب زمن الدورة. ولكن من التعبير عن زمن
الدورة لكل حركة توافقية بسيطة، من الممكن معرفة علاقة زمن الدورة على ثابت
النابض.
من هذه
المعادلة، يمكن فهم أن زمن الدورة أصغر بمرتين، ووجدنا زمن الدورة في الحالة
السابقة، لذلك من الممكن إيجاد زمن الدورة باستخدام ثابت النابض الجديد.
מתלות זו , ניתן להבין שזמן המחזור קטן פי 2 , מצאנו את זמן המחזור במקרה הקודם , לכן אפשר למצוא את זמן המחזור עם קבוע הקפיץ החדש.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«msqrt»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«msqrt»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«/mstyle»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mfenced»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/mfenced»«mspace linebreak=¨newline¨»«/mspace»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mfrac»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«mo mathvariant=¨bold¨»§#160;«/mo»«mspace linebreak=¨newline¨»«/mspace»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mfrac»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»k«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»k«/mi»«/mrow»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«menclose notation=¨circle¨»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»k«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mfenced»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/mfenced»«mspace linebreak=¨newline¨»«/mspace»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mfrac»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«mo mathvariant=¨bold¨»§#160;«/mo»«mspace linebreak=¨newline¨»«/mspace»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mfrac»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»k«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»k«/mi»«/mrow»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«menclose notation=¨circle¨»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»k«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
وصف الكتلة في تعبير زمن الدورة كمجموع كتلة الكرسي وكتلة رائد الفضاء. وحسب ذلك يتم التعبير عن كتلة رائد الفضاء.
نستخدم التعبير عن زمن الدورة لحركة توافقية بسيطة. وسنعبّر عن الكتلة المعطاة في التعبير كمجموع كتلة رائد الفضاء M وكتلة الكرسي m:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«/mstyle»«/math»
نعبّر عن كتلة رائد الفضاء من هذا التعبير:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mfenced mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/mfenced»«mspace linebreak=¨newline¨»«/mspace»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mspace linebreak=¨newline¨»«/mspace»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»k«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»k«/mi»«/mrow»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»k«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«/mstyle»«/math»
נבטא מביטוי זה את מסת האסטרונאוט:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mfenced mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/mfenced»«mspace linebreak=¨newline¨»«/mspace»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mspace linebreak=¨newline¨»«/mspace»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»k«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»k«/mi»«/mrow»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»k«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
الكتلة في تعبير زمن الدورة هي الكتلة التي تتحرك
في حركة توافقية بسيطة، في هذه الحالة من المهم أن نفهم أنه إذا تم ربط كرسي
بنهاية النابض وكان رائد الفضاء جالسًا على الكرسي، فإن الكتلة في التعبير لزمن الدورة
هو مجموع كتلة الكرسي وكتلة رائد الفضاء.
في كثير من الأحيان، يتمثل التحدي من ناحية في فهم
المعنى الدقيق للمقادير الفيزيائية التي تظهر في التعبيرات، ومن ناحية أخرى لفهم
الحالة الموصوفة في السؤال جيدًا بحيث يكون استخدام الصيغة صحيحًا.
הרבה פעמים,האתגר הוא מצד אחד להבין את משמעותם המדויקת של הגדלים הפיזיקליים המופיעים בביטויים , ומצד שני להבין היטב המקרה המתואר בשאלה כך שהשימוש בנוסחה יהיה נכון.
אתגר זה עושה את ההבדל שבין מבחן במתמטיקה, למבחן בפיזיקה.
______________________________________________________________________________________
جـ.
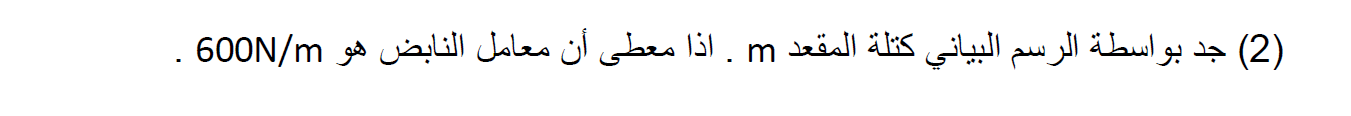
______________________________________________________________________________________
...
m = 30.74kg
وفقًا لكتلة رائد الفضاء من القسم أ. ووفقًا لثابت النابض المعطى في هذا القسم. يمكن التعبير عن كتلة الكرسي من التعبير عن كتلة رائد الفضاء ، القسم ج .1.
لنفترض أن هذا القسم يتعامل مع رائد الفضاء الذي تناوله القسم أ. إذن ، زمن دورة الاهتزازات 2.6 ثانية ، وكتلة رائد الفضاء 74 كغم.
سوف نعبّر عن كتلة الكرسي من كتلة رائد الفضاء ، ونحسب كتلة الكرسي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»k«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»k«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»600«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«msup»«mn mathvariant=¨bold¨»6«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»72«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»102«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»74«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»72«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»74«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»kg«/mi»«/mstyle»«/math»
لذلك ، كتلة الكرسي هي 30.74 كغم.
נבטא את מסת הכיסא ממסת האסטרונאוט , ונחשב את מסת הכיסא:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»k«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»k«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»600«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«msup»«mn mathvariant=¨bold¨»6«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»74«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»102«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»74«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»74«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»28«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»74«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»kg«/mi»«/mstyle»«/math»
1.
كتلة الكرسي وثابت النابض ثابتان. اعتمادًا على كتلة رائد الفضاء، يتم
تحديد زمن الدورة.
يمكن حساب
كتلة الكرسي m
باستخدام T
و M
من أي نقطة في الرسم البياني.
2. هذا السؤال
مضلل، حيث يتم حساب كتلة الكرسي بمساعدة التعبير وليس بمساعدة الرسم البياني فقط.
3. إذا كان الغرض
من التجربة هو إيجاد كتلة الكرسي، فإن التجربة لا تنجح، لأنها تستند إلى نقطة
واحدة في الرسم البياني. من غير المقبول الوصول إلى استنتاج من نقطة واحدة فقط.
4. إذا كان الرسم
البياني يصف كتلة رائد الفضاء اعتمادًا على مربع وقت الدورة، فسيتم الحصول على رسم
بياني خطي، وسيكون من الممكن استخدام الخط المستقيم الأكثر احتمالًا والتعلم منه
بطريقة أكثر نجاحًا ودقة حول كتلة الكرسي.
את מסת הכיסא m ניתן לחשב בעזרת T ו- M .מכל נקודה בגרף.
2. שאלה זו מטעה , שמסת הכיסא מחושב בעזרת הביטוי ולא רק בעזרת הגרף.
3. אם מטרת הניסוי למצוא את מסת הכיסא ,הניסוי לא מוצלח , מכיוון שהוא מתבסס על נקודה אחת בגרף. לא מקובל להגיע למסקנה מנקודה אחת בלבד.
4. אם הגרף היה מתאר את מסת האסטרונאוט בתלות בריבוע זמן המחזור , היה מתקבל גרף ליניארי , ניתן היה להשתמש בישר המסתבר ביותר וללמוד ממנו בצורה יותר מוצלחת ומדויקת על מסת הכיסא.
______________________________________________________________________________________

-
______________________________________________________________________________________
...
يتحرك رائد الفضاء في حركة قمر اصطناعي بنفس حركة القمر الاصطناعي ، لذلك "يطفو" داخل القمر الاصطناعي.
يجب أن يكون مفهوما أن الحركتين متماثلتان ولا تتعلقان ببعضهما البعض.
הלוויין נע בתנועה לוויינית בהשפעת כוח הכבידה שמפעיל כדור הארץ , ובלי כל קשר לתנועה זו , האסטרונאוט נע באותה התנועה בהשפעת כוח הכובד .
يتحرك القمر الاصطناعي تحت تأثير الجاذبية في حركة دائرية ويتحرك رائد الفضاء الموجود بداخله بنفس حركة القمر الاصطناعي ، لذلك إذا وقف رائد الفضاء على مقياس ، فستكون القوة العمودية صفراً ، فإن الوزن الخيالي لرائد الفضاء سيكون صفراً.
1. لا يكفي القول
بأن رائد الفضاء والقمر الاصطناعي يتحركان بنفس السرعة، أو أن رائد الفضاء لا
يتحرك بالنسبة للقمر الاصطناعي.
من المهم أن
نفهم أن كل واحد منهم يتحرك في نفس الحركة الدائرية نتيجة لقوة الجاذبية التي تشغّلها
الأرض عليهم.
2. عندما يكون
الشخص داخل قطار، فإنه يتحرك في نفس حركة القطار. إذا كان يقف على الميزان، فسيظهر
الميزان وزنه الحقيقي، ولن يكون هناك وزن خيالي.
في مثل هذه الحالة، تعتمد حركة الشخص على حركة القطار.
من ناحية أخرى، في حالة وجود رائد فضاء داخل قمر صناعي، فإن حركة رائد الفضاء لا تتعلق
على حركة القمر الاصطناعي، حتى لو "اختفى" القمر الاصطناعي، فسيستمر
رائد الفضاء في التحرك بنفس الحركة تمامًا.
3. من الممكن رسم
مخطّط للقوى المؤثرة على القمر الاصطناعي ورائد الفضاء الموجود على أرضية القمر الاصطناعي،
وكتابة معادلات الحركة للقمر الاصطناعي ورائد الفضاء والتعبير من معادلات الحركة
عن القوة التي تُشغّلها أرضية القمر الاصطناعي على رائد الفضاء ، واثبات أن N يساوي
صفرًا.
4. الوزن الخيالي
لرائد الفضاء هو صفر، لكن وزنه الحقيقي يختلف عن الصفر ويساوي * mg.
כאשר אדם נמצא בתוך רכבת הוא נע בתנועה זהה לתנועת הרכבת. אם יעמוד על מאזניים , המאזניים יציגו את משקלו האמתי, לא יהיה משקל מדומה.
במקרה כזה, תנועת האדם תלויה בתנועת הרכבת . לעומת זאת, במקרה של אסטרונאוט הנמצא בתוך לוויין תנועת האסטרונאוט לא תלויה בתנועת הלוויין , גם אם הלוויין "יעלם" האסטרונאוט ימשיך לנוע בדיוק באותה התנועה .
אפשר לערוך תרשים כוחות ללוויין ולאסטרונאוט הממוקם על רצפת הלוויין , לכתוב את משוואות התנועה ללוויין ולאסטרונאוט ולבטא ממשוואות התנועה את הכוח שרצפת הלוויין מפעילה על האסטרונאוט , ולראות ש N שווה אפס.
______________________________________________________________________________________
______________________________________________________________________________________