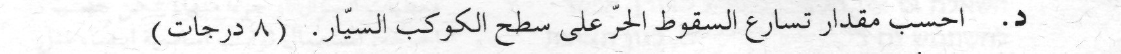
______________________________________________________________________________________
...
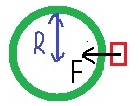
الرسم أ.
القانون الأول لنيوتن، قانون الجاذبية العام.
حتى يكون رائد الفضاء في حالة سكون بالنسبة لمركز الكوكب. يجب ألا تتحرك السفينة الفضائية بالنسبة إلى الكوكب. من القانون الأول لنيوتن ، يجب أن تكون محصّلة القوى على السفينة الفضائية صفرًا.
تجذب الجاذبية السفينة الفضائية في اتجاه المركز للداخل ، بحيث تكون محصّلة القوى عليها صفرًا ، يجب أن يشغّل محرك سفينة الفضاء قوة على السفينة الفضائية في اتجاه طارد عن المركز .
لذلك ، فإن الرسم البياني الصحيح هو الرسم البياني أ.
כוח המשיכה מושך את החללית בכיוון רדיאלי פנימה ,כדי ששקול הכוחות יהיה אפס, מנוע החללית צריך להפעיל על החללית כוח רדיאלי החוצה.
לכן,התרשים הנכון הוא תרשים א'.
إذا تحركت السفينة الفضائية في حركة قمر اصطناعي، كما في
الرسم التخطيطي "د". لن يتغير البعد بين مركز الكوكب والسفينة الفضائية،
ولكن سيتغير موقع مركز الكوكب بالنسبة للسفينة الفضائية.
في مثل هذه الحالة، في لحظة ما ستكون نقطة مركز الكوكب
فوق السفينة الفضائية، وفي لحظة أخرى أسفل السفينة الفضائية.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»=«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»7«/mn»«/msup»«mi mathvariant=¨bold¨»m«/mi»«/math»
هندسة.
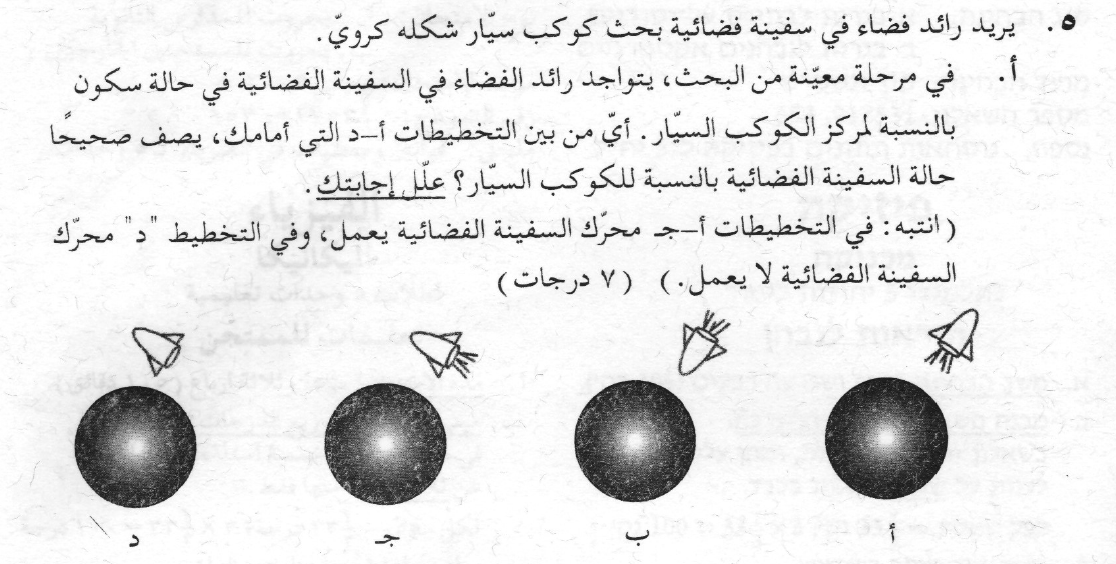
نجد نصف قطر الكوكب R هندسيًا. نتطرق إلى المثلث OBC التالي:
طول الضلع OB هو نصف قطر الكوكب. الضلع BC هو خط يمُّس سطح الكوكب. لذلك فهو عمودي على نصف قطر الكوكب في نقطة التماس.
المثلث OBC هو مثلث قائم الزاوية. الزاوية BCO تساوي 30 درجة ، ومعطى الارتفاع H ، لإيجاد طول نصف القطر ، سنستخدم نسبة الجيب (sin):
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»OB«/mi»«mi mathvariant=¨bold¨»OC«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»H«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mfenced mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»H«/mi»«/mrow»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»H«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»H«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»H«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»H«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»H«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»30«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»30«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»7«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»30«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»30«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»7«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨»7«/mn»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
لذلك فإن نصف قطر الكوكب هو عشرة ملايين متر.
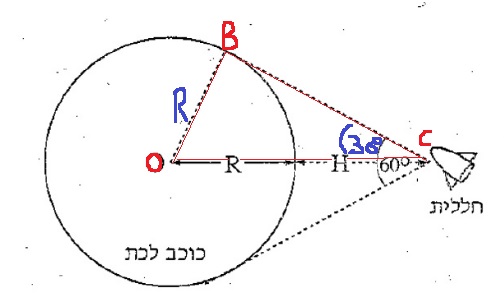
אורך הצלע OB הוא רדיוס הכוכב. נתייחס לצלע BC כאל ישר המשיק לפני הכוכב. לכן הוא ניצב לרדיוס הכוכב בנקודת ההשקה.
המשולש OBC הוא משולש ישר זווית. הזווית BCO שווה ל 30 מעלות, ונתון גובה H , כדי למצוא את אורך הרדיוס , נשתמש בזהות הסינוס:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»OB«/mi»«mi mathvariant=¨bold¨»OC«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»H«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»H«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»H«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»H«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»H«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»7«/mn»«/msup»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»30«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»7«/mn»«/msup»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨»7«/mn»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
לכן רדיוס הכוכב הוא עשרים מליון מטר.
1. في الهندسة، لا ترى دائمًا مسار الحل المطلوب، امنح
نفسك بعض الوقت. في بعض الأحيان، تكون لحظات قليلة من التفكير والتمعن كافية
للوصول إلى الطريق الأمثل.
2. الامتحان يدور حول المبادئ الفيزيائية وليس الهندسة،
وبالتالي فإن العمليات الهندسية عادة ما تكون بسيطة للغاية.
3. إذا لم تجد نصف قطر المسار، لأنك تحتاج إلى قيمته لاحقًا
في السؤال، فاكتب ببساطة أنك لم تجد قيمته، وللمتابعة، حدد أن نصف قطره هو ....
دعنا نقول كنصف قطر الكرة الأرضية (أو القمر، أو أي نصف قطر معقول لنجم من
اختيارك). بهذه الطريقة تخسر النتيجة في قسم واحد فقط وليس السؤال بأكمله.
4. ظهر هذا القسم والأقسام التالية في امتحان البجروت لعام
1997 ، واحتوى الرسم التخطيطي هناك على زاوية قائمة. على عكس التخطيط هنا.
2. אתם נבחנים על העקרונות הפיזיקליים ולא על גיאומטריה , לכן הפעולות הגיאומטריות לרוב הן די פשוטות.
3. במידה ולא מצאתם את רדיוס המסלול ,מכיוון שאתם זקוקים לערכו בהמשך השאלה, פשוט תכתבו שלא מצאתם את ערכו , וכדי להמשיך אתם קובעים שרדיוסו הוא.... נניח כרדיוס כדור הארץ(או הירח, או כל רדיוס סביר של כוכב שתבחרו ) . כך אתם מפסידים רק את הניקוד על סעיף אחד ולא את כל השאלה.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»84«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»25«/mn»«/msup»«mi mathvariant=¨bold¨»Kg«/mi»«/math»
معادلة الحركة للحركة الدائرية ، والتعبير عن كتلة الكوكب من معادلة الحركة.
نرسم مخطّط للقوى المؤثرة على سفينة الفضاء:
القوة الوحيدة المؤثرة على السفينة الفضائية هي قوة الجاذبية التي يشغّلها الكوكب على السفينة الفضائية.
نشير إلى نصف قطر مدار السفينة الفضائية بواسطة R ، ونصف قطر الكوكب بواسطة 'R.
نكتب معادلة الحركة الدائرية. ونعبّر عن كتلة الكوكب من المعادلة.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mfenced mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»G«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»`«/mo»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»H«/mi»«msup»«mo mathvariant=¨bold¨»)«/mo»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»G«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»(«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»7«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»7«/mn»«/msup»«msup»«mo mathvariant=¨bold¨»)«/mo»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«mrow»«msup»«mfenced»«mrow»«mn mathvariant=¨bold¨»150«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»60«/mn»«/mrow»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»11«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»23«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»84«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨»25«/mn»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»kg«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»

הכוח היחיד הפועל על החללית הוא כוח הכבידה שהכוכב מפעיל על החללית. נכתוב את משוואת התנועה של המעגלית.
ונבטא מהמשוואה את מסת הכוכב.
נסמן את רדיוס מסלול תנועת החללית ב R , ואת רדיוס הכוכב ב 'R.
1. زمن الدورة معطى بوحدات غيراساسية. يجب تعيين قيمة زمن
الدورة بوحدات الثواني.
2. من السهل ارتكاب خطأ في الحسابات في فصل الجاذبية، في
هذا الفصل من المهم بشكل خاص تقييم احتمالية النتيجة التي تم الحصول عليها. قيمة
الكتلة التي حصلنا عليها أقل من كتلة الشمس ولكنها أكبر من كتلة الأرض. لذلك، يمكن
أن تتوافق القيمة التي حصلنا عليها مع قيمة كتلة كوكب ما.
______________________________________________________________________________________
______________________________________________________________________________________
...
مقدار تسارع الجاذبية 38.9 مترًا لكل ثانية مربعة.
رسم مخطّط القوى المؤثرة ومعادلة القوى، والتعبير عن تسارع الجاذبية من معادلة القوى.
لإيجاد تسارع الجاذبية على سطح الكوكب، نأخذ جسم يتحرك في حالة سقوط حر على سطح الكوكب.
القوة الوحيدة المؤثرة على الجسم هي قوة الجاذبية ، لنرسم مخطّط القوى المؤثرة على الجسم:
نكتب معادلة الحركة ، ونعبر منها عن تسارع الجاذبية على سطح الكوكب:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨»*«/mo»«/msup»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»11«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»84«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»25«/mn»«/msup»«/mrow»«msup»«mfenced»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»7«/mn»«/msup»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»89«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»15«/mn»«/msup»«/mrow»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»14«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»38«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
لذلك ، فإن تسارع الجاذبية على سطح الكوكب تساوي 38.9 مترًا لكل ثانية مربعة.
הכוח היחיד הפועל על הגוף הוא כוח הכובד, נערוך תרשים כוחות :
נכתוב את משוואת התנועה:
1. حصلنا على تسارع جاذبية أكبر بـ 4 مرات من تسارع
الجاذبية على سطح الأرض. وهذا معقول، لأن الكتلة أكبر بحوالي 10 مرات ونصف القطر
أكبر بقليل، كثافة النجم أكبر من كثافة الأرض، وبالتالي فإن تسارع الجاذبية على
سطح الكوكب أكبر.
2. يتم تحديد تسارع الجاذبية على سطح الأرض فقط بواسطة g، وفي كل مكان آخر يتم تمييز تسارع الجاذبية بإشارة *g.
3. مقدار تسارع السقوط الحر، وبعبارة أخرى، تسارع الجاذبية،
وبعبارة أخرى ... شدة حقل الجاذبية على سطح الكوكب.
2. רק תאוצת הכובד על פני כדור הארץ מסומנת ע"י g , בכל מקום אחר מסומנת תאוצת הכובד ב *g.
3. גודל תאוצת הנפילה החופשית , זה במילים אחרות תאוצת הכובד, ובמילים אחרות..שדה הכבידה על פני כוכב הלכת.
______________________________________________________________________________________

______________________________________________________________________________________
...
أثناء الحركة الدائرية ، لا يلزم تشغيل محركات السفينة الفضائية.
معرفة مبادئ حركة القمر الاصطناعي.
تتحرك السفينة الفضائية في حركة القمر الاصطناعي ، في كل حركة قمر اصطناعي، تكون قوة الجاذبية هي قوة الجاذبة نحو المركز، ولا توجد حاجة إلى قوة إضافية للسفينة الفضائية للتحرك في حركة القمر الاصطناعي.
هكذا يتحرك القمر حول الكرة الأرضية والأرض حول الشمس وجميع الكواكب في حركة دائرية بدون محركات.
כך גם נע הירח סביב כדור הארץ ,וכדור הארץ סביב השמש , וכל כוכבי הלכת , בתנועה מעגלית ללא מנועים.
1. كما هو الحال في السقوط الحر، ليست هناك حاجة لمحرك
لتحريك الأجسام الساقطة إلى أسفل، ومن الواضح أنها تسقط بسبب الجاذبية فقط. تمامًا
كما هو الحال في حركة القمر الاصطناعي، تتحرك الأجسام في حركة دائرية نتيجة
للجاذبية وحدها.
2. يرى الطلاب غالبًا سؤالًا بسيطًا، ولا يكلفون أنفسهم
عناء كتابة تعليل لأنه بسيط ومعروف. ولكن حتى أبسط الأسئلة يجب أن يكون لها تعليل
جيد.
2. לעתים קרובות תלמידים רואים שאלה פשוטה,ולא מתאמצים לכתוב נימוק כי זה פשוט, וידוע . אך גם השאלות הפשוטות ביותר צריכות להיות מנומקות היטב.
______________________________________________________________________________________
______________________________________________________________________________________