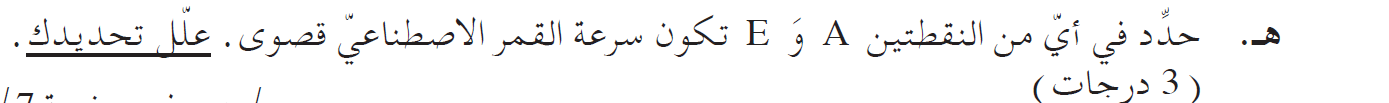______________________________________________________________________________________
...
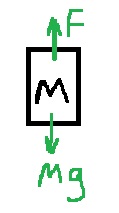
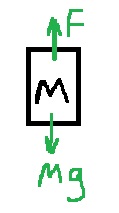
مخطّط القوى المؤثرة على الصاروخ:
من الضروري فهم القوى المؤثرة على الصاروخ واتجاه كل قوة.
تؤثر قوتان على الصاروخ ، قوة الجاذبية نحو الأسفل، والقوة التي يشغّها المحرك على الصاروخ نحو الأعلى.
يدور السؤال أثناء عملية الإطلاق، عندما تعمل القوة F، يجب افتراض أن السطح في هذا الوقت لا يشغّل قوة عمودية على
الصاروخ.
______________________________________________________________________________________

______________________________________________________________________________________
...
أقصى تسارع هو 5.89 مترًا لكل ثانية مربعة. واتجاهه لأعلى.
القانون الثاني لنيوتن ، مع أقصى قوة.
أقصى مقدار للتسارع عندما تكون القوة F قصوى. نجد التسارع الأقصى باستخدام القانون الثاني لنيوتن :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#931;F«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»16«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»7«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»5«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»7«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»5«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»89«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
إذن ، مقدار التسارع 5.89 مترًا لكل ثانية مربعة. اتجاه التسارع باتجاه القوة المحصّلة لأعلى.
يتعلق التسارع على القوة المحصّلة وليس فقط على قوة المحرك،
هذا واضح عندما تتذكر هذا الشيء فمن السهل نسيانه.
______________________________________________________________________________________

______________________________________________________________________________________
...
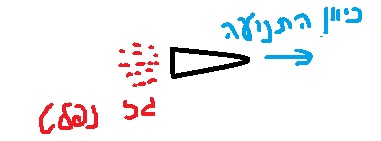
المحرك الصاروخي هو محرك يُطلق الغاز في الاتجاه المعاكس للحركة، وفقًا لقانون حفظ كمية الحركة (يمكنك أيضًا قول القانون الثالث لنيوتن) يتحرك الصاروخ في اتجاه الحركة.
معرفة شرح عمل المحرك الصاروخ وحفظ كمية الحركة (أو القانون الثالث لنيوتن).
المحرك الصاروخي هو المحرك الذي ينبعث منه الغاز في الاتجاه المعاكس للحركة ، وفقًا لقانون حفظ كمية الحركة (يمكنك أيضًا قول القانون الثالث لنيوتن) نتيجة انبعاث الغاز ، يتحرك الصاروخ في اتجاه الحركة.
يعد مبدأ تشغيل محرك الصاروخ قضية
هامشية، تم تضمينه في الفصل الخاص بحفظ كمية الحركة.
في امتحانات البجروت في الفيزياء،
لا يُطلب من الطالب الإجابة بناءً على المعرفة العامة، جميع المواد (بما في ذلك
الدفع الصاروخي) تم تضمينها في المناهج الدراسية.
يمكن ايجاد تفسير عن الدفع الصاروخ
في اليوكيوب، في الوحدة التعليمية 24، في موضوع الانفجار والارتداد.
من المهم مراجعة جميع المواد
المدرجة في المنهاج، والتأكد من أنك بالفعل على دراية بجميع المواد. المنهاج موجود
على موقع Youcube على الصفحة الرئيسية في الشريط العلوي.
في نماذج امتحانات البجروت وفي المنهاج
الدراسي. يظهر موضوع الدفع الصاروخي في القسم 3.3 انقر هنا لتنزيل المنهاج الدراسي.
במבחני הגרות בפיזיקה תלמיד לא נדרש לענות על סמך ידע כללי, כל הנושאים(גם הנעה רקטית) נכללים בתכנית הלימודים.
ההסבר על הנעה רקטית נמצא ביוקיוב , בקיוב 24 ,בהתפוצצות ורתע.
חשוב לעבור על כל הנושאים הנכללים בתכנית הלימודים , ולוודא שאתם אכן מכירים את כל הנושאים. תכנית הלימודים נמצאת ביוקיוב בדף הבית בסרגל העליון
______________________________________________________________________________________
جـ.

______________________________________________________________________________________
...
التسارع يزداد.
يجب استخدام تعبير التسارع من القسم ب.
أثناء إطلاق الصاروخ ، يتم حرق الوقود. لذلك فإن كتلة الصاروخ تتناقص.
يمكنك أيضًا القول إن التسارع لا يتغير، وإهمال تغير
الكتلة نتيجة للتغير المهمل في كتلة الوقود.
______________________________________________________________________________________
______________________________________________________________________________________
...
المتجهات في الكينماتيكا في الحركة بمستوى وقوة الجاذبية.
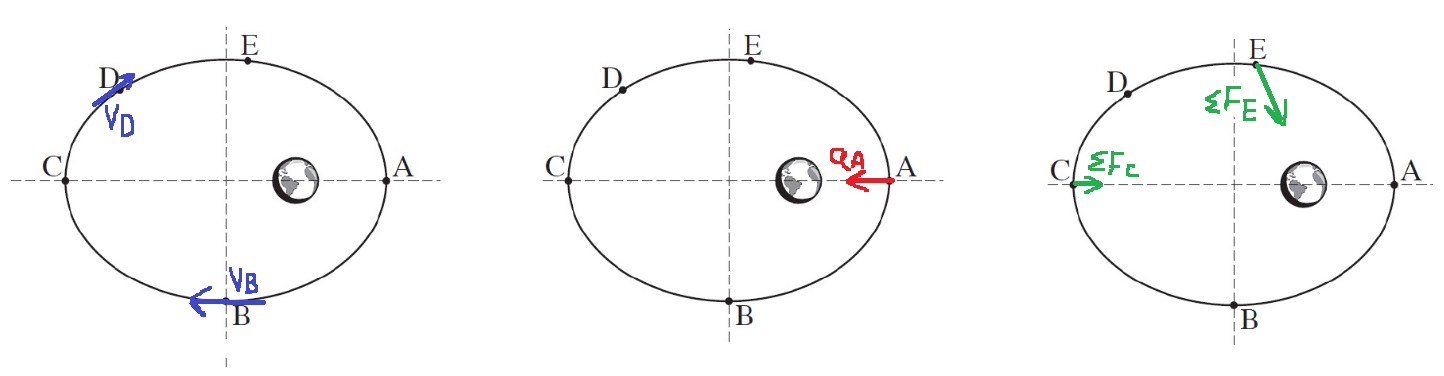
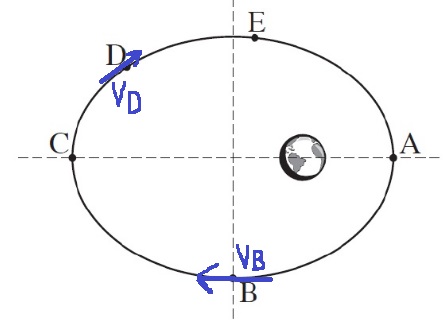
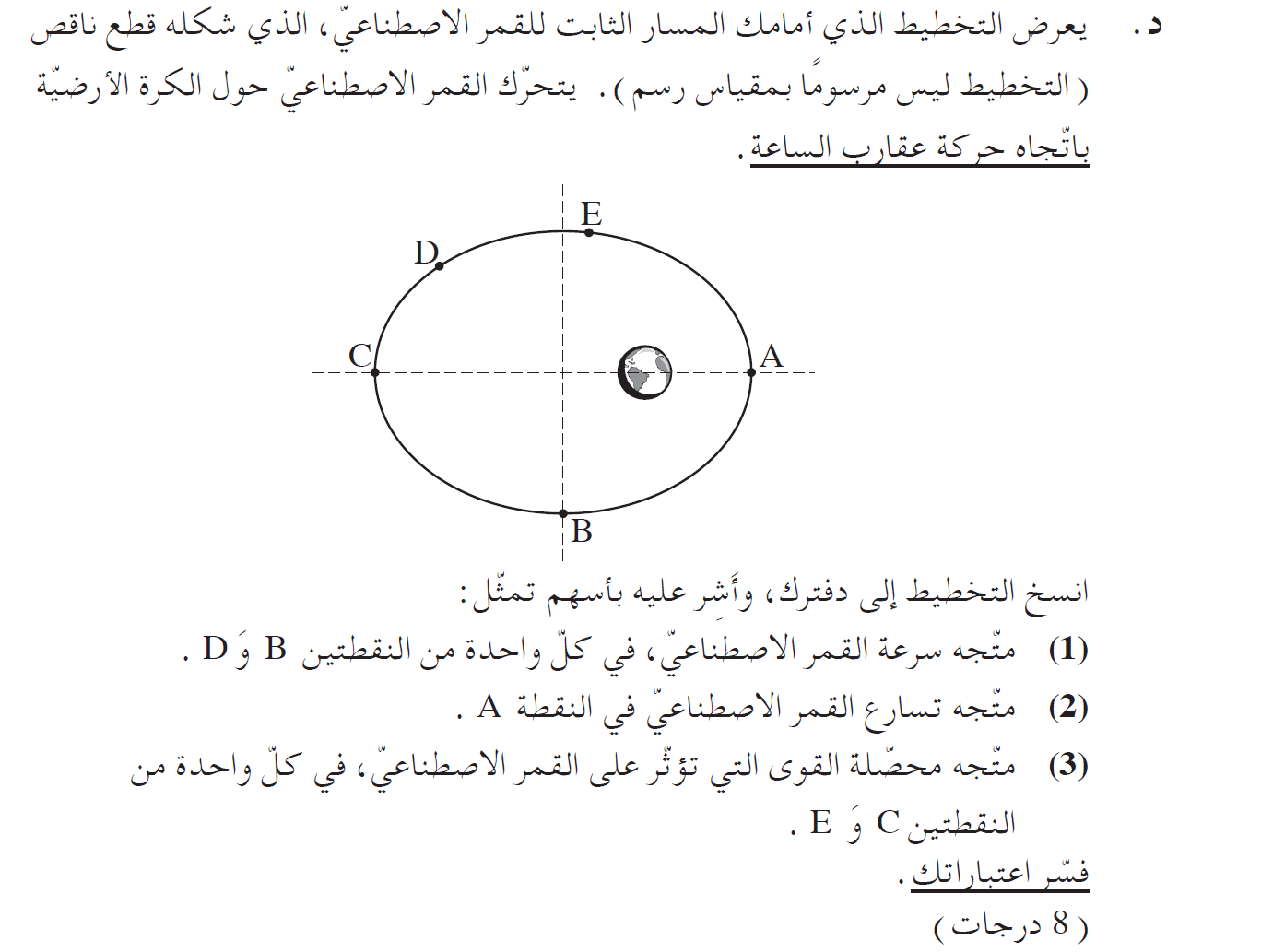
1- يكون متجه السرعة مماساً لمسار الحركة موجهاً بإتجاه الحركة. من القانون الثاني لكبلر ، كلما اقترب القمر الاصطناعي من الكرة الأرضية، زادت سرعته.
نحدد متجهات السرعة في النقطتين B و D:
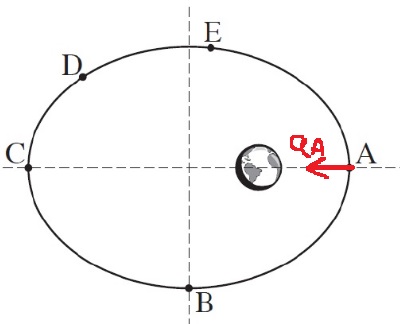
2- من القانون الثاني لنيوتن، اتجاه متجه التسارع هو اتجاه متجه محصّلة القوى. في هذه الحالة ، القوة الوحيدة المؤثرة هي قوة الجاذبية الموجهة نحو مركز الأرض.
نشير إلى متجه التسارع للقمر الاصطناعي في النقطة A:
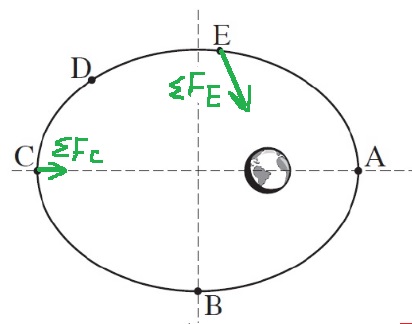
3- القوة المحصّلة هي قوة الجاذبية، من قوة الجاذبية العامة يمكن القول أنه كلما اقترب القمر الاصطناعي من الكرة الأرضية، زادت القوة ، واتجاه القوة نحو مركز الأرض.
نحدد متجهات القوة المحصّلة في النقطتين E و C:
נסמן את ווקטורי המהירויות בנקודות B ו- D:
2- מהחוק השני של ניוטון, כיוונו של וקטור התאוצה הוא ככיוון הווקטור השקול. במקרה זה הכוח היחיד הפועל הוא כוח הכובד, כיוונו אל מרכז כדור הארץ.
נסמן את וקטור התאוצה של הלוויין בנקודה A:
3-הכוח השקול הוא כוח הכובד, מכוח הכבידה האוניברסלי ניתן לומר שככל שהלוויין קרוב יותר לכדור כך הכוח יותר גדול, כיוון הכוח הוא אל מרכז כדוה"א.
נסמן את ווקטורי הכוח השקול בנקודות E ו- C:
1. من المهم توخي الحذر بشأن اتجاه المتجهات، في القسم 1
والقسم 3 ، يجب أيضًا توخي الحذر بشأن المقدار النسبي للمتجهات.
2. بشكل عام، للمتجهات لها مقياس رسم، عادة لا نحدد
المقياس ولا نستخدمه، لأننا عادة نتعامل فقط مع الجانب المفاهيمي.
يمكن أن يكون المقياس
مختلفًا، بحيث يكون متجه التسارع كبيرًا ويكون متجه القوة صغيرًا على الرغم من أن
الكتلة أكبر من 1 كغم.
2. באופן כללי , לווקטורים יש קנה מידה (למרות שאנחנו לא מציינים אותו) , קנה המידה יכול להיות שונה, כך שווקטור התאוצה יהיה גדול ו-וקטור הכוח יהיה קטן למרות שהמסה גדולה מ 1 ק"ג.
______________________________________________________________________________________
______________________________________________________________________________________
...
في النقطة A .
القانون الثاني لكبلر، معادلة الحركة ممكنة أيضًا.
السرعة القصوى في النقطة A. سرعة القمر الاصطناعي في النقطة E أقل من سرعة القمر الاصطناعي في النقطة A.
من القانون الثاني لكبلر - قانون المساحات المتساوية الذي ينص على أن الخط المستقيم الوهمي الذي يمر بين مركز القمر الاصطناعي والكوكب يغطي مساحات متساوية في أوقات متساوية ، وبالتالي ينص على أنه كلما اقترب القمر الاصطناعي من الكوكب الذي يدور حوله، زادت سرعة تحركه. النقطة A أقرب إلى الأرض ، وبالتالي فإن سرعة القمر الاصطناعي في النقطة A أكبر.
خيار آخر للتفكير: نكتب معادلة حركة قمر اصطناعي يتحرك في حركة دائرية حول الكرة الأرضية ، ونعبر عن السرعة كدالة لنصف قطر المدار.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«mrow»«mi mathvariant=¨bold¨»R«/mi»«menclose notation=¨downdiagonalstrike¨»«msup»«mrow»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/msqrt»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»
من التعبير يمكن ملاحظة أنه كلما كان نصف قطر المدار أصغر (البعد بين القمر الاصطناعي والأرض) زادت سرعة القمر الاصطناعي (وليس علاقة عكسية).
النقطة A هي الأقرب ، وبالتالي تكون السرعة ف هذه النقطة قصوى.
حل آخر:- عندما يتحرك القمر الاصطناعي من النقطة A إلى النقطة B ومن ثم إلى النقطة C تكون للقوة المحصّلة (قوة الجاذبية) التي تؤثر في اتجاه مركز الكرة الأرضية يكون لها دائمًا مركّب عكس اتجاه حركة القمر الاصطناعي مما يؤدي إلى انخفاض مقدار السرعة لذا كلما ابتعد القمر الاصطناعي من مركز الكوكب تقل سرعته، والعكس صحيح.
يمكن أيضًا حله بالاعتماد على حفظ الطاقة الميكانيكية الكلية: الطاقة الميكانيكية الكلية بالنقطة A الأقرب إلى مركز الكرة الأرضية مساوية للطاقة الميكانيكية الكلية في النقطة c الأبعد لمكز الكرة الأرضية، معلوم أنه كلما اقترب القمر الاصطناعي نحو مركز الكرة الأرضية تقل طاقته الوضعية حسب التعبير التالي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨».«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨».«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»r«/mi»«/mfrac»«/math»
حسب العلاقة اعلاه كلما قلّ البعد r من مركز الكوكب تزداد القيمة المطلقة للطاقة الوضعية ولكن بما أن قيمة الطاقة سالبة لذا قيمة الطاقة تقل كلما اقترب القمر الاصطناعي نحو مركز الكرة الأرضية، بما أن الطاقة الميكانيكية تبقى ثابتة لذا تزداد الطاقة الحركية كلما اقترب القمر الاصطناعي نحو الأرض أي تزداد سرعته.
מהחוק השני של קפלר- חוק השטחים השווים קובע שהישר העובר בין הלוויין לכוכב מכסה שטחים שווים בזמנים שווים , בכך הוא קובע שככל שהלווין קרוב יותר לכוכב סביבו הוא נע מהירותו גדולה יותר. הנקודה A יותר קרובה לכדור הארץ ,לכן מהירות הלוויין בנקודה A יותר גדולה.
אפשרות נוספת לנימוק: נכתוב את משוואת התנועה ללוויין הנע בתנועה לוויינית סביב כדור הארץ, ונבטא את המהירות בתלות ברדיוס מסלול התנועה.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«mrow»«mi mathvariant=¨bold¨»R«/mi»«menclose notation=¨downdiagonalstrike¨»«msup»«mrow»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/msqrt»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»
يتعامل السؤال مع سرعة القمر الاصطناعي في نقطتين
مختلفتين ، لكن السؤال ليس في أي من النقطتين تكون سرعة القمر الاصطناعي أكبر.
السؤال هو في أي نقطة تكون السرعة القصوى. لذلك، من
المهم أن نشير في التفسير أن النقطة A هي أقرب
نقطة في مدار القمر الاصطناعي حول الكرة الأرضية.
השאלה היא באיזו נקודה המהירות מרבית.
______________________________________________________________________________________
______________________________________________________________________________________