ألبوم الحلول في الجاذبية

في المرحلة الأولى ، يكون القمر الاصطناعي على ارتفاع 720 ألف متر فوق سطح الأرض. احسب تسارع الجاذبية في هذا الارتفاع.

تعمل الجاذبية العامة فقط على القمر الاصطناعي.

سنقوم بعمل رسم تخطيطي يصف ارتفاع القمر الاصطناعي فوق الأرض ، وقوة الجاذبية المؤثرة عليه.  

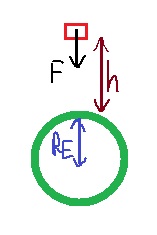
نجد تسارع القمر الصناعي من معادلة الحركة: 

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨»R«/mi»«/msub»«/math»

تسارع الجاذبية هو التسارع المركزي للقمر الاصطناعي ، ونعبر عن تسارعه من معادلة الحركة:

          «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«mrow»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»h«/mi»«msup»«mo mathvariant=¨bold¨»)«/mo»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»h«/mi»«msup»«mo mathvariant=¨bold¨»)«/mo»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»11«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»974«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»24«/mn»«/msup»«/mrow»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»38«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»720«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»3«/mn»«/msup»«msup»«mo mathvariant=¨bold¨»)«/mo»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»984«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»14«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»041«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»13«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»

1. تسارع السقوط الحر هو حقل الجاذبية الذييكّونه الكوكب، ولا يتعلق تسارع الجاذبية على حركة القمر الاصطناعي، فنحن نجد فقط التسارع من حركة القمر الاصطناعي. من الممكن إيجاد تسارع الجاذبية في النقطة التي يتحرك فيها القمر الاصطناعي بمساعدة كتلة فحص تتحرك في سقوط حر في خط مستقيم وتكون في ارتفاع تواجد القمر الاصطناعي.

2. تُحسب الجاذبية العامة وفقًا لبعد القمر الاصطناعي من مركز الكرة الأرضية، وليس وفقًا لارتفاع القمر الاصطناعي. لكي لا نخطئ ، من المهم رسم مخطّط.

3. يُشار إلى تسارع الجاذبية (أو حقل الجاذبية) في أي نقطة غير موجودة على سطح الأرض بالرمز *g.

1. يمكنك إيجاد السرعة المماسية باستخدام معادلة الحركة.

2. عند إيجاد السرعة، يجب أيضًا تحديد اتجاهها، ما لم يتم كتابة مقدار السرعة، وفي هذه الحالة يتم كتابة السرعة المماسية.

  يبدو أنهم يسألون فقط عن مقدار السرعة وليس عن اتجاه الحركة. بعد إيجاد مقدار السرعة، من الأفضل ملاحظة أن اتجاه السرعة مماس للحركة.

نتطرّق لكل قول من الأقوال:

القول 1- طاقة وضع الجاذبية سالبة وتتناسب عكسياً على البعد بين الجسمين:

 «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/math»

             في المرحلة الأولى، كلما كان القمر الاصطناعي أبعد، كلما قلت الطاقة الوضعية السالبة، وبالتالي فإن هذا القول صحيح.

القول 2-  حركة القمر الاصطناعي، تتعلق الطاقة الحركية بنصف قطر مدار القمر الاصطناعي وفقًا لما يلي:

   «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«/math»

            في المرحلة الأولى ، يكون نصف قطر مدار القمر الاصطناعي أكبر، وبالتالي تكون طاقته الحركية أصغر. القول غير صحيح. 

القول 3 - في حركة القمر الاصطناعي، تتعلق الطاقة الميكانيكية الكلية بنصف قطر المسار وفقًا لما يلي:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«/math»

             في المرحلة الأولى وفي المرحلة الثانية، يختلف نصف قطر المسار، وبالتالي فإن الطاقة الميكانيكية الكلية مختلفة، والقول غير صحيح.

1. يجب الانتباه لإشارة الطاقة السالبة. الطاقة التي تساوي ناقص اثنين جول أكبر من طاقة تساوي ألف جول.

2. ليست هناك حاجة لتطوير تعبيرات الطاقة لحركة القمر الاصطناعي ، فالتعبيرات موجودة في ملحق القوانين المرفق في امتحان البجروت.

لكي يغادر القمر الصناعي مجال جاذبية الكوكب الذي يتحرك حوله ، يجب أن تكون طاقته الكلية موجبة. أو على الأقل صفر.

إصغر طاقة المطلوب إضافتها للقمر الاصطناعي هو الطاقة التي تلزم حتى تصبح الطاقة الميكانيكية للقمر الاصطناعي صفراً بعد الإضافة.

احسب طاقة قمر اصطناعي وزنه 300 كغم يتحرك في دائرة نصف قطرها  6900 كم.

نستخدم التعبير عن إ الطاقة الملائمة لحركة القمر الاصطناعي:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»11«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»974«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»24«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»300«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»66«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/math»

لذلك ، الطاقة الإضافية المطلوبة:  «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»66«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/math», إذن الطاقة الكلية ستكون صفر جول.