______________________________________________________________________________________
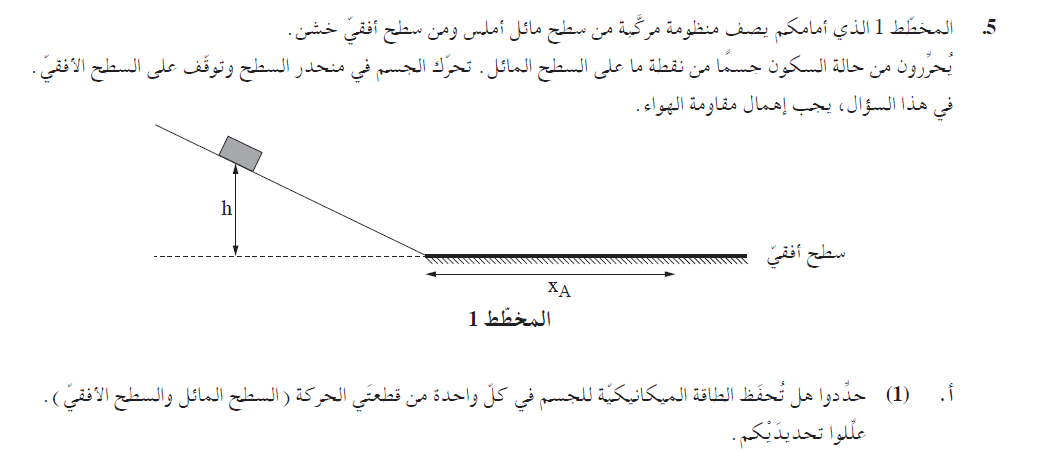
...
على السطح المائل يتحقق حفظ الطاقة الميكانيكية.
على السطح الأفقي لا يتم حفظ الطاقة الميكانيكية.
במשטח האופקי האנרגיה המכנית לא נשמרת.
يتم حفظ الطاقة الميكانيكية فقط عندما تكون القوى الوحيدة التي تبذل شغلاً على الجسم هي قوى الحافظة (مثل الجاذبية).
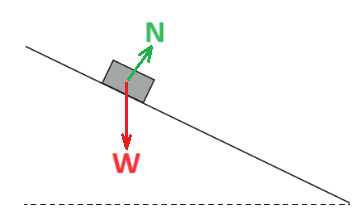
أثناء حركة الجسم في منحدر السطح المائل، تؤثر قوتان على الجسم: قوة الجاذبية والقوة العمودية. كما هو مبين في الشكل التالي:
تعمل القوة العمودية باتجاه عمودي على الحركة، ومن تعريف الشغل فإن القوة العمودية لا تبذل شغلًا، بل قوة الجاذبية فقط هي التي تبذل شغلًا.
وبما أنه في حركة الجسم في منحدر السطح المائل فإن قوة الجاذبية فقط هي التي تبذل شغلًا، وبالتالي تُحفط لطاقة الميكانيكية.
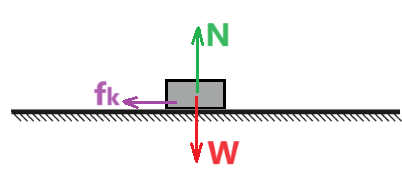
أثناء حركة الجسم على السطح الأفقي (غير الأملس) تؤثر على الجسم ثلاث قوى: قوة الجاذبية، والقوة العمودية، وقوة الاحتكاك. كما هو مبين في الشكل التالي:
تؤثر القوة العمودية وقوة الجاذبية باتجاه عمودي على الحركة، ولا تبذل أي شغل. تعمل قوة الاحتكاك عكس اتجاه الحركة وتبذل شغلاً سالبًا.
لأنه أثناء حركة الجسم على السطح الأفقي يتم بذل شغلًا على الجسم بواسطة قوة غير حافظة (قوة الاحتكاك)، وفي حركة الجسم على السطح الأفقي لا تُحفظ الطاقة الميكانيكية .
כוח הנורמל פועל בניצב לתנועה, מהגדרת העבודה כוח הנומרל לא מבצע עבודה, רק כוח הכובד מבצע עבודה.
מכיוון שבתנועת הגוף במורד המישור רק כוח הכובד עושה עבודה האנרגיה המכנית נשמרת.
בתנועת הגוף במשטח האופקי (הלא חלק), פועלים על הגוף שלושה כוחות: כוח הכובד, כוח הנורמל וכוח החיכוך. כמוראה באיור הבא:
כוח הנורמל וכוח הכובד פועלים בניצב לתנועה, הם לא מבצעים עבודה. כוח החיכוך פועל נגד כיוון התנועה הוא מבצע עבודה שלילית.
מכיוון שבתנועת הגוף במשטח האופקי מבוצעת על הגוף עבודה של כוח לא משמר(כוח החיכוך) , בתנועת הגוף במשטח האופקי האנרגיה המכנית לא נשמרת.
1. من تعريف الشغل : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mstyle mathvariant=¨bold¨ mathcolor=¨#FF0000¨»«mo stretchy=¨true¨»|«/mo»«mi»F«/mi»«mo stretchy=¨true¨»|«/mo»«/mstyle»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mstyle mathvariant=¨bold¨ mathcolor=¨#FF0000¨»«mo stretchy=¨true¨»|«/mo»«mrow»«mo»§#8710;«/mo»«mi»X«/mi»«/mrow»«mo stretchy=¨true¨»|«/mo»«/mstyle»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«/math»، يمكن ملاحظة أنه عندما تؤثر القوة بشكل عمودي على الحركة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathvariant=¨bold¨ mathcolor=¨#FF0000¨»«mo stretchy=¨true¨»(«/mo»«mrow»«mi»§#945;«/mi»«mo»=«/mo»«mn»90«/mn»«mo»§#176;«/mo»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«/math» القوة لا تُنجز شغلًا.
ومن ثم، فإن القوى العمودية المؤثرة على الجسم أثناء حركته، على السطح المائل وعلى السطح الأفقي، لا تبذل شغلًا.
2. لا تعمل القوة العمودية دائمًا باتجه عمودي على الحركة، لذلك على سبيل المثال عندما يصطدم جسم بجدار، فإن القوة العمودية التي يؤثر بها الجدار على الجسم ليست بالضرورة متعامدة مع الحركة.
3. تُحفظ الطاقة دائما، دون استثناء ودون أي شروط. الطاقة الميكانيكية لا تُحفظ دائما.
شرط حفظ الطاقة الميكانيكية هو: أن جميع القوى التي تبذل شغلاً على الجسم المتحرك هي قوى حافظة.
4. من تعبير شغل القوى الغير حافظة والذي يظهر في صفحات القوانين:
ويمكن القول أنه إذا لم يتم بذل شغل بواسطة قوى غير حافظة فلا يحدث تغير في الطاقة الميكانيكية، بمعنى آخر: سوف تُحفظ الطاقة الميكانيكية.
5. القوة الحافظة هي القوة التي لا يتعلق شغلها على المسار الذي يتحرك فيه القوة، ففي المسار المغلق يكون شغل القوة الحافظة صفرًا.
هناك ثلاث قوى حافظة: قوة الجاذبية، والقوة المرنة التي يُؤثر بها النابض، والقوة الكهربائية.
6. قبل استخدام معادلة حفظ الطاقة الميكانيكية، من الضروري معرفة سبب حفظ الطاقة الميكانيكية.
لذلك، من المهم معرفة شرط حفظ الطاقة الميكانيكية: جميع القوى التي تبذل شغلًا على الجسم المتحرك هي قوى حافظة.
לכן כוחות הנורמל הפועלים על הגוף בתנועתו, במישור המשופע ובמשטח האופקי, לא מבצעים עבודה.
2. כוח הנורמל לא תמיד פועל בניצב לתנועה , כך למשל כאשר גוף מתנגש בקיר כוח הנורמל שהקיר מפעיל על הגוף הוא לא בהכרח ניצב לתנועה.
3.האנרגיה תמיד נשמרת, ללא יוצא מהכלל וללא כל תנאי. לא תמיד האנרגיה המכנית נשמרת.
התנאי לשימור אנרגיה מכנית הוא: שכל הכוחות המבצעים עבודה על הגוף הנע הם כוחות משמרים.
3. כוח משמר הוא כוח שעבודתו לא תלויה במסלול לאורכו פועל הכוח, במסלול סגור עבודת כוח משמר היא אפס.
קיימים שלושה כוחות משמרים: כוח הכובד, כוח אלסטי שמפעיל קפיץ , וכוח חשמלי.
4. לפני שימוש במשוואת שימור האנרגיה המכנית יש לנמק מדוע האנרגיה המכנית נשמרת.
לכן, חשוב להכיר את התנאי לשימור אנרגיה מכנית: כל הכוחות המבצעים עבודה על הגוף הנע הם כוחות משמרים.
______________________________________________________________________________________

______________________________________________________________________________________
...
لا تُحفظ كمية الحركة.
من تعريف كمية الحركة: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#FF6600¨»«mi mathvariant=¨bold¨»P«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»§#183;«/mo»«mover mathcolor=¨#FF6600¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/math», لا يتم حفظ كمية الحركة لجسم واحد فقط إذا لم تتغير كتلة الجسم ولم تتغير سرعته.
كمية حركة الجسم يساوي كتلة الجسم مضروبة في سرعته: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»P«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/mstyle»«/math».
يتحرك الجسم في منحدر السطح المائل بتسارع ثابت، وتزداد سرعته. ولذلك، أثناء حركة الجسم في منحدر السطح المائل، لا يتم حفظ كمية الحركة.
وفي حركة الجسم على السطح الأفقي سوف تقل سرعة الجسم. ولذلك، حتى أثناء حركة الجسم على السطح الأفقي، لا يتم حفظ كمية الحركة للجسم.
حسب قانون كمية الدفع وكمية الحركة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»J«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»P«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/math» ينتج أنه حتى يتحقق حفظ كمية الحركة يجب أن يكون كمية الدفع للقوى الخارجية التي تعمل على الجسم مساوية لصفر، عندما يتحرك الجسم في منحدر السطح المائل فإن محصلة القوى الخارجية تعمل على الجسم نحو منحدر السطح المائل هذا يعني أن هنالك كمية دفع خارجي تعمل على الجسم نحو الأسفل لذا سوف تزداد كمية الحركة نحو الأسفل.
في حركة الجسم على السطح الأفقي تعمل محصلة قوى عكس حركة الجسم وهي قوة الاحتكاك لهذا تعمل كمية دفع على الجسم باتجاه عكس حركة الجسم مما يؤدي إلى نقصان كمية حركة الجسم.
הגוף נע במורד המישור המשופע בתאוצה קבועה, מהירותו גדלה. לכן, בתנועת הגוף במורד המישור התנע לא נשמר.
בתנועת הגוף במשטח האופקי מהירות הגוף קטנה. לכן, בתנועת הגוף במשטח האופקי התנע של הגוף לא נשמר.
1. يستخدم مصطلح "حفظ كمية الحركة" في منظومة متعددة الأجسام، في أحداث مثل: الاصطدام، الانفجار، الارتداد، إلخ.
يتم حفظ كمية الحركة للمنظومة عندما تتأثر حركة الأجسام بالقوى الداخلية فقط.
يستخدم في هذا القسم مصطلح "حفظ كمية الحركة" بشكل استثنائي، حيث أن السؤال يتناول جسم واحد.
تُحفظ كمية حركة الجسم إذا لم تتغير كتلته ولم تتغير سرعته أيضًا.
2. يجب أن يُفهم من مبادئ الديناميكا أن سرعة الجسم تتغير في في منحدر السطح المائل وعلى السطح الأفقي.
3. كمية الحركة هو مقدار متّجه، وله اتجاه. في الحالة التي يتحرك فيها الجسم بسرعة متغيرة الاتجاه وليس في المقدار (مثل الحركة الدائرية المنتظمة السرعة)
تتغير كمية حركة الجسم، ولا تُحفظ كمية الجسم.
התנע של המערכת נשמר כאשר תנועת הגופים מושפעת מכוחות פנימיים בלבד.
בסעיף זה נעשה שימוש חריג במושג "שימור תנע", מכיוון שהשאלה עוסקת בגוף בודד.
התנע של הגוף נשמר אם מסתו לא משתנה וגם מהירותו לא משתנה.
2. יש להבין מעקרונות הדינמיקה שמהירות הגוף משתנה במוד המישור ובמשטח האופקי .
3. התנע הוא ווקטור, יש לו כיוון. במקרה שבו גוף נע במהירות המשתנה בכיוונה ולא בגודלה (כמו תנועה מעגלית קצובה)
התנע של הגוף משתנה, תנע הגוף לא נשמר.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mstyle»«/math»
لا يتم حفظ الطاقة الميكانيكية، يجب استخدام تعبير شغل القوى الغير حافظة.
أثناء حركة الجسم من نقطة تحريره على السطح المائل إلى نقطة التوقف على السطح الأفقي، لا يتم حفظ الطاقة الميكانيكية نتيجة شغل قوة الاحتكاك.
نكتب تعبير لشغل القوة الغير الحافظة ونعبر عن معامل الاحتكاك الحركي منها:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1581;§#1575;§#1601;§#1592;§#1577;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1594;§#1610;§#1585;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1602;§#1608;§#1609;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«/math»
نصف الطاقة الوضعية للجسم بالنسبة إلى مستوى الإنتساب الموجود على ارتفاع السطح الأفقي.
وفي نهاية الحركة يتوقف الجسم على السطح الأفقي، ولا يكون للجسم طاقة حركية ولا طاقة وضع.
في بداية الحركة، يكون لدى الجسم طاقة وضع الجاذبية فقط.
وفقًا لذلك نكتب التعبير عن شغل القوى الغير الحافظة بشكل صريح.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«msub»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«/math»
قوة الاحتكاك تعمل عكس اتجاه الحركة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»180«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#176;«/mo»«/math» .
في الاتجاه العمودي على السطح الأفقي يكون الجسم في حالة إتّزان، والقوة العمودية تساوي قوة الجاذبية المؤثرة على الجسم.
نتطرّق إلى حركة الجسم على السطح الأفقي بالنسبة إلى المحور الذي نقطة أصله في بداية السطح واتجاهه هو اتجاه الحركة.
بحيث تكون الغزاحة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«/math» .
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«msub»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»E«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»h«/mi»«msub»«mi mathvariant=¨bold¨»X«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
نُعوّض القيم المعطاة ونحسب معامل الاحتكاك الحركي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»h«/mi»«msub»«mi mathvariant=¨bold¨»X«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
נכתוב את ביטוי עבודת הכוח הלא משמר נבטא ממנו את מקדם החיכוך הקינטי:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mprescripts/»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#1502;§#1513;§#1502;§#1512;§#1497;§#1501;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1500;§#1488;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1499;§#1493;§#1495;§#1493;§#1514;«/mi»«/mrow»«none/»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«/math»
נתאר את האנרגיה הפוטנציאלית של הגוף ביחס למישור ייחוס הממוקם בגובה המשטח האופקי.
בסיום התנועה הגוף נעצר על המשטח האופקי, אין לגוף אנרגיה קינטית ואנרגיה פוטנציאלית .
בתחילת התנועה יש לגוף רק אנרגיה פוטנציאלית כובדית.
נכתוב בהתאם את ביטוי עבודת הכוח הלא משמר בצורה מפורשת.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«msub»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«/math»
כוח החיכוך פועל נגד כיוון התנועה ,«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»180«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#176;«/mo»«/math» .
בכיוון הניצב למשטח האופקי הגוף מתמיד בתנועתו , כוח הנורמל שווה לכוח הכובד הפועל על הגוף.
נתייחס לתנועת הגוף במשטח האופקי ביחס לציר שראשיתו בתחילת המשטח וכיוונו ככיוון התנועה.
כך שהעתק התנועה שווה ל «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«/math» .
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«msub»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»E«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»h«/mi»«msub»«mi mathvariant=¨bold¨»X«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
נציב את הערכים הנתונים ונחשב את מקדם החיכוך הקינטי:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»h«/mi»«msub»«mi mathvariant=¨bold¨»X«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
1. في الحالات التي تُحفظ فيها الطاقة (فقط قوة حافظة هي التي تبذل شغلًا) يجب استخدام معادلة حفظ الطاقة.
في الحالات التي لا تُحفظ فيها الطاقة (توجد قوة غير حافظة تبذل شغلاً) يجب استخدام تعبير الشغل للقوة الغير الحافظة.
2. في علم الحركة (الكينيماتيكا)، لا يمكن كتابة تعبير واحد لحركات مختلفة، يمكن كتابة معادلة حفظ الطاقة وتعبير القوة الغير حافظة لحركات مختلفة أيضًا.
3. هناك نوعان من معاملات الاحتكاك: معامل الاحتكاك الحركي ومعامل الاحتكاك الساكن. يصف السؤال حركة الجسم، لذا على الرغم من أنه يقول فقط "احسب معامل الاحتكاك" إلا أنه يجب أن يكون مفهومًا أن الإشارة هي إلى معامل الاحتكاك الحركي.
4.تُؤثر قوة الاحتكاك على الجسم على السطح الأفقي، ويجب عليك استخدام القوة العمودية المؤثرة على الجسم على السطح الأفقي وليس القوة العمودية المؤثرة على الجسم على السطح المائل.
5. طريقة أخرى: التعبير عن معامل الاحتكاك الحركي من معادلة الحركة.
نعمل مخطط للقوى التي تعمل على الجسم:
نكتب معادلات الحركة. نتطرق إلى المحورx الموجه في اتجاه الحركة إلى اليمين
والمحور Y موجه عموديًا إلى الأعلى:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«/math»
نُعبر عن معامل الاحتكاك من معادلة الحركة العمودية
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«/math»
لحساب تسارع الجسم على السطح الأفقي، يتم حساب سرعة الجسم في أسفل السطح باستخدام معادلة حفظ الطاقة.
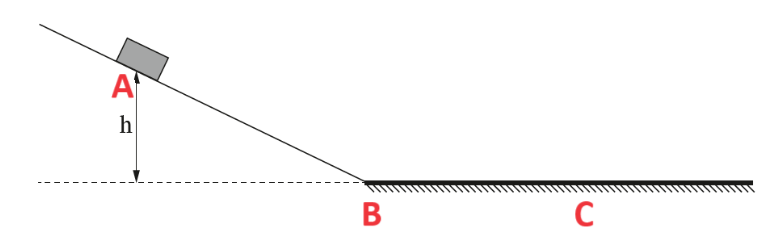
نُشير إلى نقطة تحرير الجسم بـ A، ونقطة أسفل المستوى بـ B، والنقطة التي توقف فيها الجسم بـ C.
نكتب معادلة حفظ الطاقة لحركة الجسم على السطح المائل، ونعبر منها عن السرعة في النقطة B:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«msub»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»h«/mi»«/msqrt»«/math»
ونعبر عن التسارع على السطح الأفقي حتى يتوقف من تعبير مربع السرعات:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»X«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mn mathvariant=¨bold¨»0«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«msup»«mrow»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«msqrt»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»h«/mi»«/msqrt»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»X«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»h«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»X«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»h«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»X«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mfrac»«/math»
نعوّض تعبير التسارع في تعبير معامل الاحتكاك:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»a«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mfrac mathcolor=¨#FF0000¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»h«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»X«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mfrac»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»h«/mi»«msub»«mi mathvariant=¨bold¨»X«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
במקרים בהם האנרגיה לא נשמרת (יש כוח לא משמר המבצע עבודה) יש להשתמש בביטוי עבודת הכוח הלא משמר.
2. בקינמטיקה לא ניתן לכתוב ביטוי אחד לתנועות שונות , ניתן לכתוב את משוואת שימור האנרגיה ואת ביטוי הכוח הלא משמר גם לתנועות שונות.
3. יש שני סוגים של מקדמי חיכוך: מקדם חיכוך קינטי ומקדם חיכוך סטטי.
בשאלה מתוארת תנועת הגוף,לכן למרות שכתוב רק "חשבו את מקדם החיכוך" יש להבין שהכוונה היא למקדם החיכוך הקינטי.
4. כוח החיכוך מבצע עבודה על הגוף במשטח האופקי יש להשתמש בכוח הנורמל הפועל על הגוף במשטח האופקי ולא בכוח הנורמל הפועל על הגוף במישור הנטוי.
______________________________________________________________________________________

______________________________________________________________________________________
...
سيقطع الجسم B مسافة مساوية للمسافة التي يقطعها الجسم A.
من التعبير عن حركة الجسم على السطح الأفقي كدالة للارتفاع الذي تم تحرير الجسم منه، يمكن التعرف على علاقة الازاحة بكتلة الجسم.
نعبر عن ازاحة الجسم بدلالة معامل الاحتكاك في القسم السابق:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»h«/mi»«msub»«mi mathvariant=¨bold¨»X«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»X«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mi mathvariant=¨bold¨»h«/mi»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«/mfrac»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
ازاحة الجسم على السطح الأفقي لا تتعلق بكتلة الجسم، وبالتالي فإن ازاحة حركة الجسم B على السطح الأفقي تساوي ازاحة حركة الجسم A.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»h«/mi»«msub»«mi mathvariant=¨bold¨»X«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»X«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mi mathvariant=¨bold¨»h«/mi»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«/mfrac»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
העתק התנועה במשטח האופקי לא תלוי במסת הגוף, לכן העתק תנועת גוף B במשטח האופקי שווה להעתק תנועת גוף A.
التعبير عن تسارع الجسم عندما يتحرك في منحدر السطح المائل هو: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«/math» , أي أن تسارع الجسم أثناء حركة الجسم في منحدر السطح المائل الأملس لا تتعلق على كتلة الجسم.
والتعبير عن تسارع الجسم في سطح أفقي غير أملس هو: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»g«/mi»«/math» , حركة الجسم على السطح الأفقي لا تتعلق بكتلة الجسم. ولذلك فإن ازاحة الحركة على السطح الأفقي لا تتعلق بكتلة الجسم.
וביטוי התאוצה של הגוף במישור אופקי לא חלק הוא: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»g«/mi»«/math» , תנועת הגוף במשטח האופקי לא תלויה במסת הגוף.
לכן העתק התנועה במשטח האופקי לא תלוי במסת הגוף.
______________________________________________________________________________________

______________________________________________________________________________________
...
مقدار كمية الدفع 2.4 نيوتن في الثانية واتجاهها نحو اليسار.
إيجاد كمية الحركة باستخدام قانون كمية الحركة وكمية الدفع.
نقوم برسم تخطيطي يصف كميتي الدفع التي تعمل على الجسمين أثناء الاصطدام.
نُشير إلى كمية الدفع الذي يُؤثره الجسم A على الجسم B بـ «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨28px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»AB«/mi»«/msub»«/mstyle»«/math» وكمية الدفع الذي يُؤثره الجسم B على الجسم A بـ- «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨28px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»BA«/mi»«/msub»«/mstyle»«/math».
نكتب قانون الدفع وكمية الحركة على الجسم B:
نُشير إلى سرعة الجسم B قبل الاصطدام بـ- «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«/mstyle»«/math» ولسرعة الجسم B بعد الاصطدام بـ- «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«/mstyle»«/math».
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»AB«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»AB«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»AB«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«/mstyle»«/math»
كتلة الجسم B وسرعته قبل الاصطدام معطاة في السؤال.
نحسب سرعة الجسم B بعد الاصطدام باستخدام اعتبارات الطاقة وكمية الحركة.
يصطدم الجسمان إصطدامًا مرنًا، لنفترض أن الاصطدام أحادي البعد، نستخدم تعبير فرق السرعة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/mstyle»«/math»
قبل الاصطدام كان الجسم A في حالة سكون:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»4«/mn»«/menclose»«/mstyle»«/math»
زمن الاصطدام قصير جدًا، لذلك يمكن افتراض أن القوى الداخلية المؤثرة أثناء الاصطدام أكبر بكثير من قوة الاحتكاك.
نكتب معادلة حفظ كمية الحركة مع إهمال قوة الاحتكاك:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/menclose»«/mstyle»«/math»
معادلتي حفظ الطاقة الحركية وحفظ كمية الحركة معادلتان بمجهولين.
نُعوّض قيمة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«/mstyle»«/math» من معادلة حفظ الطاقة الحركية في معادلة حفظ كمية الحركة، ونحسب «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«/mstyle»«/math»:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»4«/mn»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/menclose»«/mstyle»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨»«mo stretchy=¨true¨»(«/mo»«mrow»«msub»«mi mathcolor=¨#FF0000¨»U«/mi»«mi mathcolor=¨#FF0000¨»B«/mi»«/msub»«mo mathcolor=¨#FF0000¨»+«/mo»«mn mathcolor=¨#FF0000¨»4«/mn»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨»«msub»«mi»U«/mi»«mi»B«/mi»«/msub»«mo»+«/mo»«mn»1«/mn»«mo».«/mo»«mn»6«/mn»«/mstyle»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mstyle»«/math»
نحسب وفقًا لذلك الدفع الذي أثر على الجسم B:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»AB«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«/mstyle»«/math»
وبالتالي فإن مقدار الدفع هو 2.4 نيوتن في الثانية واتجاهه نحو اليسار عكس اتجاه المحور.
1.هناك تعبيران فقط يتناولان الدفع، تعريف الدفع: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»J«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mover mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«/math» وقانون الدفع وكمية الحركة: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»J«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mover mathcolor=¨#FF0000¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»P«/mi»«/mrow»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/math»
لم يتم تحديد زمن تأثير الدفع، لذلك يجب استخدام قانون الدفع وكمية الحركة.
2. ينص قانون الدفع وكمية الحركة على أن الدفع المؤثر على جسم معين يساوي التغير في كمية حركة ذلك الجسم.
في حالة الاصطدام بين جسمين، من المهم الانتباه إلى عدم مقارنة الدفع المؤثر على الجسم B مع التغير في كمية الحركة للجسم A.
3. لا يتم حفظ كمية الحركة إلا عندما تتأثر حركة الجسمين بالقوى الداخلية فقط.
وبما أن الجسمين يتحركان على سطح غير أملس أثناء الاصطدام، فإن قوى الاحتكاك تؤثر على الجسمين (بالإضافة إلى القوى الداخلية)، وبالتالي لا يتم حفظ كمية الحركة.
لا يمكن حل هذا السؤال دون استخدام معادلة حفظ كمية الحركة، لذلك مكتوب في السؤال أن زمن الاصطدام قصير جداً.
من تعريف الدفع: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»J«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mover mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«/math» , يمكن ملاحظة أنه في دفع معين يؤثر على الجسم، كلما قصرزمن تأثير القوة، زادت القوة.
كتب محرّر السؤال أن زمن الاصطدام قصير جداً لأنه يريد من الممتحن أن يفترض أن أنه يتحقق حفظ كمية الحركة لأن دفع قوة الاحتكاك يكون مهمل.
4. تعبير فرق السرعات: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mover mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«msub»«mover mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mrow mathcolor=¨#FF0000¨»«mo mathvariant=¨bold¨»(«/mo»«msub»«mover»«mi mathvariant=¨bold¨»U«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mover»«mi mathvariant=¨bold¨»U«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mstyle»«/math» لا يمكن استخدامه إلا في حالة الاصطدام الذي يتم فيه حفظ الطاقة الحركية .
تلائم المعادلة أيضًا الاصطدام الذي تكون فيه كتلة الأجسام مختلفة، ولكن فقط في الاصطدام أحادي البعد. يظهر التعبير الخاص بفرق السرعة في صفحات القوانين:
5. لحساب سرعة الجسم B بعد الاصطدام، يمكنك استخدام معادلة حفظ الطاقة بدلاً من معادلة فرق السرعة
لا ينصح بهذا، لأنه في معادلة حفظ الطاقة الحركية هي معادلة من الدرجة الثانية، وهذا يكون أصعب رياضيًا.
6. أثناء الاصطدام، يؤثر الجسم A على الجسم B بقوة إلى اليسار، ومن تعريف الدفع: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»J«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mover mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«/math» اتجاه الدفع هو اتجاه القوة
ولذلك فإن اتجاه الدفع هو إلى اليسار..
عند حساب الدفع باستخدام قانون الدفع وكمية الحركة، يتم الحصول على دفع سالب، مما يعني أن اتجاه الدفع هو عكس اتجاه المحور المحدّد،وبما أنه في السؤال أن اتجاه المحور هو إلى اليمين، فإن اتجاه الدفع هو إلى اليسار.
זמן פעולת המתקף לא נתון , לכן יש להשתמש במשפט התנע מתקף.
2. משפט תנע מתקף קובע שהמתקף הפועל על גוף מסוים שווה לשינוי התנע של אותו גוף.
בהתנגשות מעורבים שני גופים , חשוב לשים לב לא להשוות בין המתקף הפועל על גוף B בשינוי תנע של גוף A.
3. התנע נשמר רק כאשר תנועת הגופים מושפעת מכוחות פנימיים בלבד.
מכיוון שהגופים נעים על משטח לא חלק בזמן ההתנגשות פועלים על הגופים כוחות חיכוך (בנוסף לכוחות הפנימיים) לכן, התנע לא נשמר.
לא ניתן לפתור שאלה זו ללא שימוש במשוואת שימור התנע , לכן כתוב בשאלה שזמן ההתנגשות הוא קצר מאוד.
מהגדרת המתקף: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»J«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mover mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«/math» , ניתן לראות שבמתקף מסויים הפועל על הגוף ככל שזמן פעולת הכוח קטן יותר כך הכוח גדול יותר.
עורך השאלה כתב שזמן ההתנגשות קצר מאוד מכיוון שהוא רוצה שהנבחן יניח שהכוחות הפנימיים הם גדולים
כוח החיכוך זניח ביחס לכוחות הפנימיים, וניתן להשתמש בשימור התנע.
______________________________________________________________________________________

______________________________________________________________________________________
...
التعبير الصحيح هو التعبير 2.
من قانون الدفع وكمية الحركة، لكي يكون مقدار الدفع هو نفسه في كلتا المرتين، يجب أن يكون مقدار تغير كمية الحركة هو نفسه في كلتا المرتين.
أثناء حركة الجسم في منحدر السطح المائل، تعمل قوة الجاذبية فقط، وبالتالي يتم حفظ الطاقة الميكانيكية في هذه الحركة.
وبما أن الجسم يتحرك في كلتا الحالتين بنفس السرعة (من حالة السكون) وعلى نفس الارتفاع H، فمن مبدأ حفظ الطاقة تكون سرعة الجسم أثناء حركة الجسم في منحدر السطح المائل هي نفسها في المرتين.
مقدار التغير في كمية الحركة في المرة الأولى هو نفس مقدار التغير في كمية الحركة في المرة الثانية، وبالتالي من قانون الدفع وكمية الحركة فإن مقدار الدفع هو نفسه في كلتا الحالتين.
التعبير الصحيح هو التعبير 2.
מכיוון שבשני הפעמים הגוף נע מאותה המהירות (ממנוחה) ומאותו גובה H , משימור אנרגיה מהירות הגוף בתחתית המישור היא זהה בשני הפעמים.
גודל שינוי התנע בפעם הראשונה זהה לגודל שינוי התנע בפעם השנייה, לכן ממשפט התנע מתקף גודל המתקף זהה בשני המקרים.
הביטוי הנכון הוא ביטוי 2.
1. لم يذكر في السؤال من يُؤثر الدفع، فالإشارة إلى الدفع الذي تعمله قوة الجاذبية.
2. لأنه في كل مرة تختلف زاوية ميل السطح المائل، يختلف اتجاه متجه سرعة الجسم في أسفل السطح في كل مرة.
مقدار التغيّر في كمية الحركة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathvariant=¨bold¨ mathcolor=¨#FF0000¨»«mo stretchy=¨true¨»|«/mo»«mover»«mrow»«mo»§#8710;«/mo»«mi»P«/mi»«/mrow»«mo»§#8594;«/mo»«/mover»«mo stretchy=¨true¨»|«/mo»«/mstyle»«/math» متساوٍ في كلتا المرتين لكن اتجاه متجه تغيّر كمية الحركة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#FF0000¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»P«/mi»«/mrow»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/math» مختلفًا.
لذلك، مقدار الدفع «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathvariant=¨bold¨ mathcolor=¨#FF0000¨ mathsize=¨20px¨»«mo stretchy=¨true¨»|«/mo»«mover»«mi»J«/mi»«mo»§#8594;«/mo»«/mover»«mo stretchy=¨true¨»|«/mo»«/mstyle»«/math»متساوٍ في المرتين. لكن متجه الدفع «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mover mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»J«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/mstyle»«/math» هو مختلف.
ومن المهم أن نلاحظ أن السؤال يتناول مقدار الدفع وليس الدفع.
2. בגלל שבכל פעם זווית נטיית המישור היא שונה, כיוון וקטור מהירות הגוף בתחתית המישור הוא שונה בכל פעם.
גודל שינוי התנע «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathvariant=¨bold¨ mathcolor=¨#FF0000¨»«mo stretchy=¨true¨»|«/mo»«mover»«mrow»«mo»§#8710;«/mo»«mi»P«/mi»«/mrow»«mo»§#8594;«/mo»«/mover»«mo stretchy=¨true¨»|«/mo»«/mstyle»«/math» הוא זהה בשני הפעמים , אך וקטור שינוי התנע «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#FF0000¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»P«/mi»«/mrow»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/math» הוא שונה.
בהתאם, גודל המתקף «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathvariant=¨bold¨ mathcolor=¨#FF0000¨ mathsize=¨20px¨»«mo stretchy=¨true¨»|«/mo»«mover»«mi»J«/mi»«mo»§#8594;«/mo»«/mover»«mo stretchy=¨true¨»|«/mo»«/mstyle»«/math» הוא זהה בשני הפעמים. אך המתקף «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mover mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»J«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/mstyle»«/math» הוא שונה.
חשוב לשים לב לכך שהשאלה עוסקת בגודל המתקפים ולא במתקפים.
______________________________________________________________________________________