______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨»W«/mi»«mi mathvariant=¨bold¨»N«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»J«/mi»«/mstyle»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨»W«/mi»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»10«/mn»«mi mathvariant=¨bold¨»J«/mi»«/mstyle»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨»W«/mi»«mi mathvariant=¨bold¨»mg«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»10«/mn»«mi mathvariant=¨bold¨»J«/mi»«/math»
تعريف الشغل.
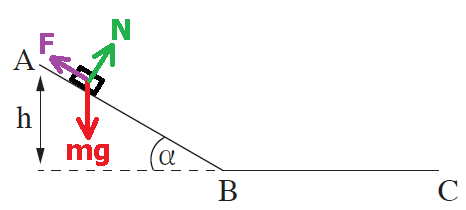
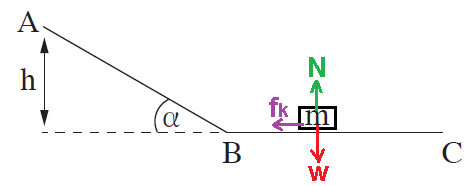
يتحرك الجسم لأعلى المستوى المائل الأملس، على طول القطعة AB.
تؤثر ثلاث قوى على الجسم: قوة الجاذبية والقوة العمودية والقوة F.
نحسب شغل القوة العمودية باستخدام تعريف الشغل :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»COS«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math»
تعمل القوة العمودية باتجاه عمودي على الحركة، والزاوية بين اتجاه الحركة واتجاه القوة العمودية تساوي 90 درجة. نحسب وفقا لذلك شغل القوة العمودية.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»COS«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»90«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/math»
إذن، شغل القوة العمودية يساوي صفر جول.
نحسب شغل الجاذبية باستخدام تعريف الشغل:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»COS«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»mg«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mi mathvariant=¨bold¨»mg«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»COS«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math»
الزاوية بين قوة الجاذبية واتجاه الحركة (اتجاه متجه السرعة) 120 درجة. كما هو مبيّن في الشكل التالي:
نعبر بطريقة هندسية عن الازاحة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»AB«/mi»«/msub»«/mstyle»«/math» من النقطة B إلى النقطة A:
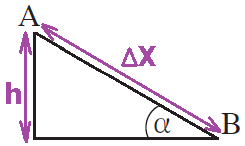
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»h«/mi»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»X«/mi»«mi mathvariant=¨bold¨»AB«/mi»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»AB«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»h«/mi»«mrow»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mrow»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»30«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«/math»
نحسب شغل قوة الجاذبية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»mg«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»|«/mo»«mi mathvariant=¨bold¨»mg«/mi»«mo stretchy=¨true¨ mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo stretchy=¨true¨ mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»COS«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»mg«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»120«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mspace linebreak=¨newline¨/»«/math»
إذن، شغل قوة الجاذبية يساوي ناقص عشرة جول.
על הגוף פועלים שלושה כוחות: כוח הכובד , כוח הנורמל והכוח F.
נחשב את עבודת כוח הנורמל בעזרת הגדרת העבודה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»COS«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math»
כוח הנורמל פועל בניצב לתנועה, הזווית בין כיוון התנועה לכיוון כוח הנורמל שווה ל 90 מעלות. נחשב בהתאם את עבודתו.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»COS«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»90«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/math»
לכן עבודת כוח הנורמל שווה לאפס ג'אול.
נחשב את עבודת כוח הכובד בעזרת הגדרת העבודה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»COS«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»mg«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mi mathvariant=¨bold¨»mg«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»COS«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math»
הזווית בין כוח הכובד לכיוון התנועה (כיוון ווקטור המהירות) היא 120 מעלות. כפי שניתן לראות באיור הבא:
נבטא גיאומטרית את העתק התנועה «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»AB«/mi»«/msub»«/mstyle»«/math» מנקודה B לנקודה A:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»h«/mi»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»X«/mi»«mi mathvariant=¨bold¨»AB«/mi»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»AB«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»h«/mi»«mrow»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mrow»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»30«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«/math»
נחשב את עבודת כוח הכובד:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»mg«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»|«/mo»«mi mathvariant=¨bold¨»mg«/mi»«mo stretchy=¨true¨ mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo stretchy=¨true¨ mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»COS«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»mg«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»120«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mspace linebreak=¨newline¨/»«/math»
לכן עבודת כוח הכובד שווה למינוס עשר ג'אול.
1. في الحالة التي تكون فيها القوة العمودية تعمل بشكل عمودي على الحركة، فإن الشغل الذي تقوم به القوة العمودية يساوي صفرًا.
2. لا تعمل القوة العمودية دائمًا بشكل عمودي على الحركة، على سبيل المثال عندما يتحرك الجسم المتحرر من حالة السكون نحو الأسفل ويضرب الأرض.
في اللحظة التي تصطدم فيها الكرة بالأرض، لا تعمل القوة العمودية باتجاه عمودي على الحركة.
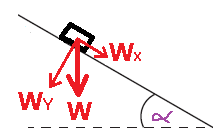
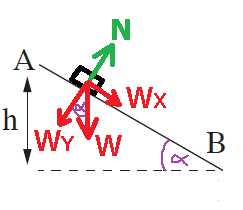
3. الشغل المبذول بواسطة قوة الجاذبية يمكن إيجاده بعد تحليل قوة الجاذبية إلى مركبتها القائمتين.
مركّب قوة الجاذبية WX تعمل عكس اتجاه الحركة لذا تبذل شغل سالب. مركّب قوة الجاذبية WY تعمل باتجاه عمودي للحركة، لذا لا يبذل شغلاً
شغلل قوة الجاذبية يساوي شغل مركّب قوة الجاذبية WX نحسب مركّب الشغل لقوة الجاذبية WX:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mrow mathcolor=¨#FF0000¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»|«/mo»«mi mathvariant=¨bold¨»F«/mi»«mo stretchy=¨true¨ mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mrow mathcolor=¨#FF0000¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«mo stretchy=¨true¨ mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#920;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»W«/mi»«mi mathvariant=¨bold¨»x«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mrow mathcolor=¨#FF0000¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»|«/mo»«msub»«mi mathvariant=¨bold¨»W«/mi»«mi mathvariant=¨bold¨»x«/mi»«/msub»«mo stretchy=¨true¨ mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mrow mathcolor=¨#FF0000¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»X«/mi»«mi mathvariant=¨bold¨»AB«/mi»«/msub»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»180«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»W«/mi»«mi mathvariant=¨bold¨»x«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»mg«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»X«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»AB«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»180«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»mg«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»X«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»AB«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»W«/mi»«mi mathvariant=¨bold¨»x«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»J«/mi»«/mstyle»«/math»
4. يمكن إيجاد شغل قوة الجاذبية من التغير في الطاقة الوضعية.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»mg«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»G«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»G«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»G«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»mg«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»J«/mi»«/mstyle»«/math»
2. לא תמיד כוח הנורמל פועל בניצב לתנועה , לדוגמה כאשר גוף משוחרר ממנוחה נע כלפי מטה ופוגע ברצפה.
ברגע פגיעת הכדור ברצפה כוח הנורמל לא פועל בניצב לתנועה.
______________________________________________________________________________________
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1603;§#1604;§#1610;«/mi»«mi mathvariant=¨bold¨»W«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mstyle»«/math»
قانون الشغل والطاقة.
نحسب الشغل الكلي للقوى المؤثرة على الجسم باستخدام قانون الشغل والطاقة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/mstyle»«/math»
لذلك ، فإن الشغل الكلي هو صفر.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/mstyle»«/math»
לכן, העבודה הכוללת שווה לאפס.
1. يسمى جزء الحركة الأملس AB ، لكن الجسم يتحرك من النقطة B إلى النقطة A.
عند حساب التغير في الطاقة الحركية، يجب حساب الفرق بين الطاقة الحركية في النهاية (في النقطة B) والطاقة الحركية في البداية (في النقطة A).
2. يجب التمييز بين قانون الشغل والطاقة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#FF0000¨ notation=¨box¨»«mi mathvariant=¨bold¨»W«/mi»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«/menclose»«/mstyle»«/math» لتعبير شغل القوى غير الحافظة: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«menclose mathcolor=¨#FF0000¨ notation=¨box¨»«msub»«mrow/»«mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1581;§#1575;§#1601;§#1592;§#1577;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1594;§#1610;§#1585;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1602;§#1608;§#1609;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1588;§#1594;§#1604;«/mi»«/mrow»«/msub»«mi mathvariant=¨bold¨»W«/mi»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»E«/mi»«/menclose»«/mstyle»«/math»
تتناول عبارة عمل القوى غير الحافظة شغل القوى غير الحافظة ، وليس الشغلل الكلي.
3. الشغل الكلي يساوي مجموع شغل جميع القوى: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mrow/»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1575;§#1604;§#1603;§#1604;§#1610;«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»N«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»mg«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»F«/mi»«/msub»«/mstyle»«/math»
وجدنا في القسم السابق شغل القوة العمودية وشغل الجاذبية.
لكن، لا توجد معطيات كافية عن القوة F ولا يمكن استخدام تعبير الشغل لحساب شغلها.
4. عندما تكون السرعة النهائية مساوية للسرعة الابتدائية، فإن الشغل المحصل يساوي صفرًا، حتى لو كان محصلة القوى لا يساوي صفرًا طوال زمن الحركة.
בחישוב השינוי האנרגיה הקינטית יש לחשב את ההפרש שבין האנרגיה הקינטית בסוף (בנקודה B) לאנרגיה הקינטית בהתחלה(בנקודה A).
2. יש להבחין בין משפט העבודה אנרגיה «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#FF0000¨ notation=¨box¨»«mi mathvariant=¨bold¨»W«/mi»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«/menclose»«/mstyle»«/math» לביטוי עבודת הכוחות הלא משמרים: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«menclose mathcolor=¨#FF0000¨ notation=¨box¨»«mmultiscripts»«mi mathvariant=¨bold¨»W«/mi»«mprescripts/»«mrow»«mi mathvariant=¨bold¨»§#1502;§#1513;§#1502;§#1512;§#1497;§#1501;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1500;§#1488;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1499;§#1493;§#1495;§#1493;§#1514;«/mi»«/mrow»«none/»«/mmultiscripts»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»E«/mi»«/menclose»«/mstyle»«/math»
ביטוי עבודת הכוחות הלא משמרים עוסק בעבודת הכוחות הלא משמרים, לא בעבודה בעבודה הכוללת.
3. העבודה הכוללת שווה לסכום העבודות: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mprescripts/»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1499;§#1493;§#1500;§#1500;§#1514;«/mi»«none/»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»N«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»mg«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»F«/mi»«/msub»«/mstyle»«/math»
בסעיף הקודם מצאנו את עבודת הנורמל ואת עבודת כוח הכובד.
אך, אין מספיק נתונים על הכוח F לא ניתן להשתמש בביטוי העבודה לחישוב עבודתו.
4. כאשר המהירות הסופית שווה למהירות ההתחלתית העבודה הכוללת שווה לאפס, גם אם שקול הכוחות לא שווה לאפס כל זמן התנועה.
______________________________________________________________________________________
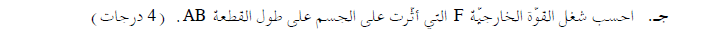
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨»W«/mi»«mi mathvariant=¨bold¨»F«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»10«/mn»«mi mathvariant=¨bold¨»J«/mi»«/mstyle»«/math»
الشغل الكلي يساوي مجموع شغل القوى الخارجية، لذلك يمكن التعبير عن شغل القوة الخارجية بالاعتماد على الشغل الكلي.
طريقة أخرى: القوة الخارجية هي قوة غير حافظة يكون شغلها مساويًا للتغير في الطاقة الميكانيكية الكلية.
דרך נוספת: הכוח החיצוני הוא כוח לא משמר עבודתו שווה לשינוי באנרגיה המכנית הכוללת.
نكتب الشغل الكلي كمجموع شغل القوى الخارجية. والتعبير عن شغل القوة الخارجية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«maction mathcolor=¨#0000FF¨ actiontype=¨argument¨»«mrow/»«/maction»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1603;§#1604;§#1610;«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»mg«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mprescripts/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1603;§#1604;§#1610;«/mi»«none/»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»mg«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/mstyle»«/math»
طريقة أخرى: القوة الخارجية F هي القوة الوحيدة الغير حافظة وتبذل شغل.
سنجد شغل القوة الخارجية باستخدام تعبير شغل القوى غير الحافظة: F
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mprescripts/»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#1581;§#1575;§#1601;§#1592;§#1577;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1594;§#1610;§#1585;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1602;§#1608;§#1609;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«none/»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»EK«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»EK«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
يبدأ الجسم في التحرك من حالة السكون وفي نهاية حركته يكون في حالة سكون. الطاقة الحركية في بداية ونهاية الحركة تساوي الصفر.
نكتب الطاقات الوضعية بصورة مفصّلة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»F«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»EK«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»A«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»EK«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»B«/mi»«/msub»«/menclose»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»F«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»mgh«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»mgh«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»B«/mi»«/msub»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»F«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»mg«/mi»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»«mo stretchy=¨true¨»(«/mo»«msub»«mi»h«/mi»«mi»A«/mi»«/msub»«mo»-«/mo»«msub»«mi»h«/mi»«mi»B«/mi»«/msub»«mo stretchy=¨true¨»)«/mo»«/mstyle»«/math»
نختار مستوى الانتساب في ارتفاع النقطة B «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨16px¨»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨»«mo stretchy=¨true¨»(«/mo»«mrow»«msub»«mi»h«/mi»«mi»B«/mi»«/msub»«mo»=«/mo»«mn»0«/mn»«mi»m«/mi»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«/mstyle»«/math», ارتفاع النقطة A معطى في السؤال.
نحسب شغل القوة F وفقًا لذلك.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»F«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»mg«/mi»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»«mo stretchy=¨true¨»(«/mo»«msub»«mi»h«/mi»«mi»A«/mi»«/msub»«mo»-«/mo»«msub»«mi»h«/mi»«mi»B«/mi»«/msub»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»F«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»mg«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»h«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»J«/mi»«/math»
إذن ، الشغل المبذول بواسطة القوة الخارجية F يساوي 10 جول.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mprescripts/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1499;§#1493;§#1500;§#1500;§#1514;«/mi»«none/»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»mg«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mprescripts/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1499;§#1493;§#1500;§#1500;§#1514;«/mi»«none/»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»mg«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/mstyle»«/math»
דרך נוספת: הכוח החיצוני F הוא הכוח היחידי שהוא לא משמר ומבצע עבודה.
נמצא את עבודת הכוח החיצוני בעזרת ביטוי עבודת הכוחות הלא משמרים:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mprescripts/»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#1502;§#1513;§#1502;§#1512;§#1497;§#1501;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1500;§#1488;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1499;§#1493;§#1495;§#1493;§#1514;«/mi»«/mrow»«none/»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»EK«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»EK«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
הגוף מתחיל לנוע מנוחה ובסיום התנועה הוא נמצא במנוחה. האנרגיות הקינטית בתחילת התנועה ובסיומה שווה לאפס.
נכתוב את האנרגיות הפוטנציאליות בצורה מפורשת:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»F«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»EK«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»A«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»EK«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»B«/mi»«/msub»«/menclose»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»F«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»mgh«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»mgh«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»B«/mi»«/msub»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»F«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»mg«/mi»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»«mo stretchy=¨true¨»(«/mo»«msub»«mi»h«/mi»«mi»A«/mi»«/msub»«mo»-«/mo»«msub»«mi»h«/mi»«mi»B«/mi»«/msub»«mo stretchy=¨true¨»)«/mo»«/mstyle»«/math»
נקבע את מישור הייחוס בגובה הנקודה B «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨16px¨»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨»«mo stretchy=¨true¨»(«/mo»«mrow»«msub»«mi»h«/mi»«mi»B«/mi»«/msub»«mo»=«/mo»«mn»0«/mn»«mi»m«/mi»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«/mstyle»«/math», גובה הנקודה A נתון בשאלה.
נחשב בהתאם את עבודת הכוח F.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»F«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»mg«/mi»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»«mo stretchy=¨true¨»(«/mo»«msub»«mi»h«/mi»«mi»A«/mi»«/msub»«mo»-«/mo»«msub»«mi»h«/mi»«mi»B«/mi»«/msub»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»F«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»mg«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»h«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»J«/mi»«/math»
1. في الميكانيكا، هناك قوتان حافظتان فقط: القوة التي يشغلها النابض وقوة الجاذبية. جميع القوى الأخرى هي قوى غير حافظة.
2. التغيير في الطاقة الميكانيكية الكلية يساوي مجموع شغل القوى غير الحافظة.
لأن القوة F هي القوة الوحيدة غير الحافظة التي تأثر. شغلها يساوي التغيير في الطاقة الميكانيكية.
3. تعمل القوة F في اتجاه الحركة وبالتالي فهي تبذل شغلاً موجباً.
4. يعتمد حساب شغل القوة F على مجموع الشغل على نتائج الحسابات في البنود السابقة.
في أسئلة البجروت ، في كثير من الأحيان ، يعتمد حل بند معين على بند سابق.
2. השינוי באנרגיה המכנית כוללת שווה לסכום עבודות הכוחות הלא משמרים.
מכיוון שהכוח F הוא הכוח הלא משמר היחידי שמבצע עבודה. עבודתו שווה לשינוי באנרגיה המכנית.
3. חישוב עבודת הכוח F מסכום העבודות מבוסס על תוצאות החישובים בסעיפים הקודמים.
בשאלות הבגרות, פעמים רבות, הפתרון של סעיף מסוים מתבסס על סעיף קודם.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»32«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mstyle»«/math»
حفظ الطاقة الميكانيكية.
طريقة أخرى: الديناميكا والحركية.
דרך נוספת: דינמיקה קינמטיקה.
في حركة الجسم من النقطة A إلى النقطة B فقط قوة الجاذبية هي التي تبذل شغل ، وبالتالي يتم حفظ الطاقة الميكانيكية.
سنكتب معادلة حفظ الطاقة، ونعبر منها بسرعة الجسم عند النقطة B:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«/mstyle»«/math»
يتوقف الجسم توقفًا لحظيًا في النقطة A ، والطاقة الحركية في النقطة A تساوي صفرًا.
نكتب معادلة حفظ الطاقة بشكل مفصّل ونجد سرعة الجسم في النقطة B:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«msub»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mstyle mathvariant=¨bold¨»«mn»10«/mn»«mo»§#183;«/mo»«mn»2«/mn»«/mstyle»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»40«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»32«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mstyle»«/math»
طريقة أخرى: يتحرك الجسم لأسفل المستوى المائل بتسارع ثابت.
نرسم مخطط القوى:
نكتب معادلات الحركة، ونشير إلى المحور X الموجه لأسفل المستوى، والمحور Y المتعامد على المستوى:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/mstyle»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»mg«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«/mstyle»«/math»
نحسب التسارع من معادلة الحركة في اتجاه المحور X:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/math»
نجد سرعة الجسم في النقطة B باستخدام تعبير مربع السرعات:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«msup»«mn mathvariant=¨bold¨»0«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»4«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»40«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»32«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mstyle»«/math»
إذن ، سرعة الجسم في النقطة B تساوي 6.32 مترًا في الثانية.
נכתוב את משוואת שימור האנרגיה, ונבטא ממנה את מהירות הגוף בנקודה B:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«/mstyle»«/math»
הגוף נעצר רגעית בנקודה A , האנרגיה הקינטית בנקודה A שווה לאפס.
נכתוב את משוואת שימור האנרגיה בצורה מפורשת ונמצא את מהירות הגוף בנקודה B:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«msub»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mstyle mathvariant=¨bold¨»«mn»10«/mn»«mo»§#183;«/mo»«mn»2«/mn»«/mstyle»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»40«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»32«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mstyle»«/math»
1. من المهم أن نفهم تمامًا كل مرحلة من المراحل المختلفة، وأن نفهم أي من القوى تعمل في كل مرحلة. هذا مهم للغاية في تحليل الحركة في كل مرحلة.
في هذا السؤال ، عندما يتحرك الجسم لأعلى المستوى المائل، تعمل القوة غير الحافظة F ، وبالتالي لا يتم حفظ الطاقة الميكانيكية.
عندما يتحرك الجسم لأسفل المستوى لا تعمل القوة F ، تعمل قوة الجاذبية فقط ، وبالتالي يتم حفظ الطاقة الميكانيكية.
2. لحساب سرعة الجسم في النقطة B، يتم إجراء عملية جذر، وبالتالي هناك إجابتان للسرعة، ويتم تحديد إشارة السرعة وفقًا لاتجاه الحركة بالنسبة للمحور.
اخترنا المحور الذي يكون موجهًا في اتجاه لأسفل المستوى، وبالتالي فإن سرعته موجبة.
3. بالتمارين، يوصى بمحاولة حل كل سؤال بعدة طرق. في الاختبار، حتى لا تضيع الوقت، يوصى بحلها بطريقة واحدة.
בשאלה זו, כאשר הגוף נע במעלה המישור פועל כוח לא משמר F, לכן האנרגיה המכנית לא נשמרת.
כאשר הגוף נע במורד המישור הכוח F לא פועל, רק כוח הכובד מבצע עבודה, לכן האנרגיה המכנית נשמרת.
2. לחישוב מהירות הגוף בנקודה B מתבצעת פעולת שורש, לכן יש שתי תשובות למהירות , סימן המהירות נקבע בהתאם לכיוון התנועה ביחס לציר.
בחרנו ציר שכיוונו בכיוון מורד המישור, לכן מהירותו חיובית.
3. בתרגול מומלץ לנסות לפתור כל שאלה במספר דרכים. במבחן, כדי לא לבזבז זמן, מומלץ לפתור בדרך אחת.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»E«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»m«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»g«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»h«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»mg«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»X«/mi»«/math»
يجب استخدام قانون الشغل والطاقة لحركة الجسم في المستوى الأفقي ، ويجب التعبير عن الطاقة الحركية في النقطة B كدالة لـ h من حفظ الطاقة عند حركة الجسم لأسفل المستوى المائل.
نرسم مخطط للقوى المؤثرة على الجسم عندما يتحرك الجسم في المستوى الأفقي:
تعمل قوة الاحتكاك، ولا يتم حفظ الطاقة الميكانيكية.
نكتب قانون الشغل والطاقة.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»E«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«/msub»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»fk«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»E«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«/msub»«mspace linebreak=¨newline¨/»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mi mathvariant=¨bold¨»fk«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»180«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«/msub»«/mstyle»«/math»
للحصول على تعبير يتعلق بـ X (كما هو محدد في السؤال) نصف حركة الجسم بالنسبة لمحور أفقي نقطة أصله النقطة B واتجاهه باتجاه الحركة، بحيث تكون قيمة X مساوية لازاحة الحركة.
نُشير للطاقة الحركية للجسم في الموقع X بـ EK ، ونكتب قانون الشغل والطاقة لجسم يتحرك من النقطة B إلى الموقع X
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mi mathvariant=¨bold¨»fk«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»180«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«/msub»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»180«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«/msub»«/mrow»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»mg«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
للحصول على تعبير للطاقة الحركية كدالة للارتفاع h، نعبر من معادلة حفظ الطاقة أسفل المستوى عن الطاقة الحركية في النقطة B كدالة لـ h:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«msub»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«/mstyle»«/math»
نكتب تعبيرًا للطاقة الحركية كدالة لـ X:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»mg«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»mg«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»h«/mi»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»mg«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/menclose»«/mstyle»«/math»
1. في هذا القسم ، يجب تطوير التعبير ، لذلك يجب وصف مكان الجسم بشكل عام بمساعدة X.
2. بعد إيجاد التعبير، يوصى بفحص الوحدات ومطابقة التعبير بالرسم البياني.
3. التعبير منطقي، يمتلك الجسم طاقة حركية عند النقطة B عندما تكون X = 0m. وعندما يتحرك الجسم للأمام ، تزداد قيمة X ، وتنخفض سرعة الجسم ، وتنخفض الطاقة الحركية للجسم.
4. في هذه الحالة، إذا استخدمنا تعبير شغل القوة غير الحافظة بدلاً من قانون الشغل والطاقة، سنتوصل إلى تعبير مماثل.
(يتحرك الجسم في مستوى أفقي ، والتغير في الطاقة الميكانيكية هو تغير في الطاقة الحركية فقط، وبالإضافة إلى ذلك ، فإن قوة الاحتكاك هي القوة الوحيدة التي تبذل شغلًا).
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow mathcolor=¨#FF0000¨»«msub»«maction actiontype=¨argument¨»«mrow/»«/maction»«mrow»«mi mathvariant=¨bold¨»§#1581;§#1575;§#1601;§#1592;§#1577;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1594;§#1610;§#1585;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1602;§#1608;§#1609;«/mi»«/mrow»«/msub»«mi mathvariant=¨bold¨»W«/mi»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»E«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨»W«/mi»«mi mathvariant=¨bold¨»fk«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»E«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»mg«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»U«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»EK«/mi»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»EK«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»mg«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨»=«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»U«/mi»«/menclose»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»EK«/mi»«mo mathvariant=¨bold¨»-«/mo»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»h«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»h«/mi»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»mg«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/menclose»«/mrow»«/mstyle»«/math»
2. לאחר מציאת הביטוי מומלץ לבדוק יחידות והתאמת הביטוי לגרף.
3. במקרה זה , אם נשתמש בביטוי עבודת כוח לא משמר במקום במשפט העבודה אנרגיה נגיע לביטוי זהה.
______________________________________________________________________________________
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mstyle»«/math»
يتعامل الرسم البياني مع التعبير الذي تم الحصول عليه في القسم السابق، ويجب مقارنة قيمة الميل في الرسم البياني بتعبير الميل.
من تعبير الطاقة الحركية كدالة لـ X: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»mg«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/mstyle»«/math» يمكن تحديد أن تعبير الميل في الرسم البياني هو: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»mg«/mi»«/math»
نحسب قيمة ميل الخط الموضح في الرسم البياني لنقطتين على الخط المستقيم : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mn mathvariant=¨bold¨»5«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»J«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/mstyle»«/math»
נשווה בין ביטוי השיפוע לערכו, نحسب معامل الاحتكاك الحركي من ميل الدالة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»mg«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»2«/mn»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨ mathsize=¨20px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»2«/mn»«/mrow»«mrow»«mo mathvariant=¨bold¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»mg«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathsize=¨20px¨»2«/mn»«mrow»«mn mathvariant=¨bold¨ mathsize=¨20px¨»0«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»5«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»10«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathsize=¨20px¨»2«/mn»«mn mathvariant=¨bold¨ mathsize=¨20px¨»5«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»4«/mn»«/math»
لذلك ، فإن معامل الاحتكاك الحركي يساوي 0.4 .
נחשב את ערך שיפוע הישר המתואר בגרף משתי נקודות על הישר: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1513;§#1497;§#1508;§#1493;§#1506;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mn mathvariant=¨bold¨»5«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»J«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/mstyle»«/math»
נשווה בין ביטוי השיפוע לערכו, ונחשב את מקדם החיכוך הקינטי:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»mg«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»2«/mn»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨ mathsize=¨20px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»2«/mn»«/mrow»«mrow»«mo mathvariant=¨bold¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»mg«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathsize=¨20px¨»2«/mn»«mrow»«mn mathvariant=¨bold¨ mathsize=¨20px¨»0«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»5«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»10«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathsize=¨20px¨»2«/mn»«mn mathvariant=¨bold¨ mathsize=¨20px¨»5«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»4«/mn»«/math»
לכן, מקדם החיכוך הקינטי שווה ל 0.4 .
1. عندما يُعطى أي رسم بياني ونتعامل مع التعبير الموصوف في الرسم البياني ، يظهر سؤال بشكل دائم تقريبًا، وللإجابة عليه، يجب مقارنة قيمة الميل بتعبير الميل.
2. يوجد للميل وحدات. عند حساب قيمة الميل، يجب كتابة وحدات الميل.
بشكل عام ، وحدات الميل تساوي وحدات المحور العمودي مقسومة على وحدات المحور الأفقي.
2. לשיפוע יש יחידות. בחישוב ערך השיפוע יש לכתוב את יחידות השיפוע.
באופן כללי, יחידות השיפוע שוות ליחידות הציר האנכי חלקי יחידות הציר האופקי.
______________________________________________________________________________________