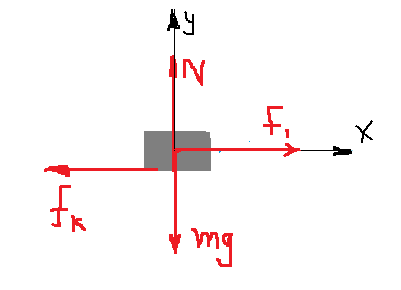
الحلول والمنتديات لـ"ألبوم الحلول" في موضوع كمية الحركة والطاقة: 2009,4- صندوق يتحرك بحركات مختلفة

20. 2009,4- صندوق يتحرك بحركات مختلفة

______________________________________________________________________________________

...

لكي يتحرك الصندوق بطاقة حركية ثابتة على سطح غير أملس ، يجب أن تؤثر عليه قوة بالإضافة إلى قوة الاحتكاك في اتجاه الحركة على الصندوق.

القانون الأول لنيوتن.

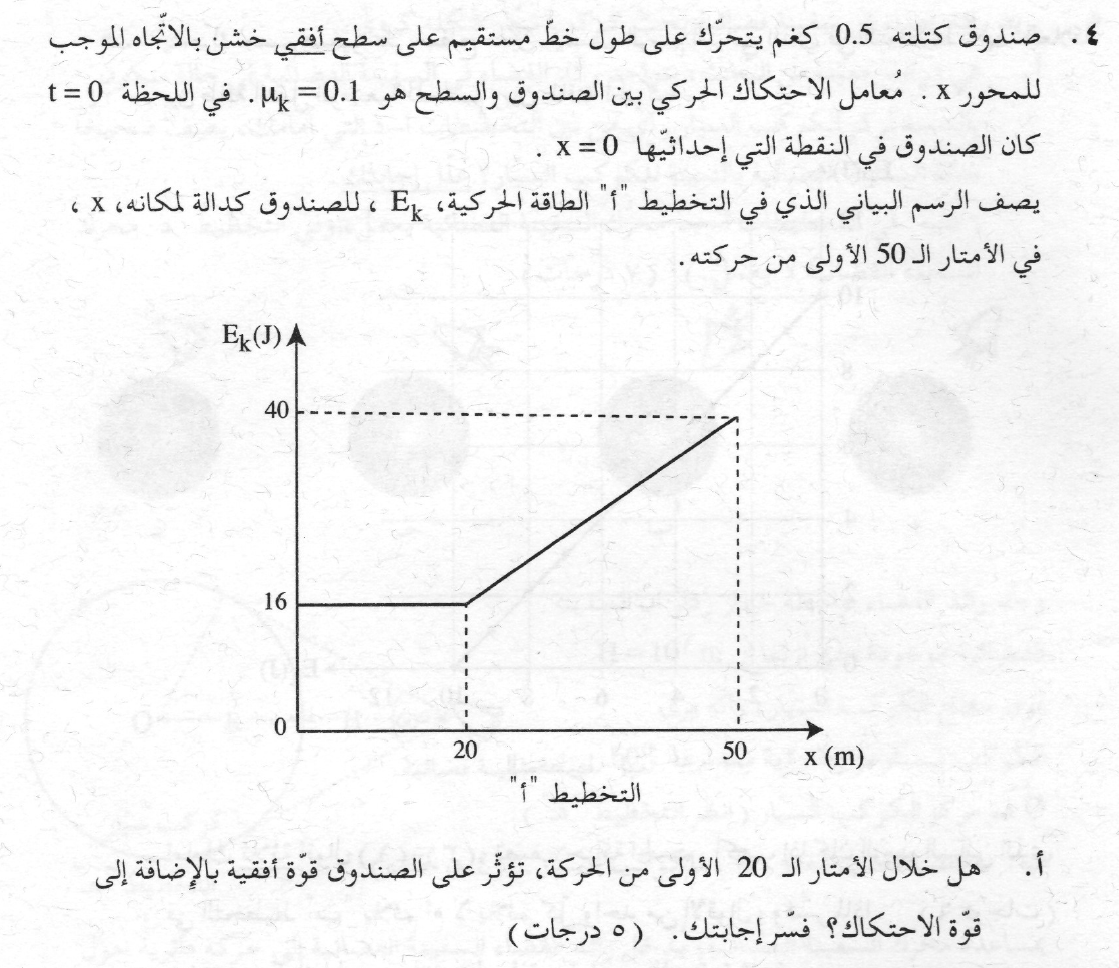
في أول 20 مترًا ، لا تتغير الطاقة الحركية للصندوق، ويتحرك الصندوق بسرعة ثابتة، ويستمر في حركته.
السطح الذي يتحرك عليه الصندوق خشن ، تعمل قوة الاحتكاك ضد اتجاه الحركة.
لكي يستمر الصندوق في التحرك بسرعة ثابتة، على الرغم من قوة الاحتكاك ، يجب أن تعمل قوة إضافية في اتجاه الحركة.

המשטח עליו התיבה נעה הוא מחוספס , פועל כוח חיכוך נגד כיוון התנועה .

כדי שהתיבה תמשיך לנוע במהירות קבועה, למרות כוח החיכוך- חייב לפעול כוח נוסף בכיוון התנועה.

ليس في كل حالة تكون فيها الطاقة الحركية للجسم ثابتة، يكون الجسم مستمرًا في حركته.

يكون الجسم في حالة استمرارية فقط إذا كانت الطاقة الحركية ثابتة، بالإضافة إلى أن الجسم يتحرك في خط مستقيم، كما يظهر في بداية هذا السؤال.

على سبيل المثال، في حركة دائرية منتظمة، تكون الطاقة الحركية ثابتة، لكن الجسم لا يكون في حالة استمرارية.

הגוף מתמיד בתנועתו רק אם האנרגיה הקינטית קבועה ובנוסף הגוף נע בקו ישר, כפי שמופיע בתחילת שאלה זו.

כך לדוגמה בתנועה מעגלית קצובה האנרגיה הקינטית קבועה , אך הגוף לא מתמיד בתנועתו.

______________________________________________________________________________________

...

مقدار القوة F₁ مساوي 1.3 نيوتن.

من نظرية الشغل والطاقة - حسب الازاحة والتغيير في الطاقة الحركية ، يمكن إيجاد محصّلة القوى .
من مبادئ الديناميكا - وفقًا لمحصلة القوى، يمكن ايجاد القوة F₁.

מעקרונות הדינמיקה- בהתאם לכוח השקול ניתן למצוא את הכוח F1.

نفترض أن القوة F₁ تحل محل القوة من القسم "أ" في قسم الحركة هذا. إذن في هذه الثلاثين مترًا فقط قوة الاحتكاك والقوة F₁تعملان.

نجد مقدار القوة المتساوية المؤثرة على الصندوق باستخدام قانون الشغل الطاقة.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«mi mathvariant=¨bold¨»§#931;F«/mi»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«/math»

تعمل محصلة القوى في اتجاه المحور، ويتحرك الجسم في اتجاه المحور، وبالتالي فإن الزاوية α تساوي صفر درجة.

يمكن حساب قيمة التغير في الطاقة الحركية في ثلاثين مترًا من الرسم البياني. والتعبير عن محصلة القوى.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«mi mathvariant=¨bold¨»§#931;F«/mi»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»40«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»16«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»30«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»24«/mn»«mn mathvariant=¨bold¨»30«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/math»

لإيجاد القوة F₁ نرسم مخطط القوى على الصندوق :

نكتب معادلات الحركة ، بالنسبة إلى المحور X الوارد في السؤال والمحور Y ، وهو المحور الرأسي الموجّه لأعلى:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨»y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»F«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«/math»

نعوّض تعبير القوة العمودية من معادلة الحركة العمودية، في تعبير محصلة القوى في معادلة الحركة الأفقية.

نقارن التعبير لمحصلة القوى بقيمة محصلة القوى التي وجدناها من قانون الشغل الطاقة.

ونجد القوة F₁.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mspace linebreak=¨newline¨»«/mspace»«/math»

لذلك، مقدار القوة F₁ مساوي 1.3 نيوتن.

1. في القسم (أ) توصلنا إلى استنتاج مفاده أن قوة أفقية تعمل بالإضافة إلى قوة الاحتكاك. ليس من الواضح ما مصير هذه القوة في القسم ب.

    يمكن افتراض أن هذه القوة تستمر في العمل في القسم ب بالاضافة للقوة F1 ، ويمكن افتراض أن القوة تم استبدالها بـ F1.

    في رأيي، كل حل صحيح يعتمد على أحد هذه الافتراضات يحصل على علامة كاملة.

2. عند استخدام قانون الشغل والطاقة، عندما تعمل عدد من القوى فإن شغل هذه القوى مساوٍ لشغل القوة المحصلة.

    بصيغة أخرى: الشغل في قانون الشغل والطاقة هو مجموع الشغل.

    نظرًا لأننا نبحث عن F₁، فنحن نركز عليها، فهناك ميل خاطئ للاعتقاد بأن الشغل هو فقط للقوة F₁.

3. ميل الرسم البياني بشكل عام يساوي النسبة بين فرق القيم على المحور الرأسي، إلى فرق القيم على المحور الأفقي.

    في الرسم البياني المعطى، يكون الميل هو النسبة بين التغيير في الطاقة الحركية والازاحة. من قانون الشغل والطاقة هذه النسبة تساوي القوة المحصّلة. يمكنك حساب ميل الدالة في الثلاثين مترًا الأخيرة عندها تجد أن قيمة الميل تساوي 0.8 نيوتن.

אפשר להניח שכוח זה ממשיך לפעול בסעיף ב' יחד עם F1 , ואפשר להניח שהכוח מוחלף ע"י F1.

להערכתי כל פתרון נכון , המבוסס על אחת ההנחות האלו יכול לזכות בניקוד מלא.

2. בשימוש במשפט עבודה אנרגיה , כאשר פועלים מספר כוחות העבודה שהיא העבודה של הכוח השקול .

בניסוח אחר: העבודה במשפט העבודה אנרגיה היא של סכום העבודות.

בגלל שאנחנו מחפשים את F1, אנחנו ממוקדים בו, יש נטייה מוטעית לחשוב שהעבודה היא רק של הכוח F1.

______________________________________________________________________________________

...

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»W«/mi»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»65«/mn»«mi mathvariant=¨bold¨»J«/mi»«/math»

من الممكن حساب مقدار قوة الاحتكاك وبالتالي إيجاد شغل قوة الاحتكاك في الخمسين مترًا الأولى - من تعريف الشغل.
يمكن إيجاد شغل قوة الاحتكاك حتى تتوقف الحركة وفقًا لاختلاف الطاقات الحركية - من قانون الشغل والطاقة.

את עבודת כוח החיכוך בהמשך התנועה עד לעצירה , אפשר למצוא בהתאם להפרש האנרגיות הקינטיות- ממשפט העבודה אנרגיה.

افترض أنه بعد توقف عمل القوة F₁. يتحرك الصندوق تحت تأثير قوة الاحتكاك فقط.
يتعلق مقدار قوة الاحتكاك فقط بمعامل الاحتكاك والقوة العمودية، وبالتالي فإن قوة الاحتكاك لا تتغير من اللحظة التي يتحرك فيها الصندوق من مكان x = 0m ، حتى يتوقف الصندوق.

نجد شغل الاحتكاك في مقطعين منفصلين للحركة: المقطع الأول: في أول 50 مترًا ،
والمقطع الثاني يتحرك من المكان x = 50m حتى يتوقف الصندوق.

نجد شغل قوة الاحتكاك في مقطع الحركة الأول في أول 50 مترًا:
نستخدم تعريف الشغل.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«msub»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»x«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»180«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»50«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mspace linebreak=¨newline¨»«/mspace»«/math»

نجد شغل قوة الاحتكاك في مقطع الحركة الثاني:

نستخدم قانون الشغل والطاقة.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/math»

نحسب الشغل الكلي للجاذبية أثناء حركة الصندوق من المكان x = 0m حتى يتوقف الصندوق.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»40«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»65«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/math»

الشغل المبذول بواسطة قوة الاحتكاك هو 65 جول.

גודל כוח החיכוך תלוי רק במקדם החיכוך ובנורמל , לכן כוח החיכוך לא משתנה מרגע שהתיבה נעה ממקום x=0m , ועד שהתיבה נעצרה.

נמצא את עבודת החיכוך בשני קטעי תנועה נפרדים: ב 50 המטרים הראשונים, ובתנועה ממקום x=50m ועד לעצירת התיבה.

נמצא את

إذا استخدمنا قانون الشغل والطاقة في كلا قسمي الحركة في الخمسين مترًا الأولى نجد الشغل للقوة المحصّلة. وليس شغل قوة الاحتكاك. يجب استخدام تعريف الشغل في الخمسين مترًا الأولى. لإيجاد شغل الاحتكاك.

2. أثناء الحركة حتى التوقف، لا نعلم كم الازاحة. لذلك لا يمكن استخدام تعريف الشغل.

تعطى في هذه الحركة الطاقة الحركية الابتدائية، في نهاية الحركة يتوقف الجسم. فقط قوة الاحتكاك هي التي تبذل شغل، لذلك يمكن إيجاد شغل قوة الاحتكاك باستخدام قانون الشغل والطاقة.

3. الشغل عبارة عن كمية قياسية (سكلار)، في حساب الشغل الكلي ، يجب جمع الشغل في جميع أقسام الحركة بشكل قياسي (سكلاري).

4. يكون شغل الاحتكاك سالبًا دائمًا، بغض النظر عن اتجاه الحركة أو التسارع أو اتجاه محور الحركة المحدد.

נמצא את עבודת הכוח השקול. ולא את עבודת כוח החיכוך. בחמישים המטרים הראשונים יש להשתמש בהגדרת העבודה.

למציאת עבודת החיכוך.

2. בתנועה עד לעצירה חסר העתק התנועה . לכן לא ניתן להשתמש בהגדרת העבודה.

נתון בתנועה זו האנרגיה הקינטית ההתחלתית , בסוף התנועה הגוף נעצר. רק כוח החיכוך פועל , לכן ניתן למצוא

את עבודת כוח החיכוך בעזרת משפט העבודה אנרגיה.

3. העבודה הוא גודל סקלרי , בחישוב העבודה הכוללת יש לחבר סקלארית את העבודות בכל קטעי התנועה.

4. עבודת החיכוך היא שלילית תמיד, ללא כל קשר לכיוון התנועה , לתאוצה, או לכיוון ציר התנעה הנבחר.

______________________________________________________________________________________

...

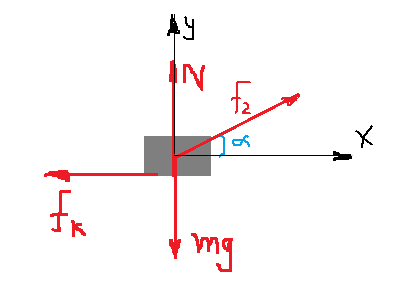
تكون الطاقة الحركية أكبر.

القوة الجديدة لها مركّب في الاتجاه العمودي، فهي تؤثر على القوة العمودية، وبالتالي تؤثر أيضًا على الاحتكاك الحركي.
بحسب التغيير في الاحتكاك الحركي، سيتغير تسارع الصندوق. سوف تتغير سرعته في نهاية الحركة أيضًا.

בהתאם לשינוי בחיכוך הקינטי התאוצה של התיבה תשתנה. גם מהירותה בסוף התנועה תשתנה.

نرسم مخطط القوى في الوضع الجديد، لمقطع الحركة من x = 20m إلى x = 50m.
نقوم بتحليل قائم الزاوية للقوة الجديدة F₂:

نكتب معادلات الحركة في الاتجاهين الأفقي والعمودي:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»F«/mi»«msub»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»F«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«/math»

نعبّر عن التسارع من معادلة الحركة الأفقية:

من معادلة الحركة العمودية، القوة العمودية أصغر. لذلك فإن تسارع الصندوق سيكون أكبر. والسرعة في نهاية هذه الحركة

بدلاً من x = 50m سيكون أكبر. وفقًا لتعريف الطاقة الحركية ، ستكون الطاقة الحركية أكبر.

נכתוב את משוואות התנועה לכיוון האופקי ולכיוון האנכי:

للإجابة على هذا السؤال ، من المهم أن نفهم العلاقة بين العديد من المقادير الفيزيائية

   تؤثر القوة المائلة على القوة العمودية، والقوة العمودية تؤثر على الاحتكاك الحركي، ويؤثر الاحتكاك الحركي على التسارع.

     يؤثر التسارع على السرعة في النهاية، وتحدد السرعة في النهاية الطاقة الحركية.



2. ليس من الممكن أن ندرس من الرسم البياني عن الطاقة الحركية المطلوبة، الرسم البياني يتعامل مع قوة احتكاك مختلفة.

הכוח הנטוי משפיע על הנורמל, הנורמל משפיע על החיכוך הקינטי , החיכוך הקינטי משפיע על התאוצה.

התאוצה משפיעה על המהירות בסוף, והמהירות בסוף בסוף קובעת את האנרגיה הקינטית.

2. לא ניתן ללמוד מהגרף על האנרגיה הקינטית המבוקשת, הגרף עוסק בכוח חיכוך שונה .

______________________________________________________________________________________

...

القول 1- الرسم البياني غير ملائم للقول.
القول 2- الرسم البياني غير ملائم للقول.
القول 3- الرسم البياني ملائم للقول.

היגד 2 - הגרף לא מתאים.

היגד 3- הגרף מתאים.

في الرسم البياني ، تتغير الطاقة الحركية والوضعية بحيث يتم حفظ الطاقة الميكانيكية.

القول 1- الرسم البياني غير ملائم للقول.
تتغير الطاقة الوضعية في الرسم البياني ، بمعنى آخر يتحرك الجسم في نفس الارتفاع.

القول 2- الرسم البياني غير ملائم للقول.
في الرسم البياني ، الخسارة في الطاقة الوضعية يساوي الزيادة في الطاقة الحركية، الطاقة الميكانيكية تُحفظ
هنالك قوة احتكاك تبذل شغل، ولا يتم حفظ الطاقة الميكانيكية.

القول 3- الرسم البياني ملائم للقول.
في الرسم البياني يتم حفظ الطاقة الميكانيكية.
يتحرك الجسم تحت تأثير قوة الجاذبية فقط ، وبالتالي تُحفظ الطاقة الميكانيكية.

الرسم البياني لا يتناول المكان والزمان. من الخطأ القول إن الطاقة الوضعية في البداية كانت 10 جول.

    من الصحيح فقط القول أنه عندما كانت الطاقة الوضعية 10 جول كانت الطاقة الحركية صفر جول.

    يمكن للرسم البياني أن يلائم أي حركة حيث فقط قوة الجاذبية تعمل شغل. يمكن أن تكون أي حركة باليستية. حركة البندول ، الحركة على سكة عمودية. .

2. انتبه إلى شكل الدالة في الرسم البياني، والقيم الموجودة في الرسم البياني، ولاحظ أن الطاقة الميكانيكية تُحفظ.

3. في الفقرة التمهيدية من هذا القسم، تمت كتابة أن الجسم يتحرك على سطح ما ، وأي جسم يتحرك على سطح لا يتحرك في حالة السقوط الحر.

    السقوط الحر هو حركة تحت تأثير الجاذبية فقط ، تؤثر القوة العمودية على الجسم في هذه الحالة.

    ومع ذلك ، فإن العبارة الثالثة صحيحة ، لأنها تناسب الرسم البياني ، (على الرغم من أنها لا تناسب الفقرة التمهيدية)

נכון לומר רק שכאשר האנרגיה הפוטנציאלית הייתה 10 ג'אול האנרגיה הקינטית הייתה אפס ג'אול.

הגרף יכול להתאים לכל תנועה שבה רק כוח הכובד עושה עבודה. זה יכול להיות כל תנועה בליסטית.

תנועת מטוטלת , תנועה במסילה אנכית . ועוד.

2. רבים וטובים , יראו גרף זה ויחשבו קצת לפני שיתחילו להבין מה הולך כאן, יש שאלות כאלו, הן מעולות ונדירות.

3. יש לשים לב לצורת הפונקציה בגרף, ולערכים בגרף, ולהבחין בעובדה החשובה - האנרגיה המכנית נשמרת.

4. בפסקת המבוא של סעיף זה כתוב שהגוף נע על משטח , כל גוף הנע על משטח לא נע בנפילה חופשית.

נפילה חופשית היא תנועה בהשפעת כוח הכבידה בלבד , על הגוף במקרה זה פועל כוח הנורמל.

ובכל זאת ההיגד השלישי נכון , מכיוון שהוא מתאים לגרף, (למרות שהוא לא מתאים לפסקת המבוא)

______________________________________________________________________________________