______________________________________________________________________________________
...
تتغير السرعة في الاتجاه ، لذلك هناك تسارع.
تعريف التسارع.
تتحرك منظومة "الكرسي والطفل" بسرعة متغيرة الاتجاه ، لذلك من تعريف التسارع فإن تسارع المنظومة لا يساوي صفر.
يتم تعريف التسارع على أنه وتيرة تغيّر السرعة ، إذا تغيرت السرعة فقط في المقدار أو في الاتجاه فقط هناك تسارع.
إذا استخدمنا تعريف التسارع لحالة الحركة الدائرية المنتظمة، فسنحصل على متجه موجّه نحو نقطة مركز الدوران.
لذلك ، في حركة دائرية منتظمة هناك تسارع نحو مركز الدوران.
אם נשתמש בהגדרת התאוצה למקרה של תנועה מעגלית קצובה נקבל ווקטור שכיוונו אל נקודת מרכז הסיבוב.
לכן ,בתנועה מעגלית קצובה יש תאוצה רדיאלית.
______________________________________________________________________________________
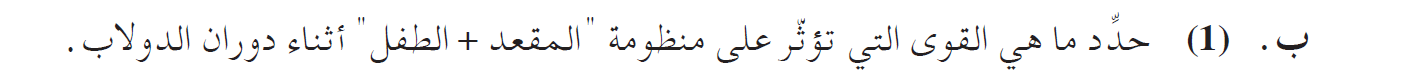
______________________________________________________________________________________
...
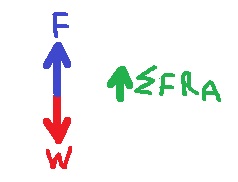
بإهمال قوة الاحتكاك ، القوى هي: قوة الجاذبية -W. القوة التي يشغّلها الدولاب الضخم - F.
تعمل القوة بين الاجسام، من أجل تحديد من هي القوى العاملة ، يجب أن فهم من هي الأجسام التي تؤثر على الحركة.
بإهمال قوة الاحتكاك ، القوى هي: قوة الجاذبية -W. القوة التي يشغّلها الدولاب الضخم - F.
تتعلق قوة الاحتكاك مع الهواء على سرعة الجسم في الهواء. في هذه الحالة تكمل الدولاب دورة لمدة 20 دقيقة ، وسرعتها صغيرة. قوة الاحتكاك مع الهواء مهملة.
______________________________________________________________________________________
ب.

______________________________________________________________________________________
...
في حركة دائرية منتظمة، يجب أن تكون محصلة القوى (لجميع القوى المؤثرة) ثابتة المقدار وتعمل باتجاه نقطة مركز الدوران.
بإهمال قوة الاحتكاك ، تعمل قوتان على المنظومة "الكرسي + الطفل" ، قوة الجاذبية W ، والقوة التي يشغّلها الدولاب F.
تتحرك المنظومة في حركة دائرية منتظمة، وبالتالي فإن القوة المحصّلة لقوة الجاذبية والقوة F هي القوة الجاذبة نحو المركز وهي ثابتة المقدار.
ويتحقق: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#931;F«/mi»«mi mathvariant=¨bold¨»R«/mi»«/msub»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»W«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/math» لذلك فإن تعبير القوة التي يشغّلها الدولاب في أي لحظة هو: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mover mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#931;F«/mi»«mi mathvariant=¨bold¨»R«/mi»«/msub»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»W«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/math»
قوة الجاذبية ثابتة في مقدارها واتجاهها ، ومقدارها يساوي وزن الجسم واتجاهها نحو الأسفل.
اتجاه قوة الجاذبة نحو نقطة مركز الدوران. قبل تحديد اتجاه القوة F ، نجد مقدار قوة الجاذبة: نحو مركز الدوران
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#931;F«/mi»«mi mathvariant=¨bold¨»R«/mi»«/msub»«mrow»«/mrow»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»120«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mfenced mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»60«/mn»«/mrow»«/mfrac»«/mfenced»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»60«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7200«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«msup»«mn mathvariant=¨bold¨»1200«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»284«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»244«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»440«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»000«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»197«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/math»
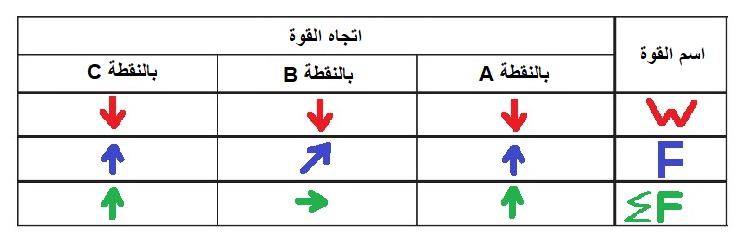
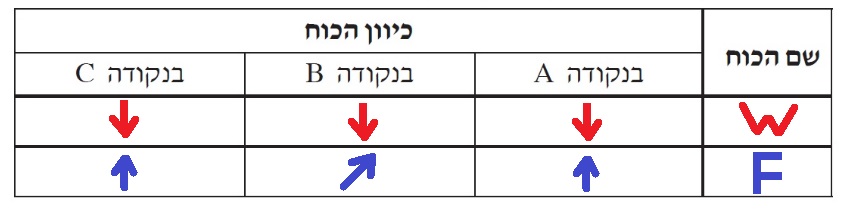
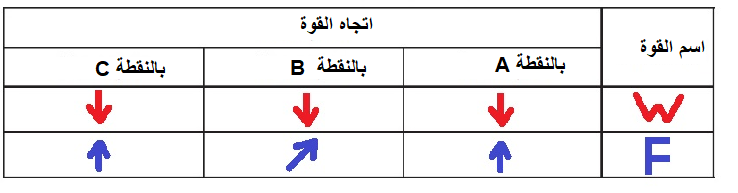
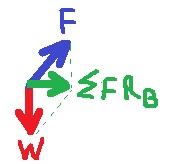
في النقطة (أ): تعمل قوة الجاذبية لأسفل، بحيث تكون هناك قوة محصّلة مقدارها 0.197 نيوتن باتجاه مركز الدوران.
يجب أن يشغّل الدولاب قوة نحو الأعلى في هذه النقطة.
בנקודה B:
في النقطة B: نظرًا لأن قوة الجاذبية تعمل لأسفل ، يجب أن تعمل القوة التي يشغّلها الدولاب لأعلى مع ميل إلى اليمين
بحيث تكون المحصلة مساوية للقوة الجاذبة نحو المركز.
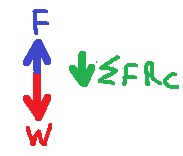
في النقطة C: في هذه النقطة ، تعمل القوة الجاذبة نحو المركز للأسفل ، ولكن نظرًا لأن قوة الجاذبة المركزية أصغر بكثير من وزن المنظومة
يجب أن على الدولاب أن يُشغّل قوة لأعلى.
نكمل الجدول:
המערכת נעה בתנועה מעגלית קצובה , לכן הכוח השקול לכוח הכובד ולכוח F הוא כוח צנטריפטלי הקבוע בגודלו.
ומתקיים: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#931;F«/mi»«mi mathvariant=¨bold¨»R«/mi»«/msub»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»W«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/math» לכן ביטוי הכוח שהגלגל מפעיל בכל רגע הוא: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mover mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#931;F«/mi»«mi mathvariant=¨bold¨»R«/mi»«/msub»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»W«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/math»
כוח הכובד קבוע בגודלו ובכיוונו , גודלו כמשקל הגוף וכיוונו למטה.
כיוונו של הכוח הצנטריפטאלי הוא אל נקודת מרכז הסיבוב . לפני קביעת כיוונו של הכוח F , נמצא את גודלו של הכוח הצנטריפטלי:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#931;F«/mi»«mi mathvariant=¨bold¨»R«/mi»«/msub»«mrow»«/mrow»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»120«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mfenced mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»60«/mn»«/mrow»«/mfrac»«/mfenced»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»60«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7200«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«msup»«mn mathvariant=¨bold¨»1200«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»284«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»244«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»440«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»000«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»197«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/math»
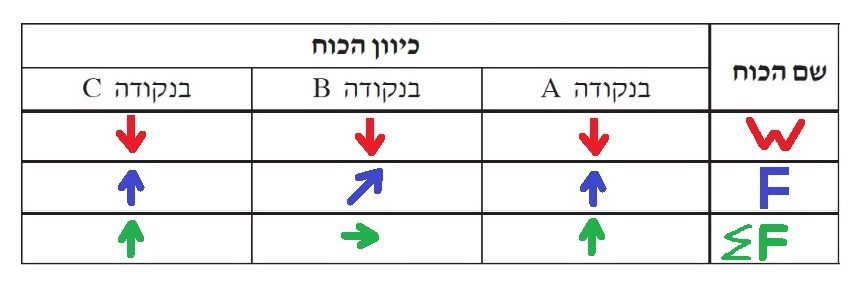
בנקודה A: כוח הכובד פועל כלפי מטה , כדי שיהיה כוח שקול שגודלו 0.197 ניוטון כלפי מרכז סיבוב.
הגלגל חייב להפעיל בנקודה זו כוח כלפי מעלה.
בנקודה B: בגלל שכוח הכובד פועל כלפי מטה הכוח שהגלגל מפעיל צריך לפעול כלפי מעלה עם נטייה לימין
כך שהשקול יהיה הכוח הצנטריפטאלי.
בנקודה C: בנקודה זו הכוח הצנטריפטלי פועל כלפי מטה , אך מכיוון שהכוח הצנטריפטלי קטן בהרבה ממשקל המערכת
הכוח שהגלגל צריך להפעיל חייב לפעול כלפי מעלה .
נשלים את הטבלה:
1.
ليس من الممكن تحديد اتجاه القوة F في النقطة C دون معرفة مقدار القوة الجاذبة نحو المركز.
إذا كانت القوة الجاذبة نحو المركز أكبر من قوة الجاذبية - يكون اتجاه
القوة F لأسفل.
إذا كانت القوة الجاذبة نحو المركز أقل من قوة الجاذبية - يكون اتجاه القوة
F لأعلى.
2. يتحرك الدولاب
في حركة دائرية ثابتة - وهي حركة تبدو بسيطة. لكن لأن قوة الجاذبية ثابتة المقدار
والاتجاه والقوة الجاذبة نحو المركز يجب أن تعمل في
كل لحظة نحو مركز الدوران ولا يتغير مقدارها (حركة دائرية ثابتة) لذلك، فإن القوة التي يشغّلها الدولاب في كل
نقطة يجب أن تلائم نفسها بحيث تكون محصلة القوى تكون مساوية للقوة الجاذبة نحو
المركز المطلوبة.
في كل نقطة، يُشغّل
الدولاب على المنظومة قوة مختلفة من حيث المقدار والاتجاه.
لفهم هذا
جيدًا ، دعنا نفكر في منظومة مماثلة موصلة بواسطة خيط بالدولاب الضخم، لنفرض أن
مسمارًا مغروزًا في الخيط.
في كل نقطة،
سيؤثر الخيط قوة مختلفة على المسمار، كما سيؤثر المسمار أيضًا بقوة مختلفة على الخيط القوة التي يشغّلها المسمار على السلك هي
القوة F.
3. معطى في السؤال قطر الدولاب، فيجب استخدام نصف القطر
في حساب القوة الجاذبة نحو المركز.
4. يجب تحويل زمن حركة الدولاب إلى ثوان.
5. أيضًا في النقطة A والنقطة C ، تعمل
القوة F
لأعلى ، في النقطة A تكون قيمة F أكبر.
אם הכוח הצנטריטלי גדול מכוח הכובד- כיוון הכוח F הוא כלפי מטה.
אם הכוח הצנטריטלי קטן מכוח הכובד- כיוון הכוח F הוא כלפי מעלה.
2. הגלגל נע בתנועה מעגלית קצובה - תנועה לכאורה פשוטה . אך מכיוון שכוח הכובד קבוע בגודלו ובכיוונו
והכוח הצנטריפטאלי חייב לפעול בכל רגע לנקודת מרכז הסיבוב וגודלו לא משתנה (תנועה מעגלית קצובה)
לכן הכוח שהגלגל מפעיל בכל נקודה צריך להתאים את עצמו כך ששקול הכוחות שלו ושל כוח הכובד
יהיה הכוח הצנטריפטלי הדרוש.
בכל נקודה הגלגל מפעיל על המערכת כוח שונה בגודלו ובכיוונו.
כדי להבין זאת בצורה טובה , נחשוב על מערכת זהה מחוברת בעזרת חוט לגלגל הענק , נניח שבחוט נעוץ מסמר.
בכל נקודה החוט יפעיל כוח שונה על המסמר, וגם המסמר יפעיל כוח שונה על החוט.
הכוח שהמסמר מפעיל על החוט הוא הכוח F.
3. בשאלה נתון קוטר הגלגל , בחישוב הכוח הצנטריפטלי יש להשתמש ברדיוס.
4. את זמן תנועת הגלגל יש להמיר לשניות.
5. גם בנקודה A ובנקודה C פועל כוח F כלפי מעלה , בנקודה A ערכו של F גדול יותר.
______________________________________________________________________________________
ب.
 ____________________________________________________________________________________
____________________________________________________________________________________
...
في أي حركة دائرية منتظمة، محصلة القوى هي القوة الجاذبة نحو المركز.
تتحرك المنظومة مع الدولاب في حركة دائرية منتظمة، في كل حركة دائرية منتظمة، تكون محصلة القوى هي القوة الجاذبة نحو المركز، قوة مقدارها ثابت تعمل باتجاه مركز الدوران.
لا يمكن الإجابة على القسم 2 دون فهم القسم 3. بالنسبة للجزء الأكبر ، عادة يأخذ ترتيب الأقسام في الأسئلة الطالب في الاعتبار ، ويبني الفهم بطريقة جيدة.
______________________________________________________________________________________

______________________________________________________________________________________
...
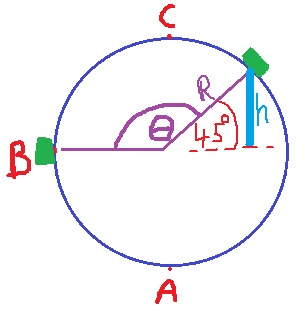
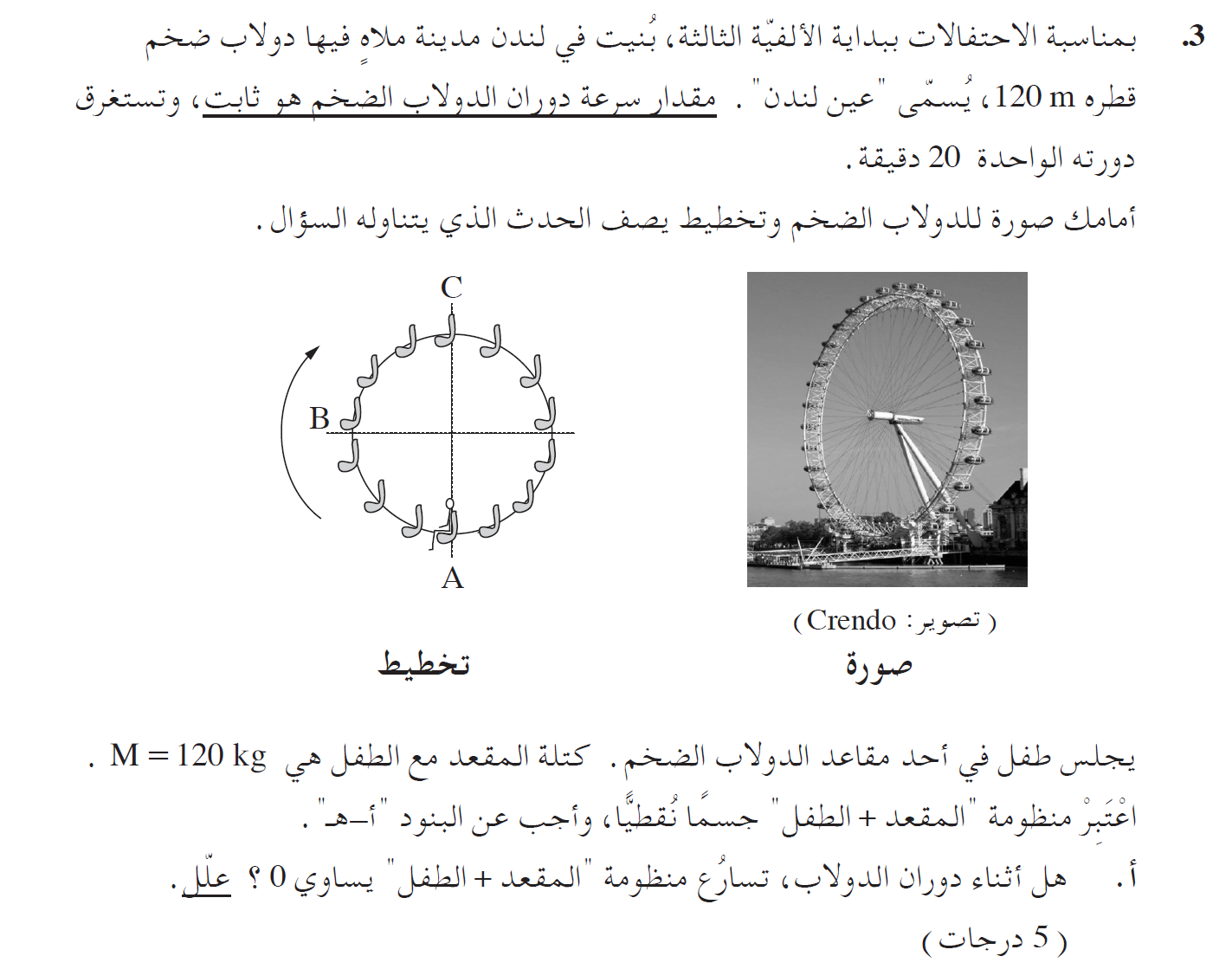
تحديد محور الحركة الرأسية ووصف موقع المنظومة نسبة للمحور أثناء زمن الدورة الكاملة.
نصف الموقع الرأسي كدالة للزمن نسبة لمحور الحركة العمودية الذي نقطة أصله في النقطة B.
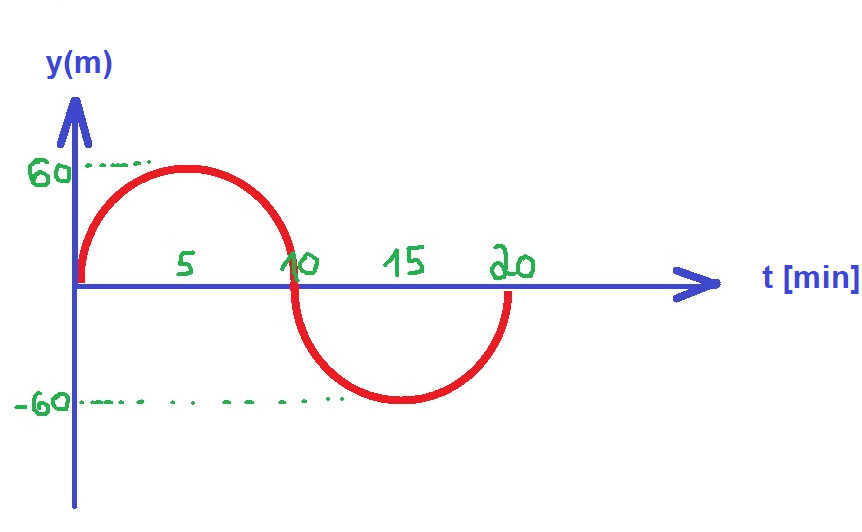
نسبة للمحور المحدّد في دورة كاملة، تبدأ المنظومة في التحرك من الموقع صفر إلى الموقع 60 مترًا ، ومن هناك تنزل المنظومة إلى موقع أقل من 60 مترًا ، وفي نهاية الحركة تعود المنظومة إلى موقع النقطة B.
نرسم رسم بياني يصف الموقع الرأسي كدالة للزمن:
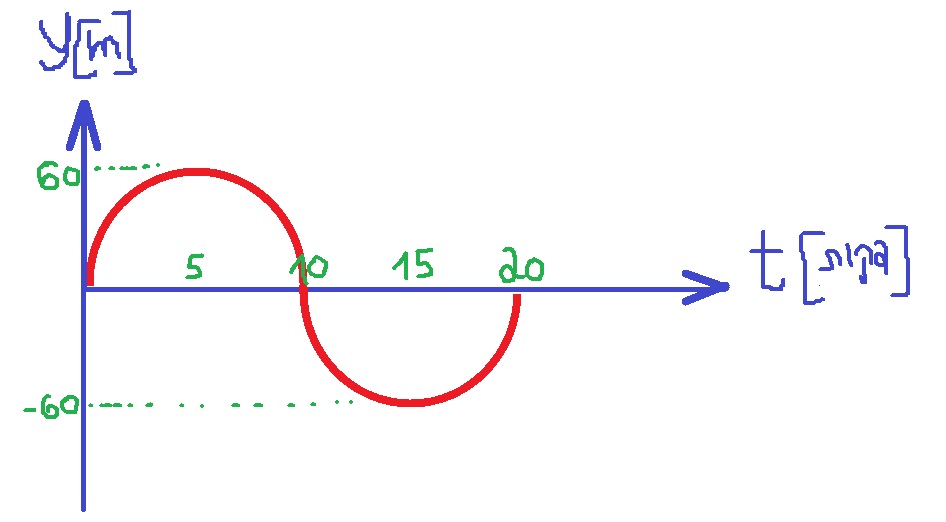
ביחס לציר הנבחר בסיבוב שלם המערכת מתחילה לנוע ממיקום אפס ,למיקום 60 מטר , ומשם המערכת יורדת למיקום מינוס 60 מטר , ובסוף התנועה חוזרת המערכת למיקום הנקודה B.
נערוך גרף המתאר את המיקום האנכי בתלות בזמן:
1. تتحرك المنظومة في
حركة دائرية منتظمة، في الاتجاه العمودي (وأيضًا أفقيًا) تتحرك المنظومة بسرعة
متغيرة.
في النقطة B تكون السرعة
العمودية قصوى. وفي النقطة C ، تكون السرعة العمودية صفرًا.
تتغير السرعة العمودية، وبالتالي في الرسم
البياني للمكان كدالة للزمن سيتغير ميل الرسم البياني وفقًا لذلك.
2. إذا علّمنا موقع
المنظومة كل فترة زمنية ثابتة، فسنحصل على مخطط تتبع لمسار المنظومة.
في نصف زمن الدورة الأولى ، يكون شكل المسار
شبيه للرسم البياني للموقع العمودي كدالة للزمن.
בנקודה B המהירות האנכית מקסימאלית. ובנקודה C המהירות האנכית היא אפס.
המהירות האנכית משתנה, לכן בגרף מקום בתלות בזמן השיפוע של הגרף משתנה בהתאם.
2. אם נסמן את מיקום המערכת כל פרק זמן קבוע , נקבל תרשים עקבות של מסלול תנועת המערכת.
בחצי זמן המחזור הראשון צורת המסלול זהה לגרף המקום האנכי בתלות בזמן .
______________________________________________________________________________________

______________________________________________________________________________________
...
التغيير في الطاقة الميكانيكية يساوي 50911.68 جول.
لا تتغير الطاقة الحركية ، فقط الطاقة الوضعية تتغير وفقًا للارتفاع الذي تصل إليه المنظومة.
حسب زمن الحركة 0.375T ، يمكنك ايجاد مقدار التغيير في الزاوية المركزية واعتمادًا على الشكل الهندسي ، يمكنك ايجاد ارتفاع المنظومة.
والتغيّر في الطاقة الوضعية.
בהתאם לזמן התנועה 0.375T ניתן למצוא את גודל השינוי בזווית המרכזית ובהתאם גיאומטרית ניתן למצוא את גובה המערכת .
והשינוי באנרגיה הפוטנציאלית .
الطاقة الميكانيكية تساوي مجموع الطاقة الحركية والطاقة الوضعية.
يتحرك النظام في حركة دائرية منتظمة، وبالتالي لا يوجد تغيير في الطاقة الحركية.
يتغير الموقع الرأسي للمنظومة، وبالتالي هناك تغيير في الطاقة الوضعية.
نستخدم تعريف السرعة الزاوية ونحسب التغيير في الزاوية المركزية خلال مدة 0.375T ثانية.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»§#952;«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»375«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»360«/mn»«mo mathvariant=¨bold¨»§#176;«/mo»«/mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»375«/mn»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»135«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#176;«/mo»«mspace linebreak=¨newline¨»«/mspace»«/math» 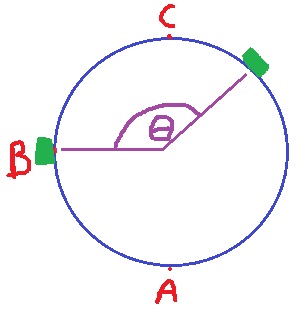
نحدد مستوى انتساب في ارتفاع النقطة B ونجد ارتفاع الجسم h بعد 0.375T ثانية.
نستعمل نسبة sin:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»60«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»45«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»42«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»42«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨»«/mspace»«/math»
نحسب تغيير الطاقة الميكانيكية والتي تساوي التغير في الطاقة الوضعية بعد 0.375T ثانية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»120«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»42«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»42«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»50«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»911«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»68«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/math»
لذلك ، فإن التغير في الطاقة الميكانيكية يساوي 50911.68 جول.
המערכת נעה בתנועה מעגלית קצובה , לכן אין שינוי באנרגיה הקינטית.
המיקום האנכי של המערכת משתנה , לכן יש שינוי באנרגיה הפוטנציאלית .
נשתמש בהגדרת המהירות הזוויתית ,ונחשב את השינוי בזווית המרכזית במשך 0.375T שניות.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»§#952;«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»375«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»360«/mn»«mo mathvariant=¨bold¨»§#176;«/mo»«/mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»375«/mn»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»135«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#176;«/mo»«mspace linebreak=¨newline¨»«/mspace»«/math» 
נגדיר מישור ייחוס בגובה הנקודה B .ונמצא את הגובה של הגוף h כעבור 0.375T שניות.
נשתמש בזהות הסינוס:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»60«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»45«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»42«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»42«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨»«/mspace»«/math»
נחשב את האנרגיה השינוי באנרגיה הפוטנציאלית במשך כעבור 0.375T שניות :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»120«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»42«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»42«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»50«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»911«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»68«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/math»
العلاقة بين زمن الحركة والتغير في الارتفاع ليست مفهومة ظمنًا، يجب رسم مخطط باستخدام مبادئ الحركة الدائرية.
وإعطاء بعض الوقت للتفكير في مسار الحل.
ולתת קצת זמן לחשיבה על מהלך הפתרון.
______________________________________________________________________________________

______________________________________________________________________________________
...
الشغل الكلي هو صفر لأنه لا يوجد تغيير في الطاقة الحركية.
قانون الشغل والطاقة.
يتحرك الجسم في حركة دائرية منتظمة، وبالتالي لا يوجد تغيير في الطاقة الحركية. من قانون الشغل والطاقة ، «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«/math» نظرًا لعدم وجود تغيير في الطاقة الحركية ، فإن الشغل الكلي يساوي صفرًا.
لكي
تكون قادرًا على الإجابة على هذا القسم بشكل صحيح، يجب عليك فهم تعريف الشغل الكلي
مفهومًا جيدًا. وتمييزه عن الطاقة الميكانيكية الكلية.
الشغل الكلي يعني مجموع شغل كل القوى المؤثرة
على الجسم - بما في ذلك شغل قوة الجاذبية!
2. لفهم الفرق بين الأمرين
جيدًا، تحتاج إلى فهم كيفية نشوء الطاقة الميكانيكية:
ولدت
فكرة الطاقة الميكانيكية من قانون الشغل والطاقة، عندما يُبذل شغل بواسطة قوة
حافظة.
في
مثل هذه الحالة يوصف شغل القوة الحافظة ناقص التغيّر في الطاقة الوضعية
لتلك القوة الحافظة.
بعد
نقل التغيير في الطاقة الوضعية إلى الطرف الآخر للمعادلة، يتم الحصول على تعبير
مفاده أن هناك شغلًا في طرف واحد وفي الطرف الآخر مجموع تغيير الطاقة: التغيير في
الطاقة الحركية والتغير في الطاقة الكامنة. هذا يسمى تغيير الطاقة الميكانيكية
باختصار.
رياضيا
يبدو كالتالي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨16px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#931;W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1581;§#1601;§#1592;§#1577;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1594;§#1610;§#1585;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1602;§#1608;§#1609;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1588;§#1594;§#1604;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mprescripts/»«mrow mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1580;§#1575;§#1584;§#1576;§#1610;§#1577;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1602;§#1608;§#1577;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1588;§#1594;§#1604;«/mi»«/mrow»«none/»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#7F007F¨ notation=¨box¨»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1580;§#1575;§#1584;§#1576;§#1610;§#1577;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1602;§#1608;§#1577;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1588;§#1594;§#1604;«/mi»«mi mathvariant=¨bold¨»W«/mi»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»U«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1575;§#1604;§#1581;§#1575;§#1601;§#1592;§#1577;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1575;§#1604;§#1594;§#1610;§#1585;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1575;§#1604;§#1602;§#1608;§#1609;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1588;§#1594;§#1604;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#7F007F¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#7F007F¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#7F007F¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1575;§#1604;§#1581;§#1575;§#1601;§#1592;§#1577;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1575;§#1604;§#1594;§#1610;§#1585;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1575;§#1604;§#1602;§#1608;§#1609;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1588;§#1594;§#1604;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#FF0000¨ notation=¨box¨»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1581;§#1575;§#1601;§#1592;§#1577;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1594;§#1610;§#1585;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1602;§#1608;§#1609;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1588;§#1594;§#1604;«/mi»«mi mathvariant=¨bold¨»W«/mi»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«munder»«munder»«mfenced»«mrow»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»U«/mi»«/mrow»«/mfenced»«mo mathvariant=¨bold¨»§#9183;«/mo»«/munder»«mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1605;§#1610;§#1603;§#1575;§#1606;§#1610;§#1603;§#1610;§#1577;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1591;§#1575;§#1602;§#1577;«/mi»«/mrow»«/munder»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
إذا
كانت القوة الحافظة هي التي تبذل شغل فقط ... فإن التغير في الطاقة الميكانيكية يساوي
صفرًا. إذا قلّت الطاقة الحركية، تزداد الطاقة الوضعية بحيث لا يتغير مجموعهما ،
وهذا هو مبدأ حفظ الطاقة الميكانيكية.
3. في هذه الحالة يكون شغل
القوة غير الحافظة هو شغل الدولاب الضخم.
4. حسب حركة المنظومة وتعريف
الشغل فإن شغل قوة الجاذبية في هذه الحالة يكون سالبًا. وشغل الدولاب الضخم يكون بنفس
المقدار لكنه موجب. (قوة الجاذبية تعيق الدولاب في تحريك المنظومة)، لأن القيمة
المطلقة لشغل كل منهما متساوٍ يكون الشغل الكلي يساوي صفر، لا يوجد تغيير في
الطاقة الحركية.
5. موضوع الطاقة سهل التنفيذ
للغاية، وليس من السهل فهمه، حتى نيوتن لم تخطر على باله الفكرة. لفهم جميع
المفاهيم تمامًا، حاول أن تشرح لنفسك ثم قم بربط العملية برمتها: قانون الشغل والطاقة -> الطاقة الوضعية -> الطاقة الميكانيكية
-> حفظ الطاقة الميكانيكية.
في
كل مرة تتعثر فيها، لا تستسلم، ارجع قليلاً، واستمر حتى تصل إلى النهاية.
حتى
لو مرت بضعة أيام أو أشهر ، ووجدت صعوبة في إكمال العملية، عندما تحصل على أسئلة
حول ماهية الطاقة الكلية وما هو التغيير في الطاقة الميكانيكية ، ستعرف كيف تميز
بين الاثنين.
6. لمساعدة الطالب على التمييز
بين الشغل الكلي وشغل القوى غير الحافظة، تظهر على صفحات الصيغ (ورقة القوانين)
تعبيرات هذين الشغلين:
עבודה כוללת משמעותה סכום כל העבודות של כל הכוחות הפועלים על הגוף- כולל עבודת כוח הכובד!
2. כדי להבין ממש טוב את ההבדל בין שני הדברים צריך להבין כיצד נולדה האנרגיה המכנית:
רעיון האנרגיה המכנית נולד ממשפט העבודה אנרגיה , כאשר מבוצעת עבודה של כוח משמר.
במקרה כזה מתוארת עבודת הכוח המשמר כמינוס השינוי באנרגיה הפוטנציאלית של אותו כוח משמר.
לאחר העברת השינוי באנרגיה הפוטנציאלית אגף, מתקבל ביטוי שבצידו האחד יש עבודה ובצידו השני סכום של שינוי אנרגיות: השינוי באנרגיה הקינטית והשינוי באנרגיה הפוטנציאלית. לזה קוראים בקיצור שינוי האנרגיה המכנית.
מתמטית זה נראה כך:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#931;W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mprescripts»«/mprescripts»«mrow mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»§#1502;§#1513;§#1502;§#1512;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1500;§#1488;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1499;§#1493;§#1495;«/mi»«/mrow»«none»«/none»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mprescripts»«/mprescripts»«mrow mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»§#1492;§#1499;§#1493;§#1489;§#1491;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1499;§#1493;§#1495;«/mi»«/mrow»«none»«/none»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#7F007F¨ notation=¨box¨»«mmultiscripts»«mi mathvariant=¨bold¨»W«/mi»«mprescripts»«/mprescripts»«mrow»«mi mathvariant=¨bold¨»§#1492;§#1499;§#1493;§#1489;§#1491;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1499;§#1493;§#1495;«/mi»«/mrow»«none»«/none»«/mmultiscripts»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»U«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mprescripts»«/mprescripts»«mrow mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»§#1502;§#1513;§#1502;§#1512;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1500;§#1488;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1499;§#1493;§#1495;«/mi»«/mrow»«none»«/none»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#7F007F¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#7F007F¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#7F007F¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mprescripts»«/mprescripts»«mrow mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»§#1502;§#1513;§#1502;§#1512;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1500;§#1488;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1499;§#1493;§#1495;«/mi»«/mrow»«none»«/none»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#FF0000¨ notation=¨box¨»«mmultiscripts»«mi mathvariant=¨bold¨»W«/mi»«mprescripts»«/mprescripts»«mrow»«mi mathvariant=¨bold¨»§#1502;§#1513;§#1502;§#1512;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1500;§#1488;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1499;§#1493;§#1495;«/mi»«/mrow»«none»«/none»«/mmultiscripts»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«munder»«munder»«mfenced»«mrow»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»U«/mi»«/mrow»«/mfenced»«mo mathvariant=¨bold¨»§#9183;«/mo»«/munder»«mrow»«mi mathvariant=¨bold¨»§#1502;§#1499;§#1504;§#1497;§#1514;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1488;§#1504;§#1512;§#1490;§#1497;§#1492;«/mi»«/mrow»«/munder»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
אם רק כוח משמר עושה עבודה .... השינוי באנרגיה המכנית הוא אפס. אם הקינטית קטנה הפוטנציאלית גדלה כך שסכומם לא משתנה , וזה שימור האנרגיה המכנית.
3. במקרה זה עבודת הכוח לא משמר היא עבודת הגלגל ענק.
4. בהתאם לתנועת המערכת ולהגדרת העבודה , עבודת כוח הכובד בנקרה זה היא שלילית. ועבודת הגלגל הענק היא זהה בגודלה , אך היא חיובית. (כוח הכובד "מפריע" לגלגל להניע את המערכת) , בגלל שבערך המוחלט העבודות זהות העבודה הכוללת שווה לאפס, אין שינוי באנרגיה הקינטית.
5. נושא האנרגיה קל לביצוע מאוד לא קל להבנה , גם לא ניוטון לא עלה על הרעיון. כדי להבין היטב את כל המושגים, נסו להסביר לעצמכם ואח"כ לחבר את כל המהלך: משפט עבודה אנרגיה -> אנרגיה פוטנציאלית-> אנרגיה מכנית-> שימור אנרגיה מכנית.
בכל פעם שתתקעו , אל תתייאשו תחזר קצת , ותמשיכו קדימה עד שתגיעו לסוף.
גם אם כאשר יעברו כמה ימים או חודשים , ותתקשו להשלים את המהלך , כשתקבלו שאלות עם מה האנרגיה הכוללת ומה השינוי באנרגיה המכנית , תדעו להבחין בין השניים.
6. כדי לעזור לתלמיד להבחין בין עבודה הכוללת לעבודת הכוחות הלא משמרים, בדפי הנוסחאות מופיעים הביטויים של שני עבודות אלו :
______________________________________________________________________________________

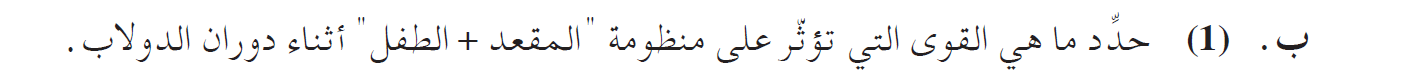






 ____________________________________________________________________________________
____________________________________________________________________________________