______________________________________________________________________________________
...
في النقطتين 1 و 5 يكون التسارع المماسي ذو قيمة قصوى.
من المهم أن نفهم من هي القوة التي تسبب التسارع المماسي، وأن ترسم مخططًا للقوى وتكتب معادلة الحركة في الاتجاه المماسي.
لفهم في أي نقطة يكون فيها التسارع المماسي أقصى مقدار له، تم تطوير تعبير للتسارع المماسي، كدالة لزاوية ميل الخيط.
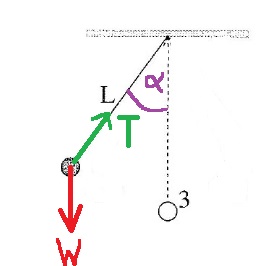
نشير إلى هذه الزاوية بواسطة α.
نرسم مخطّط قوى:
تعمل قوة الشد في الاتجاه المركزي (راديالي) ، وليس لها أي مركّب في الاتجاه المماسي للحركة.
ينتج التسارع المماسي من مركّب الجاذبية في الاتجاه المماسي.
سنقوم بتحليل قائم الزاوية لقوة الجاذبية، في اتجاه المماس WX وفي الاتجاه المعاكس لقوة الشد WY.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»mg«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»mg«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math»
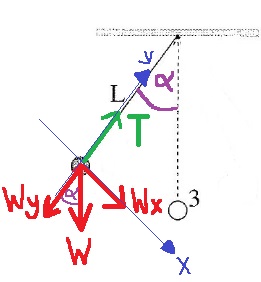
مركّب قوة الجاذبية WX هو القوة المماسية، والتي تسبب التسارع المماسي.
نكتب معادلة الحركة في الاتجاه المماسي، ونعبر منه عن التسارع المماسي :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/math»
من التعبير عن التسارع المماسي ، يمكن ملاحظة أنه كلما زادت زاوية ميل الخيط، زاد التسارع المماسي.
نظرًا لأن الاحتكاك مهمل في النقطتين 1 و 5 ، فإن زاوية ميل الخيط هي نفسها ، وعند هذه النقاط تكون زاوية ميل الخيط بحد أقصى.
لذلك في النقطتين 1 و 5 يكون أقصى تسارع مماسي.
נסמן זווית זאת ע"י α .
נערוך תרשים כוחות:
כוח המתיחות פועל בכיוון הרדיאלי , אין לו רכיב בכיוון משיק לתנועה.
התאוצה המשיקית נוצרת מרכיב כוח הכובד בכיוון המשיקי.
נבצע הפרדה ישרת זווית לכוח הכובד , לכיוון המשיקי WX ולכיוון הנגדי למתיחות WY.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»mg«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»mg«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math»

רכיב כוח הכובד WX הוא הכוח המשיקי , הגורם לתאוצה המשיקית .
נכתוב את משוואת התנועה לכיוון המשיקי , ונבטא ממנה את התאוצה המשיקית:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/math»
מביטוי התאוצה המשיקית , ניתן לראות שככל שזווית נטיית החוט גדולה יותר התאוצה המשיקית גדולה יותר.
1. يمكن للجسم أن يتحرك بسرعة صغيرة وبتسارع كبير، ويمكنه أن يتحرك بسرعة هائلة بدون تسارع.
لا تشير السرعة إلى مقدار التسارع.
من خلال هذا السؤال ، من الممكن تقدير مكان السرعة الكبيرة وحيث تكون السرعة صغيرة ، ومن هذا وحده لا يمكن التعرف على التسارع المماسي.
2. يجب تحليل قائم الزاوية لقوة الجاذبية وليس لقوة التوتر لأن الجسم يتحرك في حركة دائرية.
تعمل قوة الشد في اتجاه المركز، لذلك ليس من الصحيح تحليلها ، يجب أن نحلل قوة الجاذبية في اتجاه مماسي ومركزي
واكتب معادلة الحركة المركزية والمماسية وفقًا لذلك.
3. مكتوب أن مقاومة الهواء مهملة، وبالتالي يتم حفظ الطاقة الميكانيكية. وارتفاع النقطة 5 هو ارتفاع النقطة 1 ، وإلا ستكون النقطة 5 أقل.
המהירות לא מעידה בגודלה על גודל התאוצה.
בשאלה זאת אפשר להעריך היכן המהירות גדולה והיכן המהירות קטנה, מזה לבד לא ניתן ללמוד על התאוצה המשיקית.
2. יש לבצע הפרדה לכוח הכובד ולא לכוח המתיחות מכיוון שהגוף נע בתנועה מעגלית.
כוח המתיחות פועל בכיוון רדיאלי, לכן לא נכון לפרק אותו ,יש לפרק את כוח הכובד לכיוון משיקי ורדיאלי
ולכתוב בהתאם את משוואת התנועה הרדיאלית והמשיקית.
______________________________________________________________________________________

______________________________________________________________________________________
...
يكون مقدار السرعة المماسية قصوى في أدنى نقطة - النقطة 3.
من اعتبارات الطاقة - من حفظ الطاقة، هناك علاقة بين ارتفاع ومقدار السرعة المماسية.
من الديناميكا - يتعلق اتجاه التغيير في السرعة المماسية على اتجاه القوة المماسية.
מדינמיקה - מגמת השינוי במהירות המשיקית תלויה בכיון הכוח המשיקי.
القوة الوحيدة التي تعمل هي الجاذبية ، وبالتالي يتم حفظ الطاقة الميكانيكية
مجموع الطاقة الحركية والطاقة الوضعية ثابت أينما كان الجسم.
كلما كان الجسم في ارتفاع أقل ، كلما قلت طاقته الوضعية وزادت طاقته الحركية.
لذلك ، كلما انخفض الجسم زادت سرعته.
مقدار السرعة المماسية يكون الأقصى، في أدنى نقطة ، النقطة 3.
طريقة اخرى :
يعمل مركّب الجاذبية في الاتجاه المماسي للحركة أثناء حركة الجسم من النقطة 1 إلى النقطة 3 ، وفي عكس اتجاه الحركة من النقطة 3 إلى النقطة 5.
تزداد السرعة من النقطة 1 إلى النقطة 3 وتنخفض من النقطة 3 إلى النقطة 5. في النقطة 3 ، يكون مقدار السرعة قصوى.
סכום האנרגיה הקינטית והאנרגיה הפוטנציאלית הוא קבוע בכל מקום בו נמצא הגוף.
ככל שהגוף נמצא במקום נמוך יותר כך האנרגיה הפוטנציאלית קטנה יותר והאנרגיה הקינטית גדולה יותר.
לכן , ככל שהגוף נמצא במקום נמוך יותר כך מהירותו גדולה יותר.
גודל המהירות המשיקית מרבי, בנקודה הנמוכה ביותר נקודה 3.
التسارع المماسي هو تسارع في اتجاه مماسي للحركة، والتسارع المركزي هو تسارع في اتجاه عمودي على الحركة.
السرعة المماسية هي السرعة في اتجاه مماس للحركة ، والسرعة بشكل عام مماسة للحركة.
يمكن أن تكون للجسم مركّب سرعة مركزية عندما يتحرك الجسم في حركة دائرية بنصف قطر متغير.
מהירות משיקית היא מהירות בכיוון משיק לתנועה , מהירות באופן כללי היא משיקה לתנועה.
מהירות רדיאלית יכולה להיות כאשר גוף נע בתנועה מעגלית ברדיוס תנועה משתנה.
______________________________________________________________________________________

______________________________________________________________________________________
...
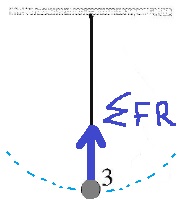
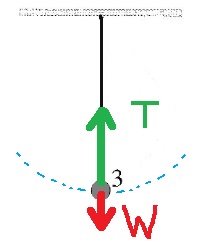
في النقطة 3 يكون شد الخيط أكبر من قوة الجاذبية.
تتحرك الكرة في حركة دائرية ، وفي أي حركة دائرية يجب أن تكون هناك قوة جاذبة نحو المركز.
منذ اللحظة التي يتم فيها تحرير الكرة تتحرك الكرة في حركة دائرية. أيضًا في النقطة 3 يتحرك الجسم في حركة دائرية.
في الحركة الدائرية ، في أي نقطة في مسار الحركة ، يجب أن تعمل القوة الجاذبة تجاه مركز الدوران ، لذلك عند النقطة 3 يجب أن تكون قوة الشد أكبر من قوة الجاذبية. كما ترى في الرسم البياني التالي:
בתנועה מעגלית בכל נקודה במסלול התנועה חייב לפעול כוח צנטריפטלי לכיוון מרכז הסיבוב , לכן בנקודה 3 כוח המתיחות חייב להיות גדול מכוח הכובד. כפי שניתן לראות בתרשים הבא:
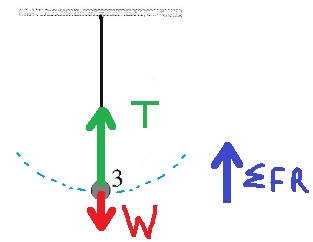
1. في النقطة 3 ، تكون القوى متعاكسة، ولا توجد حركة في الاتجاه الرأسي. لذلك يمكن أن تنسوا أنها حركة دائرية.
وتعتقدوا خطأ أن محصلة القوى في الاتجاه الرأسي هو صفر. وتتوصلوا إلى نتيجة خاطئة مفادها أن قوة التوتر هي نفس قوة الجاذبية.
2. يمكنك كتابة معادلة الحركة الدائرية للكرة عندما تمر عبر النقطة 3 ، وفهم أي القوى أكبر منها:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»mg«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»mg«/mi»«mspace linebreak=¨newline¨»«/mspace»«/math»
لذلك ، من معادلة الحركة الدائرية ، تكون قوة الشد أكبر من قوة الجاذبية.
ולחשוב בטעות ששקול הכוחות בכיוון האנכי הוא אפס. ולהגיע למסקנה השגויה שכוח המתיחות זהה בגודלו לכוח הכובד.
______________________________________________________________________________________

______________________________________________________________________________________
...
تعبير مقدار محصلة القوى هو: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨»§#931;F«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»h«/mi»«/mrow»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«/math»
معادلة الحركة الدائرية والتعبير عن السرعة في المعادلة بمساعدة حفظ الطاقة.
القوة المحصّلة في النقطة 3 هي قوة الجاذبية:
نكتب معادلة الحركة الدائرية في اللحظة التي تتجاوز فيها الكرة النقطة 3:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
فقط قوة الجاذبية التي تبذل شغل، لذا يتم حفظ الطاقة الميكانيكية.
نكتب معادلة حفظ الطاقة، نقارن بين الطاقة الكلية في النقطة 1 بالطاقة الكلية في النقطة 3.
ونعبر عن V3 من معادلة حفظ الطاقة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msub»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msub»«/math»
تحرّر الكرة من حالة السكون ، والطاقة الحركية في النقطة 1 تساوي صفرًا.
نختار مستوى الانتساب في مستوى النقطة 3 ، بحيث تكون الطاقة الوضعية في النقطة 3 مساوية للصفر.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«msub»«mi mathvariant=¨bold¨»K«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»h«/mi»«/msqrt»«/math»
نعوّض التعبير عن السرعة V3 ، في تعبير القوة الجاذبة نحو المركز:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msqrt»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»h«/mi»«/msqrt»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»h«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
نصف قطر الحركة الدائرية R يساوي طول الخيط L ، نعوّض طول الخيط بدلاً من نصف قطر المسار:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»h«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»§#931;F«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»h«/mi»«/mrow»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«/menclose»«/math»
تعبير مقدار محصلة القوى هو: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»h«/mi»«/mrow»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«/math»
נכתוב את משוואת התנועה המתאימה לרגע זה:
1. التعبير الذي حصلنا عليه ليس متجهًا ، فهو يصف مقدار القوة المحصّلة وليس اتجاهها.
2. عندما يتطلب الأمر تطوير تعبير وفقًا لمقادير معينة ، يجب تطوير تعبير يحتوي فقط على كل تلك المقادير والثوابت.
2. כאשר נדרש לפתח ביטוי בהתאם לגדלים מסוימים, יש לפתח ביטוי המכיל רק את כל אותם גדלים, וקבועים.
2. בכל נקודה בה הכדור נמצא פועל כוח מתיחות שונה בגודלו ובכיוונו.
לכן לכל נקודה קיים תרשים כוחות שונה ומשוואת תנועה שונה. הנקודה הנמוכה ביותר היא הנקודה הקלאסית בשאלות הבגרות.
3. יש לפתח את הביטוי בתלות בכל הפרמטרים המבוקשים בלבד.
4. לאחר כתיבת הביטוי, אם יש קצת זמן.. מומלץ לבדוק שהביטוי תקין מבחינת יחידות.
______________________________________________________________________________________

______________________________________________________________________________________
...
زمن الحركة متساوٍ: t1 = t2.
تتحرك الكرتان في رمي أفقي، ويمكن التعبير عن زمن الحركة من الحركة العمودية، وفقًا لمبدأ استقلالية الحركات.
في كلتا الحالتين تتحرك الكرات في رمي أفقي، من مبدأ استقلالية الحركات يحدّد زمن الحركة بواسطة الحركة العمودية.
نكتب تعبيرًا لزمن الحركة، من الحركة العمودية ، نشير إلى المحور الذي يكون أصله في نقطة بداية الحركة واتجاهه إلى الأسفل.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«msub mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«/math»
التسارع في الاتجاه العمودي هو تسارع الجاذبية g ، والسرعة الابتدائية في الاتجاه العمودي تساوي صفر ، وحسب موقع أصل المحور المحدد ، يكون الموقع العمودي الابتدائي صفرًا.
قيمة الموقع الرأسي في نهاية الحركة تساوي الارتفاع الذي يُلقى منه الجسم ، ونعبر عن زمن الحركة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»y«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«msub»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»h«/mi»«/mrow»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«/msqrt»«/math»
يتعلق زمن الحركة على ثابت الجاذبية والارتفاع الابتدائي. نظرًا لأن الكرات في كلتا الحالتين بدأت تتحرك من نفس الارتفاع - فإن زمن الحركة هو نفسه.
נכתוב ביטוי לזמן התנועה , מהתנועה האנכית, נתייחס לציר שראשיתו בנקודת תחילת התנועה וכיוונו כלפי מטה.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«msub mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«/math»
התאוצה בכיוון האנכי היא תאוצת הכובד היא g , המהירות ההתחלתית בכיוון האנכי שווה לאפס , ובהתאם למיקום ראשית הציר הנבחר , המיקום האנכי ההתחלתי הוא אפס.
ערך המיקום האנכי בסוף התנועה שווה לגובה ממנו נזרק הגוף, נבטא את זמן התנועה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»y«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«msub»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»h«/mi»«/mrow»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«/msqrt»«/math»
בהתאם לגובה ממנו נזרקו הכדורים ,מכיוון שהגובה זהה בשני המקרים זמן התנועה זהה.
ليست هناك حاجة لتطوير تعبير لزمن للحركة ، يكفي أن تشير أن الحركة العمودية هي نفسها في كلتا الحالتين ، وبالتالي فإن زمن الحركة هو نفسه.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac»«msub»«mi mathvariant=¨bold¨»D«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»D«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mn mathvariant=¨bold¨»2«/mn»«/msqrt»«/math»
يمكن التعبير عن المسافات الأفقية في كل تجربة باستخدام مبدأ استقلالية الحركات ، ويمكن إيجاد النسبة بين هذه المسافات.
.
نعبر عن كل من المسافتين D1 و D2 ، باستخدام مبدأ استقلالية الحركات. وإيجاد النسبة بين هاتين المسافتين.
في كلتا التجربتين عندما تصل الكرة إلى النقطة 3 يكون لها سرعة مختلفة ، هذه السرعة هي سرعة الرمي الأفقية.
نُشير لسرعة الرمي في التجربة 1 بـ V31 ، وسرعة الرمي في التجربة الثانيةبـ V32.
وجدنا تعبيرًا لهذه السرعة في القسم "جـ" : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»h«/mi»«/msqrt»«/math» , h هو الارتفاع فوق النقطة 3 التي تم تحرير الكرة منها.
نعبر عن المسافة الأفقية D1 ، في التجربة الأولى عندما تحرّر الكرة من ارتفاع h:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»D«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«msub mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»h«/mi»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«/math»
نعبّر عن المسافة الأفقية D2 ، في التجربة الثانية، عندما تحرّر الكرة من ارتفاع 0.5h:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»D«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«msub mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfrac»«mi mathvariant=¨bold¨»h«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«/math»
أوجد النسبة بين المسافتين الأفقيتين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»D«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»D«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msqrt»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»h«/mi»«/msqrt»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mrow»«msqrt»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mstyle displaystyle=¨true¨»«mfrac»«mi mathvariant=¨bold¨»h«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«/mstyle»«/msqrt»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/math»
بعد عمليات الاختزال :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»D«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»D«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msqrt»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike updiagonalstrike¨»«mi mathvariant=¨bold¨»h«/mi»«/menclose»«/msqrt»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/menclose»«/mrow»«mrow»«msqrt»«menclose notation=¨horizontalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mstyle displaystyle=¨true¨»«mfrac»«menclose notation=¨downdiagonalstrike updiagonalstrike¨»«mi mathvariant=¨bold¨»h«/mi»«/menclose»«menclose notation=¨horizontalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/mfrac»«/mstyle»«/msqrt»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/menclose»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mfrac»«msub»«mi mathvariant=¨bold¨»D«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»D«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mn mathvariant=¨bold¨»2«/mn»«/msqrt»«/menclose»«/math»
لذلك ، عندما يكون الارتفاع الذي تنطلق منه الكرة أكبر بمرتين، تزداد المسافة الأفقية بمقدار «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«/msqrt»«/math» .
בכל אחד משני הניסויים כאשר הכדור מגיע לנקודה 3 יש לו מהירות שונה, מהירות זו היא מהירות הזריקה האופקית.
נסמן את מהירות הזריקה בניסוי 1 ב V31 , ואת מהירות הזריקה בניסוי השני ב V32 .
בסעיף ג' מצאנו ביטוי למהירות זאת : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»h«/mi»«/msqrt»«/math» , h הוא הגובה מעל נקודה 3 ממנו שוחרר הכדור.
נבטא את המרחק האופקי D1 , בניסוי הראשון כאשר הכדור משוחרר מגובה h:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»D«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«msub mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»h«/mi»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«/math»
נבטא את המרחק האופקי D2 , בניסוי השני ,כאשר הכדור משוחרר מגובה 0.5h :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»D«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«msub mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfrac»«mi mathvariant=¨bold¨»h«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«/math»
נמצא את היחס בין המרחקים האופקיים:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»D«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»D«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msqrt»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»h«/mi»«/msqrt»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mrow»«msqrt»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mstyle displaystyle=¨true¨»«mfrac»«mi mathvariant=¨bold¨»h«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«/mstyle»«/msqrt»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/math»
נבצע פעולות צמצום, זמני התנועה גם זהים , לכן אפשר לצמצמם גם אותם:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»D«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»D«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msqrt»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike updiagonalstrike¨»«mi mathvariant=¨bold¨»h«/mi»«/menclose»«/msqrt»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/menclose»«/mrow»«mrow»«msqrt»«menclose notation=¨horizontalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mstyle displaystyle=¨true¨»«mfrac»«menclose notation=¨downdiagonalstrike updiagonalstrike¨»«mi mathvariant=¨bold¨»h«/mi»«/menclose»«menclose notation=¨horizontalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/mfrac»«/mstyle»«/msqrt»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/menclose»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mfrac»«msub»«mi mathvariant=¨bold¨»D«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»D«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mn mathvariant=¨bold¨»2«/mn»«/msqrt»«/menclose»«/math»
לכן כאשר הגובה ממנו משחררים את הכדור גדול פי 2, המרחק האופקי גדל פי שורש 2.
1. ليست هناك حاجة لتكرار تطوير تعبير سرعة الرمي الذي تم تطويره في القسم ج.
2.زمني الحركة هي نفسها ولكن المسافتان مختلفتان.
3. الارتفاع في التجربة الأولى أكبر بمرتين ، لكن سرعة الرمي في التجربة الأولى ليست أكبر بمرتين من سرعة الرمي في التجربة الثانية.
4. لم يتم توضيح كيف انفصلت الكرة، ليس لها أهمية، من المهم أن نفهم أنه بعد الانفصال يتحرك الجسم في رمي أفقي.
5. عندما ينتقل جسم من حركة معينة إلى حركة أخرى نتيجة لحدث ما ، طالما لم تكن هناك قوة تعمل في اتجاه الحركة في أثناء الحدث
سرعة الجسم لا تتغير.
في هذه الحالة ، غير مكتوب أنه عندما تنفصل الكرة عن الخيط ، تعمل قوة أفقية ، لذلك نفترض أن السرعة التي تصل إليها الكرة
هي سرعة الرمي الأفقية.
2. זמני התנועה זהים אך המרחקים שונים .
3. הגובה בניסוי הראשון גדול פי 2 , אך מהירות הזריקה בניסוי הראשון לא גדולה פי 2 ממהירות הזריקה בניסוי השני.
4. לא מוסבר כיצד הכדור ניתק, אין לכך חשיבות, חשוב להבין שלאחר ההתנתקות הגוף נע בזריקה אופקית.
5. כאשר גוף עובר מתנועה מסוימת לתנועה אחרת כתוצאה מאירוע כלשהו, כל עוד לא פועל כוח בכיוון התנועה בזמן האירוע
מהירות הגוף לא משתנה.
במקרה זה לא כתוב שבזמן הינתקות הכדור מהחוט פועל כוח אופקי , לכן אנחנו מניחים שהמהירות אליה מגיע הכדור
היא מהירות הזריקה האופקית.
______________________________________________________________________________________