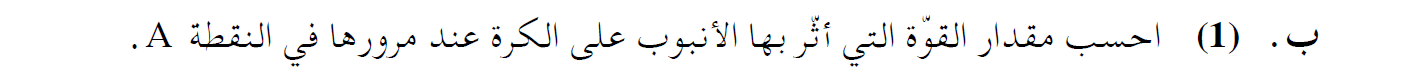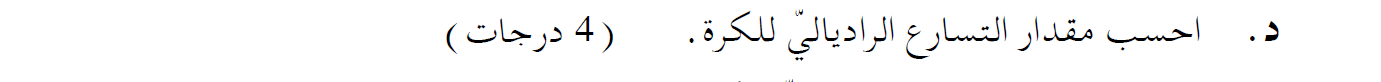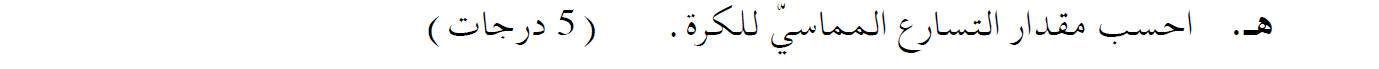______________________________________________________________________________________
...
مقدار قوة الجاذبة نحو المركز المؤثرة على الكرة 0.64 نيوتن.
معادلة الحركة الدائرية
عندما يجتاز النقطة A فإنه يتحرك في حركة دائرية. نجد القوة الجاذبة نحو المركز باستخدام معادلة الحركة الدائرية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»05«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«msup»«mn mathvariant=¨bold¨»2«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»64«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/math»
مقدار قوة الجاذبة نحو المركز المؤثرة على الكرة 0.64 نيوتن.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»05«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«msup»«mn mathvariant=¨bold¨»2«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»64«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/math»
גודלו של הכוח הצנטריפטאלי הפועל כל הכדור הוא 0.64 ניוטון.
السرعة الأفقية للكرة قبل دخولها الأنبوب هي سرعتها الخطية في الحركة الدائرية في النقطة A. لأنه لا توجد قوى أفقية تعمل على تغيير مقدار سرعتها.
بمجرد دخول الكرة إلى الأنبوب ، يشغّل الأنبوب قوة عمودية على الحركة. في النقطة A توجد قوة عمودية فقط.
ברגע שהכדור נכנס לצינור הצינור מפעיל כוח מאונך לתנועה. בנקודה A פועל כוח אנכי בלבד.
______________________________________________________________________________________
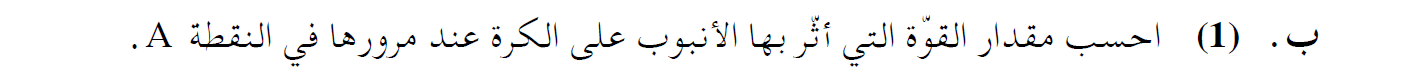
______________________________________________________________________________________
...
يجب أن يكون مقدار القوة العمودية التي يشغّلها الأنبوب 0.14 نيوتن للأسفل.
فقط القوة العمودية التي يشغّلها الأنبوب وقوة الجاذبية على الكرة ، يجب أن يكون محصلة هاتين القوتين في الاتجاه نحو مركز الدوران 0.64 نيوتن.
كما وجدنا في القسم السابق.
כפי שמצאנו בסעיף קודם.
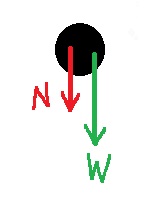
تتأثر الكرة بقوة الجاذبية والقوة التي يشغّلها الأنبوب. هذه القوة هي القوة العمودية.
أينما كانت الكرة ، تعمل قوة الجاذبية لأسفل ، في النقطة A يكون اتجاه قوة الجاذبية نحو المركز.
تلتصق الكرة بجدار الأنبوب ، ويشغّل الجدار قوة عمودية متعامدة على الحركة ، وتعمل هذه القوة دائمًا في اتجاه الجاذب نحو المركز.
نحسب مقدار قوة الجاذبية: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»05«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/math»
في النقطة A ، يكون مقدار القوة الجاذبة نحو المركز 0.64 نيوتن. يجب أن يشغّل الأنبوب قوة لأسفل عند النقطةA "لمساعدة" قوة الجاذبية بحيث تكون الحركة الدائرية في النقطة A ممكنة.
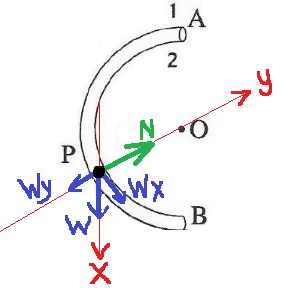
لنرسم مخططًا للقوى المؤثرة على الكرة عندما تمر بالنقطة A:
لكي يتحرك الجسم في حركة دائرية في النقطة A. وفقًا لمعطيات الحركة وكتلة الكرة ، يجب أن يكون مقدار القوة الجاذبة نحو المركز 0.64 نيوتن.
نظرًا لأن مقدار قوة الجاذبية هو 0.5 نيوتن ، يجب أن يكون مقدار القوة العمودية التي يشغّلها الأنبوب 0.14 نيوتن للأسفل.
כוח הכובד פועל כלפי מטה , בנקודה A כיוון כוח הכובד הוא צנטריפטאלי.
הכדור נצמד לדופן הצינור , הדופן מפעילה כוח נורמל ניצב לתנועה , כוח זה פועל תמיד בכיוון צנטריפטאלי.
נחשב את גודלו של כוח הכובד: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»05«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/math»
בנקודה A גודלו של הכוח הצנטריפטאלי הוא 0.64 ניוטון. הצינור חייב להפעיל בנקודה A כוח כלפי מטה "לעזור" לכוח הכובד כדי שתתאפשר התנועה המעגלית בנקודה A.
נערוך תרשים כוחות על הכדור כאשר הוא חולף בנקודה A:
כדי שהגוף ינוע בתנועה מעגלית בנקודה A.
נערוך תרשים כוחות:
في هذه الحالة ، قبل رسم مخطط القوى ، يجب أن نفهم أنه وفقًا لمقدار القوة الجاذبة نحو المركز ووفقًا لاتجاه قوة الجاذبية ، يجب أن تعمل القوة التي يشغّلها الأنبوب نحو الأسفل. وعندئذ فقط نضف قوة الأنبوب إلى الرسم التخطيطي لأسفل.
تعد مرحلة رسم مخطّط للقوى المؤثرة مرحلة حرجة ، ومن المهم التحقق بعناية من القوى التي تعمل ، وما هو اتجاه كل من القوى.
במקרה זה, לפני עריכת תרשים הכוחות חייבים להבין שבהתאם לגודלו של הכוח הצנטריפטאלי ובהתאם לכיוון כוח הכובד , הכוח שהצינור מפעיל חייב לפעול כלפי מטה . ורק אח"כ להוסיף את כוח הצינור לתרשים כלפי מטה.
שלב עריכת תרשים הכוחות הוא שלב קריטי , חשוב לבדוק היטב מי הכוחות הפועלים , ומה הכיוון של כל אחד מהכוחות.
______________________________________________________________________________________
ب. 
______________________________________________________________________________________
...
الجانب 1 .
اتجاه القوة واضح من القسم السابق، حسب موقع الكرة ، من الممكن فهم أي جانب من الأنبوب يشغّل القوة.
لكي يشغّل الأنبوب قوة نحو الأسفل، بسبب أن الكرة داخل الأنبوب - الجانب 1 هو الجانب الذي يشغّل القوة على الكرة.
يشغّل جدار الأنبوب قوة عمودية ، في اتجاه عمودي على الحائط ، عندما تكون الكرة داخل الأنبوب في النقطة A.
يشغّل الجانب 1 قوة لأسفل ، بينما يشغّل الجانب 2 قوة نحو الأعلى على الكرة.
דופן 1 מפעילה כוח כלפי מטה , דופן 2 מפעילה כוח על הכדור כלפי מעלה.
______________________________________________________________________________________

______________________________________________________________________________________
...
سرعة الكرة في النقطة P تساوي 5.85 مترًا في الثانية.
فقط قوة الجاذبية هي التي تعمل، من معادلة حفظ الطاقة يمكن التعبير عن سرعة الكرة في النقطة P.
يشغّل الأنبوب قوة عمودية على حركة الكرة، من تعريف الشغل هذه القوة لا تعمل شغل. القوة الوحيدة التي تعمل شغل هي قوة الجاذبية.
لذلك تُحفظ الطاقة الميكانيكية:
لنقارن الطاقة الميكانيكية في النقطة A بالطاقة الميكانيكية في النقطة P:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»P«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«/math»
نُعبّر عن السرعة VA من معادلة حفظ الطاقة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfenced mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»p«/mi»«/msub»«/mrow»«/mfenced»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»p«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced»«mrow»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»p«/mi»«/msub»«/mrow»«/mfenced»«/msqrt»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
ارتفاع النقطة A يساوي ضعف نصف قطر الدوران ، والسرعة في النقطة A وارتفاع النقطة P مذكورة في السؤال.
نُعوّض هذه المعطيات في التعبير الذي طوّرناه:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced»«mrow»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»p«/mi»«/msub»«/mrow»«/mfenced»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»p«/mi»«/msub»«/mrow»«/mfenced»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«msup»«mn mathvariant=¨bold¨»2«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«/mfenced»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»34«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»24«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»85«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«/math»
سرعة الكرة في النقطة P تساوي 5.85 مترًا في الثانية.
לכן האנרגיה המכנית נשמרת:
נשווה בין האנרגיה המכנית בנקודה A לאנרגיה המכנית בנקודה P:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»P«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«/math»
נבטא ממשוואת שימור האנרגיה את המהירות VA:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfenced mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»p«/mi»«/msub»«/mrow»«/mfenced»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»p«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced»«mrow»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»p«/mi»«/msub»«/mrow»«/mfenced»«/msqrt»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
גובה הנקודה A שווה לפעמיים רדיוס הסיבוב, המהירות בנקודה A נתונה בשאלה.
נמצא את גובה הנקודה P
إذا كان الأنبوب أوسع بكثير من قطر الكرة، فإن الكرة ستسقط داخل الأنبوب، وفي هذه الحالة سيشغّل الأنبوب قوة عمودية متعامدة لسطح الأنبوب ولا يكون متعامدًا مع الحركة. لن يتم حفظ الطاقة الميكانيكية. لهذا السبب نقول "قطر الكرة أصغر قليلاً من الأنبوب" لذا فإن الكرة قريبة من الأنبوب. والقوة العمودية متعامدة على الحركة.
______________________________________________________________________________________
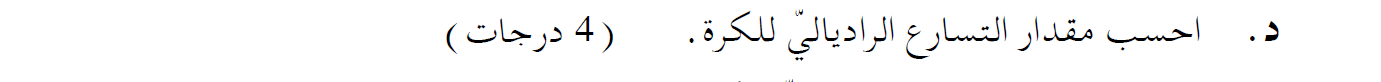
______________________________________________________________________________________
...
التسارع المركزي للكرة في النقطة P يساوي 42.77 مترًا لكل ثانية مربعة.
تعبير التسارع المركزي (راديالي).
يتعلق مقدار التسارع المركزي في نقطة ما في الحركة الدائرية على مقدار السرعة الخطية في تلك النقطة.
وفقًا لتعبير التسارع المركزي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»p«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»p«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«msup»«mn mathvariant=¨bold¨»85«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»42«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»77«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
التسارع المركزي للكرة في النقطة P تساوي 42.77 مترًا لكل ثانية مربعة.
לפי ביטוי התאוצה הרדיאלית:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»p«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»p«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«msup»«mn mathvariant=¨bold¨»85«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»42«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»77«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
התאוצה הרדיאלית של הכדור בנקודה P היא 42.77 מטר לשנייה בריבוע.
1. تعبير التسارع المركزي مناسب لأي حركة دائرية ، حتى للحركة الدائرية غير الدورية.
2. التعبير مُدرج في أوراق القوانين ، ولا داعي لتطويره.
3. من خلال ضرب تعبير التسارع المركزي في كتلة الجسم المتحرك في حركة دائرية ، نحصل على معادلة الحركة الدائرية.
2. הביטוי נתון בדפי הנוסחאות, אין צורך לפתח אותו.
3. מהכפלת ביטוי התאוצה הרדיאלית במסת הגוף הנע בתנועה מעגלית , מתקבלת משוואת התנועה המעגלית.
______________________________________________________________________________________
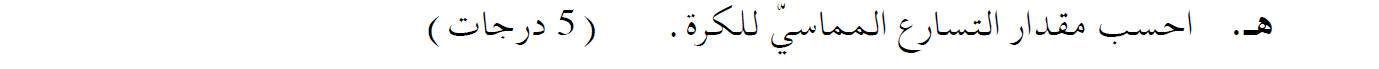
______________________________________________________________________________________
...
مقدار التسارع المماسي في النقطة P يساوي 8.66 مترًا لكل ثانية مربعة.
مركّب قوة الجاذبية في اتجاه الحركة هو القوة التي تسبب التسارع المماسي.
ينتج التسارع المماسي من القوة المماسّية - وهي قوة تعمل في اتجاه الحركة.
في هذه الحالة ، القوة المماسة هي ومركّب الجاذبية في الاتجاه المماس للمسار.
نرسم مخططًا للقوى ، ونختار هيئة من المحاور حيث يكون المحور X مماسًا للمسار في اتجاه مركّب قوة الجاذبية المماسّية ، ويكون المحور Y في اتجاه القوة العمودية:
نرسم مخططًا للقوى ، ونختار مجموعة من المحاور حيث يكون المحور X مماسًا للمسار في اتجاه مركب قوة الجاذبية المماسّية ، ويكون المحور Y في اتجاه القوة العمودية:
الزاوية بين قوة الجاذبية W ومركّب قوة الجاذبية WX هي الزاوية المركزية بين نصف القطر OB ونصف القطر OP.
نجد هذه الزاوية المركزية.
لنحدد الارتفاع بين نقطة مركز الدوران O وارتفاع hp بـ X.
دعونا نحدّد الزاوية المركزية Θ ونجد مقدارها:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»x«/mi»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»P«/mi»«/msub»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Rcos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»P«/mi»«/msub»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»60«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#176;«/mo»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math» 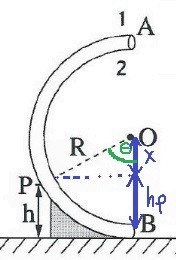
أضف الزاوية المركزية إلى مخطّط القوى ، ونجد التسارع المماسي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#931;F«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»W«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»mg«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#952;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»60«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»66«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math» 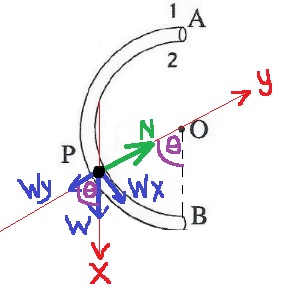
إذن ، مقدار التسارع المماسي في النقطة P يساوي 8.66 مترًا لكل ثانية مربعة.
במקרה זה הכוח המשיקי הוא רכיב כוח הכובד בכיוון המשיק למסלול.
נערוך תרשים כוחות , נבחר מערכת צירים שבה ציר X משיק למסלול בכיוון רכיב כוח הכובד המשיקי , וציר Y בכיוון כוח הנורמל:
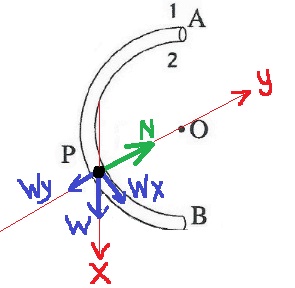
1. لإيجاد التسارع المماسي في النقطة P ، يمكننا افتراض أن النقطة تقع على مستوى مائل.
زاوية ميل المستوى هي الزاوية المركزية التي وجدناها.
2. يعتبر هذا القسم قسمًا صعبًا ، والتحدي هندسي ، وعادة ما يكون التحدي في كل سؤال محجوزًا للقسم الأخير من السؤال.
3. للتعامل مع التحدي الهندسي بفاعلية ، يوصى بمحاولة التعامل معه في صفحة المسودة .
في صفحة المسودة هناك شعور بأن الأخطاء مسموح بها. لذلك ، فإن فرصة التوصل إلى حل أكبر.
حتى في صفحة المسودة ، من المهم العمل بطريقة منظمة.
4. العلاقة بين ارتفاع النقطة P والزاوية المركزية تتكرر في حلول أسئلة البجروت في حركة دائرية بمستوى عمودي.
5. أحيانًا يفهم الطلاب الفيزياء جيدًا ولكن في الرياضيات أو الهندسة ، هناك شيء لا يعمل "ويتعثر"
في مثل هذه الحالة، من المهم تقديم حل كامل، بدون الجزء الرياضي أو الهندسي. من الممكن تحديد أي قيمة للزاوية ومتابعة الحل حتى يتم الحصول على قيمة التسارع المماسي. على الأرجح لن تكون الإجابة صحيحة ، لكنك ستحصل على معظم النقاط.
זווית נטיית המישור היא הזווית המרכזית אותה מצאנו .
2. סעיף זה נחשב לסעיף מאתגר, האתגר הוא גיאומטרי , האתגר בכל שאלה שמור לרוב סעיף האחרון בשאלה.
3. כדי להתמודד עם האתגר הגיאומטרי בצורה יעילה מומלץ לנסות ולהתמודד בדף טיוטה .
בדף טיוטה יש הרגשה שמותר לטעות. לכן הסיכוי להגיע לפתרון יותר גדול.
גם בדף טיוטה חשוב לעבוד בצורה מסודרת .
4. הקשר שבין גובה הנקודה P והזווית המרכזית חוזר על עצמו בפתרונות של שאלות הבגרות בתנועה מעגלית אנכית.
5. לפעמים תלמידים מבינים היטב את הפיזיקה אבל במתמטיקה או בגיאומטריה משהו לא מסתדר ."ונתקעים"
במקרה כזה חשוב להציג פתרון מלא , ללא החלק המתמטי או הגיאומטרי . אפשר לקבוע ערך כל שהוא לזווית ולהמשיך את הפתרון עד לקבלת ערך התאוצה המשיקית. ככל הנראה התשובה לא תהיה נכונה, אך תקבלו את רוב הנקודות.
______________________________________________________________________________________