حل التدريبات العملية: الحركة التوافقية البسيطة في نابض أفقي وبندول بسيط

تتحرك الكرة تحت تأثير قوتين فقط: القوة العمودية وقوة الجاذبية.

نرمز للنقطة التي بدأت منها الكرة بالحركة بـ A،
ولنقطة أسفل الأنبوب بـ B،
ولنقطة الطرف الأخرى بـ C.

تؤثر القوة العمودية باتجاه مركز الدوران،
ونقوم بإجراء تحليل لقوة الجاذبية.

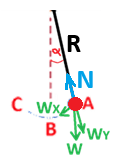
عندما تكون زاوية ميل الخيط صغيرة، تتحرك الكرة تقريبًا في خط مستقيم، وتكون النقطة $\mathrm{<span\; class=""\; id="yui\_3\_17\_2\_1\_1750797201681\_16689"\; style="font-size:\; large;\; color:\; rgb(0,\; 61,\; 245);">B</span>}$BB تقريبًا نقطة الاتّزان.

القوة المحصلة المؤثرة على الكرة هي مركبة قوة الجاذبية التي تؤثر دائمًا باتجاه النقطة $\mathrm{<span\; class=""\; id="yui\_3\_17\_2\_1\_1750797201681\_16693"\; style="font-size:\; large;\; color:\; rgb(0,\; 61,\; 245);">B</span>}$BB كقوة معيدة.

نكتب تعبيرًا للقوة المحصلة:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»w«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«/msub»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mstyle»«/math»

نصف القوة المحصلة المؤثرة على الكرة بالنسبة لمحور أصلُه في نقطة الاتّزان $B$B واتجاهه نحو اليمين، كما هو موضّح في الرسم التالي :

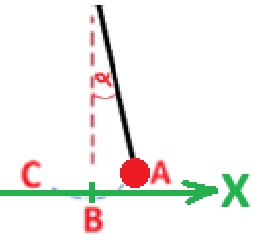
بالتقريب لزوايا صغيرة، يتحقّق: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«/mstyle»«/math», نكتب وفقًا لذلك تعبير القوة المحصلة:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«/mstyle»«/math»

نعبّر عن زاوية ميل الخيط كزاوية مركزية بدلالة نصف قطر الدوران وموقع الكرة (الذي يساوي تقريبًا طول القوس)

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»X«/mi»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/mstyle»«/math»

نظرًا لإمكانية اعتبار حركة الكرة حركة في خط مستقيم تكون فيها القوة المحصلة قوة معيدة تتناسب طرديًا مع موقع الكرة، فإن حركة الكرة تُعد تقريبًا حركة توافقية بسيطة