حل التدريبات العملية: الحركة التوافقية البسيطة في نابض أفقي وبندول بسيط: 6.1

6.1

في حركة البندول البسيط، تؤثر على الجسم قوتان: قوة الشد وقوة الجاذبية.

قوة الشد تؤثر في اتجاه نقطة مركز الدوران. نقوم بتحليل قوة الجاذبية إلى مركبتين متعامدتين:

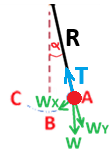
عندما تكون زاوية ميل الخيط صغيرة، يتحرك الجسم تقريبًا في خط مستقيم، وتكون النقطة B تقريبًا نقطة الاتزان.

القوة المحصلة المؤثرة على الجسم هي مركبة قوة الجاذبية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«/math» والذي يؤثر دائمًا في اتجاه النقطة B كقوة مُرجعة.

نكتب تعبيرًا للقوة المحصلة:

نصِف القوة المحصلة المؤثرة على الجسم بالنسبة لمحور أصله في نقطة الاتزان B واتجاهه نحو اليمين، كما هو موضح في الرسم التالي:

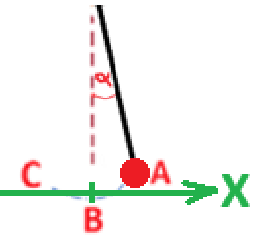
بالقرب من الزوايا الصغيرة، يتحقق التقريب التالي «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«/mstyle»«/math», نكتب وفقًا لذلك تعبير القوة المحصلة:

نُعبّر عن زاوية ميل الخيط كزاوية مركزية بدلالة طول الخيط وموقع الجسم (والذي يُساوي تقريبًا طول القوس).

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»X«/mi»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/mstyle»«/math»

لذلك في الحالة الأولى يمكن اعتبار حركة الجسم كحركة في خط مستقيم يكون فيها القوة المحصلة قوة مُرجعة تتناسب طرديًا مع موقع الجسم. حركة الجسم في الحالة الأولى هي تقريبًا حركة توافقية بسيطة.

للتوسع: الافتراض الأول بأن الجسم يتحرك في خط مستقيم، والافتراض الثاني بأن زاوية ميل الخيط تساوي sin الزاوية هما في الواقع نفس الافتراض.

انطلاقًا من مبادئ الحركة الدائرية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»s«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/math» بالقرب من الزوايا الصغيرة، يكون طول القوس مساويًا تقريبًا لموقع الجسم، ويتحقق: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»s«/mi»«/mstyle»«/math» .

نُعبّر عن sin زاوية ميل الخيط: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»X«/mi»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/math». لذلك، عندما افترضنا أن الجسم يتحرك في خط مستقيم، فقد افترضنا أيضًا أن قيمة جيب الزاوية تساوي قيمة الزاوية نفسها.