حلول التدريبات العملية الديناميكا لجسمين
| الموقع: | YouCube |
| المقرر: | דינמיקה בקו ישר - ערבית |
| كتاب: | حلول التدريبات العملية الديناميكا لجسمين |
| طبع بواسطة: | משתמש אורח |
| التاريخ: | الأربعاء، 4 فبراير 2026، 2:43 AM |
جدول المحتويات
- 1. جسمان يتحركان على سطح أفقي
- 2. جسمان يتحركان على سطح أفقي غير أملس
- 3. قوة تعمل بزاوية
- 4. جسمان معلقان بواسطة بكرة
- 5. جسم معلق وجسم آخر على سطح أفقي أملس
- 6. جسم معلق وجسم آخر على سطح أفقي غير أملس
- 7. قوة خارجية تؤثر على الخيط
- 8. جسم معلق وجسم آخرعلى سطح مائل أملس
- 9. جسم معلق وجسم آخر معلق على سطح مائل غير أملس
- 10. جسمان على سطحين مائلين
- 11. جسمان موصولان يسقطان في سقوط حر
1. جسمان يتحركان على سطح أفقي
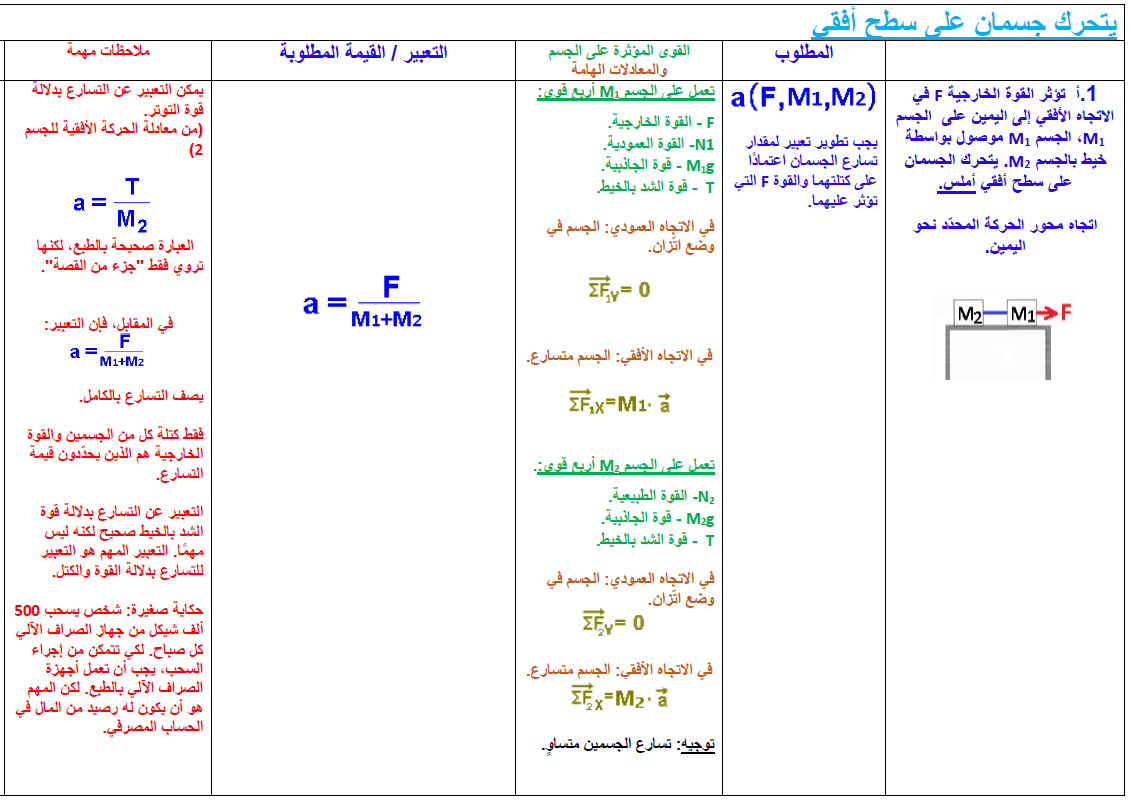
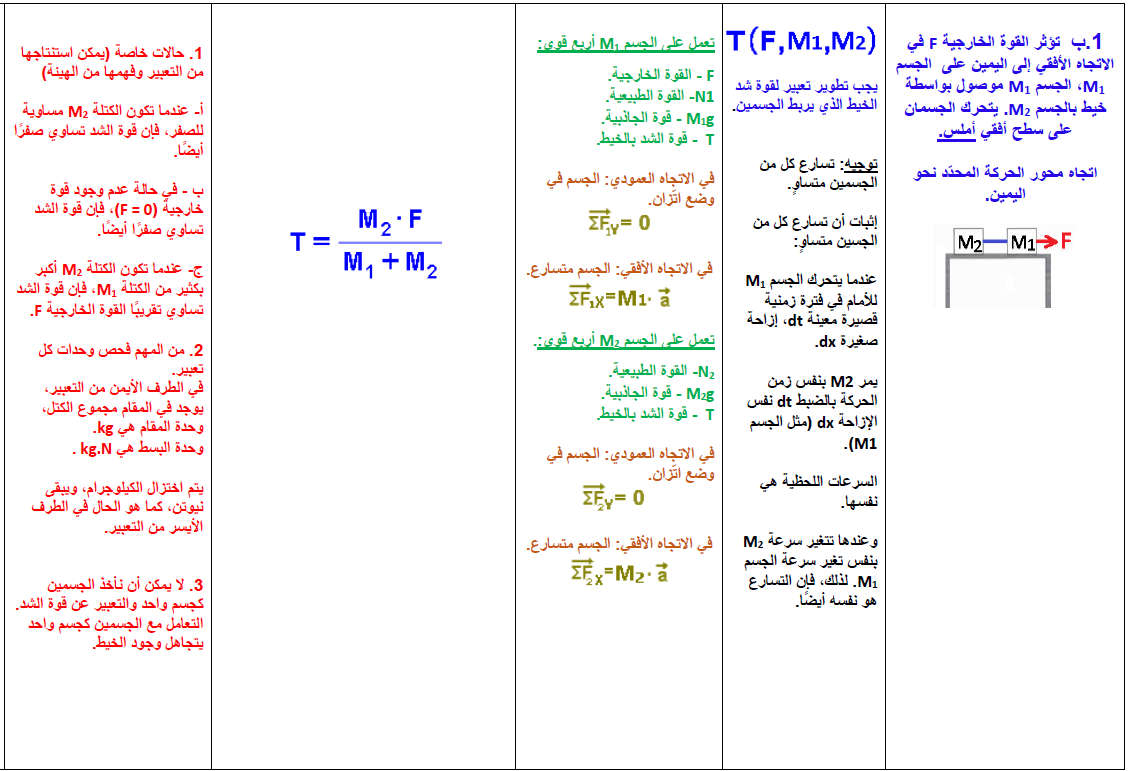
1.1. التسارع بتأثير قوة أفقية
يتحرك كلا الجسمين على سطح أفقي أملس.
تعمل أربع قوى على الجسم الأيمن M1: قوة خارجية F لجهة اليمين، وقوة التوتر T، وقوة الجاذبية W1 والقوة العمودية N1.
نرسم مخطط القوى المؤثرة على M1:
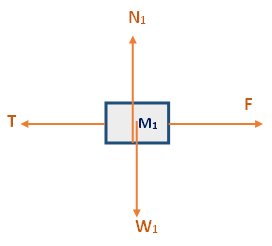
نحدّد المحور X في اتجاه أفقي نحو اليمين والمحور Y عموديًا لأعلى.
في الاتجاه العمودي y يكون الجسم في وضع اتّزان، نكتب معادلات الحركة في الاتجاه العمودي:
في الاتجاه الأفقي X ، الجسم M1 ليس في وضع اتّزان، نكتب معادلة الحركة في الاتجاه الأفقي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
تعمل ثلاث قوى على الجسم الأيسر M2: قوة الشد T وقوة الجاذبية W2 والقوة العمودية N2.
نرسم مخطط القوى التي تعمل على الجسم:
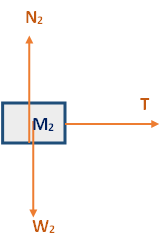
نقوم بضبط المحور X أفقيًا على اليمين والمحور Y عموديًا لأعلى.
الجسم M2 متّزنًا في الاتجاه العمودي، نكتب معادلات الحركة في اتجاه المحور Y:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»N«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/math»
الجسمان موصولان بواسطة خيط لا يتغير طوله، لذا فإن حركتهما هي نفسها. نظرًا لذلك، يمكننا القول أن تسارعهما هو نفسه.
في الاتجاه الأفقي، لا يكون الجسم في وضع اتّزان بل يكون متسارعًا، نكتب معادلات الحركة في اتجاه المحور X:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«/math»
سنقارن بين تعبيري التوتر ونعبر عن التسارع:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mi mathvariant=¨bold¨»F«/mi»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/menclose»«/math»
طريقة اخرى:
يمكن التعامل مع الجسمين كجسم واحد لأنه لا توجد حركة نسبية بينهما ويتحرك كلاهما معًا بنفس السرعة.
تعمل على هيئة الجسمين قوة محصّلة مقدارها F إلى اليمين، الجسمان ليسا في وضع اتّزان، نكتب معادلة الحركة لهيئة الجسمين معًا في اتجاه أفقي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«munder mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»§#8721;«/mo»«mrow/»«/munder»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ largeop=¨true¨»M«/mo»«mi mathcolor=¨#0000FF¨ mathvariant=¨bold¨»t«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mi mathvariant=¨bold¨»F«/mi»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/menclose»«/math»
1.2. قوة التوتربالخيط الذي يربط بين الجسمين
نستخدم تعبير التوتر من القسم السابق:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«/math»
نعوّض تعبير التسارع الذي وجدناه:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»F«/mi»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»F«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/menclose»«/math»
2. جسمان يتحركان على سطح أفقي غير أملس


2.1. التسارع تحت تأثير قوة خارجية أفقية
يتحرك الجسمان على سطح أفقي بمعامل احتكاك μk.
تعمل خمس قوى على الجسم الأيمن M1: القوة الخارجية F ، قوة الاحتكاك fk1 ، قوة الشد T ، قوة الجاذبية W1 والقوة العمودية N1.
نرسم مخططًا للقوى المؤثرة على الجسم 1:
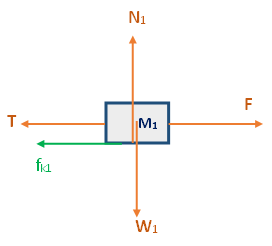
نحدّد المحور X باتجاه أفقي نحو اليمين والمحور Y عموديًا لأعلى.
الجسم M1 متّزنًا في الاتجاه العمودي، نكتب معادلات الحركة في اتجاه المحور Y:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»N«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mspace linebreak=¨newline¨/»«/math»
نستخدم تعبير الاحتكاك الحركي للتعبير عن قوة الاحتكاك المؤثرة على الجسم 1:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»k«/mi»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»f«/mi»«mrow»«mi mathvariant=¨bold¨»k«/mi»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/math»
الجسم M1 ليس متّزنًا في الاتجاه الأفقي، نكتب معادلات الحركة في الاتجاه المحور X:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»k«/mi»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mfenced mathcolor=¨#0000FF¨»«mn»1«/mn»«/mfenced»«mspace linebreak=¨newline¨/»«/math»
تعمل أربع قوى على الجسم الأيسر M2: قوة الشد T وقوة الاحتكاك fk2 وقوة الجاذبية W2 والقوة العمودية N2.
نرسم مخطّط القوى التي تعمل على الجسم 2:
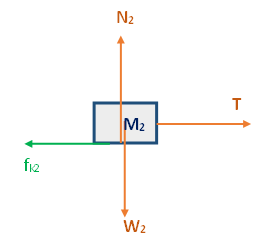
الجسم M2 متّزنًا بالاتجاه العمودي، نكتب معادلات الحركة في اتجاه المحور Y:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»N«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/math»
نستخدم تعبير الاحتكاك الحركي للتعبير عن قوة الاحتكاك المؤثرة على الجسم 2:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»k«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»f«/mi»«mrow»«mi mathvariant=¨bold¨»k«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/math»
يتحرك الجسمان في الاتجاه الأفقي بتسارع. الجسمان موصولان بواسطة خيط لا يتغير طوله ، لذا لهما نفس الحركة. نظرًا لذلك، يمكننا القول أن لهما نفس مقدارالتسارع أيضًا.
نكتب معادلات الحركة للجسم 2 في اتجاه المحور X :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»k«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mfenced mathcolor=¨#0000FF¨»«mn»2«/mn»«/mfenced»«/math»
نقارن بين التعبيرين 1 و 2 للتوتر ونعبر عن التسارع a:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/menclose»«/math»
طريقة أخرى:
يمكن التعامل مع الجسمين كجسم واحد لأنه لا توجد حركة نسبية بينهما ويتحرك كلاهما معًا بنفس السرعة.
في هيئة الجسمين، تعمل القوة F في الاتجاه الأفقي لجهة اليمين، وقوتا الاحتكاك نحو اليسار في اتجاه الحركة.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨14px¨»«munder mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»§#8721;«/mo»«mrow/»«/munder»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»M«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«/msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«msub»«mo largeop=¨true¨ mathvariant=¨bold¨»f«/mo»«mrow»«mi mathvariant=¨bold¨»k«/mi»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mo largeop=¨true¨ mathvariant=¨bold¨»f«/mo»«mrow»«mi mathvariant=¨bold¨»k«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«msub»«mo largeop=¨true¨ mathvariant=¨bold¨»M«/mo»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mo largeop=¨true¨ mathvariant=¨bold¨»M«/mo»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ largeop=¨true¨»a«/mo»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«msub»«mo largeop=¨true¨ mathvariant=¨bold¨»§#956;«/mo»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mo largeop=¨true¨ mathvariant=¨bold¨»M«/mo»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mo largeop=¨true¨ mathvariant=¨bold¨»g«/mo»«mrow/»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mo largeop=¨true¨ mathvariant=¨bold¨»§#956;«/mo»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mo largeop=¨true¨ mathvariant=¨bold¨»M«/mo»«mn mathvariant=¨bold¨»2«/mn»«/msub»«msub»«mo largeop=¨true¨ mathvariant=¨bold¨»g«/mo»«mrow/»«/msub»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«msub»«mo largeop=¨true¨ mathvariant=¨bold¨»M«/mo»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mo largeop=¨true¨ mathvariant=¨bold¨»M«/mo»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ largeop=¨true¨»a«/mo»«/mstyle»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/menclose»«/mstyle»«/math»
2.2. شد الخيط بين جسمين مع الاحتكاك
نستخدم تعبير التوتر الذي وجدناه في القسم السابق:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«/math»
نعوّض تعبير التسارع الذي وجدناه:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»F«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/menclose»«/math»
3. قوة تعمل بزاوية


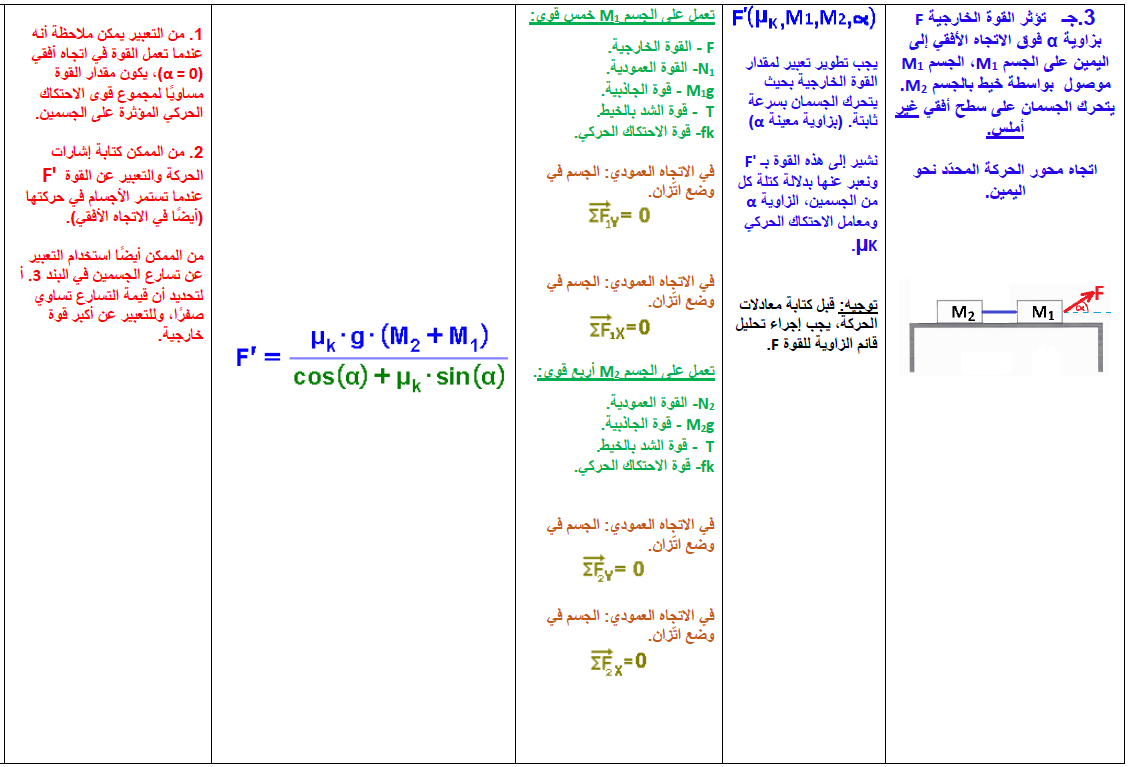
3.1. جسمان موصولان على سطح أفقي غير أملس
يتحرك الجسمان على سطح أفقي بمعامل احتكاك kμ.
تعمل خمس قوى على الجسم الأيمن 1M: القوة الخارجية F ، قوة الاحتكاك k1f ، قوة الشد T ، قوة الجاذبية 1W والقوة العمودية 1N.
نرسم مخططًا للقوى المؤثرة على الجسم 1:
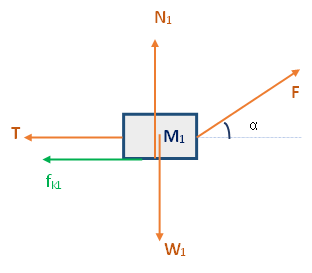
نحدّد المحور X باتجاه أفقي نحو اليمين والمحور Y عموديًا لأعلى.
نحلل تحليلًا قائم الزاوية للقوة الخارجية F:
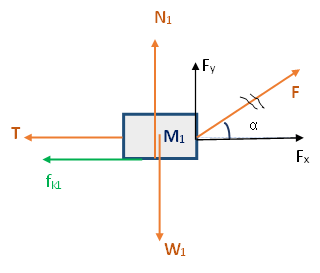
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Fcos«/mi»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨»«mo stretchy=¨true¨»(«/mo»«mi»§#945;«/mi»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Fsin«/mi»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨»«mo stretchy=¨true¨»(«/mo»«mi»§#945;«/mi»«mo stretchy=¨true¨»)«/mo»«/mstyle»«/math»
الجسم متّزنًا في الاتجاه العمودي، نكتب معادلات الحركة في اتجاه المحور Y:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Fsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»N«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»Fsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«mspace linebreak=¨newline¨/»«/math»
نعبر عن قوة الاحتكاك المؤثرة على الجسم 1:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»k«/mi»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»f«/mi»«mrow»«mi mathvariant=¨bold¨»k«/mi»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»Fsin«/mi»«mrow»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«/math»
الجسم M1 ليس متّزنًا في الاتجاه الأفقي، نكتب معادلات الحركة في الاتجاه المحور X:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»k«/mi»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Fcos«/mi»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Fsin«/mi»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»Fcos«/mi»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»Fsin«/mi»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mfenced mathcolor=¨#0000FF¨»«mn»1«/mn»«/mfenced»«mspace linebreak=¨newline¨/»«/math»
تعمل أربع قوى على الجسم الأيسر M2 : قوة التوتر T، قوة الاحتكاك fk2، قوة الجاذبية W2 والقوة العمودية N2.
نرسم مخطّط القوى التي تعمل على الجسم 2:
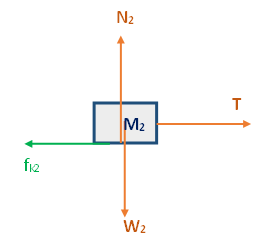
الجسم M2 متّزنًا بالاتجاه العمودي، نكتب معادلات الحركة في اتجاه المحور Y :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»N«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/math»
نستخدم تعبير الاحتكاك الحركي للتعبير عن قوة الاحتكاك المؤثرة على الجسم 2:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»k«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»f«/mi»«mrow»«mi mathvariant=¨bold¨»k«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/math»
يتحرك الجسمان في الاتجاه الأفقي بتسارع. الجسمان موصولان بواسطة خيط لا يتغير طوله، لذا فلهما نفس الحركة. نظرًا لذلك، يمكننا القول أن تسارع كل من الجسمين متساوٍ.
نكتب معادلات الحركة للجسم 2 في اتجاه المحور X:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»k«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mfenced mathcolor=¨#0000FF¨»«mn»2«/mn»«/mfenced»«/math»
نجمع التعبيرين 1 و 2 للتوتر ونعبر عن التسارع a:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Fcos«/mi»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Fsin«/mi»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»Fcos«/mi»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»Fsin«/mi»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/menclose»«/math»
3.2. التوتربالخيط الواصل بين جسمين على سطح أفقي غير أملس
نستخدم المعادلة التي طوّرناها بالبند السابق ونعوّض فيه التسارع الذي وجدناه :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»Fcos«/mi»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»Fsin«/mi»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»Fcos«/mi»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»Fsin«/mi»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»Fcos«/mi»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»Fsin«/mi»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»sin«/mi»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/menclose»«/math»
3.3. ايجاد القوة الخارجية
نستخدم تعبير التسارع من البند ج في حالة تحرك الجسم بسرعة ثابتة (a=0):«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»Fcos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»Fsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»`«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»`«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»`«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»Fsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«/menclose»«/math»
4. جسمان معلقان بواسطة بكرة
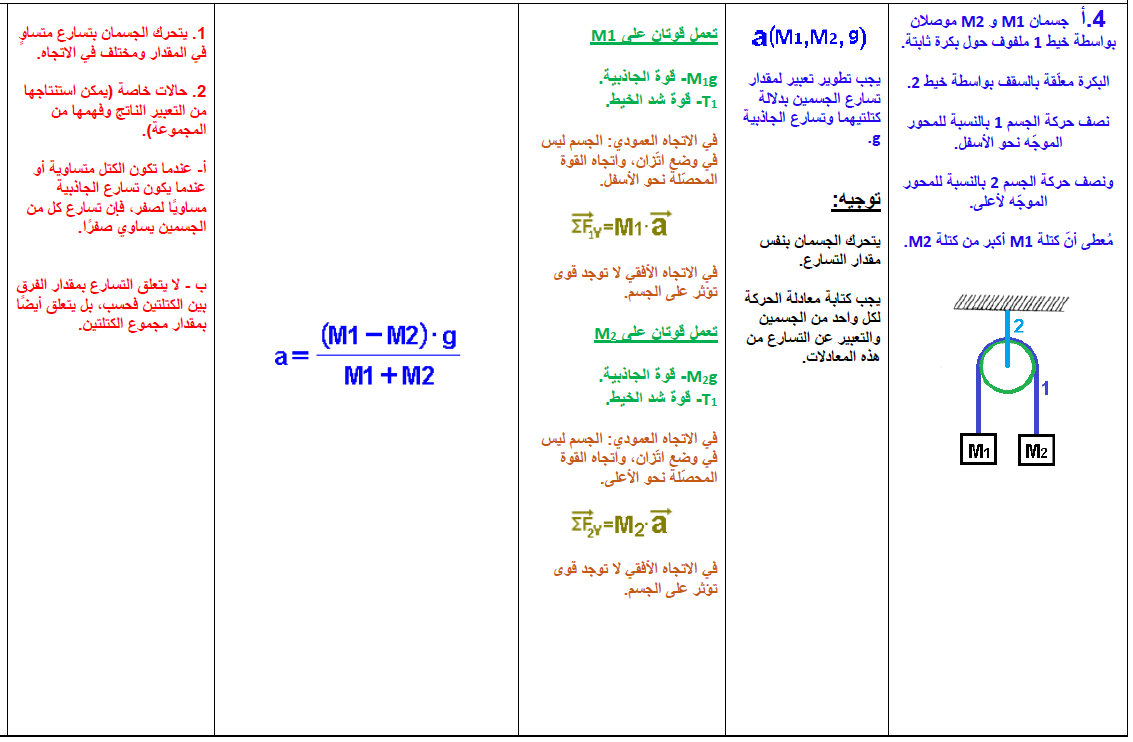
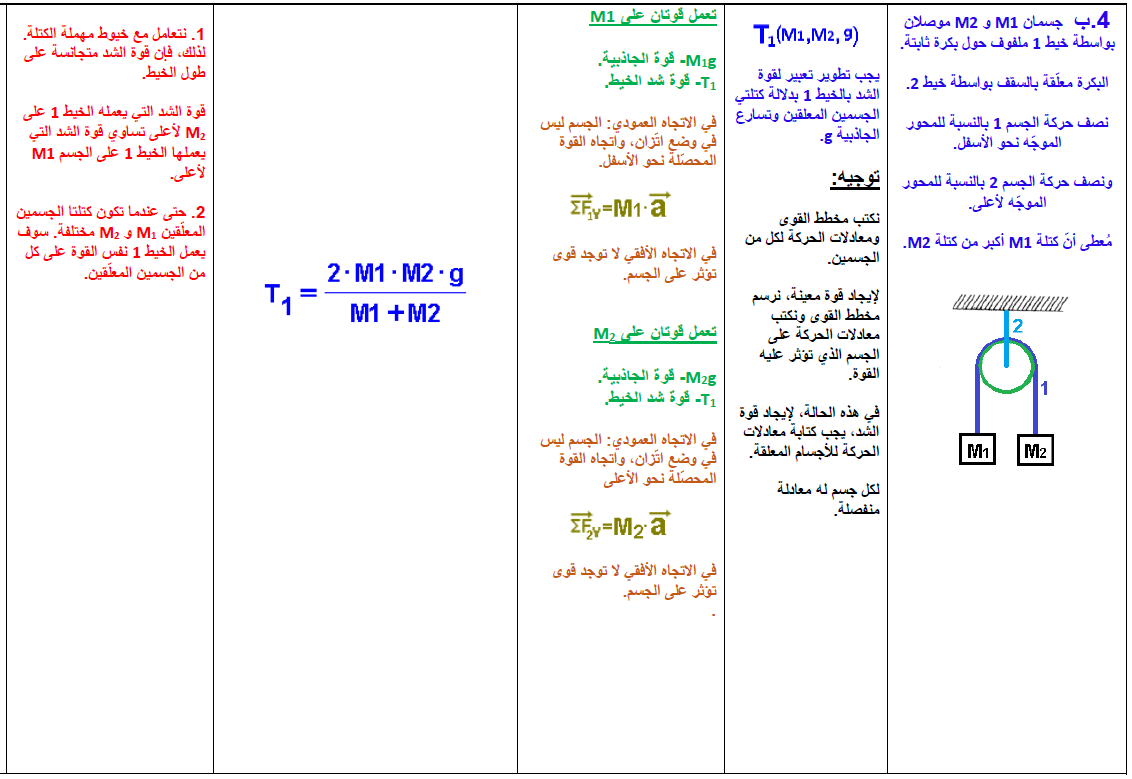
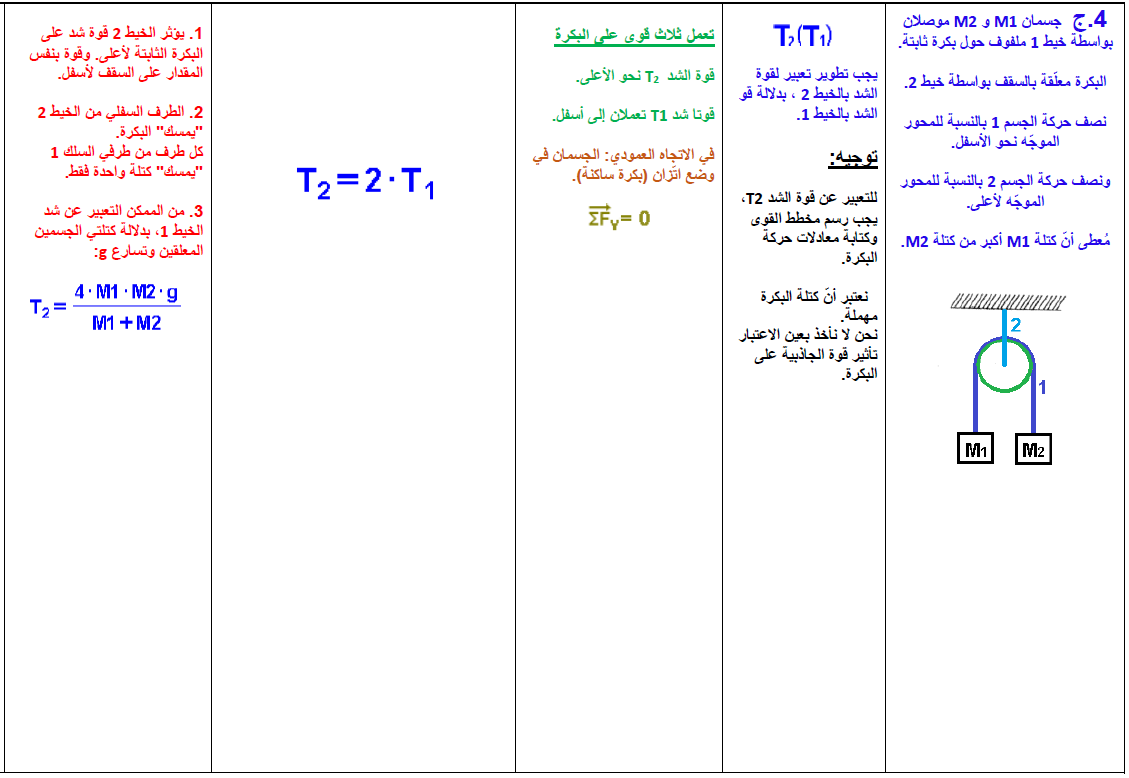
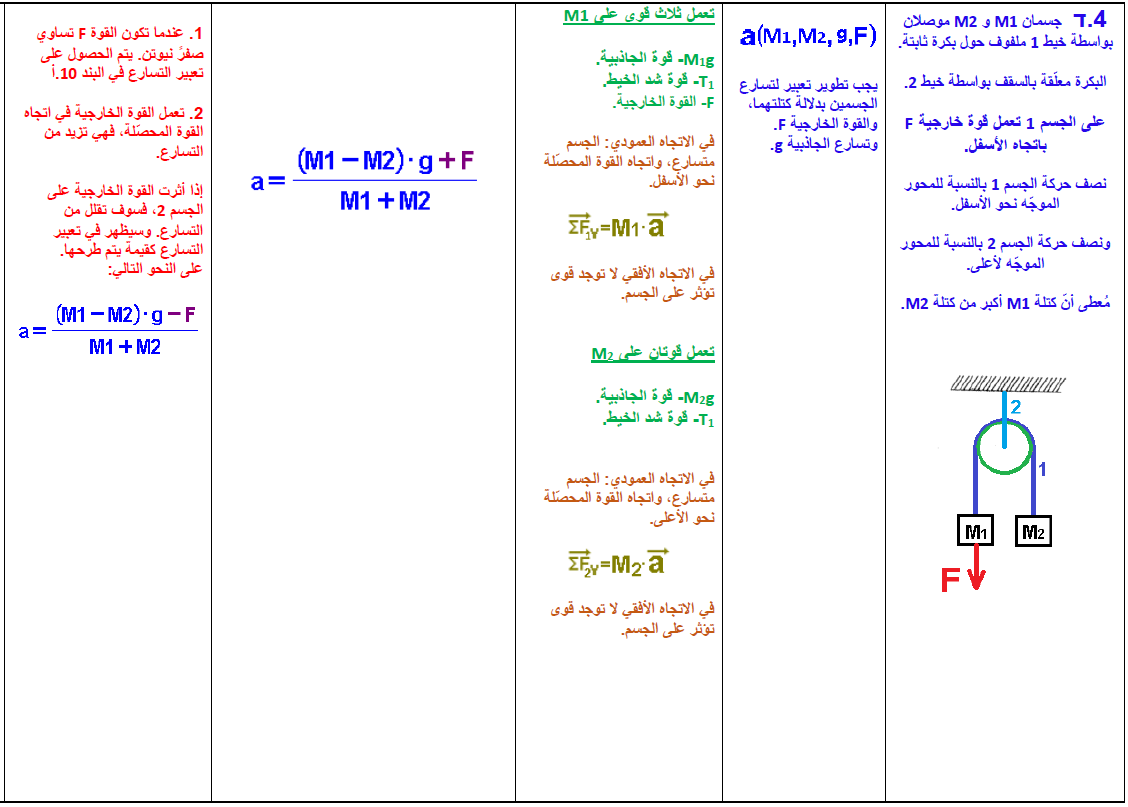
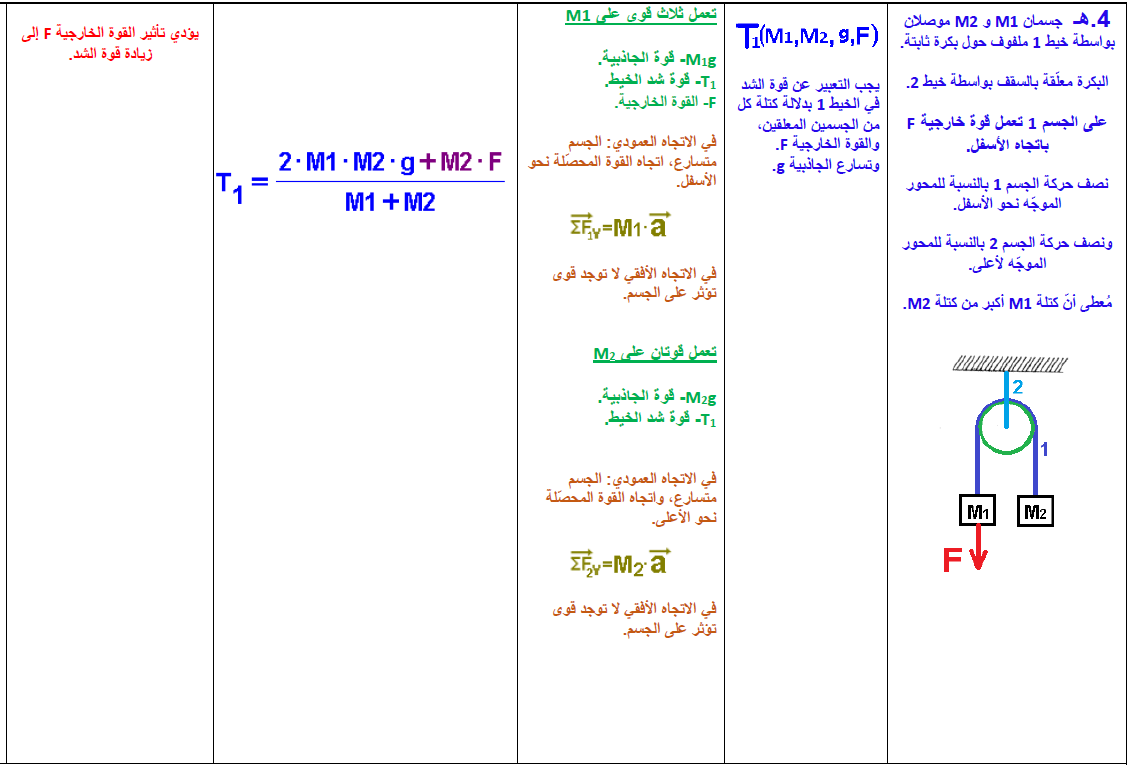

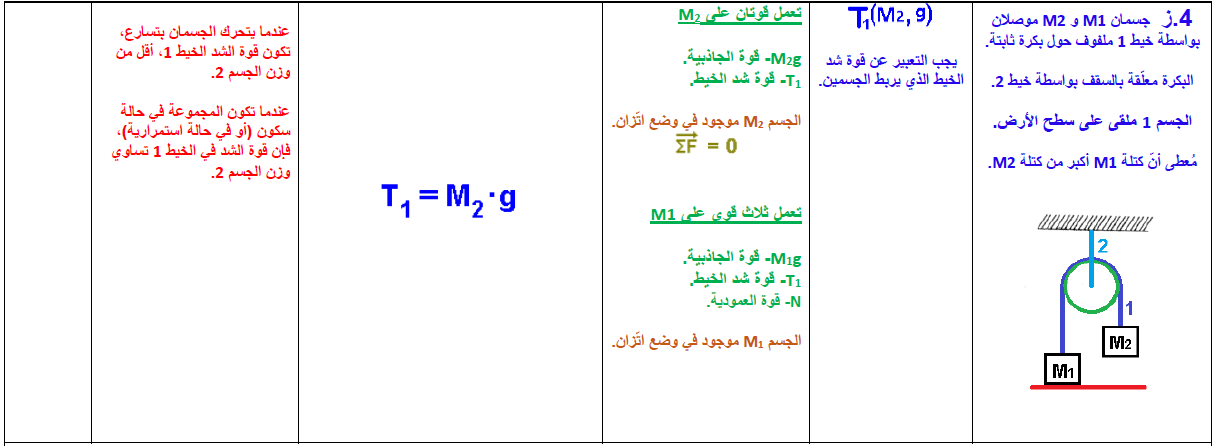
4.1. تسارع الجسمين
جسمان موصلان بخيط يتحركان عموديًا في اتجاهين متعاكسين.
لضمان أن يكون لتسارع كل منهما نفس الإشارة، نقوم باختيار المحور Y للجسم 1 لأسفل والمحور Y للجسم 2 لأعلى.
تؤثر قوتان على كل جسم: قوة الجاذبية W وقوة التوتر T1.
(من المهم أن نتذكر أن قوة الشد هي نفسها في كلا الطرفين، على الرغم من أن الخيط يمر حول البكرة - عندما يتم إهمال قوى الاحتكاك بين الخيط والبكرة وعندما يتم إهمال كتلة الخيط).
نرسم مخططًا للقوى المؤثرة على الجسم 1:
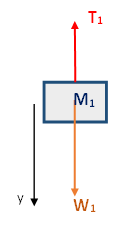
نكتب معادلات الحركة للجسم 1 باتجاه المحور :Y
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»T«/mi»«mn»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mfenced mathcolor=¨#0000FF¨»«mn»1«/mn»«/mfenced»«mspace linebreak=¨newline¨/»«/math»
نرسم مخطّط القوى التي تعمل على الجسم 2:
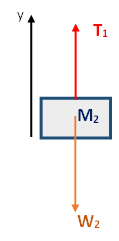
نكتب معادلات الحركة للجسم 2 باتجاه المحور :Y
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#00007F¨»T«/mi»«mn mathcolor=¨#00007F¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mfenced mathcolor=¨#0000FF¨»«mn»2«/mn»«/mfenced»«/math»
نجمع التعبيرين 1 و 2 للتوتر ونعبر عن التسارع :a
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/menclose»«/math»
4.2. قوة الشد بالخيط بين الجسمين
نستخدم إحدى المعادلات المشار لها في القسم السابق:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«/math»
نعوّض التسارع الذي وجدناه ونعبر عن قوة الشد T:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/menclose»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/menclose»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/menclose»«/math»
4.3. قوة الشد بالخيط بين البكرة والسقف
نتطرق إلى القوى المؤثرة على البكرة (مهملة الكتلة).
تعمل ثلاث قوى على البكرة: قوة الشد T على كلا الجانبين ، وقوة الشد T2 التي يُشغلها الخيط المربوط بالسقف.
نرسم مخططًا للقوى المؤثرة على البكرة:
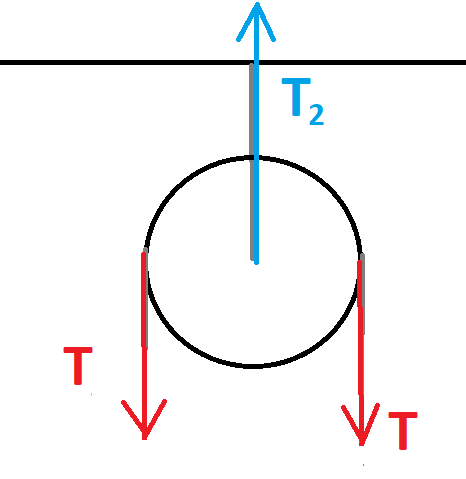
البكرة في حالة سكون. لنكتب معادلة الحركة في اتجاه المحور العمودي للبكرة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mrow/»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»2«/mn»«msub»«mi mathvariant=¨bold¨»T«/mi»«mrow/»«/msub»«/menclose»«/math»
4.4. التسارع تحت تأثير قوة خارجية
جسمان موصلان بخيط يتحركان عموديًا في اتجاهين متعاكسين.
لضمان أن يكون لتسارع كل منهما نفس الإشارة، سنقوم بتحديد المحور Y للجسم 1 لأسفل والمحور Y للجسم 2 لأعلى.
تعمل على الجسم 1 ثلاث قوى: قوة خارجية F وقوة الجاذبية W1 وقوة التوتر T1.
نرسم مخططًا للقوى المؤثرة على الجسم 1:
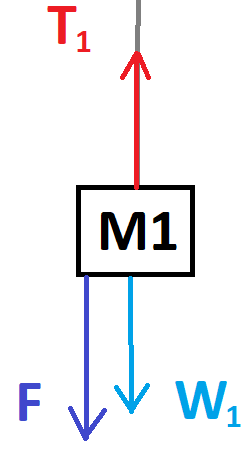
نكتب معادلات الحركة في المحور Y الذي تم اختيار اتجاهه إلى الأسفل :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo mathcolor=¨#00007F¨»§#160;«/mo»«mo mathcolor=¨#00007F¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mfenced mathcolor=¨#0000FF¨»«mn»1«/mn»«/mfenced»«mspace linebreak=¨newline¨/»«/math»
تؤثر قوتان على الجسم 2: قوة الجاذبية W2 وقوة التوتر T1.
نرسم مخطّط القوى التي تعمل على الجسم 2:
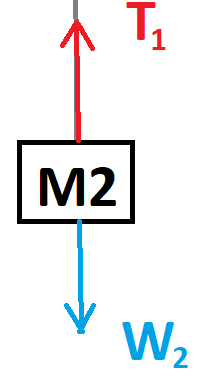
نكتب معادلات الحركة في المحور Y الذي تم اختيار اتجاهه نحو الأعلى :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mfenced mathcolor=¨#0000FF¨»«mn»2«/mn»«/mfenced»«/math»
نجمع التعبيرين 1 و 2 المشار لهما ونعبر عن التسارع a:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»F«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/menclose»«/math»
4.5. قوة شد الخيط بين الجسمين
نستخدم إحدى المعادلات المشار لها في القسم السابق:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«/math»
نعوض تعبير التسارع الذي وجدناه:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mrow»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»F«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/menclose»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/menclose»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»F«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»F«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/menclose»«/math»
4.6. القوة العمودية
كلا الجسمين في حالة سكون، وفقًا للقانون الأول لنيوتن.
تعمل ثلاث قوى على الجسم 1: قوة الجاذبية W1 ، والقوة العمودية N وقوة التوتر T1.
نرسم مخططًا للقوى المؤثرة على الجسم 1:
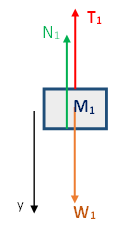
نكتب معادلات الحركة للجسم 1:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»N«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«/menclose»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mfenced mathcolor=¨#0000FF¨»«mn»1«/mn»«/mfenced»«mspace linebreak=¨newline¨/»«/math»
تؤثر قوتان على الجسم 2: قوة الجاذبية W2 وقوة التوتر T1.
نكتب معادلات الحركة للجسم 1:
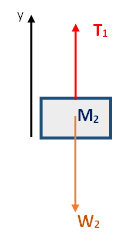
نكتب معادلات الحركة للجسم 2:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«/menclose»«mo»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mfenced mathcolor=¨#0000FF¨»«mn»2«/mn»«/mfenced»«/math»
نقوم بجمع المعادلتين المشار لهما ونعبر عن N1:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»N«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/math»
4.7. قوة التوتر بين الجسمين في حالة السكون
نستخدم إحدى المعادلتين المشار لهما من القسم السابق:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/math»
5. جسم معلق وجسم آخر على سطح أفقي أملس
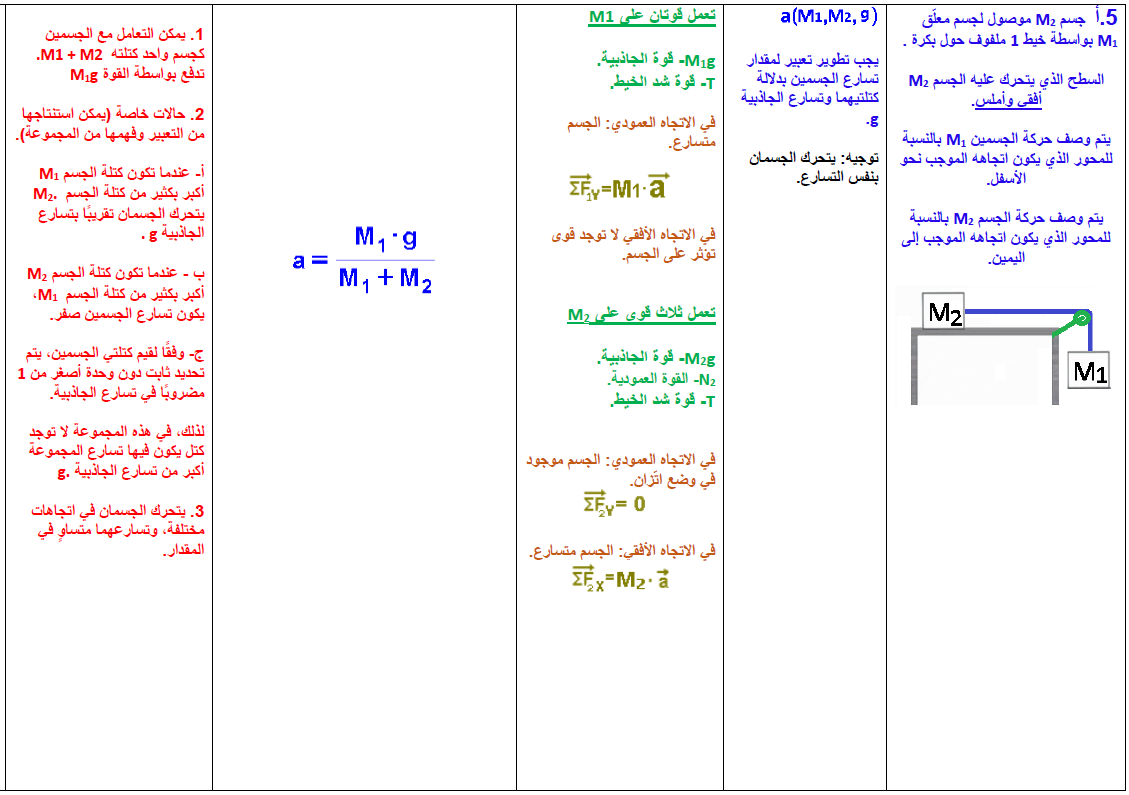
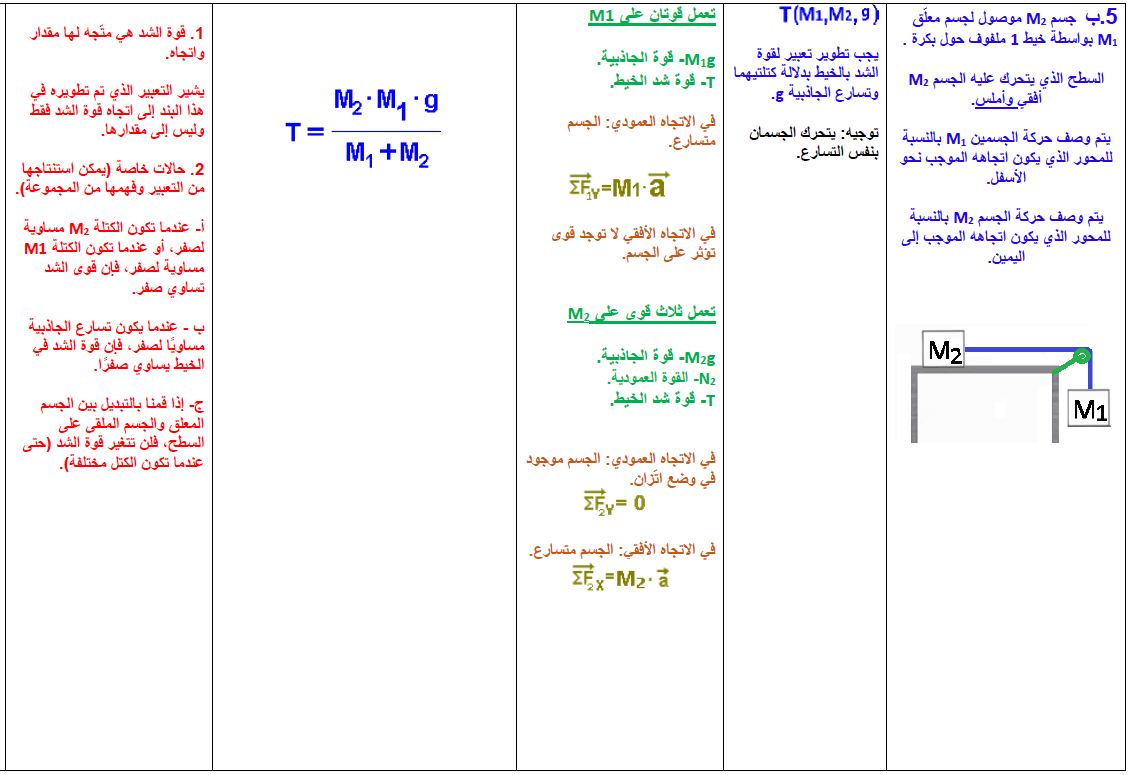
5.1. التسارع
يتحرك الجسم 1 بتسارع نحو الأسفل والجسم 2 يتحرك على سطح أفقي أملس بتسارع نحو اليمين.
الجسمان موصولان بواسطة خيط مهمل الكتلة، وبالتالي فهما يتحركان بنفس مقدار التسارع.
لضمان أن يكون لتسارع كل منهما نفس الإشارة، نقوم بتعيين المحور Y للجسم 1 لأسفل ، والمحور X للجسم 2 نحو اليمين.
تؤثر قوتان على الجسم 1: قوة الجاذبية W1 وقوة التوتر T.
نرسم مخططًا للقوى المؤثرة على الجسم 1:
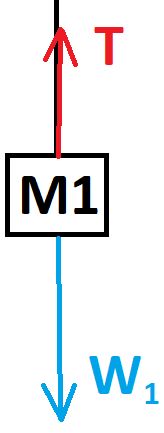
نكتب معادلات الحركة للجسم 1 في اتجاه المحورY نحو الأسفل:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mfenced mathcolor=¨#0000FF¨»«mn»1«/mn»«/mfenced»«mspace linebreak=¨newline¨/»«/math»
تعمل ثلاث قوى على الجسم 2: قوة الشد T وقوة الجاذبية W2 والقوة العمودية N2.
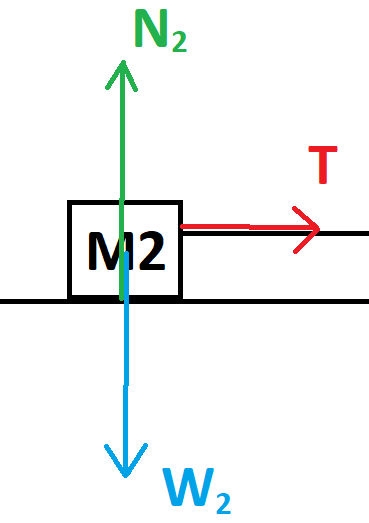
يتحرك الجسم 2 بنفس تسارع الجسم 1 في الاتجاه الأفقي، ونكتب معادلة الحركة بالنسبة للمحور x الذي تم اختياره إلى اليمين.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mfenced mathcolor=¨#0000FF¨»«mn»2«/mn»«/mfenced»«/math»
نعوّض التعبير أعلاه عن T في المعادلة 1 ، ونحصل على:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/menclose»«/math»
5.2. التوتر في الخيط
نستخدم تعبير التوتر من القسم السابق:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«/math»
نعوَض تعبير التسارع الذي وجدناه:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/menclose»«/math»
6. جسم معلق وجسم آخر على سطح أفقي غير أملس
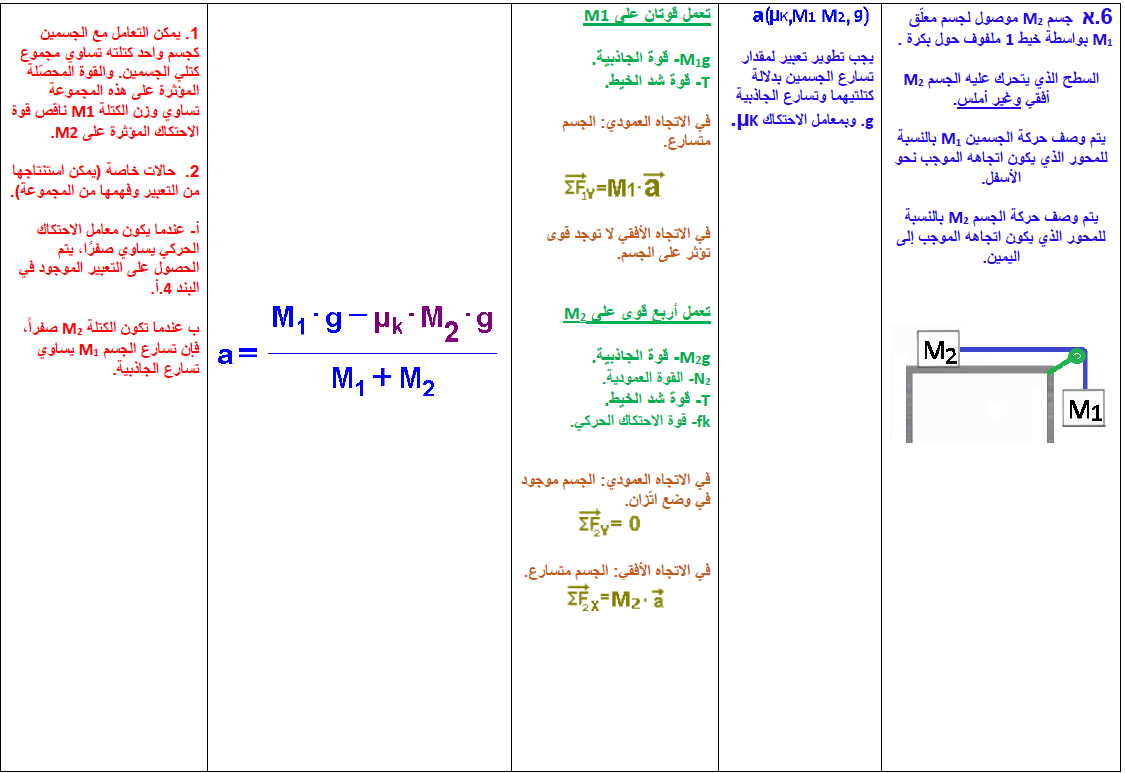
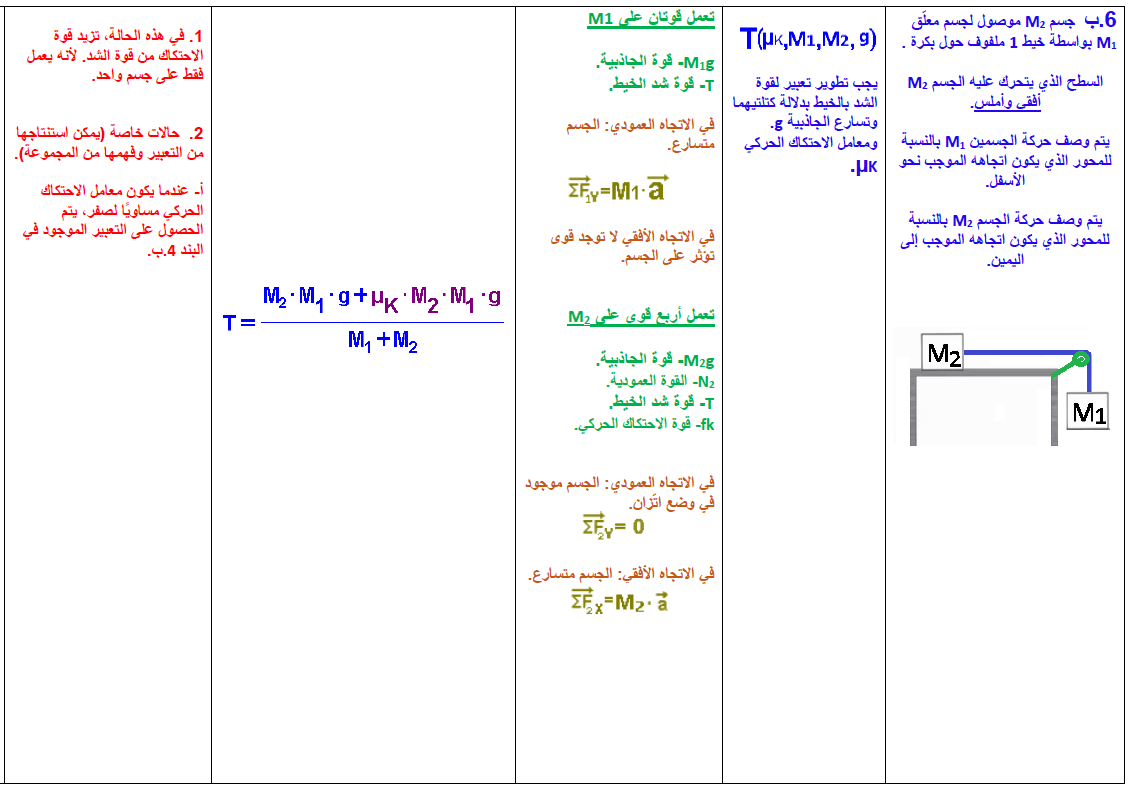
6.1. ايجاد التسارع
يتحرك الجسم 1 بتسارع نحو الأسفل والجسم 2 يتحرك على سطح أفقي أملس بتسارع نحو اليمين.
الجسمان موصولان بواسطة خيط مهمل الكتلة، وبالتالي فهما يتحركان بنفس مقدار التسارع.
لضمان أن يكون لتسارع كل منهما نفس الإشارة، نقوم بتعيين المحور Y للجسم 1 لأسفل ، والمحور X للجسم 2 نحو اليمين.
تؤثر قوتان على الجسم 1: قوة الجاذبية W1 وقوة التوتر T.
نرسم مخططًا للقوى المؤثرة على الجسم 1:
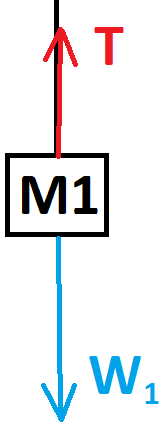
نكتب معادلات الحركة للجسم 1 بالنسبة إلى المحور y الموجب الذي تم اختياره لأسفل.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mfenced mathcolor=¨#0000FF¨»«mn»1«/mn»«/mfenced»«mspace linebreak=¨newline¨/»«/math»
تعمل أربع قوى على الجسم 2: قوة الجاذبية W2، والقوة العمودية N، وقوة التوتر T وقوة الاحتكاك fk.
نرسم مخطّط القوى التي تعمل على الجسم 2:
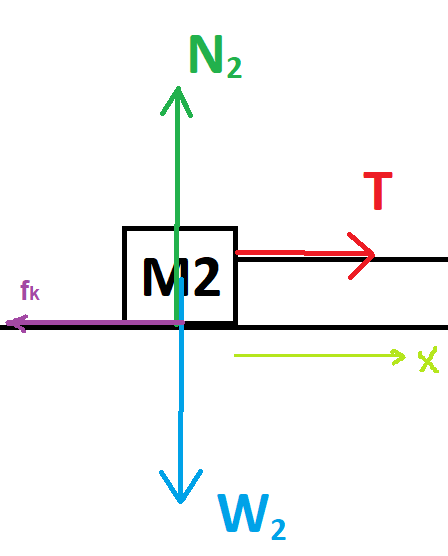
في اتجاه المحور Y ، يكون الجسم 2 في حالة سكون. القانون الأول لنيوتن.
في اتجاه المحور X ، يتحرك الجسم 2 بتسارع مقداره a.
نكتب معادلات الحركة
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»N«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»N«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mfenced mathcolor=¨#0000FF¨»«mn»2«/mn»«/mfenced»«/math»
نجمع المعادلتين المشار لهما أعلاه :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mrow mathcolor=¨#0000FF¨»«mtable columnalign=¨right¨»«mtr»«mtd»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/mtd»«/mtr»«mtr»«mtd»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»N«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/mtd»«/mtr»«/mtable»«mo stretchy=¨true¨ mathvariant=¨bold¨»}«/mo»«/mrow»«mo»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/menclose»«/math»
6.2. ايجاد قوة الشد بالخيط
نستخدم أحدى المعادلتين المشار لهما في البند السابق:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«/math»
نعوّض التعبير للقوة العمودية والتسارع:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msup»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msup»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msup»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/menclose»«/math»
7. قوة خارجية تؤثر على الخيط
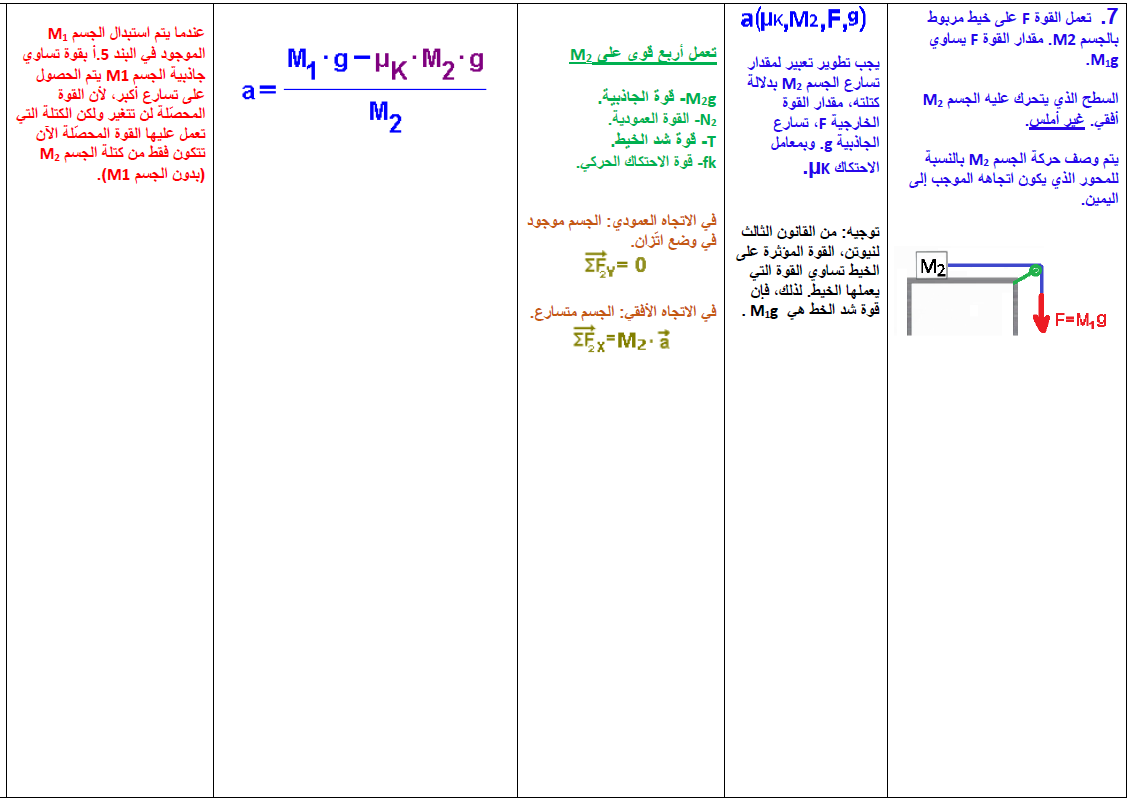
7.1. قوة خارجية تعمل على الخيط
من القانون الثالث لنيوتن، القوة المؤثرة على الخيط تساوي القوة التي يُشغلها الخيط ، لذلك يمكننا القول إن قوةشد الخيط هي M1g.
T = M1g
4 قوى تؤثر على الجسم 2: قوة الشد T وقوة الاحتكاك fk وقوة الجاذبية W2 والقوة العمودية N.
لنرسم مخططًا للقوى المؤثرة على الجسم 2:
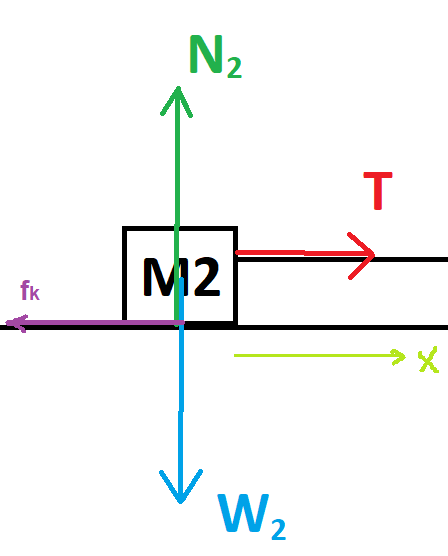
نكتب معادلات الحركة للجسم 2 :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»N«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«/menclose»«/math»
8. جسم معلق وجسم آخرعلى سطح مائل أملس


8.1. ايجاد التسارع
يتحرك الجسم 1 عموديًا بينما يتحرك الجسم 2 على طول السطح المائل.
نظرًا لأن الجسمين موصولين بخيط مثالي مشدود، فإن تسارعهما متساوي المقدار.
لضمان أن يكون لتسارع كل منهما نفس الإشارة، نحدّد المحاور على النحو التالي:
للجسم 1: نختار المحور Y لأسفل.
بالنسبة للجسم 2: نختار المحور X لأعلى السطح المائل والمحور Y العمودي على السطح لأعلى.
تؤثر قوتان على الجسم 1: قوة الجاذبية W1 وقوة التوتر T.
نرسم مخططًا للقوى المؤثرة على الجسم 1:
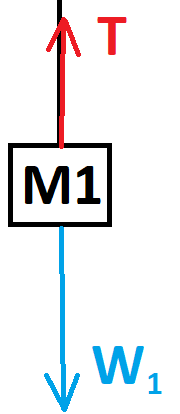
نكتب معادلة الحركة للجسم 1 بالنسبة لمحور y المختار لأسفل.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mfenced mathcolor=¨#0000FF¨»«mn»1«/mn»«/mfenced»«/math»
تؤثر ثلاث قوى على الجسم 2: قوة الشد T وقوة الجاذبية W2 والقوة العمودية N2 .
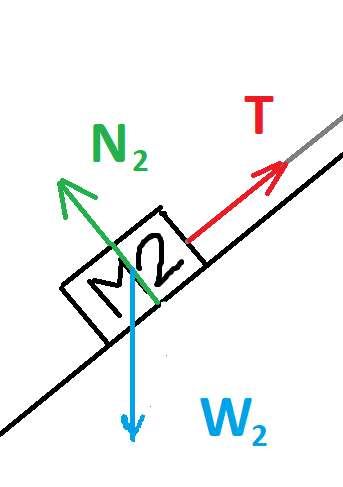
نحلل القوة تحليل قائم الزاوية W2:
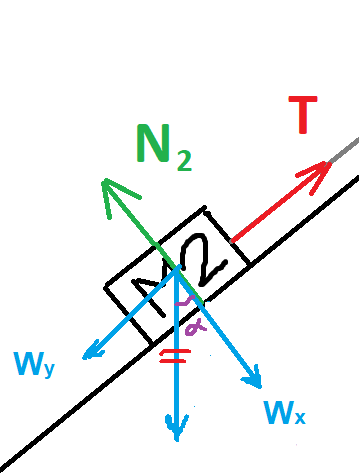
في اتجاه المحور Y ، يكون الجسم 2 في حالة سكون. في اتجاه المحور X ، يتحرك الجسم 2 بتسارع.
نكتب معادلات الحركة 2 في كلا الاتجاهين عموديًا على السطح وباتجاه موازيًا له في اتجاه المحور x الذي تم اختياره:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Wcos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Wsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»N«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mfenced mathcolor=¨#0000FF¨»«mn»2«/mn»«/mfenced»«mspace linebreak=¨newline¨/»«/math»
نجمع معادلتي الحركة 1 و- 2:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/menclose»«/math»
8.2. ايجاد قوة الشد بالخيط
نستخدم المعادلتين اللتين تم تطويرهما في القسم السابق :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«menclose notation=¨updiagonalstrike¨»«msup»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«menclose notation=¨updiagonalstrike¨»«msup»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#8201;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/menclose»«/math»
8.3. ايجاد النسبة بين الكتلتين
إذا كان الجسمان يتحركان بسرعة ثابتة، فهذا يعني أنهما يتحركان بتسارع 0.
سوف نستخدم تعبير التسارع الذي قمنا بتطويره:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»(«/mo»«mi»§#945;«/mi»«mo stretchy=¨true¨»)«/mo»«/mstyle»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/math»
نعوّض في تعبير التسارع a = 0:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»/«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»:«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mfrac»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/math»
9. جسم معلق وجسم آخر معلق على سطح مائل غير أملس


9.1. ايجاد التسارع
يتحرك الجسم 1 عموديًا بينما يتحرك الجسم 2 على طول السطح المائل.
نظرًا لأن الجسمان موصولان بخيط مثالي مشدود ، فإن تسارعهما متساوٍ في المقدار.
لضمان أن يكون لتسارع كل منهما نفس الإشارة،، نحدّد المحاور على النحو التالي:
للجسم 1: نختار المحور Y لأسفل.
بالنسبة للجسم 2: نختار المحور X لأعلى السطح المائل والمحور Y العمودي على السطح لأعلى.
تؤثر قوتان على الجسم 1: قوة الجاذبية W1 وقوة التوتر T.
نرسم مخططًا للقوى المؤثرة على الجسم 1:
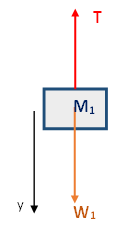
نكتب معادلة الحركة للجسم بالاتجاه العمودي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mfenced mathcolor=¨#0000FF¨»«mn»1«/mn»«/mfenced»«/math»
تعمل أربع قوى على الجسم 2: قوة الجاذبية W2، والقوة العمودية N، وقوة التوتر T وقوة الاحتكاك fk. .
نرسم مخططًا للقوى المؤثرة على الجسم 2:
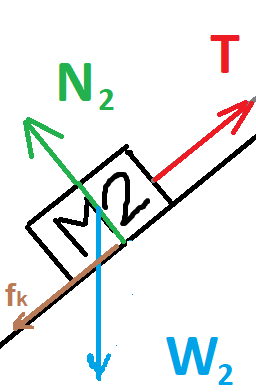
نحلل القوة W2 لمركّبيها:
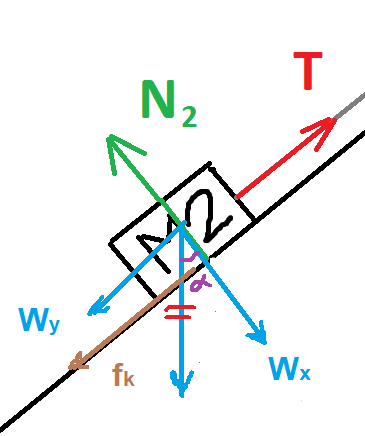
الجسم 2 في حالة سكون في اتجاه المحور Y ويتسارع في اتجاه المحور X.
الجسم 1 يتسارع في اتجاه المحور Y.
نكتب معادلات الحركة للجسم 2 في اتجاه عمودي على المستوى:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gcos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»N«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/math»
نعوّض القوة العمودية في تعبير الاحتكاك الحركي :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mfenced mathcolor=¨#0000FF¨»«mn»2«/mn»«/mfenced»«mspace linebreak=¨newline¨/»«/math»
نجمع المعادلتين المشار لهما ونعبر عن التسارع:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gcos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gcos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/menclose»«/math»
9.2. ايجاد التوتر بالخيط
نستخدم إحدى المعادلتين اللتين تم تطويرهما في القسم السابق من أجل إيجاد قوة الشد:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«/math»
نعوّض مقدار التسارع الذي وجدناه:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«msup»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«menclose notation=¨updiagonalstrike¨»«msup»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/menclose»«/math»
9.3. ايجاد النسبة بين الكتلتين
إذا كان الجسمان يتحركان بسرعة ثابتة، فهذا يعني أنهما يتحركان بتسارع 0.
سوف نستخدم تعبير التسارع الذي قمنا بتطويره:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/math»
نعوّض a = 0:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gcos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»/«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»:«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mfrac»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/math»
10. جسمان على سطحين مائلين




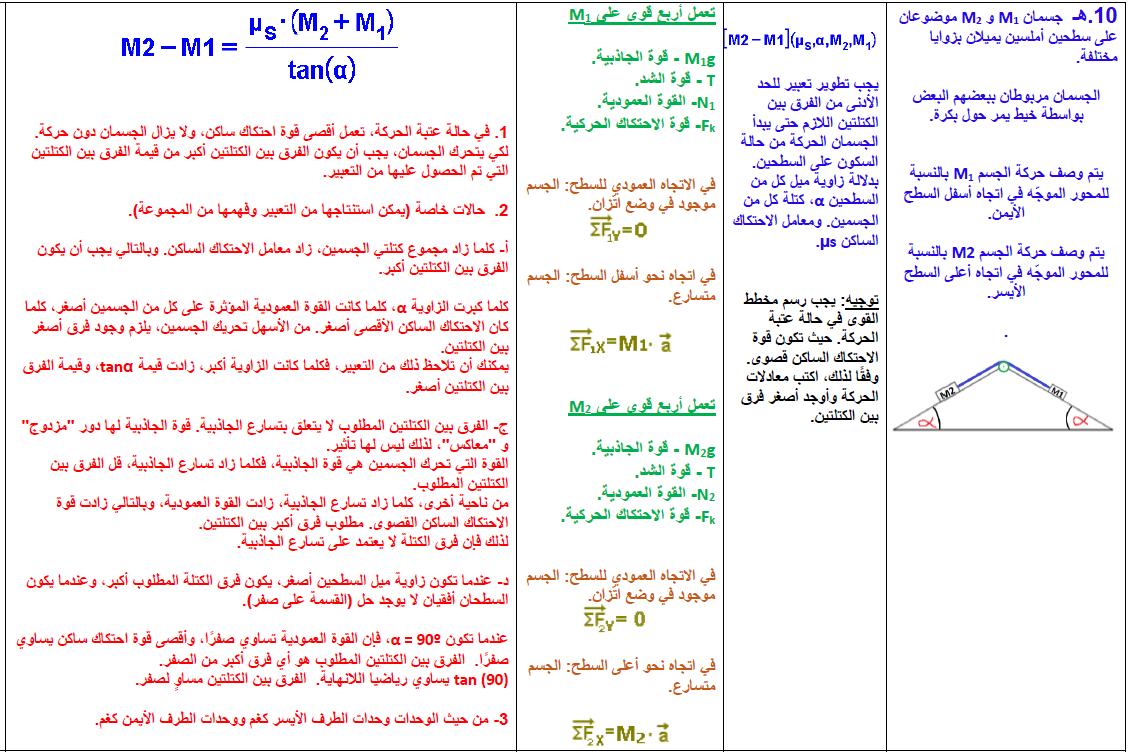
10.1. إيجاد التسارع بدون احتكاك
يتحرك كلا الجسمين على طول السطحين المائلين.
لأن الجسمين موصولين بواسطة خيط مشدود، فإن تسارع كل منهما يكون متساوي المقدار.
لضمان أن يكون لتسارع كل منهما نفس الإشارة، نحدّد المحاور على النحو التالي:
بالنسبة للجسم 1: نقوم بتعيين المحور X لأسفل السطح المائل، والمحور Y متعامد على السطح.
بالنسبة للجسم 2: نحدد المحور X باتجاه السطح المائل لأعلى ، والمحور Y متعامد على السطح.
تعمل ثلاث قوى على الجسم 1: قوة الجاذبية W1 وقوة التوتر T والقوة العمودية N1.
نرسم مخططًا للقوى المؤثرة على الجسم 1:
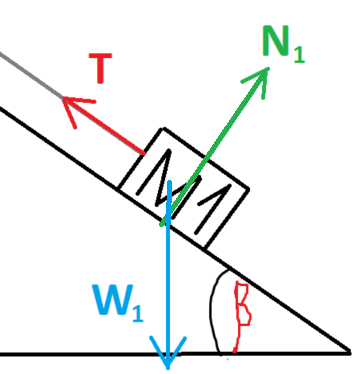
نحلل قوة الجاذبية لمركّبيها:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#946;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gcos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#946;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«/math»
نُشير للتسارع المشترك للجسمين بـ a.
نكتب معادلة الحركة للجسم 1 في اتجاه عمودي على السطح (اتجاه المحور y):
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»N«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«mspace linebreak=¨newline¨/»«/math»
نكتب معادلة الحركة للجسم 1 في اتجاه لأسفل السطح المائل (اتجاه المحور x الذي تم اختياره ليكون المحور الموجب):
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mfenced mathcolor=¨#0000FF¨»«mn»1«/mn»«/mfenced»«mspace linebreak=¨newline¨/»«/math»
تعمل ثلاث قوى على الجسم 2: قوة الجاذبية W2 وقوة الشد T والقوة العمودية N2.
نرسم مخطط القوى التي تعمل على الجسم 2:
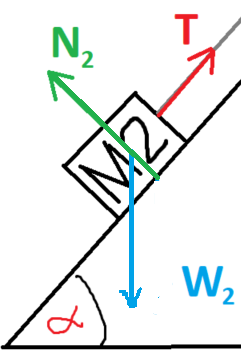
نكتب معادلة الحركة للجسم 2 في اتجاه عمودي على السطح (اتجاه المحور y):
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gcos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»N«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«mspace linebreak=¨newline¨/»«/math»
نكتب معادلة الحركة للجسم 2 في اتجاه نحو أعلى السطح المائل (اتجاه المحور x الذي تم اختياره ليكون المحور الموجب):
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mfenced mathcolor=¨#0000FF¨»«mn»2«/mn»«/mfenced»«/math»
نجمع معادلتي الحركة المشار لهما بـ (1 و 2) ونحصل على:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mrow mathcolor=¨#0000FF¨»«mtable columnalign=¨right¨»«mtr»«mtd»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/mtd»«/mtr»«mtr»«mtd»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/mtd»«/mtr»«/mtable»«mo stretchy=¨true¨ mathvariant=¨bold¨»}«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#946;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#946;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/menclose»«/math»
10.2. ايجاد النسبة بين الكتل
عندما يتحرك الجسمان بسرعة ثابتة، فهذا يعني أن تسارعهما يساوي صفرًا.
نستخدم تعبير التسارع الذي قمنا بتطويره في البند السابق:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/math»
نعوّض a = 0:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#946;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#946;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»/«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»:«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#946;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mfrac»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«/menclose»«/math»
10.3. إيجاد التسارع مع احتكاك
يتحرك كلا الجسمين على طول السطحين المائلين.
لأن الجسمين موصولين بواسطة خيط مشدود، فإن تسارع كل منهما متساوي المقدار.
لضمان أن يكون لتسارع كل منهما نفس الإشارة، نحدّد المحاور على النحو التالي:
بالنسبة للجسم 1: نقوم بتعيين المحور X لأسفل السطح المائل، والمحور Y متعامد على السطح.
بالنسبة للجسم 2: نحدد المحور X باتجاه السطح المائل لأعلى ، والمحور Y متعامد على السطح.
تعمل ثلاث قوى على الجسم 1: قوة الجاذبية W1، قوة الاحتكاك fk1، قوة التوتر T والقوة العمودية N1.
معطى أن الجسمين يتحركان إلى اليمين، وبالتالي فإن الجسم 1 ينزل نحو أسفل السطح المائل، وبالتالي فإن قوة الاحتكاك في اتجاه نحو أعلى السطح المائل (عكس اتجاه الحركة).
نرسم مخططًا للقوى المؤثرة على الجسم 1:
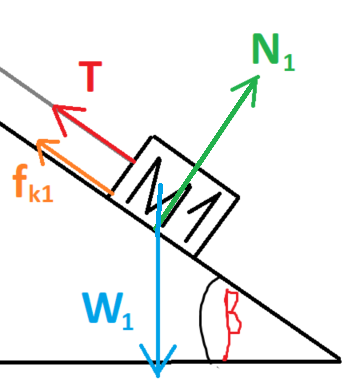
نكتب معادلة الحركة في اتجاه المحور y، العمودي على السطح المائل، والجسم متزنًا في هذا الاتجاه:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gcos«/mi»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»N«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«/menclose»«mspace linebreak=¨newline¨/»«/math»
يتحرك الجسم 1 نحو أسفل السطح المائل بتسارع a ، ونكتب معادلة الحركة لهذا الجسم في اتجاه الحركة (في اتجاه المحور x):
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»k«/mi»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»f«/mi»«mrow»«mi mathvariant=¨bold¨»k«/mi»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»k«/mi»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mfenced mathcolor=¨#0000FF¨»«mn»1«/mn»«/mfenced»«mspace linebreak=¨newline¨/»«/math»
تعمل أربع قوى على الجسم 2: قوة الجاذبية W2، قوة الاحتكاك fk2 ، قوة الشد T والقوة العمودية N2.
يتحرك الجسمان نحو اليمين ، وبالتالي يرتفع الجسم 2 نحو أعلى السطح المائل، وبالتالي فإن قوة الاحتكاك تكون في اتجاه أسفل السطح المائل (عكس اتجاه الحركة).
نرسم مخططًا للقوى المؤثرة على الجسم 2:
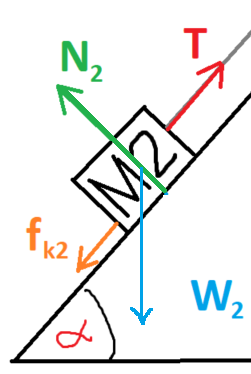
نكتب معادلة الحركة في اتجاه المحور y، وهو عمودي على السطح المائل، والجسم متّزنًا في هذا الاتجاه:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gcos«/mi»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»N«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«/menclose»«mspace linebreak=¨newline¨/»«/math»
يتحرك الجسم 2 نحو أعلى المستوى المائل بالتسارع a ، نكتب معادلة الحركة لهذا الجسم في اتجاه الحركة (في اتجاه المحور x الذي تم اختياره):
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»k«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»k«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gcos«/mi»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mfenced mathcolor=¨#0000FF¨»«mn»2«/mn»«/mfenced»«/math»
نجمع معادلتا الحركة في الاتجاه الأفقي ونحصل:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mrow mathcolor=¨#0000FF¨»«mtable columnalign=¨right¨»«mtr»«mtd»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/mtd»«/mtr»«mtr»«mtd»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/mtd»«/mtr»«/mtable»«mo stretchy=¨true¨ mathvariant=¨bold¨»}«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#946;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gcos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#946;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gcos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#946;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gcos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gcos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#946;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/menclose»«/math»
10.4. إيجاد النسبة بين الكتلتين مع احتكاك
عندما يتحرك الجسمان بسرعة ثابتة، فهذا يعني أن تسارعها يساوي صفرًا.
نستخدم تعبير التسارع الذي قمنا بتطويره في البند السابق:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/math»
نعوّض a = 0:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#946;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gcos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gcos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#946;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#946;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#946;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»/«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»:«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#946;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#946;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mfrac»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#946;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«/menclose»«/math»
10.5. إيجاد فرق الكتلة الأدنى
نتطرق إلى الجسمين كهيئة ساكنة تعمل عليها قوة احتكاك ساكن.
بعد ذلك نجد حد فرق الكتلة الذي يمكّن الهيئة أن تكون في حالة سكون، وبناءً على ذلك نستنتج أقصى فرق بين الكتلتين.
تعمل أربع قوى على الجسم 1: قوة الجاذبية W، وقوة الاحتكاك fs، وقوة الشد T والقوة العمودية N.
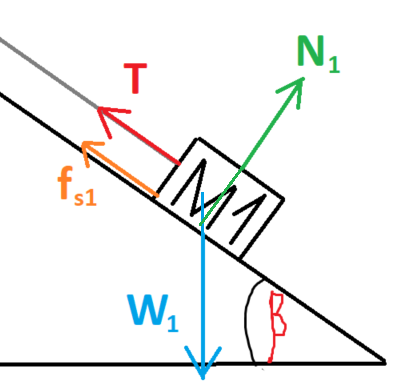
معطى أنّ α = β.
نختيار محور الحركة y في الاتجاه العمودي للسطح المائل أعلاه ومحور الحركة x في اتجاه لأسفل السطح المائل.
نقوم بتحليل قوة الجاذبية إلى مركّبيها.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gcos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«/math»
سنكتب معادلات الحركة في الاتجاه العمودي للسطح (في اتجاه المحور y) ونجد أقصى قوة احتكاك ساكن يمكن أن تعمل على الجسم 1:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»N«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8804;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»f«/mi»«mrow»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#8804;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«mspace linebreak=¨newline¨/»«/math»
نكتب الآن معادلات الحركة في اتجاه أسفل السطح المائل (في اتجاه المحور x الذي تم تحديده) للجسم 1:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»f«/mi»«mrow»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«/menclose»«mspace linebreak=¨newline¨/»«/math»
تعمل أربع قوى على الجسم 2: قوة الجاذبية W، وقوة الاحتكاك fs، وقوة الشد T والقوة العمودية N.
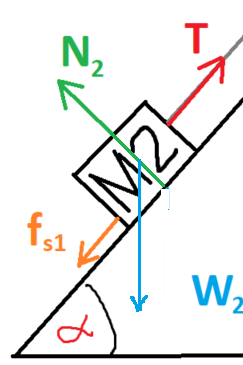
نختار محور الحركة y في الاتجاه العمودي على السطح المائل أعلاه ومحور الحركة x في الاتجاه لأعلى السطح المائل.
ونقوم بتحليل قوة الجاذبية لمركّبيها:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gcos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«/math»
نكتب معادلة الحركة في الاتجاه العمودي للسطح المائل (في اتجاه المحور y) ونجد أقصى قوة احتكاك ساكن يمكن أن تعمل على الجسم 2:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»N«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8804;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»f«/mi»«mrow»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#8804;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«mspace linebreak=¨newline¨/»«/math»
نكتب الآن معادلة الحركة في اتجاه نحو أعلى السطح المائل (في اتجاه المحور x الذي تم تحيده) للجسم 2:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»f«/mi»«mrow»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«/menclose»«/math»
نعبر عن قوة الاحتكاك الساكن في كل من المعادلات المحددة ونعوّض في متباينة الاحتكاك الساكن:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#8804;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mfenced mathcolor=¨#0000FF¨»«mn»1«/mn»«/mfenced»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gsin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#8804;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»gcos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mfenced mathcolor=¨#0000FF¨»«mn»2«/mn»«/mfenced»«/math»
نقوم بجمع المتبانيتين 1 و 2 ونعبر عن فرق الكتلة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8804;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gcos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gcos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8804;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gcos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»/«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»:«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gsin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8804;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8804;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mstyle displaystyle=¨true¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«/mstyle»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8804;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«/math»
حصلنا على الشرط حتى تبقى المجموعة في حالة سكون.
يمكن الآن استنتاج أن الحد الأقصى للفرق بين الكتلتين الذي بحيث تبقى المجموعة في حالة سكون هو:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«/menclose»«/math»
11. جسمان موصولان يسقطان في سقوط حر

11.1. جسمان موصولان يسقطان سقوطًا حرًا
يتحرك الجسمان إلى أسفل معًا.
سنقوم بتعيين اتجاه المحور Y لأسفل.
تؤثر قوتان على الجسم 1: قوة الجاذبية W1 وقوة التوتر T.
نرسم مخططًا للقوى المؤثرة على الجسم 1:
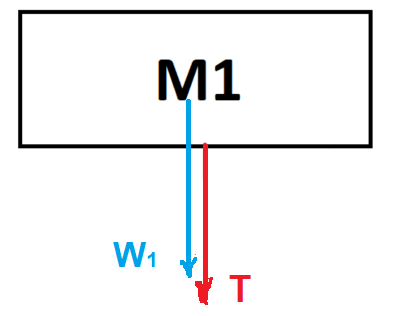
الجسمان موصولان بواسطة خيط مشدود ، لذا فإن تسارعهما متساوٍ. نُشير لتسارعهما المشترك بـ a.
نكتب معادلات الحركة في المحور Y:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mfenced mathcolor=¨#0000FF¨»«mn»1«/mn»«/mfenced»«mspace linebreak=¨newline¨/»«/math»
نرسم مخططًا للقوى المؤثرة على الجسم 2:
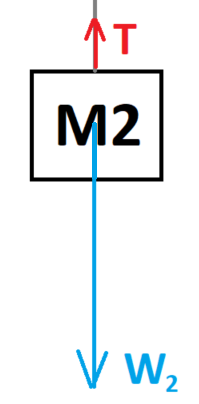
نكتب معادلات الحركة في اتجاه المحور Y:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»y«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#8943;«/mo»«mo mathcolor=¨#0000FF¨»§#160;«/mo»«mfenced mathcolor=¨#0000FF¨»«mn»2«/mn»«/mfenced»«/math»
نجمع المعادلتين المشار لهما:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/math»
نعوّض تعبير التسارع في المعادلة الأولى:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«/menclose»«/math»