حلول التدريبات العملية في الحقل المغناطيسي
62. ו.4.3
من التعبير عن نصف قطر المسار كدالة لفرق الجهد في المصفاة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»d«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«/mstyle»«/math»
يمكن ملاحظة أنه في الرسم البياني الذي يصف نصف قطر المسار كدالة لفرق الجهد، فإن التعبير عن ميل الرسم البياني هو:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»d«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«/mstyle»«/math»
نحسب قيمة ميل الرسم البياني باستخدام نقطتين تقعان على الخط المستقيم:
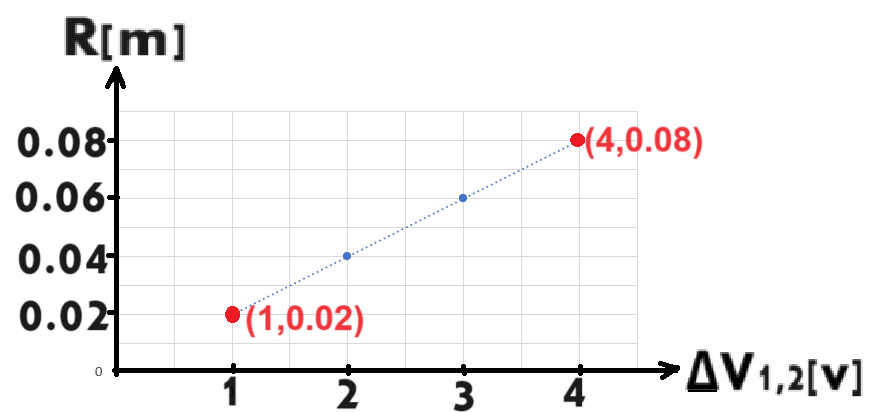
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»08«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»02«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»06«/mn»«/mrow»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»02«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»V«/mi»«/mfrac»«/mstyle»«/math»
نجد كتلة الجسيم من خلال مقارنة تعبير الميل بقيمة الميل:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»d«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»02«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»d«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»02«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»d«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»02«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»90«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»kg«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»gr«/mi»«/mstyle»«/math»
وبالتالي فإن كتلة الجسيم هي 1 غرام.