حلول التدريبات العملية في الدوائر الكهربائية

41. ו.1

أ- يتدفق التيار خارج مصدر فرق الجهد من الجهد العالي إلى الجهد المنخفض، لذا فإن المصدر 1 يُكوّن تيارًا في اتجاه عقارب الساعة. يقوم المصدر 2 أيضًا بتكوين تيار في اتجاه عقارب الساعة.

لذلك، يعمل كل من المصدران تيار في نفس الاتجاه.

ب- نظرًا لأن كلا مصدري فرق الجهد يعمل كل منهما تيارًا في اتجاه عقارب الساعة، فسوف يتدفق تيار في اتجاه عقارب الساعة في الدائرة.

ج- نجد التيار في الدائرة باستخدام قوانين كيرخوف.

يعمل كل من المصدرين تيارًا في اتجاه عقارب الساعة، ويتدفق كل من التيارين في نفس الاتجاه. نشير إلى التيار في الدائرة بواسطة I.

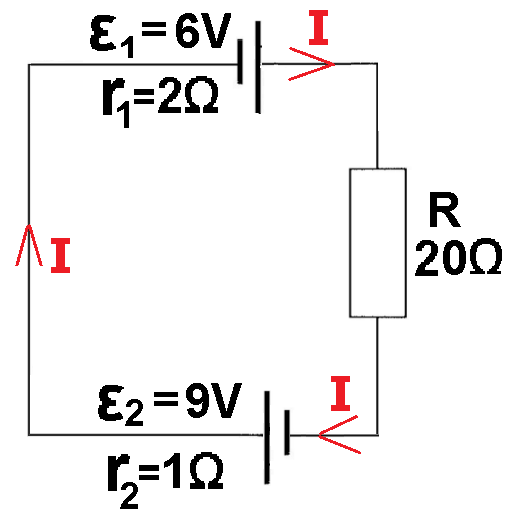
من قانون كيرخوف لفرق الجهد، فإن مجموع فروق الجهد في حلقة مغلقة يساوي صفرًا.

لا يوجد سوى حلقة واحدة في الدائرة، نكتب معادلة فروق الجهد.

قبل كتابة المعادلة، نضيف المقاومات الداخلية إلى الدائرة. وأسهم تمثل فروق الجهد لجميع مكونات الدائرة (نضع رؤوس الأسهم في الجهد العالي).

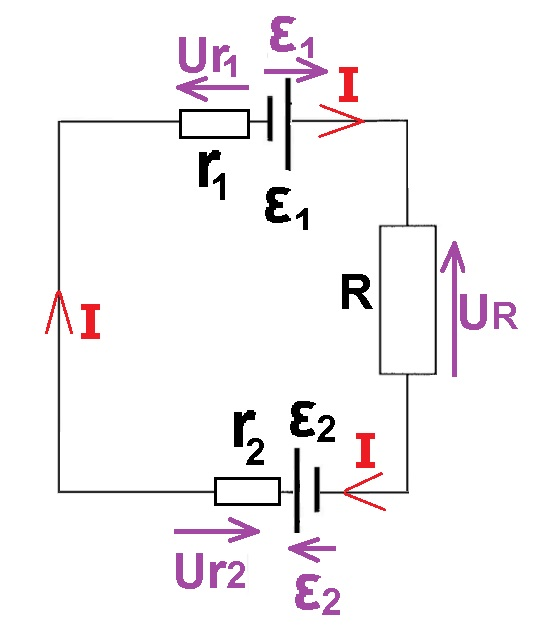
من قانون فروق الجهد لكيرخوف ، فإن مجموع فروق الجهد في كل حلقة مغلقة يساوي صفرًا.

دعنا نجمع فروق الجهد في الحلقة، بدءًا من القطب الموجب للمصدر 1:

نعبر عن معادلات فروق الجهد باستخدام التيار في الدائرة والقوى الكهربائية الدافعة والمقاومة الداخلية:

«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/mstyle»«/math»

نجد من هذه المعادلة التيار في الدائرة:

«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»23«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»15«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨ mathsize=¨24px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨24px¨»15«/mn»«/mrow»«mrow»«mo mathvariant=¨bold¨ mathsize=¨24px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨24px¨»23«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»65«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»A«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»

لذلك ، فإن شدة التيار في الدائرة هو 0.65 أمبير.