حلول التدريبات العملية 1 في الكهروستاتيكا
26.2
حسب تعريف شدة الحقل«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mover»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨»q«/mi»«/mfrac»«/mstyle»«/math» النقطة التي تكون فيها شدة الحقل تساوي صفرًا هي النقطة التي تكون فيها القوة الكهربائية المحصّلة المؤثرة على شحنة الفحص تساوي صفرًا.
النقطة التي تكون فيها محصّلة القوى الكهربائية التي تعمل على شحنة الفحص مساوية للصفر، تقع في المنطقة الواقعة بين اللوح والشحنة النقطية.
فقط في هذا المنطقة تعمل القوى الكهربائية في اتجاهين متعاكسين.
نُشير للبعد بين شحنة الفحص q والشحنة النقطية Q بـ «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mstyle»«/math» .
يتم وصف البعد «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mstyle»«/math» والقوى الكهربائية في الشكل التالي:
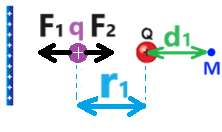
نكتب معادلة الحركة، عندما تكون شحنة الفحص في النقطة التي تكون فيها محصّلة القوى المؤثرة عليها يساوي صفرًا.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»Q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»Q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»q«/mi»«/menclose»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»q«/mi»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»Q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«/menclose»«/mstyle»«/math»
نُعبّر عن «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mstyle»«/math» من معادلة القوى:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»Q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»Q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»§#963;«/mi»«/mfrac»«/msqrt»«/mstyle»«/math»
نُعوّض معطيات السؤال ونحسب البعد «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mstyle»«/math»:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»r«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨ mathsize=¨22px¨»K«/mi»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»Q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»0«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨ mathsize=¨22px¨»§#963;«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»9«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«mn mathvariant=¨bold¨ mathsize=¨22px¨»9«/mn»«/msup»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»5«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«mrow»«mo mathvariant=¨bold¨ mathsize=¨22px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»9«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»8«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨».«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»85«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«mrow»«mo mathvariant=¨bold¨ mathsize=¨22px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»12«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»5«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨».«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»31«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«mrow»«mo mathvariant=¨bold¨ mathsize=¨22px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»11«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»7«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨».«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»965«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«mrow»«mo mathvariant=¨bold¨ mathsize=¨22px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»5«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨».«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»31«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«mrow»«mo mathvariant=¨bold¨ mathsize=¨22px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»11«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathsize=¨22px¨»15«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»87«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»m«/mi»«/math»