ألبوم الحلول في الجاذبية

1. 2023,6 - حركة كواكب سيّارة حول نجم.

______________________________________________________________________________________

• مجلد
• الجواب النهائي
• إستراتيجية
• الحل الكامل
• انتبهوا

...

 

القانون الثالث لكبلر.

ومن القانون الثالث لكبلر، فإن النسبة بين مربع زمن الدورة ومكعب نصف قطر المدار ثابتة.

وقد وجدنا هذه النسبة من الجدول حسب معطيات الكوكب السيّار  b :

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»b«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«msup»«msub»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»b«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«msup»«mn mathvariant=¨bold¨»51«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«msup»«mn mathvariant=¨bold¨»73«/mn»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»44«/mn»«mfrac mathcolor=¨#0000FF¨»«msup»«mi mathvariant=¨bold¨»day«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mrow»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»27«/mn»«/msup»«msup»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«/mfrac»«/mstyle»«/math»

نحسب زمن دورة الكوكب C:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«msup»«msub»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»44«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msup»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»44«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msup»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»44«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»44«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»36«/mn»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»44«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»13«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»14«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»78«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»day«/mi»«/mstyle»«/math»

نحسب نصف القطر المداري للكوكب السيّار d:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»d«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«msup»«msub»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»d«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»44«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msup»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»d«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»d«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»44«/mn»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mfrac»«msup»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»d«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»44«/mn»«/mrow»«/mfrac»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mfrac»«msup»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»05«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»44«/mn»«/mrow»«/mfrac»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»16«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»44«/mn»«/mrow»«/mfrac»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»37«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»27«/mn»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/mstyle»«/math»

نُضيف القيم المحسوبة إلى الجدول:

נמצא יחס זה מהטבלה, בהתאם לנתוני כוכב הלכת b :

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»b«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«msup»«msub»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»b«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«msup»«mn mathvariant=¨bold¨»51«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«msup»«mn mathvariant=¨bold¨»73«/mn»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»44«/mn»«mfrac mathcolor=¨#0000FF¨»«msup»«mi mathvariant=¨bold¨»day«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mrow»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»27«/mn»«/msup»«msup»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«/mfrac»«/mstyle»«/math»

נחשב את זמן המחזור של כוכב C:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«msup»«msub»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»44«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msup»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»44«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msup»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»44«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»44«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»36«/mn»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»44«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»13«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»14«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»78«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»day«/mi»«/mstyle»«/math»

נחשב את רדיוס המסלול של כוכב d:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»d«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«msup»«msub»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»d«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»44«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msup»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»d«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»d«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»44«/mn»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mfrac»«msup»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»d«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»44«/mn»«/mrow»«/mfrac»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mfrac»«msup»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»05«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»44«/mn»«/mrow»«/mfrac»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»16«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»44«/mn»«/mrow»«/mfrac»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»37«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»27«/mn»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/mstyle»«/math»

נוסיף את הערכים המחושבים לטבלה:

1. بشكل عام، نستخدم المقادير الفيزيائية في الوحدات القياسية.

    في هذه الحالة، يجب أن نحسب الوقت الناقص بوحدات غير قياسية (أيام)، لأننا نستخدم معطيات موجودة بوحدات غير قياسية

    يوصى بوصف العلاقة التي تم الحصول عليها من القانون الثالثرلكبلر في الوحدات غير القياسية. 

2. عندما نضع الوحدات القياسية، فإننا نعلم أن النتيجة التي يتم الحصول عليها أيضًا بالوحدات القياسية.

       عند تعويض وحدات غير قياسية والحصول على وحدات غير قياسية، يكون ارتكاب الأخطاء أسهل بكثير.

       يوصى بكتابة تعبير بالوحدات، ومعرفة كيفية ترتيب الوحدات: 

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msqrt mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»44«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»c«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/msqrt»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msqrt mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»44«/mn»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»[«/mo»«mfrac mathcolor=¨#007F00¨»«msup»«mi mathvariant=¨bold¨»day«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mrow»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»27«/mn»«/msup»«msup»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ stretchy=¨true¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»36«/mn»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»[«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#007F00¨»10«/mn»«mrow mathcolor=¨#007F00¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#007F00¨»m«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/msqrt»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msqrt mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»44«/mn»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»[«/mo»«mfrac mathcolor=¨#007F00¨»«msup»«mi mathvariant=¨bold¨»day«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mrow»«menclose notation=¨updiagonalstrike¨»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»27«/mn»«/msup»«/menclose»«menclose notation=¨downdiagonalstrike¨»«msup»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/menclose»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ stretchy=¨true¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«msup»«mn mathvariant=¨bold¨»36«/mn»«mn mathvariant=¨bold¨»3«/mn»«/msup»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»[«/mo»«menclose mathcolor=¨#007F00¨ notation=¨updiagonalstrike¨»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»27«/mn»«/mrow»«/msup»«/menclose»«menclose mathcolor=¨#007F00¨ notation=¨downdiagonalstrike¨»«msup»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/menclose»«mo mathvariant=¨bold¨ stretchy=¨true¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msqrt mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»44«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«msup»«mn mathvariant=¨bold¨»36«/mn»«mn mathvariant=¨bold¨»3«/mn»«/msup»«mrow»«mo stretchy=¨true¨ mathvariant=¨bold¨»[«/mo»«msup»«mi mathcolor=¨#007F00¨ mathvariant=¨bold¨»day«/mi»«mn mathcolor=¨#007F00¨ mathvariant=¨bold¨»2«/mn»«/msup»«mo stretchy=¨true¨ mathvariant=¨bold¨»]«/mo»«/mrow»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msqrt mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»78«/mn»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»[«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#007F00¨»day«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#007F00¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ stretchy=¨true¨»]«/mo»«/mrow»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»4«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»day«/mi»«/mstyle»«/math»

    במקרה זה, יש לחשב את הזמן החסר ביחידות לא תקניות (ימים) , מכיוון שאנחנו משתמשים בנתונים שהם ביחידות לא תקניות

    מומלץ לתאר את היחס המתקבל מחוק שלישי של קפלר ביחידות לא תקניות.

2. כשאנחנו מציבים ביחידות תקניות אנחנו יודעים שגם התוצאה תתקבל ביחידות תקניות. 

      כאשר מציבים ביחידות לא תקניות ומקבלים יחידות לא תקניות, הרבה יותר קל לטעות.

      מומלץ לכתוב ביטוי עם היחידות , ולראות כיצד היחידות מסתדרות:

______________________________________________________________________________________

______________________________________________________________________________________

• مجلد
• الجواب النهائي
• إستراتيجية
• الحل الكامل
• انتبهوا

...

أيمن ليس على حق.

التعبير عن سرعة الكوكب السيّار بدلالة نصف القطر من معادلة الحركة الدائرية. 

كلما كان الكوكب السيّار أبعد، كلما زاد نصف قطر مداره.

على الكوكب السيّار، تعمل الجاذبية العامة فقط كقوة جاذبة مركزية، نرسم مخططًا للقوى: 

لنكتب معادلة الحركة الدائرية:

نُشير إلى كتلة الكوكب بـ m وكتلة الكوكب القزم بـ M.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«menclose notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/msqrt»«/menclose»«/math»

ومن خلال التعبير يمكن ملاحظة أنه كلما زاد نصف قطر مدار الكوكب، قلت سرعة الكوكب، وبالتالي فإن أيمن ليس على حق.

כדי לקבוע אם איתן צודק או לא , נכתוב את משוואת התנועה המעגלית של כוכב לכת ונבטא ממנה את המהירות בתלות ברדיוס הסיבוב.

נסמן את מסת כוכב הלכת ב- m ואת מסת הכוכב הננסי ב- M.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«menclose notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/msqrt»«/menclose»«/math»

מהביטוי ניתן לראות שככל שרדיוס מסלול תנועת הכוכב גדול יותר, כך מהירות הכוכב קטנה יותר, לכן איתן לא צודק.

1. للإجابة على الأسئلة الفيزيائية يجب عليك استخدام المبادئ الفيزيائية، الأسئلة في الفيزياء ليست أسئلة منطقية أو ألغاز. 

2. لفحص اعتماد مقدار فيزيائي معين على مقدار فيزيائي آخر، يجب تطوير تعبير مناسب، وعادة ما يتم تطوير التعبير من معادلات الحركة. 

     

2. כדי לבדוק תלות של גודל פיזיקלי מסוים מגודל פיזיקלי אחר, יש לפתח ביטוי מתאים, לרוב הביטוי מפתוח ממשוואות התנועה.

______________________________________________________________________________________

______________________________________________________________________________________

• مجلد
• الجواب النهائي
• إستراتيجية
• الحل الكامل
• انتبهوا

...

 «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»g«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»b«/mi»«/msub»«mo mathvariant=¨bold¨ mathsize=¨20px¨»=«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨ mathsize=¨20px¨»4«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#960;«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨20px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#160;«/mo»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»r«/mi»«/mrow»«mi mathvariant=¨bold¨ mathsize=¨20px¨»T«/mi»«/mfrac»«/math»

تعبير التسارع من معادلة الحركة الدائرية.

يجب التعبير عن تسارع الكوكب السّيار b في حركته حول الكوكب القزم. 

نكتب معادلة الحركة باستخدام تسارع الكوكب السّيار:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»b«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«/msup»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»g«/mi»«mi mathvariant=¨bold¨»b«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«/menclose»«/mstyle»«/math»

נכתוב את משוואת התנועה בעזרת תאוצת הכוכב:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨»«mo stretchy=¨true¨»(«/mo»«mfrac»«mrow»«mn»2«/mn»«mo»§#183;«/mo»«mi»§#960;«/mi»«/mrow»«mi»T«/mi»«/mfrac»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»b«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«/msup»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»g«/mi»«mi mathvariant=¨bold¨»b«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«/menclose»«/mstyle»«/math»

 

1. على الرغم من أن التسارع يُشار إليه بـ -  g_b، إلا أنه يجب التعبير عن تسارع الكوكب السيّار b حول الكوكب القزم، وليس التسارع على سطح الكوكب السيّار b. 

2. يتحرك الكوكب في حركة دائرية منتظمة، والتسارع المطلوب هو التسارع المركزي (راديالي) لحركة الكوكب السيّار. 

     نستخدم تعبير التسارع الراديالي لتطوير التعبير المطلوب:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»R«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/menclose»«/mstyle»«/math»

3. يظهر تعبير التسارع الراديالي في صفحات القوانين:

 

2. כוכב הלכת נע בתנועה מעגלית קצובה, התאוצה המבוקשת היא התאוצה הרדיאלית של תנועת הכוכב.

     נשתמש בביטוי התאוצה הרדילית כדי לפתח את הביטוי הדרוש:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»R«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/menclose»«/mstyle»«/math»

3. ביטוי התאוצה הרדיאלית מופיע בדפי הנוסחאות:

 

______________________________________________________________________________________

______________________________________________________________________________________

• مجلد
• الجواب النهائي
• إستراتيجية
• الحل الكامل
• انتبهوا

______________________________________________________________________________________

______________________________________________________________________________________

• مجلد
• الجواب النهائي
• إستراتيجية
• الحل الكامل
• انتبهوا

______________________________________________________________________________________

______________________________________________________________________________________

• مجلد
• الجواب النهائي
• إستراتيجية
• الحل الكامل
• انتبهوا

...

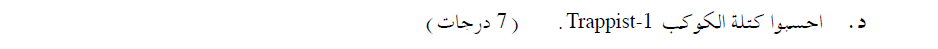
 «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»E«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»E«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»11«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»05«/mn»«/mstyle»«/math»

إضافة الطاقة اللازمة للسفينة الفضائية للهروب من مجال الجاذبية تساوي القيمة المطلقة للطاقة الكلية المركبة الفضائية. 

كل جسم يتحرك في حركة قمر اصطناعي حول نجم لديه طاقة سالبة، لكي يفلت الجسم من تأثير الجاذبية يجب أن يعطى طاقة إضافية بحيث تكون طاقته صفر، وبالتالي فإن الطاقة الإضافية اللازمة تساوي القيمة المطلقة لـ الطاقة الكلية للقمر الاصطناعي.

نُعبر عن النسبة اللازمة باستخدام نسبة القيمة المطلقة للطاقاة المطلقة:

كلتا السفينتين الفضائيتين لهما نفس الكتلة، نشير إلى كتلتهما بالرمز m.

كلتا السفينتين الفضائيتين لهما نفس نصف قطر المدار، نشير إلى نصف قطر مسار الدوران بالرمز r. 

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»E«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»E«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle displaystyle=¨true¨»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»|«/mo»«mfrac»«mrow»«menclose notation=¨updiagonalstrike¨»«mo»-«/mo»«mi»G«/mi»«/menclose»«mo»§#183;«/mo»«msub»«mi»M«/mi»«mi»s«/mi»«/msub»«mo»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi»m«/mi»«/menclose»«/mrow»«mrow»«menclose notation=¨updiagonalstrike¨»«mn»2«/mn»«/menclose»«mo»§#183;«/mo»«menclose notation=¨horizontalstrike¨»«mi»r«/mi»«/menclose»«/mrow»«/mfrac»«mo stretchy=¨true¨»|«/mo»«/mstyle»«/mstyle»«mstyle displaystyle=¨true¨»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»|«/mo»«mfrac»«mrow»«menclose notation=¨updiagonalstrike¨»«mo»-«/mo»«mi»G«/mi»«/menclose»«mo»§#183;«/mo»«msub»«mi»M«/mi»«mi»Tr«/mi»«/msub»«mo»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi»m«/mi»«/menclose»«/mrow»«mrow»«menclose notation=¨updiagonalstrike¨»«mn»2«/mn»«/menclose»«mo»§#183;«/mo»«menclose notation=¨horizontalstrike¨»«mi»r«/mi»«/menclose»«/mrow»«/mfrac»«mo stretchy=¨true¨»|«/mo»«/mstyle»«/mstyle»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»Tr«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»99«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»30«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»29«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»11«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»05«/mn»«/math»

נבטא את היחס הדרוש בעזרת יחס הערך המוחלט של האנרגיות הכוללות:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»E«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»E«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle displaystyle=¨true¨»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»|«/mo»«mfrac»«mrow»«menclose notation=¨updiagonalstrike¨»«mo»-«/mo»«mi»G«/mi»«/menclose»«mo»§#183;«/mo»«msub»«mi»M«/mi»«mi»s«/mi»«/msub»«mo»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi»m«/mi»«/menclose»«/mrow»«mrow»«menclose notation=¨updiagonalstrike¨»«mn»2«/mn»«/menclose»«mo»§#183;«/mo»«menclose notation=¨horizontalstrike¨»«mi»r«/mi»«/menclose»«/mrow»«/mfrac»«mo stretchy=¨true¨»|«/mo»«/mstyle»«/mstyle»«mstyle displaystyle=¨true¨»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»|«/mo»«mfrac»«mrow»«menclose notation=¨updiagonalstrike¨»«mo»-«/mo»«mi»G«/mi»«/menclose»«mo»§#183;«/mo»«msub»«mi»M«/mi»«mi»Tr«/mi»«/msub»«mo»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi»m«/mi»«/menclose»«/mrow»«mrow»«menclose notation=¨updiagonalstrike¨»«mn»2«/mn»«/menclose»«mo»§#183;«/mo»«menclose notation=¨horizontalstrike¨»«mi»r«/mi»«/menclose»«/mrow»«/mfrac»«mo stretchy=¨true¨»|«/mo»«/mstyle»«/mstyle»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»Tr«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»99«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»30«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»29«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»11«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»05«/mn»«/math»

 

1. يظهر التعبير عن الطاقة الكلية لجسم يتحرك في حركة القمر الاصطناعي على صفحات القوانين: 

2. الطاقة الكلية لجسم يتحرك في حركة قمر اصطناعي تساوي مجموع طاقة الوضع الجاذبية والطاقة الحركية. 

     

3. الاستنتاج من تعبير النسبة لإضافة الطاقة اللازمة هو أنه كلما زادت كتلة النجم (الذي تتم حوله الحركة الدائرية)، 

   فإن الطاقة الإضافية اللازمة لهروب القمر الاصطناعي تكون أكبر. 

2. האנרגיה הכוללת של גוף הנע בתנועה לוויינית שווה לסכום האנרגיה הפוטנצילאית כובדית והאנרגיה הקינטית.

     

3. המסקנה מביטוי היחס הדרוש היא שככל שמסת הכוכב (סביבו מתקיימת התנועה המעגלית) גדול יותר , 

    כך תוספת האנרגיה הדרושה להימלטות הלוויין היא גדולה יותר.

______________________________________________________________________________________