ألبوم الحلول في الجاذبية

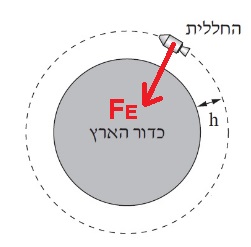
3. 2019,6- سفينة فضائية تدور حول الكرة الأرضية وتهبط إلى سطح الأرض

______________________________________________________________________________________

...

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»7780«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»

رسم مخطّط القوى المؤثرة وكتابة معادلات الحركة.

فقط قوة الجاذبية التي تشغّلها الأرض تؤثر على سفينة الفضاء.

نرسم مخطّط القوى التي تؤثر على السفينة الفضائية:

نكتب معادلات الحركة ، ونعبر عن سرعة القمر الصناعي منها:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«mstyle mathvariant=¨bold¨»«mrow»«mo»(«/mo»«msub»«mi»R«/mi»«mi»E«/mi»«/msub»«mo»+«/mo»«mi»h«/mi»«mo»)«/mo»«/mrow»«/mstyle»«menclose notation=¨downdiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«menclose notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»h«/mi»«/menclose»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»h«/mi»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»11«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»974«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»24«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»38«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»190«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»98«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»14«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»57«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»60«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»57«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»78«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msup»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»

ومن هنا سرعة المركبة الفضائية 7780 مترا في الثانية.

נערוך תרשים כוחות:

נכתוב את משוואות התנועה, ונבטא ממנה את מהירות הלוויין:

מכאן שמהירות החללית היא 7,780 מטר לשנייה.

1. يجب استخدام نصف قطر الأرض وليس نصف قطر مسار الكرة الأرضية.

2. مكتوب في السؤال "استخدم الثوابت المعطاة في صفحة الصيغة"، يجب أن تجد مقدار السرعة ولا تجد تعبيرًا عن السرعة.

سيكون من الأصح أن تكتب استخدم قيم الثوابت.

2. בשאלה כתוב "השתמש בקבועים הנתונים בדף הנוסחאות", יש למצוא את גודל המהירות ולא למצוא ביטוי למהירות.

היה נכון יותר לכתוב השתמש בערכי הקבועים.

______________________________________________________________________________________

...

الطالبة مخطئة، المركبة الفضائية لا تتحرك في خط مستقيم.

فهم القانون الأول لنيوتن

يكون الجسم متزنًا فقط إذا كانت سرعة الجسم لا تتغير في المقدار والاتجاه. لذلك الطالبة ليست على حق.

من الممكن تحديد ما إذا كان الجسم ثابتًا بمساعدة الكينماتيكا أو بمساعدة الديناميكا.

من حيث الكينماتيكا - يكون الجسم ثابتًا فقط إذا كانت سرعته لا تتغير في المقدار ولا تتغير في الاتجاه.

من حيث الديناميكا - وفقًا لقانون نيوتن الأول، يكون الجسم ثابتًا عندما تكون محصّلة القوى مساويًا للصفر

______________________________________________________________________________________

...

مقدار السرعة لا يتغير ، من تعبير السرعة يمكنك أن ترى أن السرعة لا تتعلق بكتلة السفينة الفضائية.

استخدام تعبير السرعة.

من تعبير عن سرعة السفينة الفضائية في القسم أ: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»h«/mi»«/mrow»«/mfrac»«/msqrt»«/math» السرعة لا تتعلق على كتلة السفينة الفضائية.

לכן, אם מסת החללית הייתה גדולה יותר גודל מהירות החללית לא הייתה משתנה.

بشكل عام، يجب أن يشمل الحل الكامل على تعبير للإجابة النهائية. تعتبر الإجابة بدون تعبير عام إجابة غير كاملة حتى لو كانت صحيحة.

بالإضافة إلى أهمية كتابة الحل الصحيح، فإن كتابة العبارة للإجابة في أحد الأقسام تجعل من الممكن الإجابة على قسم آخر، كما يتضح من هذا السؤال.

מעבר לחשיבות כתיבת פתרון תקין , כתיבת הביטוי לתשובה בסעיף אחד מאפשרת לענות על סעיף אחר, כפי שניתן לראות בשאלה זו.

______________________________________________________________________________________

جـ.

______________________________________________________________________________________

...

الطاقة الميكانيكية الكلية سوف تقل، من تعبير الطاقة لجسم يتحرك في حركة قمر اصطناعي.

التعبير للطاقة الميكانيكية للقمر الاصطناعي.

من تعبير الطاقة الميكانيكية الكلية لجسم يتحرك في حركة قمر اصطناعي: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«/math» كلما زادت كتلة المركبة الفضائية،كلما اصبحت الطاقة الميكانيكية الكلية أكثر سالبة، أي كلما قلت.

1. تعبير الطاقة الميكانيكية للقمر الاصطناعي موجودة في صفحات الصيغة، ولا داعي لتطوير التعبير:

1. إن تعبيرات الطاقة مناسبة للحركة الدائرية فقط وليست للحركة في خط مستقيم. حتى عندما يتحرك الجسم في خط مستقيم تحت تأثير الجاذبية وحدها.

3. التعبير عن الطاقة الوضعية مناسب للحركة الدائرية وكذلك للحركة في خط مستقيم.

4. الطاقة الميكانيكية الكلية سالبة عندما نتحدث عن هيئة مترابطة، فكلما زادت كتلة السفينة الفضائية، زادت قوة الجاذبية. تكون الهيئة أكثر ارتباطًا، الطاقة الكلية تكون أكثر سالبة، أي تأخذ بالنقصان.

5. حسب الملاحظة "انتبه إلى إشارة الطاقة"، يمكن فهم أن الإشارة ليست إلى القيمة المطلقة للطاقة.

2. ביטויי האנרגיה מתאימים לתנועה מעגלית בלבד ולא לתנועה בקו ישר. גם כאשר הגוף נע בקו ישר בהשפעת כוח הכבידה בלבד.

3. ביטוי האנרגיה הפוטנצאילית מתאים לתנועה מעגלית וגם לתנועה בקו ישר.

4. אנרגיה כוללת שלילית כאשר מדובר במערכת קשורה , ככל שמסת החללית גדולה יותר כוח הכבידה יותר גדול.

המערכת יותר קשורה, האנרגיה הכוללת יותר שלילית, יותר קטנה.

5.מההערה "שים לב לסימן של האנרגיה" , ניתן להבין שהכוונה היא לא לערך המוחלט של האנרגיה.

______________________________________________________________________________________

...

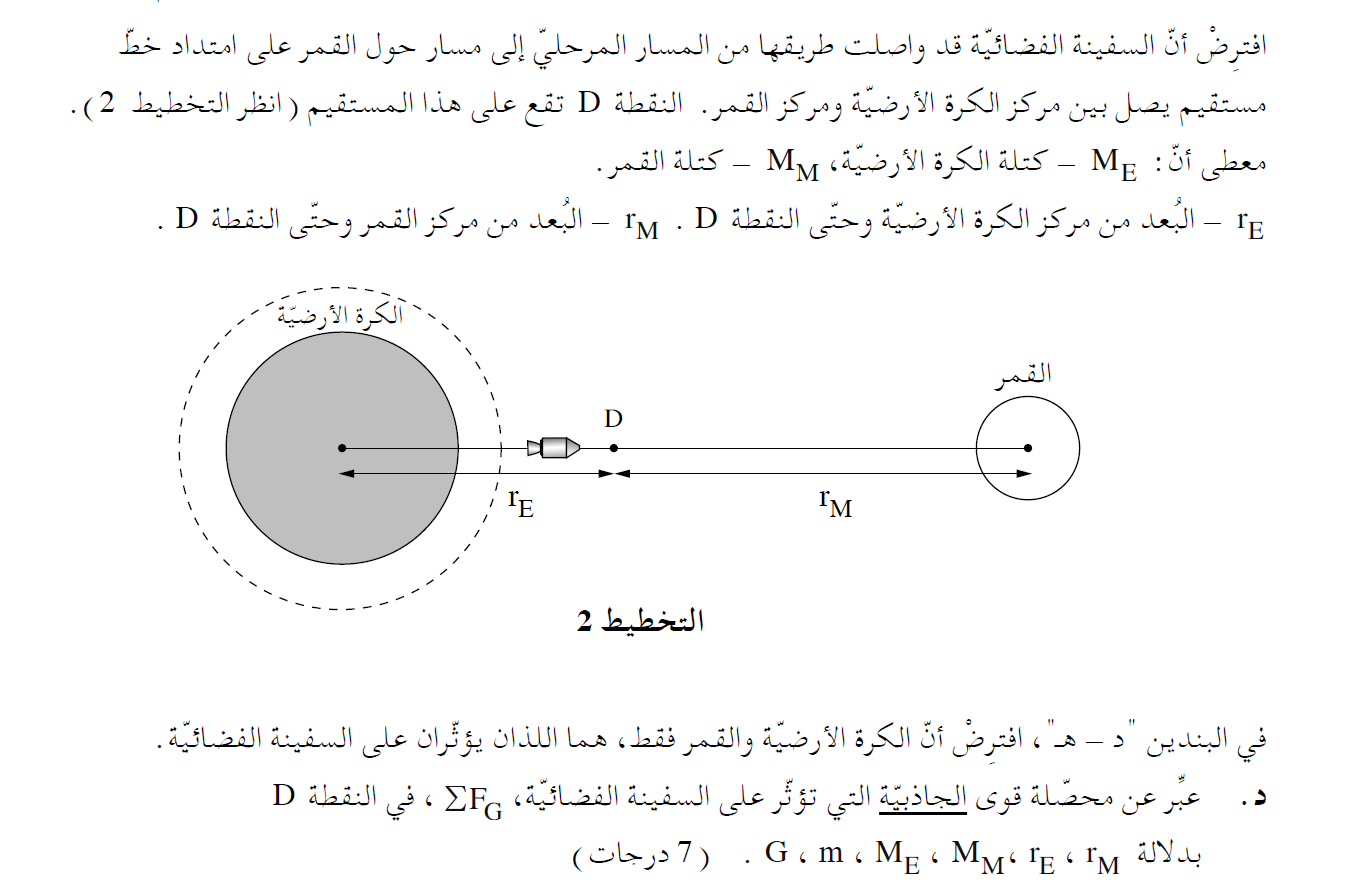
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨»§#931;F«/mi»«mi mathvariant=¨bold¨»G«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»M«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»M«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«/math»

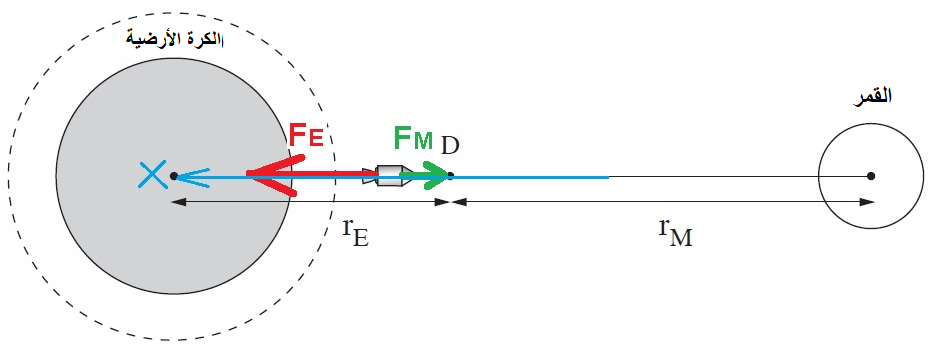
قانون الجاذبية العام

تؤثر قوتان جاذبيتان على سفينة الفضاء، نرسم مخطط للقوى:
نشير إلى قوة الجاذبية التي يُشغّلها القمر بـ F_M ، وقوة الجاذبية التي تشغّلها الأرض بـ F_E.

سنكتب تعبيرًا عن القوة المحصّلة نسبة لمحور موجّه إلى اليسار ، نحو الكرة الأرض.

نستخدم قانون الجاذبية العام:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»G«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»G«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»M«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»M«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«/math»

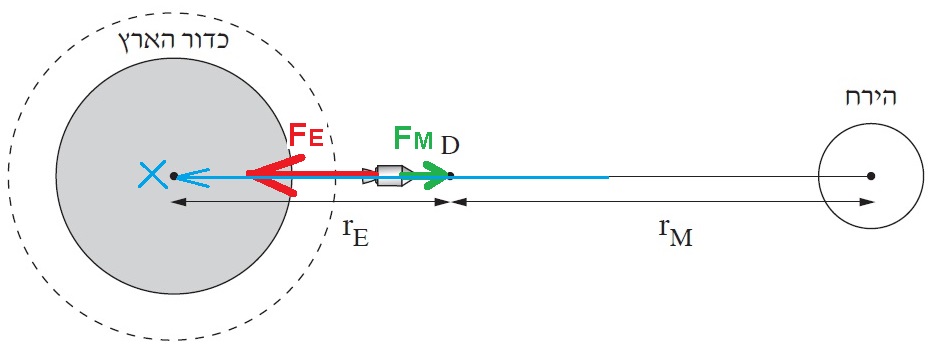
נסמן את כוח הכבידה שמפעיל הירח ב FM , ואת כוח הכבידה שמפעיל כדור הארץ ב FE.

נכתוב ביטוי לכוח השקול ביחס לציר שכיוונו שמאלה, לכיוון כדור הארץ.

נשתמש בחוק הכבידה האוניברסלי:

يجب وصف كل واحدة من القوى نسبة لمحور الحركة الذي تم اختياره. تعبير القوة المحصّلة متعلق بهذا المحور.

בפתרון המוצע כאן כיוון הציר הנבחר הוא שמאלה לכן כוח הכבידה שמפעיל כדור הארץ הוא חיובי, וכוח הכבידה שמפעיל הירח הוא שלילי.

בהתאם, כאשר ערך הכוח השקול הוא חיובי כיוון הכוח השקול הוא שמאלה, וכאשר הכוח שלילי כיוון הכוח השקול ימינה.

תשובה מלאה לסעיף זה היא רק תשובה הכוללת ציר מקום נבחר.

______________________________________________________________________________________

الرسم البياني الملائم هو الرسم البياني 2.

تحديد الرسم البياني المناسب باستخدام تعبير القوة المحصّلة لوصف عام للقوة وقيم خاصة.

نعبّر عن القوة المحصّلة المؤثرة على السفينة الفضائية كدالة لمسافة السفينة الفضائية من مركز الأرض r.

نشير للبعد بين مركز الكرة الأرضية ونقطة مركز الفمر بـ «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»EM«/mi»«/msub»«/math».

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»G«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»M«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»M«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»G«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»M«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«mstyle mathvariant=¨bold¨»«mrow»«mo»(«/mo»«msub»«mi»d«/mi»«mi»EM«/mi»«/msub»«mo»-«/mo»«mi»r«/mi»«mo»)«/mo»«/mrow»«/mstyle»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»

من تعبير محصلة القوى يمكن ملاحظة أن قوة الجاذبية المحصلّة ليست ثابتة ولا خطية كدالة لـ r. لذلك ، لا يتوافق الرسمان البيانيان 1 و 3 مع وصف محصلة القوى.

كتلة الأرض أكبر من كتلة القمر، وبالتالي فإنمحصلة القوى يساوي صفرًا بالقرب من القمر، وبالتالي فإن الرسم البياني المناسب هو الرسم البياني 2.

נסמן את המרחק בין נקודת מרכז כדור הארץ לנקודת מרכז הירח ב «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»EM«/mi»«/msub»«/math».

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»G«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»M«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»M«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»G«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»M«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«mstyle mathvariant=¨bold¨»«mrow»«mo»(«/mo»«msub»«mi»d«/mi»«mi»EM«/mi»«/msub»«mo»-«/mo»«mi»r«/mi»«mo»)«/mo»«/mrow»«/mstyle»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»

מביטוי הכוח השקול ניתן לראות שכוח הכבידה השקול הוא לא קבוע ולא ליניארי בתלות ב r. לכן גרפים 1 ו 3 לא מתאימים לתיאור הכוח השקול.

מסת כדור הארץ גדולה ממסת הירח, מכאן ששקול הכוחות שווה לאפס בסמוך לירח , לכן הגרף המתאים הוא גרף 2.

1. في القسم السابق، يجب التعبير عن القوة المحصّلة كدالة للبعد من القمر والأرض.

في هذا القسم، تتعامل الرسوم البيانية مع البعد من الأرض، لذلك يجب كتابة تعبير جديد.

2. لا داعي لكتابة تفسير، لكن الإجابة الخاطئة بدون تفسير لا تكسب نقاط.

تفسير صحيح يمكن أن تكسب بعض النقاط، لذلك يجب أن تكتب تعليلاً.

בסעיף זה הגרפים עוסקים במרחק מכדור הארץ, לכן יש לכתוב ביטוי חדש.

2. אין צורך לכתוב נימוק אך תשובה לא נכונה ללא נימוק לא מזכה בניקוד .

נימוק נכון יכול לזכות בחלק מהנקודות לכן כדאי לכתוב נימוק.

______________________________________________________________________________________