22. 1994,5- السقوط الحر واعتبارات الطاقة

______________________________________________________________________________________
...
تسارع الجاذبية في النقطة A هو 2.5 مترًا لكل ثانية مربعة، وموجهًا نحو مركز الكرة الأرضية.
كتابة معادلة حركة للجسم عندما يكون في النقطة A ، ومعادلة أخرى للحركة عندما يكون الجسم على سطح الكوكب.
تم الحصول على معادلتين بمجهولين M وتسارع الجاذبية في النقطة A.
الاحتمال الآخر هو كتابة معادلة الحركة بدلالة قوة الجاذبية التي تتعلق ببعد الجسم من نقطة مركز الكوكب. ونعبّر من هذا التعبير عن تسارع الجاذبية بدلالة البعد من مركز الكوكب. ونستنتج من التعبير تسارع الجاذبية في النقطة A.
מתקבלות שתי משוואות עם שני נעלמים M ו- תאוצת הכובד בנקודה A.
אפשרות נוספת לכתוב את משוואת התנועה עם כוח כובד התלוי במרחק הגוף מנקודת מרכז הכוכב . ולבטא מביטוי זה את תאוצת הכובד בתלות במרחק מהכוכב. ולהסיק מסקנה מהביטוי על תאוצת הכובד בנקודה A.
نرسم مخطّط القوى على الجسم الذي يتم تحريره من النقطة A.
نكتب معادلة حركة الجسم عندما يكون في النقطة A، ونعبّر منها عن تسارع السقوط الحر في النقطة A.
نّشير إلى نصف قطر مدار القمر الاصناعي بواسطة RA ، وكتلة الكوكب بمقدار M ونصف قطر الكوكب بواسطة R:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«msub mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«msup»«mfenced»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»h«/mi»«/mrow»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«msup»«mfenced»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«msup»«mfenced»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»g«/mi»«msub»«mo mathvariant=¨bold¨»*«/mo»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
مُعطى نصف قطر الكوكب ولكن كتلة الكوكب عير معلومة. مُعطى تسارع الجاذبية على سطح الكوكب، وهناك علاقة بين تسارع الجاذبية على سطح الكوكب وكتلته.
نكتب معادلة حركة الجسم عندما يكون على سطح الكوكب، ونعبّر عن كتلة الجسم من معادلة الحركة.
نُشير إلى تسارع الجاذبية على سطح الكوكب بـ *g:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»*«/mo»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»G«/mi»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
نعوّض تعبير كتلة الكوكب في تعبير تسارع الجاذبية في النقطة A:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«msub mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»M«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»*«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨downdiagonalstrike¨»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«/menclose»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»*«/mo»«/mrow»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
لذلك فإن تسارع الجاذبية في النقطة A مساوٍ 2.5 مترًا لكل ثانية مربعة وموجهًا نحو مركز الكوكب.
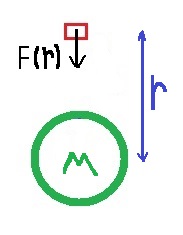
طريقة أخرى: تؤثرعلى الجسم قوة متغيرة من حيث المقدار، والتي تتعلّق ببعد الجسم من مركز الكرة الأرضية، نشير إلى هذا البعد بواسطة r:
نرسم مخطّط للقوى المؤثرة:
نكتب معادلة الحركة اعتمادًا على القوة المتغيرة F ، ونعبّر منها عن التسارع بدلالة r:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»*«/mo»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»r«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/menclose»«/math»
تسارع الجاذبية على سطح الكوكب هو 10 أمتار لكل ثانية مربعة، وفي النقطة A تكون قيمة r أكبر بمرتين من التعبير «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math» تسارع الجاذبية في النقطة A أصغر بأربع مرات.
مقداره 2.5 متر في الثانية واتجاهه نحو مركز الكرة الأرضية.
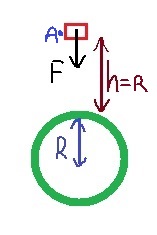
נכתוב את משוואת התנועה לגוף כאשר הוא נמצא בנקודה A , ונבטא ממנה את תאוצת הנפילה החופשית בנקודה A.
נסמן את רדיוס מסלול תנועת הלוויין ב RA ,את מסת הכוכב ב M ואת רדיוס הכוכב ב R :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«msub mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«msup»«mfenced»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»h«/mi»«/mrow»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«msup»«mfenced»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«msup»«mfenced»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»g«/mi»«msub»«mo mathvariant=¨bold¨»*«/mo»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
רדיוס הכוכב נתון אך מסת הכוכב לא נתונה . נתונה תאוצת הכובד על פני הכוכב, ויש קשר בין תאוצת הכובד על פני הכוכב למסת הכוכב.
נכתוב את משוואת התנועה לגוף כאשר הוא נמצא על פני הכוכב , ונבטא ממשוואת התנועה את מסת הגוף .
נסמן את תאוצת הכובד על פני הכוכב ב *g:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»*«/mo»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»G«/mi»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
נציב את ביטוי מסת הכוכב ממשוואת התנועה על פני הכוכב ,במסת הכוכב בביטוי תאוצת הכובד בנקודה A:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«msub mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»M«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»*«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨downdiagonalstrike¨»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«/menclose»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»*«/mo»«/mrow»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
לכן תאוצת הכובד בנקודה A גודלה 2.5 מטר לשנייה בריבוע וכיוונה כלפי מרכז הכוכב.
تتم كتابة معادلة الحركة وفقًا للقوى المؤثرة على الجسم،
إذا تغيرت إحدى القوى، يمكنك كتابة معادلة الحركة مع تسارع متغير، أو كتابة
معادلتين للحركة في حالتين مختلفتين.
الجبر له أشكال مختلفة، وفي النهاية كل الطرق الصحيحة
تؤدي إلى نفس النتيجة.
לאלגברה יש צורות שונות, בסוף כל הדרכים הנכונות מובילות לאותה המסקנה.
______________________________________________________________________________________
أ.

______________________________________________________________________________________
...
وصف الرسم البياني التقريبي وفقًا لدالة معينة.
نكتب أولاً التعبير الرياضي الذي يصف تسارع الجسم كدالة لبُعده عن مركز الكوكب r ، نستخدم التعبير الذي طوّرناه في القسم السابق:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»*«/mo»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»r«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/menclose»«/math»
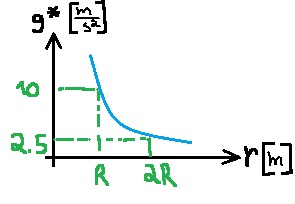
كلما كانت r أكبر، كلما كان التسارع أصغر، وعندما تقترب r إلى اللانهاية ، فإن تسارع الجاذبية يقترب إلى الصفر. وعندما يقترب r إلى الصفر ، فإن تسارع الجاذبية يقترب إلى اللانهاية.
عندما تزيد r مرتين ، يكون تسارع الجاذبية أصغر بأربع مرات ، وبالتالي فإن تسارع الجاذبية لا يقل بصورة خطية كدالة لـ r.
نرسم الرسم البياني بشكل تقريبي، ونشير في الرسم البياني إلى قيمتي النقطتين اللتين تناولهما السؤال:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»*«/mo»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»r«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/menclose»«/math»
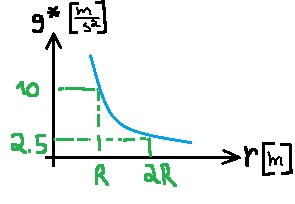
ככל ש r גדול יותר התאוצה קטנה יותר , כאשר r שואף לאין סוף תאוצת הכובד שואפת לאפס. וכאשר r שואף לאפס תאוצת הכובד שואפת לאין סוף.
כאשר r גדל פי 2 , תאוצת הכובד קטנה פי 4 , לכן תאוצת הכובד לא קטנה בצורה ליניארית בתלות ב r .
נסרטט את הגרף ,בצורה מקורבת , נציין בגרף את שתי ערכי הנקודות בהן עסקה השאלה:
1. لا يمكن
الإجابة على هذا السؤال بدقة، من المهم وصف دالة تنازلية بطريقة غير خطية. وفقًا
لتعبير التسارع بدلالة r.
يمكنك تحديد
القيمتين الذي تناولهم السؤال، لكن لا داعي لذلك.
2. من السؤال،
يبدو أنه يتم وصف الرسم البياني أولاً ثم كتابة الدالة، من المهم القيام بالعكس،
ووصف الدالة أولاً ثم وصف الرسم البياني بعد ذلك.
يتم وصف
الرسم البياني وفقًا للدالة.
أحيانًا لا تساعد صياغة السؤال الطالب في الوصول إلى الإجابة الصحيحة، عليك
دائمًا التفكير، وألا تكون ساذجًا. (هذا جيد أيضًا مدى الحياة).
אפשר לציין את שני הערכים בהם עסקה השאלה, אך לא חייבים.
______________________________________________________________________________________
أ. 
______________________________________________________________________________________
...
زمن السقوط أصغر من 2828.42 ثانية ، وأكبر من 1414.21 ثانية.
يجب تحديد مدّة الحركة لكل حالة من الحالتين في حالة الحد الأقصى للتسارع والحد السفلي، افترض أن الجسم يتحرك بتسارع ثابت.
يتحرك الجسم لمسافة 10 ملايين متر بتسارع جاذبية متغير. في نقطة بداية الحركة في النقطة A ، يكون تسارعه 2.5 مترًا لكل ثانية مربعة. وتسارع الجسم على سطح الكوكب هو 10 أمتار لكل ثانية مربعة.
نأخذ الحد الأعلى لمدّة الحركة في حالة أدنى حد ثابت لتسارع الجاذبية ، والحد الأدنى لمدّة الحركة في حالة أقصى تسارع ثابت للجاذبية.
سوف نعبّر عن زمن الحركة من دالة المكان كدالة للزمن المناسبة للحركة بتسارع ثابت، ونشير إلى المحور الذي يكون أصله في نقطة بداية الحركة واتجاهه للأسفل:
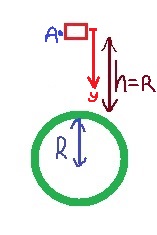
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»Y«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»*«/mo»«/mrow»«/mfrac»«/msqrt»«/mstyle»«/math»
نجد الحد الأدنى والحد الأقصى لمدّة الحركة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mi mathvariant=¨bold¨»min«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»Y«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»g«/mi»«msub»«mo mathvariant=¨bold¨»*«/mo»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»7«/mn»«/msup»«/mrow»«mn mathvariant=¨bold¨»10«/mn»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»414«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»21«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»Y«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»g«/mi»«msub»«mo mathvariant=¨bold¨»*«/mo»«mi mathvariant=¨bold¨»min«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»7«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»828«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»42«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«/mstyle»«/math»
زمن حركة الجسم أكبر من 1414.21 ثانية ، وأقل من 2828.42 ثانية.
נתייחס לגבול עליון כאל זמן תנועה מקסימאלי בתאוצת כובד מינמאלית קבועה , וגבול תחתון זמן תנועה מנימאלי בתאוצת כובד מקסימאלית קבועה.
נבטא את זמן התנועה מפונקציית מקום זמן המתאימה לתנועה בתאוצה קבועה, נתייחס לציר שראשיתו בנקודת תחילת התנועה וכיוונו כלפי מטה:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»Y«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»*«/mo»«/mrow»«/mfrac»«/msqrt»«/mstyle»«/math»
נמצא את זמן התנועה המינימאלי והמקסימאלי:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mi mathvariant=¨bold¨»min«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»Y«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»g«/mi»«msub»«mo mathvariant=¨bold¨»*«/mo»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»7«/mn»«/msup»«/mrow»«mn mathvariant=¨bold¨»10«/mn»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»414«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»21«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»Y«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»g«/mi»«msub»«mo mathvariant=¨bold¨»*«/mo»«mi mathvariant=¨bold¨»min«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»7«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»828«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»42«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«/mstyle»«/math»
זמן תנועת הגוף גדול מ 1,414.21 שניות , וקטן מ 2,828.42 שניות.
1. لم يتطلب حساب
متوسط زمن الحركة، يكفي الحد السفلي والعلوي لزمن السقوط كإجابة نهائية.
2. من الخطأ عمل
متوسط حسابي بسيط (مجموع زمني الحد العلوي والسفلي مقسومًا على 2) ، لأن التسارع
لا يتغير بوتيرة ثابتة.
3. الأداة
الوحيدة المتاحة في الحركة مع تسارع الجاذبية المتغير هي حفظ الطاقة، ولكن في اعتبارات الطاقة لا يتم
التعامل بزمن الحركة.
2. לא נכון לעשות ממוצע חשבוני פשוט (סכום זמני הגבול חלקי 2) , מכיוון שהתאוצה לא משתנה בקצב קבוע.
3.
______________________________________________________________________________________

______________________________________________________________________________________
...
سرعة اصطدام الجسم بسطح الكوكب مساوية لعشرة آلاف متر في الثانية.
حفظ الطاقة الميكانيكية الكلية.
قوة الجاذبية فقط هي التي تعمل على الجسم ، لذلك يتم حفظ الطاقة الميكانيكية. نكتب معادلة حفظ الطاقة الميكانيكية.
نظرًا لأن الجسم يتحرك بتسارع جاذبية متغير ، سنكتب معادلة حفظ الطاقة باستخدام طاقة وضع الجاذبية.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»KA«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨»KB«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mfenced mathcolor=¨#0000FF¨»«mfrac»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfenced mathcolor=¨#0000FF¨»«mfrac»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mfrac»«/mfenced»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mspace linebreak=¨newline¨»«/mspace»«mfenced mathcolor=¨#0000FF¨»«mfrac»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfenced mathcolor=¨#0000FF¨»«mfrac»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mfrac»«/mfenced»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msup mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced»«mrow»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/mrow»«/mfenced»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«/math»
نستخدم التعبير عن كتلة الكوكب من القسم أ. نعوّض تعبير الكتلة في تعبير السرعة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mspace linebreak=¨newline¨»«/mspace»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced»«mrow»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/mrow»«/mfenced»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»*«/mo»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»G«/mi»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced»«mrow»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/mrow»«/mfenced»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»*«/mo»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«/menclose»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced»«mrow»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/mrow»«/mfenced»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»*«/mo»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced»«mrow»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/mrow»«/mfenced»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mfenced»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»7«/mn»«/msup»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced»«mrow»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»7«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mrow»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»7«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»7«/mn»«/msup»«/mrow»«/mfrac»«/mrow»«/mfenced»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»15«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced»«mrow»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/msup»«/mrow»«/mfenced»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»15«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#160;«/mo»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»000«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
لذلك ، فإنّ سرعة اصطدام الجسم بسطح الأرض عشرة آلاف متر في الثانية.
מכיוון שהגוף נע בתאוצת כובד משתנה, נכתוב את משוואת שימור האנרגיה בעזרת אנרגיה פוטנציאלית כבידתית.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»KA«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨»KB«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mfenced mathcolor=¨#0000FF¨»«mfrac»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfenced mathcolor=¨#0000FF¨»«mfrac»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mfrac»«/mfenced»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mspace linebreak=¨newline¨»«/mspace»«mfenced mathcolor=¨#0000FF¨»«mfrac»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfenced mathcolor=¨#0000FF¨»«mfrac»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mfrac»«/mfenced»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msup mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced»«mrow»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/mrow»«/mfenced»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«/math»
נשתמש בביטוי מסת הכוכב מסעיף א'. נציב את ביטוי המסה בביטוי המהירות:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mspace linebreak=¨newline¨»«/mspace»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced»«mrow»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/mrow»«/mfenced»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»*«/mo»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»G«/mi»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced»«mrow»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/mrow»«/mfenced»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»*«/mo»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«/menclose»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced»«mrow»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/mrow»«/mfenced»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»*«/mo»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced»«mrow»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«/mfrac»«/mrow»«/mfenced»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mfenced»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»7«/mn»«/msup»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced»«mrow»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»7«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mrow»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»7«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»7«/mn»«/msup»«/mrow»«/mfrac»«/mrow»«/mfenced»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»15«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced»«mrow»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/msup»«/mrow»«/mfenced»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»15«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#160;«/mo»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»000«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
לכן, מהירות פגיעת הכדור בכוכב גודלה עשר אלף מטר לשנייה.
من الممكن حساب كتلة الكوكب، واستخدام قيمتها من القسم
الأول وهكذا يمكن أن نوفر من العمليات الجبرية.
______________________________________________________________________________________