حلول التدريبات العملية الجاذبية - ديناميكا (دون الطاقة)
4. أ.4- تسارع الجاذبية على ارتفاع h فوق سطح الكرة الأرضية.
تؤثر على الجسم فقط قوة الجاذبية العامة. نشير إلى هذه القوة بـ Fg.
نرسم مخطط للقوى المؤثرة على الجسم:
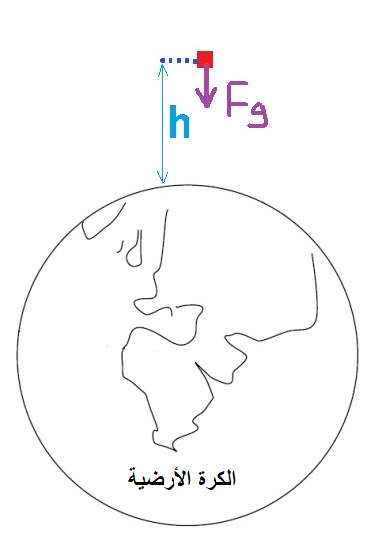
نكتب معادلة الحركة ، نظرًا للبعد الكبير، يختلف التسارع عن تسارع الجاذبية على سطح الأرض.
نشير إلى هذا التسارع بواسطة *g:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«mfenced»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»h«/mi»«/mrow»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
لذلك فإن التعبير عن تسارع الجاذبية على ارتفاع h فوق سطح الأرض هو:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»*«/mo»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mrow»«msup»«mrow»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»h«/mi»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/menclose»«/math»
من التعبير يمكن ملاحظة أنه كلما زاد الارتفاع h ، كلما كان تسارع الجاذبية *g أصغر.
ملاحظات هامة:
1. من التعبير يمكن ملاحظة أنه كان h مهمل نسبة لـ RE ، فإن تسارع الجسم هو g.
2. فقط في اللانهاية يكون تسارع الجاذبية بسبب الكرة الأرضية صفر. رواد الفضاء في الفضاء يسبحون لأنهم يتحركون في حركة قمر اصطناعي داخل مكوك دفع ساتلي. ليس لأنهم وصلوا إلى مكان تساوي فيه تسارع الجاذبية صفرًا.