حلول التدريبات العملية - حركة دائرية منتظمة
8. قطعة نقدية ملقاة على قرص اسطواني 1- Vmax
تؤثر ثلاث قوى على القطعة النقدية: القوة العمودية وقوة الجاذبية وقوة الاحتكاك الساكن. كما هو موضح في الشكل التالي:
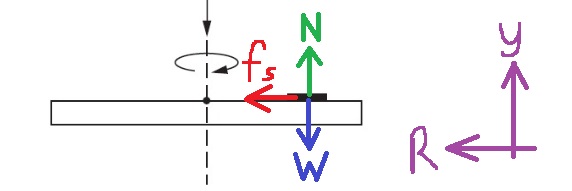
القوة الجاذبة نحو مركز الدوران هي قوة الاحتكاك الساكن، نكتب معادلات الحركة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»f«/mi»«msub»«mi mathvariant=¨bold¨»s«/mi»«mrow/»«/msub»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/menclose»«mspace linebreak=¨newline¨/»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«/menclose»«/math»
لتطوير تعبير لأقصى سرعة ممكنة لحركة القطعة النقدية على القرص الاسطواني (بأي سرعة أكبر يتم "رمي" العملة من اللوحة). سوف نشير إلى حالة عتبة الحركة ، وهي الحالة التي تكون فيها قوة الجاذبية هي أقصى قوة احتكاك ساكن.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»s«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
نُعوّض العمودية من معادلة الحركة العمودية في معادلة الحركة نحو المركز ونعبر عن السرعة القصوى:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msup»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«/math»
لذلك ، فإن تعبير السرعة القصوى هو:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨26px¨»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/msqrt»«/menclose»«mspace linebreak=¨newline¨/»«/mstyle»«/math»