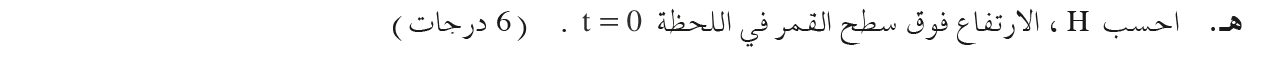1. 2020,1- هبوط مسبار على سطح القمر
______________________________________________________________________________________
...
السقوط الحر هي حركة بتأثير قوة الجاذبية فقط.
في الفيزياء يتم دراسة العديد من المصطلحات، يجب فهم
معنى كل مصطلح.
السقوط الحر هي حركة تحت تأثير قوة الجاذبية فقط.
في كل
حركة على سطح الكوكب، تعمل قوة الجاذبية، في حركات مختلفة يمكن أن تعمل قوى
مختلفة.
السقوط
الحر هي الحركة الأكثر حرية، وهي الحركة التي تعمل فيها قوة الجاذبية فقط.
נפילה חופשית היא התנועה הכי חופשית, תנועה שבה רק כוח הכובד פועל.
______________________________________________________________________________________

______________________________________________________________________________________
...
تعمل قوة الجاذبية دائمًا، بدءًا من حركة المسبار في
الثواني العشر الأولى ، يمكنك معرفة ما إذا كانت قوة المحرك تعمل أيضًا.
يتحرك
المسبار لأسفل وتكون سرعته سالبة، ومن هنا يكون اتجاه محور الحركة نحو الأعلى.
في
الثواني العشر الأولى، يتحرك المسبار إلى أسفل بسرعة قيمتها المطلقة آخذة بالنقصان، حتى يتوقف.
في
الثواني العشر الأولى، تعمل القوة المحصّلة نحو الأعلى لذلك، في هذه الفترة،
تعمل قوة المحرك نحو الأعلى، وتكون أكبر من قوة الجاذبية.
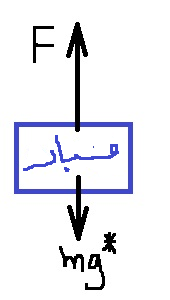
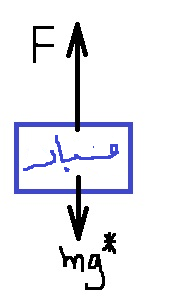
نرسم مخطط القوى:
בעשר השניות הראשונות, הגשושית נעה כלפי מטה במהירות הולכת וגדלה (הולכת וקטנה בערכה המוחלט) , עד לעצירה.
במשך עשר השניות הראשונות הכוח השקול פועל כלפי מעלה. לכן פועל בזמן זה כוח המנוע כלפי מעלה ,והוא גדול מכוח הכובד.
נערוך תרשים כוחות:
1. لا ينص السؤال بشكل صريح متى يتم تشغيل المحرك، لكن يمكن فهم ذلك من خلال
الحركة الموضّحة في الرسم البياني.
2. القوة التي يعملها المحرك
أكبر من قوة الجاذبية ، من المهم أن يكون طول المتجّه الذي يصف قوة المحرك أكبر من
طول متجّه قوة الجاذبية.
3. من الأصح أن نُشير إلى قوة
الجاذبية المؤثرة على سطح القمر بـ *mg وليس بـ W.
2. הכוח שהמנוע מפעיל גדול מכוח הכובד , חשוב שהווקטור המתאר את כוח המנוע יהיה יותר גדול מווקטור כוח הכובד.
3. יותר נכון לסמן את כוח הכובד הפועל על פני הירח ב *mg ולא ב W.
______________________________________________________________________________________

______________________________________________________________________________________
...
مقدار القوة التي يعملها المحرك 601.88 نيوتن.
وفقًا لمخطط القوى من القسم السابق، يمكن كتابة معادلة الحركة ويمكن بواسطتها أن نُعبّر عن قوة المحرك.
نكتب معادلة الحركة ونعبّر منها عن قوة المحرك :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»*«/mo»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/math»
لإيجاد قوة المحرك ، نجد التسارع من ميل الرسم البياني في الثواني العشر الأولى:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»-«/mo»«mstyle mathvariant=¨bold¨»«mrow»«mo»(«/mo»«mo»-«/mo»«mn»20«/mn»«mo»)«/mo»«/mrow»«/mstyle»«/mrow»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»20«/mn»«mn mathvariant=¨bold¨»10«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
نعوّض قيمة التسارع في تعبير القوة ونجد قوة المحرك:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»*«/mo»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»164«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»601«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»88«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/math»
لذلك ، يعمل المحرك قوة مقدارها 601.88 نيوتن.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»*«/mo»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/math»
כדי למצוא את כוח המנוע , נמצא את התאוצה משיפוע הגרף ,בעשר השניות הראשונות:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»-«/mo»«mstyle mathvariant=¨bold¨»«mrow»«mo»(«/mo»«mo»-«/mo»«mn»20«/mn»«mo»)«/mo»«/mrow»«/mstyle»«/mrow»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»20«/mn»«mn mathvariant=¨bold¨»10«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
נציב את ערך התאוצה , בביטוי הכוח ונמצא את גודל כוח המנוע:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»*«/mo»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»164«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»601«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»88«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/math»
לכן, המנוע מפעיל כוח שגודלו 601.88 ניוטון.
1. يجب إيجاد قوة المحرك ، وليس القوة المحصّلة.
2. إن مرحلة رسم مخطط القوى هي مرحلة قصيرة ولكنها حرجة. لا يمكن كتابة إجابة صحيحة دون رسم مخطط القوى الصحيح أولاً.
هناك طلاب يميلون إلى التقليل من شأن مرحلة رسم مخطط القوى،
3. السرعة سالبة لكن التسارع موجب.
4. يجب إيجاد مقدار القوة ، لذلك ليست هناك حاجة للنظر في اتجاه القوة.
2. שלב עריכת תרשים כוחות הוא שלב קצר, אך קריטי . לא ניתן לכתוב תשובה נכונה בלי לערוך קודם תרשים כוחות נכון.
יש תלמידים הנוטים לזלזל בשלב עריכת תרשים הכוחות, עורך השאלה עוזר לתלמידים כאלו ... והוסיף סעיף מקדים
העוסק בתרשים כוחות .
3. המהירות שלילית , אך התאוצה היא חיובית .
4. יש למצוא את גודל הכוח , לכן אין צורך להתייחס לכיוון הכוח .
______________________________________________________________________________________

______________________________________________________________________________________
...
تصبح سرعة المسبار صفر على ارتفاع 5.01 متر.
الكينماتيكا، الحركة بتسارع ثابت، يمكنك استخراج معطيات الحركة من الرسم البياني المعطى.
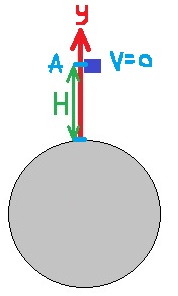
نَصِف حركة المسبار، نسبة لمحور الحركة الذي تكون نقطة أصله على سطح القمر وموجهًا نحو الأعلى ، بالنسبة لهذا المحور ، يكون موقع المجس بالنسبة للمحور مساويًا لارتفاع المسبار فوق سطح القمر.
نحدد النقطة التي تكون فيها سرعة المسبار مساوية لصفر بـ A.
نتطرّق إلى حركة المسبار في السقوط الحر، من النقطة A إلى نقطة الاصطدام على سطح القمر.
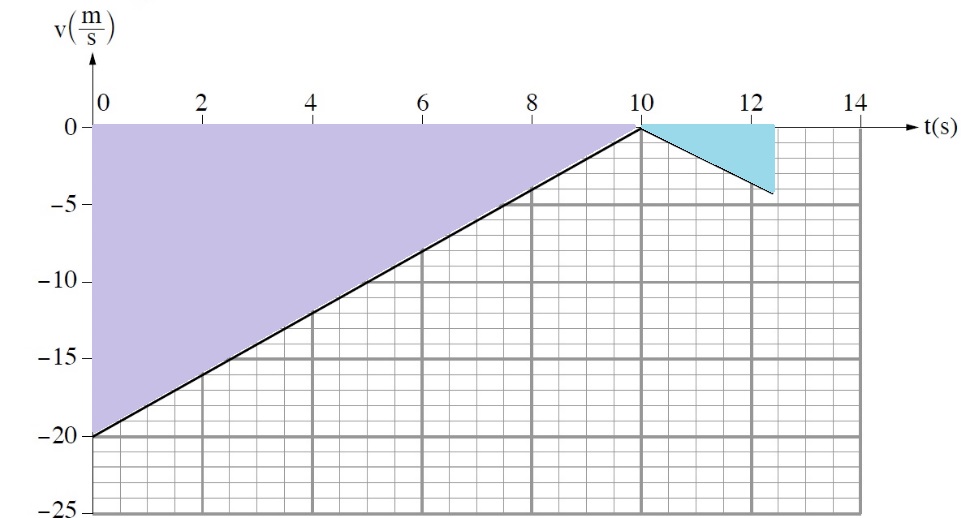
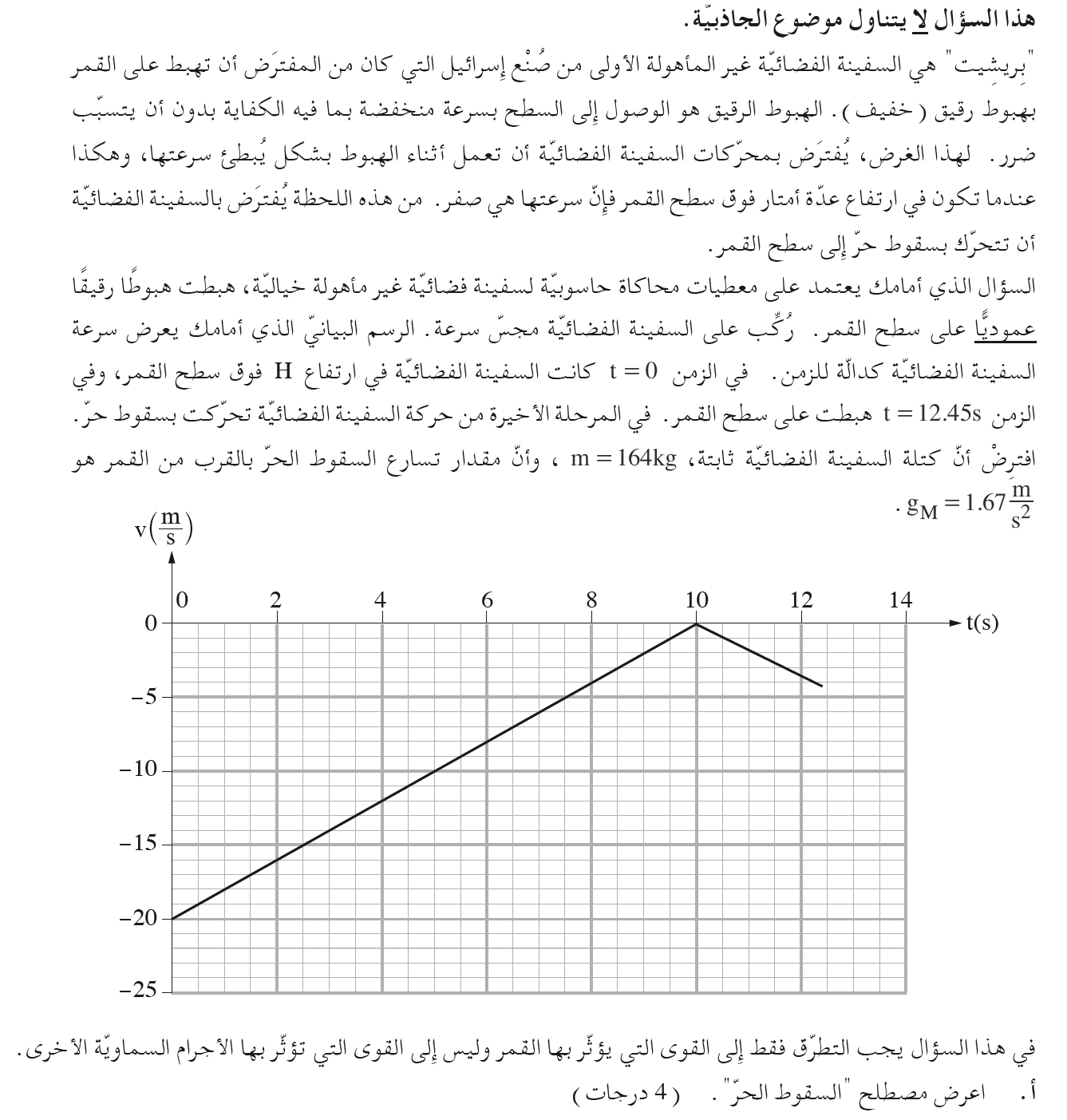
من الرسم البياني يمكن أن نرى أنه في اللحظة t = 10s توقف المسبار. زمن الحركة الكلي للمسبار هو 12.45 ثانية.
لذلك ، فإن زمن حركة المسبار في السقوط الحر هو 2.45 ثانية.
يتحرك المسبار في سقوط حر على سطح القمر، لذا فإن تسارعه الثابت مقداره 1.67m/s2.
نجد ارتفاع النقطة A بمساعدة دالة المكان كدالة للزمن المناسبة للحركة ذات التسارع الثابت:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»45«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»67«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»45«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»67«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»45«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»01«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
لذلك ، أصبحت سرعة المسبار صفر ، على ارتفاع 5.01 متر.
לכן מרגע שהגשושית עצרה ועד שהיא הגיעה לפני הירח עברו 2.45 שניות. בזמן זה הגשושית נעה בנפילה חופשית בתאוצה
שגודלה 1.67 טר לשנייה בריבוע.
הגובה מעל פני הירח שבו התאפסה מהירות הגשושית שווה להעתק הגשושית מהרגע שבו המהירות התאפסה ועד שהגשושית הגיעה לפני הירח .
נתאר את תנועת הגשושית , ביחס לציר שראשיתו בנקודה בה המהירות התאפס וכיוונו כלפי מטה.
נמצא את העתק התנועה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»67«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»45«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»01«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
לכן ,הגובה בו התאפסה מהירות הגשושית היא 5.01 מטר.
1. خلال الـ 12.45 ثانية ، تتغير السرعة ، لكن اتجاه حركة المسبار لا يتغير، واتجاه الحركة دائمًا نحو الأسفل.
2. يتحرك المسبار لأسفل، وسرعته سالبة، وبالتالي يكون اتجاه المحور الموصوف في السؤال نحو الأعلى.
لم يتم تحديد موقع بداية المحور ، يمكن تحديد بداية المحور في أي نقطة، من الأفضل تحديد بداية المحور على السطح.
بحيث تكون قيمة الموقع بالنسبة للمحور مماثلة لارتفاع المسبار فوق السطح.
3. يمكن إيجاد الإزاحة حسب المساحة المحصورة بين الدالة والمحور الزمني من اللحظة t = 10s إلى اللحظة t = 12.45s. هذه الإزاحة تساوي القيمة المطلقة للارتفاع المطلوب.
4. يحتوي السؤال على معطيات غير فيزيائية، ومعطيات ليست لها صلة بالأسئلة. من ناحية أخرى، لا يتم تقديم المعطيات الأكثر صلة لم يتم عرضها بشكل واضح،
على سبيل المثال ، لم يتم تحديد زمن الحركة البالستية بشكل مباشر، فهي تقول أن زمن الحركة الكلي هو 12.45 ثانية ، ونرى في الرسم البياني
المسبار توقف في اللحظة t = 10s. من هاتين الحقيقتين يجب إيجاد زمن الحركة البالستية.
جزء من التحدي هو استخراج المعطيات الهامة، وهذا هو نمط جزء كبير من الأسئلة. لتتمكن من استخراج جميع المعطيات المهمة، يوصى بقراءة السؤال مرة أخرى. وثالثا ، إذا لزم الأمر ...
אך כיוון תנועת הגשושית לא משתנה, כיוון התנועה הוא תמיד כלפי מטה.
2. כיוון הציר המתואר בשאלה הוא כלפי מעלה , ביחס לציר זה ההעתק התנועה מרגע העצירה ועד לפגיעה בקרקע הוא שלילי ,
אך הגובה הוא חיובי. נוח להגדיר ציר חדש לסעיף זה , כפי שמופיע כאן בפתרון המלא.
3. ניתן למצוא את ההעתק התנועה מהשטח התחום בין הפונקציה לציר הזמן מרגע t=10s ועד לרגע t=12.45s.
______________________________________________________________________________________
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»H«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»105«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»m«/mi»«/math»
الارتفاع المطلوب يساوي الإزاحة الكلية ، في الرسم البياني للسرعة، تكون الإزاحة مساوية للمساحة المحصورة بين الدالة والمحور الزمني.
ارتفاع المسبار في اللحظة t = 0s يساوي مقدار إزاحة المسبار خلال كل 12.45 ثانية. هذه الازاحة مساوية لمساحة المحصورة بين الدالة والمحور الزمني.
نتطرّق الى حركتين: الحركة الأولى حركة تحت تأثير قوة المحرك في الثواني العشر الأولى. وحركة ثانية حركة بالستية لمدة 2.45 ثانية.
نُشير إلى المنطقتين في الرسم البياني:
مقدار إزاحة الحركة البالستية 5.01 متر.
نجد إزاحة الحركة الأولى من المساحة المحصورة بين المحور الزمني والدالة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mstyle mathvariant=¨bold¨»«mrow»«mo»(«/mo»«mo»-«/mo»«mn»20«/mn»«mo»)«/mo»«/mrow»«/mstyle»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
ارتفاع المسبار في اللحظة t = 0s يساوي مجموع الإزاحات:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»H«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»y«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»y«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»01«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»105«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
لذلك يكون ارتفاع المسبار H لحظة بداية الحركة: 105.1 متر.
طريقة أخرى :
نتطرّق إلى حركة المسبار الأولى، ونشير إلى موقع المسبار في اللحظة t = 0s بالنقطة M.
نصف الحركة من النقطة M إلى النقطة A. نسبة لهذا المحور الذي تكون نقطة أصله بالسطح وموجهًا نحو الأعلى.
في هذه الحركة، يتحرك المسبار بتسارع نحو الأعلى مقداره 2 متر لكل ثانية مربعة.
من خلال الرسم البياني نلاحظ أن الحركة تستمر لمدة 10 ثوان حتى الموقع 5.01 متر.
نستخدم تعبير المكان كدالة للزمن المناسبة للحركة بتسارع ثابت:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»01«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»01«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»105«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»01«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
الارتفاع H فوق سطح القمر في اللحظة t = 0s هو 105.1 متر.
1.خلال جزء من الزمن في الرسم البياني تكون فيه الدالة تصاعدية وفي جزء آخر تكون فيه الدالة تنازلية، لكن المسبار يتحرك دائمًا نحو الأسفل.
2. يتحرك المسبار بحركتين مختلفتين، فلا يمكنك استخدام دالة واحدة لإيجاد الإزاحة الكلية.
يجب استخدام دالتين ، فمن الأنسب حساب المساحة الكلية بين الدالة والمحور الزمني.
3. في الكينماتيكا، لا يوجد للارتفاع معنى فيزيائي، يوجد معنى للموقع والإزاحة ،عليك فهم معاني الموقع الإزاحة والارتفاع.
وبناءً عليه جد الارتفاع.
4. فيما يتعلق بالمحور الموجّه لأعلى ، تكون الإزاحة سالبة، وهذا يعني أن الجسم يتحرك إلى أسفل.
إشارة الإزاحة ليس لها معنى في حساب الارتفاع ، يجب الأخذ بالحسبان القيمة المطلقة للإزاحة.
______________________________________________________________________________________
______________________________________________________________________________________
...
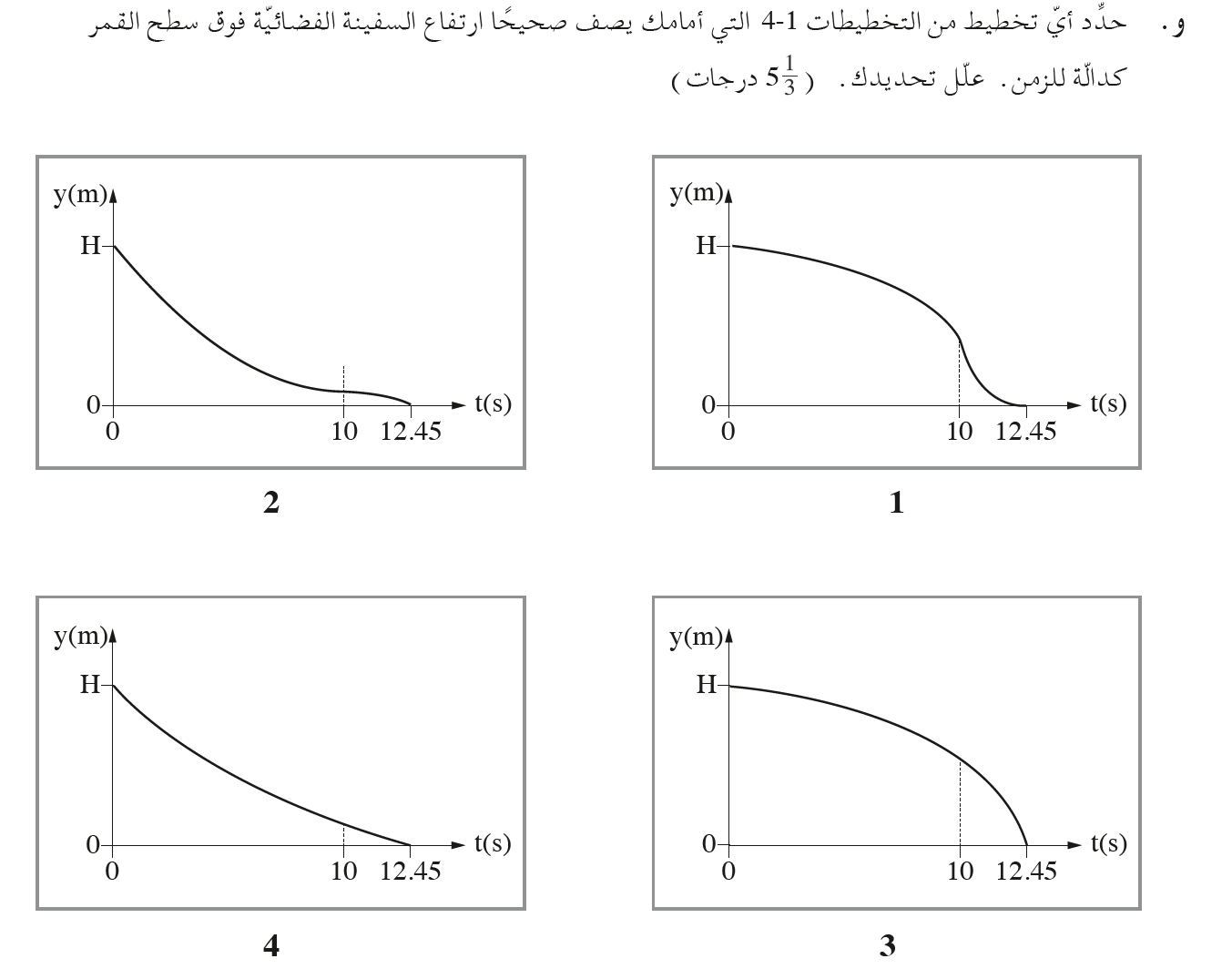
يصف الرسم البياني 2 حركة المسبار بشكل صحيح.
من معرفة الرسم البياني للمكان والزمان ، والتطرق الصحيح إلى محور الحركة.
في الرسم البياني الذي يصف الموقع كدالة للزمن، يكون ميل الرسم البياني مساويًا للسرعة، في اللحظة t = 10s توقف المسبار عن الحركة توقفًا لحظيًا.
فقط في الرسم البياني رقم 2 في اللحظة t = 10s ، يكون الميل صفراً ، وبالتالي فإن الرسم البياني الملائم هو الرسم البياني 2.
רק בגרף מספר 2 ברגע t=10s השיפוע הוא אפס, לכן הגרף המתאים הוא גרף 2.
לכן השיפוע של הגרף צריך להיות אפס.
התרשים היחיד שבו המהירות היא אפס ברגע t=10s הוא תרשים 2, לכן תרשים 2 מתאר נכון את גובה הגשושית בתלות בזמן.
1. يتوقف المحرك عن العمل عندما تُصبِح سرعته مساوية لصفر، وتبدأ الحركة البالستية من السكون.
لذلك ، فإن توقف تشغيل المحرك غير ظاهر في الرسم البياني.
2. يتم الإشارة إلى اللحظة t = 10s في كل دالة ، ويتم الإشارة لهذه اللحظة لأنها مهمة لحل السؤال.
3. الرسم البياني 1 غير مناسب - بعد اللحظة t = 10s يزداد الميل ، وتتزايد السرعة باستمرار والتسارع موجب - يتوافق مع محصّلة القوى تعمل نحو الأعلى.
ولكن بعد لحظة t = 10s يتحرك المسبار في حركة بالستية ، تعمل القوة المحصّلة نحو الأسفل.
الرسم البياني 3 غير مناسب - لأن الميل دائمًا آخذ بالنقصان، والتسارع سالب - مناسب لقوة لمحصلة قوى تعمل دائمًا في اتجاه الأسفل.
لكن في حركة المسبار الأولى ، تعمل محصلة القوى نحو الأعلى.
الرسم البياني 4 - لا يمكن أن يكون مناسبًا ، فالميل سالب ويتزايد باستمرار ، والسرعة تزداد ، والتسارع موجب. مناسب لمحصلّة قوى
تعمل دائمًا في اتجاه الأعلى.
لكن في حركة المجس الثاني ، يتحرك المسبار في حركة بالستية لأن القوة المحصّلة تعمل نحو الأسفل.
4. يصف الرسم البياني الارتفاع ، والارتفاع ليس مقدار فيزيائي في الكينماتيكا . يجب التطرُق إلى المحور الذي نقطة أصله في السطح واتجاهه نحو الأعلى .
______________________________________________________________________________________