حلول ومنتديات لألبوم الحلول - الديناميكا في خط مستقيم
30. 1997,1-سطح مائل غير أملس

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
مخطط القوى ، معادلات الحركة ، التعبير عن التسارع من معادلات الحركة ، وإيجاد السرعة في اللحظة t = 5s باستخدام دالة السرعة كدالة للزمن.
لا تتغير القوى المؤثرة على الجسم خلال الثواني الخمس كلها. لذلك ، يتحرك الجسم بتسارع ثابت.
لإيجاد سرعة الجسم بعد 5 ثوانٍ من بدء حركته، نجد تسارعه.
نرسم رسم تخطيطي للقوى المؤثرة على الجسم:
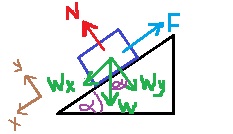
نكتب معادلات الحركة للجسم في اتجاه منحدر السطح بالنسبة للمحور X الموجّه في اتجاه المنحدر للمستوى. والمحور Y في الاتجاه العمودي للمستوى.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨»y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»mg«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«/math»
نعبّر من معادلة الحركة في اتجاه المحور X عن تسارع الجسم:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»mg«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»mg«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»F«/mi»«/mrow»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»30«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
نستخدم تعبير السرعة كدالة للزمن لإيجاد سرعة الجسم في اللحظة t=5s:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfenced mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
بعد 5 ثوانٍ من اللحظة التي تبدأ فيها الحركة ، يتحرك الجسم في مرتقى السطح بسرعة 8 أمتار في الثانية.
1. اتجاه المحور الذي تم اختياره في السؤال هو في اتجاه إلى أسفل. من المهم جدًا المحافظة على إشارات المقادير الفيزيائية ، وفقًا لاتجاه المحور.
2. في معادلة الحركة ، تكون إشارة القوة F سالبة ، واشارة مركّب قوة الجاذبية WX موجبة.
______________________________________________________________________________________

______________________________________________________________________________________
...

وصف حركة الجسم ، وفقًا للمحور المحدّد ، والسرعة الابتدائية المعطاة، والتسارع الذي تم الحصول عليه من معادلة الحركة خلال الثواني الخمس الأولى من الحركة.
يبدأ الجسم في التحرك من سرعة 12 مترًا في الثانية بتسارع سالب قدره «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math» , لمدة 5 ثوان حتى تصل سرعة الجسم «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math» .
نصف حركة الجسم في الرسم البياني للسرعة كدالة للزمن:
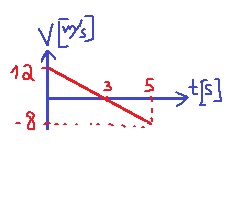
נתאר את תנועת הגוף בגרף מהירות בתלות בזמן:

يوجد نوعان من الرسوم البيانية: الرسم البياني النوعي والرسم البياني الكمي، الرسم البياني النوعي هو رسم بياني لا يحتوي على أي قيم في المحاور، فهو يصف الشكل العام للدالة.
الرسم البياني الكمي هو رسم بياني يحتوي على قيم في المحاور ، حتى في هذا الرسم البياني يكفي للإشارة إلى القيم المهمة فقط.
في الرسم البياني الذي تم رسمه حسب نتائج القياس (جدول نتائج القياس) ، يجب وصف جميع قيم المحور ويجب وضع علامة لكل نتيجة قياس كنقطة على الرسم البياني.
גרף כמותי הוא גרף המכיל את ערכי הצירים ,גם בגרף זה מספיק לציין את הערכים החשובים בלבד.
בגרף הנבנה מתוצאות מדידות (טבלת תוצאות מדידות) , יש לתאר את כל ערכי הצירים ולסמן בהתאם כל תוצאת מדידה כנקודה בגרף.
______________________________________________________________________________________
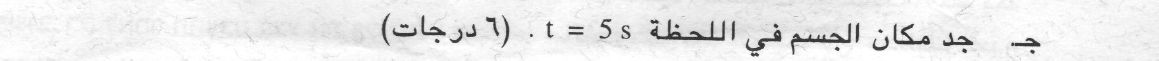
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»10«/mn»«mi mathvariant=¨bold¨»m«/mi»«/math»
استخدام تعبير المكان كدالة للزمن المناسب للحركة بتسارع ثابت، ووصف الحركة بالنسبة للمحور المعطى في السؤال.
نجد موقع الجسم في اللحظة t = 5s بمساعدة تعبير الموقع كدالة للزمن.
نتطرق إلى المحور الموصوف في السؤال.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfenced mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»60«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»50«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
في نهاية الخمس ثوانٍ ، يكون الجسم في نقطة تقع على بعد 10 أمتار أسفل المستوى بالنسبة إلى نقطة بداية حركته. نسبة للمحور المعطى x=10m.
נתייחס לציר המתואר בשאלה.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfenced mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»60«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»50«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
בתום חמש השניות הגוף נמצא בנקודה הממוקמת 10 מטרים במורד המישור יחסית לנקודת תחילת תנועתו.
ביחס לציר הנתון x=10m.
بشكل عام، يمكن وصف الحركة نسبة لأي محور حركة محدّد. في هذه الحالة ، يظهر محور الحركة في السؤال ، يجب وصف الحركة فقط نسبة لهذا المحور.
______________________________________________________________________________________

______________________________________________________________________________________
...
من اللحظة التي يتوقف فيها عمل القوة F ، يتحرك الجسم بتسارع ثابت في اتجاه أسفل المستوى.
يتحرك الجسم في البداية لأعلى بسرعة قيمتها المطلقة آخذة بالنقصان حتى يتوقف توقفًا لحظيًا.
بعد ذلك يتحرك الجسم في اتجاه الانحدار بسرعة آخذة بالازدياد.
בהתחלה הגוף נע כלפי מעלה במהירות הולכת וקטנה בערכה המוחלט עד לעצירה רגעית.
לאחר מכן הגוף נע בכיוון המורד במהירות הולכת וגדלה.
لوصف مسار حركة الجسم، يجب أن نُشير إلى موقع الجسم في اللحظة التي يتوقف فيها عمل القوة، ونوع الحركة التي يتحرك فيها الجسم بعد توقف القوة، والتغير في اتجاه الحركة.
تتسبب القوة F في تحريك الجسم بتسارع نحو الأعلى، في اللحظة t = 5s يتحرك فيها الجسم لأعلى المستوى بسرعة 8 أمتار في الثانية.
في اللحظة t = 5s ، توقف القوة F عملها، القوة الوحيدة المؤثرة على الجسم في اتجاه المحور X هي مركّب الجاذبية WX ، يتحرك الجسم بتسارع ثابت نحو الأسفل.
لذلك، من اللحظة t = 5s ، تنخفض السرعة في قيمتها المطلقة حتى يتوقف الجسم، وبعد التوقف يستمر الجسم في التحرك نحو الأسفل بنفس التسارع وبسرعة آخذة بالازدياد.
يصف الرسم البياني التالي مسار حركة الجسم بشكل عام ، بمساعدة رسم تخطيطي لأعقاب الجسم في فترات زمنية محددة ، من اللحظة t = 5s أثناء صعوده وهبوطه ، تصف النقاط الحمراء موقع الجسم أثناء صعوده ، وتصف النقاط الخضراء موقع الجسم أثناء هبوطه.
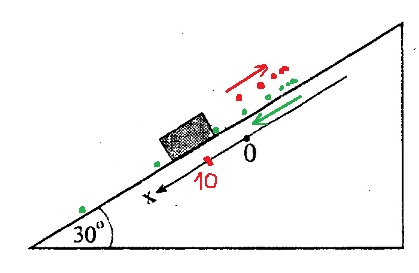
ברגע t=5s הכוח F מפסיק את פעולתו הכוח היחיד הפועל על הגוף בכיוון ציר X הוא רכיב כוח המשיכה WX , הגוף נע בתאוצה קבועה כלפי מטה .
לכן מרגע t=5s, המהירות הולכת וקטנה בערכה המוחלט עד שהגוף נעצר , לאחר עצירתו הגוף ממשיך לנוע באותה התאוצה ,והוא נע כלפי מטה במהירות הולכת וגדלה.
התרשים הבא מתאר את מסלול תנועת הגוף באופן כללי , בעזרת תרשים עקבות המסומנות בכל פרק זמן קבוע, מרגע t=5s בעלייתו ובירידתו , הנקודות האדומות מתארות את מיקום הגוף בעלייתו , והנקודות הירוקות מתארות את מיקום הגוף בירידתו.

1. من اللحظة التي توقفت فيها القوة F عن التأثير، يتحرك الجسم في رمي بمرتقى السطح على غرار الرمي العمودي لسطح الأرض.
2. من اللحظة التي يتوقف فيها عمل القوة F ، يتحرك الجسم بنفس التسارع ، سواء عندما يتحرك لأعلى أو لأسفل (وكذلك عند نقطة التوقف).
3. للإجابة على هذا السؤال بشكل صحيح ، يجب أن تفهم معنى التسارع ومعنى السرعة.
2. מרגע הפסקת פעולת הכוח F , הגוף נע באותה התאוצה, גם כאשר הוא נע כלפי מעלה , וגם כאשר הוא נע כלפי מטה, (וגם בנקודת העצירה).
______________________________________________________________________________________