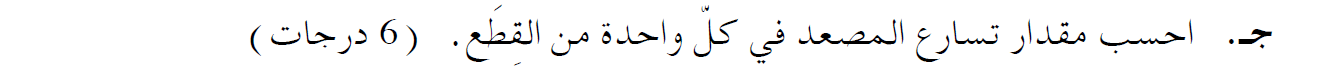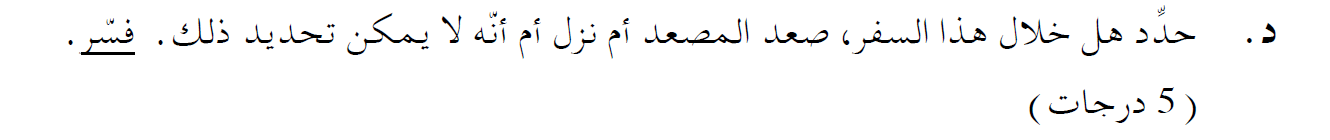8. 2015,3- الوزن الخيالي داخل مصعد
______________________________________________________________________________________
...
(2) القوة العمودية التي يؤثر بها الميزان على سامية.
من مبادئ الوزن الوهمي، قراءة الميزان وهي القوة التي يشغّلها الجسم على الميزان، ويُشار إلى هذه القوة بالحرف "N.
القوة العمودية N هي القوة التي يشغّلها الميزان على الجسم. من القانون الثالث ، N تساوي في المقدار للقوة 'N.
כוח הנורמל N , הוא הכוח שהמאזניים מפעילים על הגוף . מהחוק השלישי N שווה בגודלו ל 'N.
(2) القوة العمودية التي يشغّلها الميزان على سامية.
هذا السؤال مضلل بعض الشيء ، والغرض من الميزان هو قياس قوة الجاذبية المؤثرة على سامية، لذلك يمكن القول أن قراءة الميزان هي قوة الجاذبية.
أنا مقتنع بأن العديد من الطلاب الذين لا يفهمون جيدًا موضوع الوزن الخيالي، اختاروا إجابة غير صحيحة لمجرد أن السؤال مضلل. ونظرًا لعدم وجود حاجة للتفسير ، إذا لم يفسروا فلن يحصلوا على درجة جزئية أيضًا .
لذلك، على الرغم من أنه مطلوب الاختيار دون تفسير، فمن الأفضل في مثل هذه الحالة التفسير والكتابة أن الغرض من الميزان بشكل عام هو قياس قوة الجاذبية، عندما تكون القوة المحصّلة في الاتجاه العمودي لا تساوي الصفر ، فإن قراءة الميزان لا تساوي الوزن. وعلى أي حال ، فإن قراءة الميزان في هذه الحالة تمثل دائمًا القوة العمودية.
من الممكن أيضًا وضع دائرة حول الإجابتين 1 و 2. وإضافة تفسير.
لا تخف من كتابة الإجابة الصحيحة التي تكون متأكدًا منها بطريقة مختلفة عن الطريقة التي طُلب منك بها الإجابة عن السؤال.
אם זמן לכתוב נימוק , עדיף לבחור את התשובה הנכונה ולהמשיך הלאה.
2. הכוח 'N שתמי מפעילה על המאזניים ,הוא הכוח המוצג במאזניים, בגלל החוק השלישי גם הכוח N מייצג את הוריית המאזניים. בשאלות העוסקות במשקל מדומה יש להבחין בין N ל 'N . ולנמק בעזרת החוק השלישי של ניוטון.
______________________________________________________________________________________

______________________________________________________________________________________
...
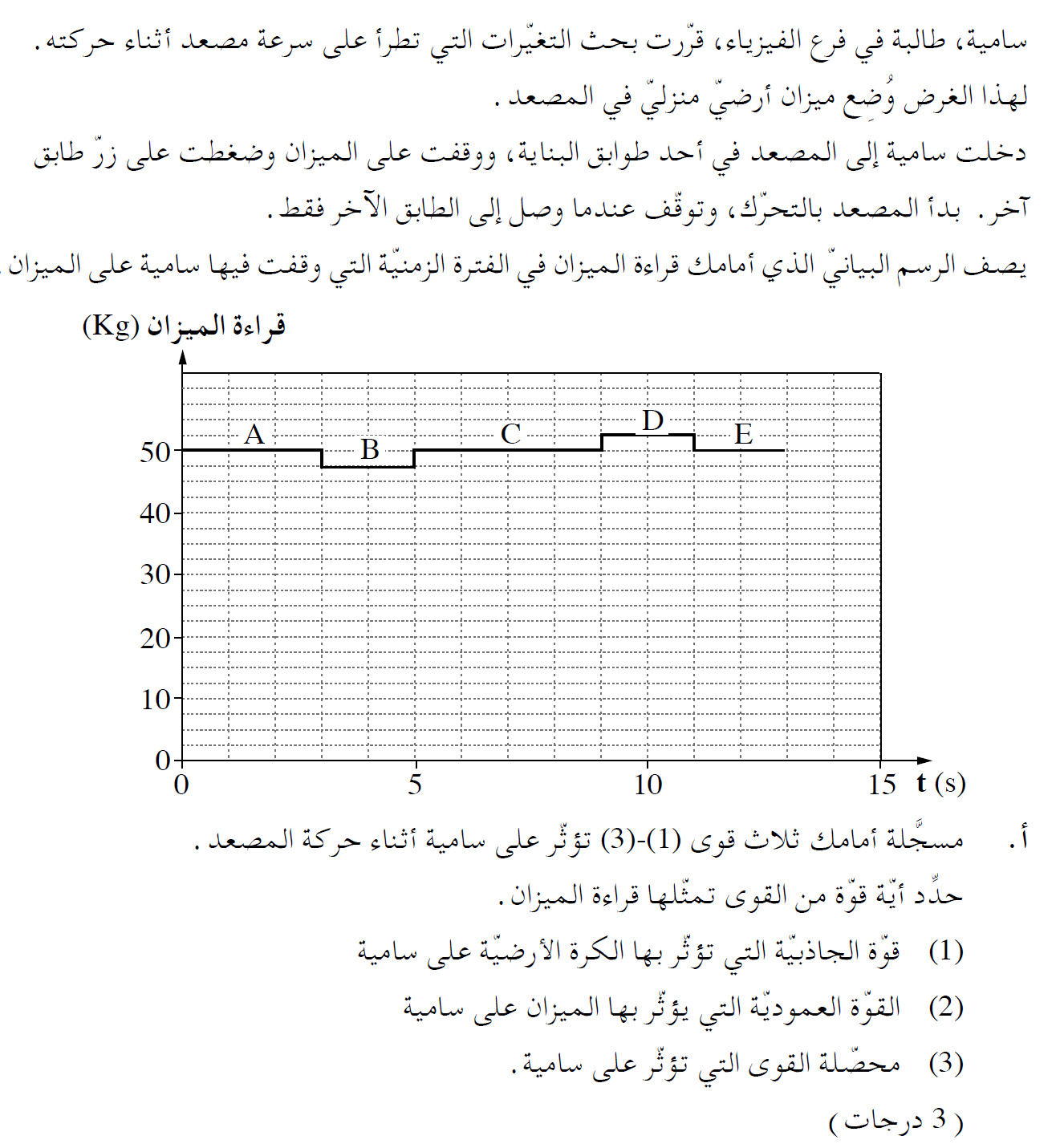
المقطع A- ساكن.
المقطع B- حركة بسرعة متغيرة.
المقطع C- حركة بسرعة منتظمة.
المقطع D- حركة بسرعة متغيرة.
المقطع E- ساكن.
קטע B- תנועה במהירות משתנה.
קטע C- תנועה במהירות קצובה.
קטע D- תנועה במהירות משתנה.
קטע E- מנוחה.
يجب تحديد مراحل الحركة التي تكون فيها قراءة الميزان مساوٍ للوزن الحقيقي.
عندما تكون قراءة الميزان أصغر أو أكبر من الوزن الحقيقي، تكون القوة العمودية أصغر أو أكبر من الوزن - محصلة القوى على سامية تساوي لصفر.
عندما تكون قراءة الميزان مساوٍ للوزن الحقيقي، يجب التمييز بين الحركة بسرعة ثابتة وحالة السكون ، وحتى يتم ذلك يجب فهم الحركة بأكملها.
כאשר הערך המוצג קטן או גדול מהערך האמתי, הנורמל קטן מהמשקל - שקול הכוחות על תמי שונה מאפס.
כאשר הערך המוצג הוא אמתי , יש להבחין בין תנועה במהירות קצובה לבין מנוחה, ההבחנה היא מהבנת כל התנועה.
حركة المصعد هي نفس حركة سامية. من خلال قراءة الميزان ، يمكن فهم كيفية حركة سامية، وبالتالي معرفة حركة المصعد.
سنتعلم من ديناميكيات القوى المؤثرة على سامية حول نوع حركة المصعد ، في كل مقطع:
المقطع A- حالة سكون - هناك مرحلة دخلت فيها سامية المصعد ووقفت على الميزان قبل الضغط على الزر.
هذه المرحلة هي مرحلة السكون، لذلك في المرحلة الأولى تقف سامية على الميزان في حالة سكون، والمصعد لا يتحرك.
المقطع B- الحركة بسرعة متغيرة - قراءة الميزان أصغر من الوزن الحقيقي. في هذه المرحلة تكون القوة العمودية على سامية أقل من وزنها.
القوة المحصّلة المؤثرة على سامية نحو الأسفل. تسارع سامية نحو الأسفل. وكذلك المصعد.
المقطع C- الحركة بسرعة ثابتة - قراءة الميزان في هذه المرحلة. نفس قراءة الميزان في المرحلة الأولى ، وبالتالي فإن القوة المحصّلة المؤثرة على سامية تساوي صفرًا.
في نهاية المرحلة الثانية ، في نهاية المقطع B. كان لسامية سرعة. لهذا السبب فإن سامية ستواصل حركتها بهذه السرعة. يتحرك المصعد بسرعة ثابتة.
المقطع D- الحركة بسرعة متغيرة - قراءة الميزان في هذه المرحلة أكبر من قيمة قراءة الميزان في المرحلة الأولى.
القوة العمودية المؤثرة على سامية نحو الأعلى أكبر من وزنها ، سامية تتحرك بتسارع نحو الأعلى، المصعد يتحرك بسرعة متغيرة.
المقطع E- في حالة سكون - قيمة قراءة الميزان هي نفس قيمة قراءة الميزان في المرحلة الأولى، والقوة المحصّلة المؤثرة على سامية مساوية صفر.
يتحرك المصعد في المرحلة B لمدة ثانيتين في تسارع نحو الأسفل. في المرحلة D ، يتحرك المصعد لمدة ثانيتين بنفس التسارع وفي نفس الزمن
نحو الأعلى ، وبالتالي فإن السرعة في نهاية المرحلة D تكون مساوية لنفس السرعة التي كانت عليها في المرحلة A. السرعة صفر.
وبما أن ميزان القوى في المرحلة E يساوي صفرًا ، فإن المصعد سوف يستقر في المرحلة E.
1. على الرغم من أنه من الممكن التطرّق إلى الحركة من أي لحظة نختارها إلى أي لحظة أخرى. تبدأ حركة المصعد عادةً من حالة السكون، وتنتهي أيضًا بحالة السكون.
2. عندما يتحرك الجسم في سلسلة من الحركات المختلفة ، فإن التسارع ومحصلة القوى يتعلقان فقط على القوى التي تعمل في تلك المرحلة ، والسرعة في كل مرحلة تتعلق على السرعة في نهاية المرحلة السابقة.
3. حركة المصعد هي حركة عمودية ولكنها ليست حركة بالستية ، المصعد لا يتحرك تحت تأثير الجاذبية وحدها. يمكن أن يتحرك في تسارع أيًا كان.
2.כאשר גוף נע ברצף של תנועות שונות, התאוצה והכוח השקול תלויים רק בכוחות הפועלים באותו שלב , המהירות בכל שלב תלויה במהירות בסוף השלב הקודם.
3. תנועת המעלית היא תנועה אנכית , אך היא לא תנועה בליסטית, המעלית לא נעה בהשפעת כוח הכובד בלבד. לתאוצתה יכול להיות ערך כלשהו.
______________________________________________________________________________________
______________________________________________________________________________________
...
نسبة لمحور حركة نحو الأسفل، فإن التسارع هو:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»c«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»D«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»c«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»D«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»D«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mrow»«/mstyle»«/math»
قراءة الميزان بالكيلو غرام ، يمكن إيجاد القوة العمودية بحسب قراءة الميزان، ووفقًا للقوة العمودية ومقدار الوزن الحقيقي يمكن إيجاد التسارع في كل مرحلة باستخدام القانون الثاني لنيوتن.
يُشير الميزان إلى وحدات الكيلوغرام ، لذا فهو يُشير إلى كتلة سامية، وليس إلى وزنها، ووزنها أكبر بعشرة أضعاف، والقوة العمودية أكبر بعشر مرات من القيمة المعروضة.
تتعلّق إشارة التسارع على اتجاه المحور الذي تم اختياره، وقد تم اختيار محور نحو الأسفل.
في المرحلة A - سامية موجودة في حالة سكون، قراءة الميزان 50 كيلوغرام ووزنها 500 نيوتن والقوة العمودية مقدارها 500 نيوتن ومحصلة القوى تساوي صفرًا:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mrow»«/mstyle»«/math»
في المرحلة B- قراءة الميزان 47.5 كغم, القوة العمودية التي تعمل على سامية مساوية 475 نيوتن، وزن سامية لا يتغير، ويبقى 500 نيوتن. نحسب تسارعها, نسبة للمحور المحدّد:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#931;«/mi»«mi mathvariant=¨bold¨»F«/mi»«/mrow»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»500«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»475«/mn»«/mrow»«mn mathvariant=¨bold¨»50«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»25«/mn»«mn mathvariant=¨bold¨»50«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/math»
في المرحلة C - قراءة الميزان 50 كغم. القوة العمودية التي تعمل على سامية مساوية 500 نيوتن، ومساوٍ لوزن سامية، محصلة القوى التي تعمل على سامية مساوية لصفر.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/math»
في المرحلة D - قراءة الميزان 52.5 كغم. القوة العمودية التي تعمل على سامية مساوية 525 نيوتن، وزن سامية لا يتغير، ويبقى 500 نيوتن.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»D«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#931;«/mi»«mi mathvariant=¨bold¨»F«/mi»«/mrow»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»500«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»525«/mn»«/mrow»«mn mathvariant=¨bold¨»50«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»25«/mn»«/mrow»«mn mathvariant=¨bold¨»50«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/math»
في المرحلة E - قراءة الميزان 50 كغم. القوة العمودية التي تعمل على سامية مساوية 500 نيوتن، ومساوٍ لوزن سامية، محصلة القوى التي تعمل على سامية مساوية لصفر.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/math»
סימן התאוצה תלוי בכיוון הציר הנבחר,נבחר ציר שכיוונו כלפי מטה.
בשלב A - תמי נמצאת במנוחה , הורית המאזניים 5 ק"ג . משקלה 50 ניוטון , וגודל הנורמל 50 ניוטון, שקול הכוחות שווה לאפס:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mrow»«/mstyle»«/math»
בשלב B- הורית המאזניים 4.75 ק"ג, כוח הנורמל הוא 47.5 ניוטון , משקלה של תמי לא משתנה , הוא נשאר 50 ניוטון. נחשב את תאוצתה, ביחס לציר הנבחר:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#931;«/mi»«mi mathvariant=¨bold¨»F«/mi»«/mrow»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»50«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»47«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«mn mathvariant=¨bold¨»5«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«mn mathvariant=¨bold¨»5«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/math»
בשלב C - הורית המאזניים 5 ק"ג . כוח הנורמל הפועל על תמי גודלו 50 ניוטון , זהה למשקלה של תמי, שקול הכוחות הפועלים על תמי שווה לאפס.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/math»
בשלב D - הורית המאזניים 5.25 ק"ג . כוח הנורמל הפועל על תמי גודלו 52.5 ניוטון , משקלה של תמי נשאר 50 ניוטון.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨»D«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#931;«/mi»«mi mathvariant=¨bold¨»F«/mi»«/mrow»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»50«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»52«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«mn mathvariant=¨bold¨»5«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«mn mathvariant=¨bold¨»5«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/math»
בשלב E - הורית המאזניים 5 ק"ג לכן משקלה 50 ניוטון ,שקול הכוחות הפועלים עליה שווה לאפס: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/math»
1. تتعلق إشارة التسارع باتجاه محور الحركة الذي تم اختياره، ولا يظهر أي محور حركة في السؤال. لكتابة إشارة التسارع ، يجب عليك اختيار محور الحركة الذي سيتم وصف التسارع بالنسبة له.
نظرًا لأنه مطلوب حساب مقدار التسارع ، فمن الممكن كتابة القيمة المطلقة للتسارع. من الأفضل اختيار المحور وكتابة التسارع مع إشارته.
في الأسئلة التي لا يتم فيها تحديد المحور ، فإن إضافة المحور يقلل من الشكوك ، ويقوي ثقتك في حل التمرين ، فلن تحصل على المساعدة في حالة عدم وجود محور ، فلديك الحق في إضافته.
في بعض الأحيان يجب عليك إضافة المحور.
يمكنك اختيار محور الحركة الموجّه نحو الأعلى ، في هذه الحالة ، يجب عكس إشارة التسارع. قيمة التسارع لن تتغير.
2. من الممكن أن نكتب بإيجاز أنه في المراحل التي يستقر فيها المصعد أو يتحرك بسرعة ثابتة ، لا يوجد تغيير في السرعة وبالتالي لا يوجد تسارع. واحسب التسارع فقط في المرحلتين B و D.
מכיוון שיש לחשב את גודל התאוצה , אפשר לכתוב את הערך המוחלט של התאוצה. עדיף לקבוע ציר ולכתוב את התאוצה עם סימנה.
בשאלות בהן לא מופיע ציר הוספת הציר מקטינה ספקות, מעצימה את הביטחון שלכם בפתרון התרגיל , לא עוזרים לכם כשאין ציר , זכותכם להוסיף אותו .
לפעמים חייבים להוסיף את הציר.
ניתן לבחור ציר תנועה שכיוונו כלפי מעלה , במקרה כזה, סימני התאוצות יהיו הפוכים. ערך התאוצות לא ישתנה.
2. אפשר לכתוב בקצרה שבשלבים בהם המעלית נחה או נעה במהירות קבועה אין שינוי מהירות לכן אין תאוצה. ולחשב את התאוצה רק בשלבים B ו- D .
______________________________________________________________________________________
______________________________________________________________________________________
...
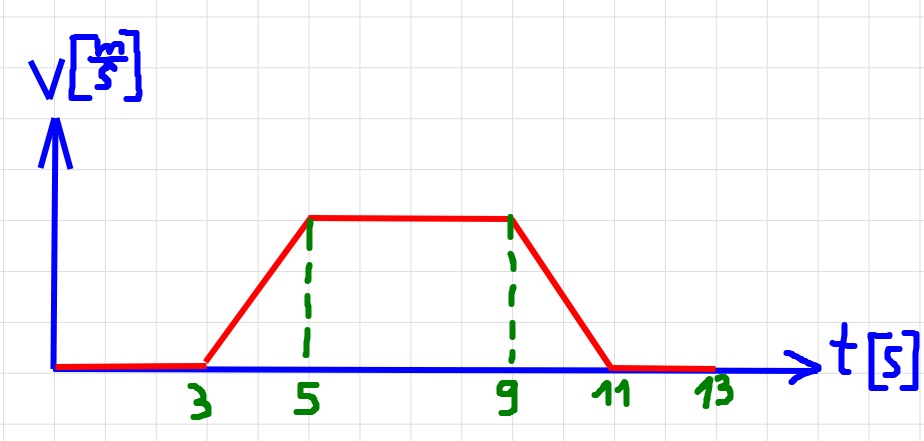
المصعد ينزل .
من قراءة الميزان يمكنك معرفة مقدار واتجاه التسارع ، بمساعدة معطيات الحركة الابتدائية واتجاه التسارع يمكنك معرفة اتجاه الحركة.
في المرحلة الأولى كان المصعد في حالة سكون. في المرحلة الثانية ، يتحرك بتسارع نحو ا لأسفل ، تؤثر محصلة القوى على الجسم نحو الأسفل، وبالتالي يكون اتجاه الحركة لأسفل.
بالنسبة لمحور الحركة - اتجاه المحور نحو الأسفل، في المرحلة الأولى يستقر المصعد. ثم في المرحلة الثانية يتحرك بتسارع موجب. السرعة آخذة بالازدياد ولأن السرعة موجبة يتحرك المصعد في اتجاه المحور لأسفل.
ביחס לציר התנועה - כיוון הציר הוא כלפי מטה , בשלב הראשון המעלית נחה. לאחר מכן בשלב השני היא נעה בתאוצה חיובית. המהירות הולכת וגדלה, מכיוון שהמהירות היא חיובית המעלית נעה בכיוון הציר כלפי מטה.
1. بشكل عام ، بمساعدة اتجاه التسارع ، لا يمكن معرفة اتجاه الحركة.
على سبيل المثال، عندما يتم رمي الجسم لأعلى يتحرك لأعلى ،ثم يتحرك لأسفل ، لكن اتجاه التسارع يكون دائمًا لأسفل.
2. في حالة خاصة (مثل هذه الحالة) عندما يكون الجسم في حالة سكون، واذا عُلِّم اتجاه القوة / التسارع ، يمكن معرفة اتجاه الحركة.
بشكل عام ، فقط اتجاه التسارع لا يشير إلى اتجاه الحركة.
3. بعد تحديد اتجاه الحركة في لحظة واحدة، من الممكن تحديد اتجاه الحركة في أي لحظة كانت.
כך למשל , כאשר גוף נזרק כלפי מעלה. בחל מהזמן הוא נע כלפי מעלה, ובחלק מהזמן הוא נע כלפי מטה, אך כיוון התאוצה תמיד כלפי מטה.
2. במקרה מיוחד , (כמו מקרה זה) כאשר הגוף נמצא במנוחה , ונתון כיוון הכוח/התאוצה ניתן לדעת את כיוון התנועה .
באופן כללי רק כיוון התאוצה לא מעיד על כיוון התנועה.
3. לאחר זיהוי כיוון התנועה ברגע אחד, ניתן לזהות את כיוון התנועה בכל רגע .
______________________________________________________________________________________

______________________________________________________________________________________
...
نسبة لمحور حركة اتجاهه نحو الأسفل:
نسبة لمحور حركة اتجاهه نحو الأسفل ، لأنه عندما يتحرك المصعد ، فإنه يتحرك للأسفل فقط ، وتكون السرعة دائمًا موجبة.
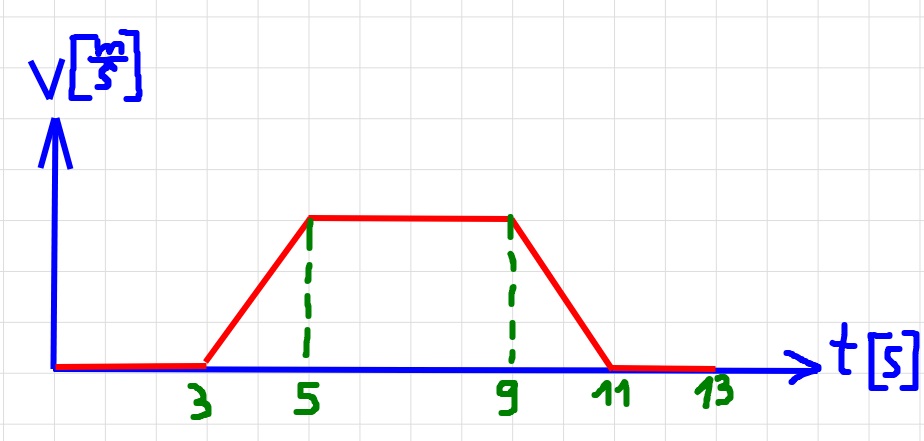
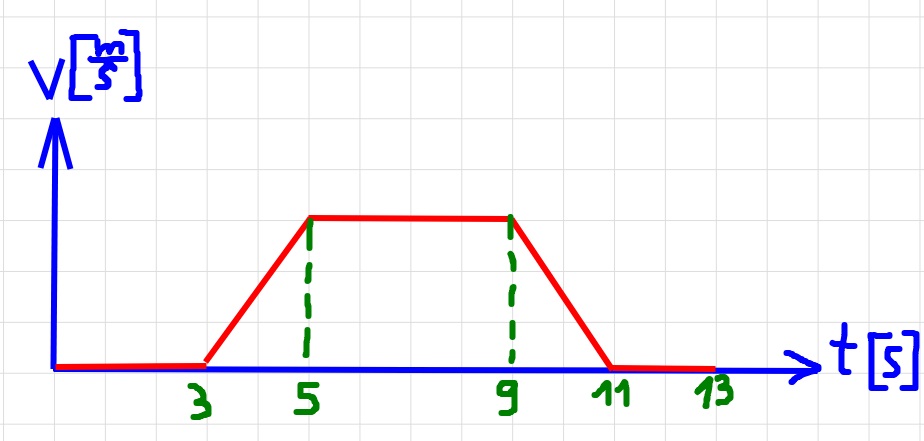
نصف الرسم البياني للسرعة كدالة للزمن، وفقًا لقيم التسارع التي وجدناها في القسم ج ،
בהתאם לערכי התאוצות שמצאנו בסעיף ג' , נתאר את גרף המהירות בתלות בזמן.
יש לתאר את גרף המהירות בתלות בזמן , בהתאם לתאוצה בכל שלב.
نستخدم التسارع الذي وجدناه في القسم ج ، ونصف حركة المصعد بالنسبة للمحور الذي اتجاهه نحو الأسفل.
وفقًا لما ذُكِر في السؤال ، نشير إلى قيم الزمن في الرسم البياني، وليس قيم السرعة:
בהתאם לנאמר בשאלה נציין בגרף את ערכי הזמן, ולא את ערכי המהירות:
1. حسب اتجاه المحور، في الرسم البياني للسرعة كدالة للزمن في هذه الحالة، حتى عندما تكون الدالة تصاعدية، يهبط المصعد.
2. الحل المعروض هنا مناسب للمحور الموجّه نحو الأسفل، ويمكن أيضًا حل هذا السؤال نسبة لمحور موجّه نحو الأعلى. لهذا السبب من المهم تحديد اتجاه المحور.
2. בתרגול השאלה מומלץ למצוא את ערכי המהירויות בגרף, במבחן בגרות הזמן מאוד יקר אם כתוב אינך נדרש ... עדיף לא להשקיע בכך זמן.
______________________________________________________________________________________