حلول التدريبات العملية ديناميكا لجسم واحد

3.3. زاوية ميل السطح عند عتبة الحركة.

نتطرق إلى جسم موجود على عتبة الحركة، حالة تكون فيها قوة الاحتكاك الساكن قصوى: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»fs«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»max«/mi»«/msub»«/mstyle»«/math»

نشير لزاوية ميل السطح في هذه الحالة:  «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/msub»«/mstyle»«/math».

عند بداية الحركة، تعمل على الجسم ثلاث قوى: قوة الجاذبية والقوة العمودية وقوة الاحتكاك الساكن الأقصى. 

نرسم مخطط القوى المؤثرة على الجسم:

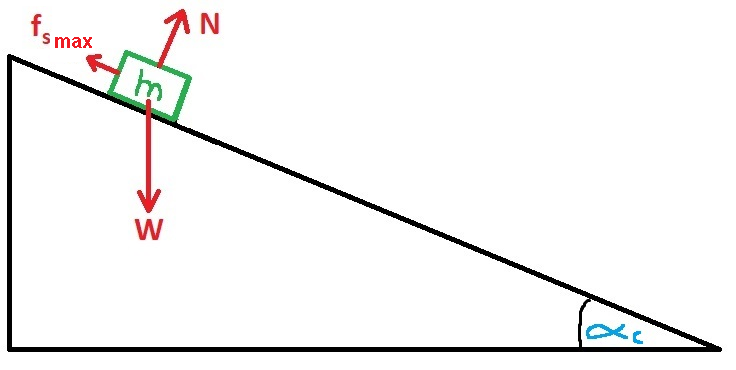
نحدد المحور X في اتجاه نحو منحدر السطح والمحور Y في اتجاه عمودي على المستوى.

نحلل قوة الجاذبية W إلى مركّبيها :

زاوية ميل المستوى هي الزاوية بين قوة الجاذبية W ومركب قوة الجاذبيةW_X.

في الاتجاه العمودي، يكون الجسم في وضع اتّزان، نكتب معادلات الحركة في الاتجاه العمودي، اتجاه المحور Y : 

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»W«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»§#945;«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

في اتجاه أسفل السطح، يكون الجسم أيضًا في وضع اتّزان، نكتب معادلات الحركة في اتجاه المحور X : 

         «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»max«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«/mstyle»«/math»

نعبر عن أقصى قوة احتكاك ساكن:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»W«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»§#945;«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/mstyle»«/math»

للتعبير عن الزاوية التي يكون فيها الجسم على عتبة الحركة ، نعوض تعبير القوة العمودية من معادلة الحركة في اتجاه المحور Y في معادلة الحركة في اتجاه المحور X. 

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#945;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/mstyle»«/math»

نقسم طرفي المعادلة بـ «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«/mstyle»«/math»:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»W«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»§#945;«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»W«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»§#945;«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»W«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»§#945;«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»W«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»§#945;«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»§#945;«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»§#945;«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/mstyle»«/math»

نعبر عن زاوية ميل السطح التي يكون فيها الجسم على عتبة الحركة: 

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨28px¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»§#945;«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»shift«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/mstyle»«/math»