حلول التدريبات العملية كينماتيكا - رسوم بيانية نوعية

6.ب- الرسم البياني V(t), ثلاث حركات مختلفة.

الرسم البياني المعطى هو رسم بياني للسرعة كدالة للزمن.

في الرسم البياني للسرعة كدالة للزمن، يكون ميل الدالة الموصوفة في الرسم البياني مساويًا لتسارع الجسم، والمساحة المحصورة بين الدالة ومحور الزمن تساوي ازاحة الحركة.

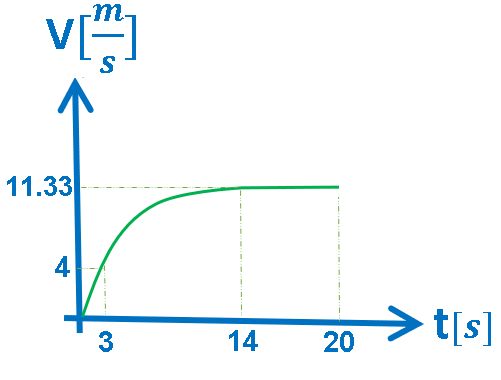
رياضياً: يمكن تقسيم الدوال الموصوفة في الرسم البياني إلى ثلاث دوال مختلفة:

الدالة الأولى: بالفترة الزمنية  «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#60;«/mo»«mn mathvariant=¨bold¨»3«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»: ميل الدالة موجب وثابت.  

الدالة الثانية: بالفترة الزمنية   «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»3«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#8804;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#8804;«/mo»«mn mathvariant=¨bold¨»14«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»: ميل الدالة آخذ بالنقصان حتى يصل إلى الصفر.

الدالة الثالثة: بالفترة الزمنية   «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»14«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#8804;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#8804;«/mo»«mn mathvariant=¨bold¨»20«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»: قيمة الدالة ثابتة.

نحسب تسارع الجسم في الجزء الأول من الحركة من ميل الدالة:

                                                                                                                   «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»v«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨ displaystyle=¨false¨»«mfrac»«mi»m«/mi»«msup»«mi»s«/mi»«mn»2«/mn»«/msup»«/mfrac»«/mstyle»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»33«/mn»«mstyle mathvariant=¨bold¨ displaystyle=¨false¨»«mfrac»«mi»m«/mi»«msup»«mi»s«/mi»«mn»2«/mn»«/msup»«/mfrac»«/mstyle»«/menclose»«/mstyle»«/math»

نحسب ازاحة الحركة في مقطع الحركة الأول من المساحة المحصورة في الثواني الثلاث الأولى: 

                                                          «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1587;§#1575;§#1581;§#1577;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»6«/mn»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mstyle»«/math»

نحسب ازاحة الحركة في مقطع الحركة الثالث من المساحة المحصورة في الثواني الست ثواني الأولى:

                                                                                                                                            «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1587;§#1575;§#1581;§#1577;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»11«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»67«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»98«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»98«/mn»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mstyle»«/math»

خلاصة: خلال ألـ 20 ثانية ، يتحرك الجسم في ثلاث حركات مختلفة.

في المرحلة الأولى ، يتحرك الجسم من حالة السكون بتسارع ثابت مقداره «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»33«/mn»«mfrac mathcolor=¨#FF6600¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/math» على طول ازاحة مقدارها 6 أمتار.

في المرحلة الثانية ، يتحرك الجسم بسرعة آخذة بالازدياد (مع تسارع آخذ بالنقصان) من سرعة 4 أمتار في الثانية إلى 11.33 مترًا في الثانية.

في المرحلة الثالثة ، يتحرك الجسم بسرعة ثابتة مقدارها 11.33 مترًا في الثانية لمدة 6 ثوانٍ على طول ازاحة مقدارها 67.98 مترًا.