حلول التدريبات العملية كينماتيكا - رسوم بيانية نوعية

4.أ- الرسم البياني V(t), حركة بتسارع ثابت.

الرسم البياني المعطى هو رسم بياني للسرعة كدالة للزمن.

في الرسم البياني للسرعة كدالة للزمن، يكون ميل الدالة الموصوفة في الرسم البياني مساويًا لتسارع الجسم، والمساحة المحصورة بين الدالة ومحور الزمن تساوي ازاحة الحركة.

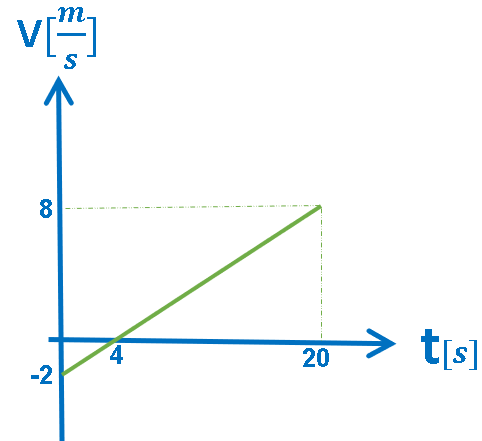
رياضياً: الرسم البياني يصف دالة خطية ذات ميل ثابت وموجب.

نحسب تسارع الجسم بواسطة حساب ميل الدالة الموصوفة في الرسم البياني:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»v«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»(«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»20«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨ displaystyle=¨false¨»«mfrac»«mi»m«/mi»«msup»«mi»s«/mi»«mn»2«/mn»«/msup»«/mfrac»«/mstyle»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mstyle displaystyle=¨false¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/menclose»«/mstyle»«/math»

نحسب ازاحة الجسم من المساحة المحصورة بين الدالة والمحور الزمني:

תחילה הגוף נע במהירות שלילית ולאחר מכן הוא משנה את כיוון תנועתו ונע במהירות חיובית.

في البداية، يتحرك الجسم بسرعة سالبة ثم يغير اتجاه حركته ويتحرك بسرعة موجبة.

نحسب ازاحة حركة الجسم خلال الثواني الأربع الأولى، في حركته عكس اتجاه المحور «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«/mstyle»«/math»:

نحسب ازاحة حركة الجسم في حركته باتجاه المحور «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«/mstyle»«/math»:

نحسب الإزاحة الكلية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«/mstyle»«/math»:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»64«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»60«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»X«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»60«/mn»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mstyle»«/math»

الخلاصة: بدأ الجسم يتحرك من سرعة ابتدائية مقدارها «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»2«/mn»«mfrac mathcolor=¨#FF6600¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math» , وهو يتحرك بتسارع ثابت مقداره «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF6600¨»45«/mn»«mfrac mathcolor=¨#FF6600¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math», لمدة 20 ثانية.

يتحرك الجسم في الثواني الأربع الأولى بسرعة سالبة ، ويتحرك عكس اتجاه المحور.

في اللحظة t = 4s ، يتوقف الجسم توقفًا لحظيًا ثم يغير اتجاه حركته ويتحرك في اتجاه المحور (بنفس التسارع) لمدة 16 ثانية أخرى.

ازاحة الجسم الكلية 60 مترا.