حل التدريبات العملية: الحركة التوافقية البسيطة في نابض أفقي وبندول بسيط

4.1

الصندوق موضوع على سطح أفقي أملس، وعند اصطدام الرصاصة، فإن حركة الصندوق والرصاصة تتأثر فقط بالقوى المتبادلة التي يؤثر بها كل منهما على الآخر (قوى داخلية) – لذلك تُحفظ كمية الحركة.

بعد اصطدام الرصاصة، تتحرك الأجسام معًا، وسنكتب معادلة حفظ كمية الحركة.

نرمز إلى الرصاصة بالجسم 1 وإلى الصندوق بالجسم 2.

سرعة الصندوق قبل الاصطدام تساوي صفرًا.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«/mstyle»«/math»

بعد اصطدام الرصاصة، يتحرك الصندوق والرصاصة معًا كجسم واحد، وسنتعامل مع اصطدام الرصاصة بالصندوق على أنه اصطدام لدن.

نرمز إلى سرعة الأجسام بعد الاصطدام بالرمز U.

نُعبّر عن سرعة الأجسام بعد الاصطدام على النحو التالي:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/mstyle»«/math»

بعد اصطدام الرصاصة، يكون قوة النابض هي القوة المحصلة التي تؤثر على الصندوق (وفي داخله الرصاصة)، لذلك يتحرك الصندوق في حركة توافقية بسيطة.

الصندوق لا يبدأ حركته من نقطة الطرف الموجبة، ولذلك لاستخدام دوال الحركة التوافقية البسيطة كدالة في الزمن، يجب استخدام زاوية الطور الابتدائية.

لتحديد قيمة زاوية الطور الابتدائية، يُوصَف في الرسم البياني التالي دالة موجة الجيب تمام باللون الأحمر، وحركة الجسم باللون الأزرق.

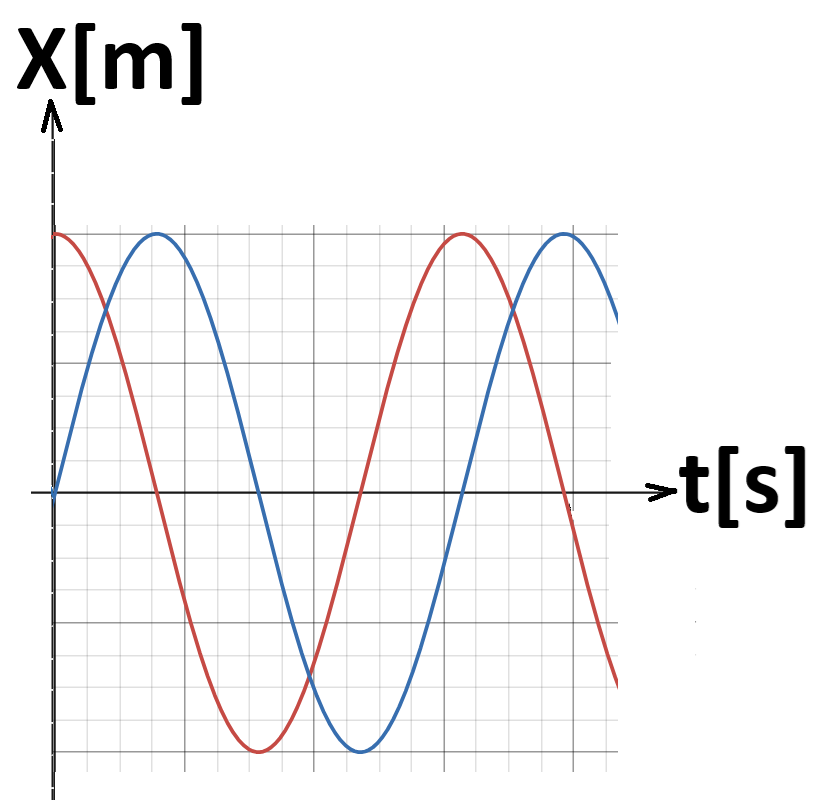
لكي تصف موجة الجيب تمام cos حركة الجسم، يجب إزاحة موجة cos إلى اليمين على محور الزمن بمقدار ربع دورة.

لذلك، فإن زاوية الطور الابتدائية هي: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«/math».

نكتب دالة السرعة كدالة في الزمن التي تصف حركة الجسم:

في لحظة بداية الحركة التوافقية البسيطة، يكون الصندوق (وبداخله الرصاصة) في نقطة أصل المحور، وسرعته هي السرعة $U$ U التي تم التعبير عنها من خلال حفظ كمية الحركة.

نكتب وفقًا لذلك دالة السرعة كدالة في الزمن، ونستخرج منها سعة الحركة.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»k«/mi»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»k«/mi»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»k«/mi»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»k«/mi»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»k«/mi»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«/msqrt»«/mstyle»«/math»

نُجري عمليات جبرية لتبسيط التعبير:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨18px¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨18px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathsize=¨18px¨»m«/mi»«mn mathvariant=¨bold¨ mathsize=¨18px¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨18px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨18px¨»V«/mi»«mn mathvariant=¨bold¨ mathsize=¨18px¨»1«/mn»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨ mathsize=¨18px¨»m«/mi»«mn mathvariant=¨bold¨ mathsize=¨18px¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨18px¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨18px¨»m«/mi»«mn mathvariant=¨bold¨ mathsize=¨18px¨»2«/mn»«/msub»«/mrow»«/mfrac»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨ mathsize=¨18px¨»m«/mi»«mn mathvariant=¨bold¨ mathsize=¨18px¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨18px¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨18px¨»m«/mi»«mn mathvariant=¨bold¨ mathsize=¨18px¨»2«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨ mathsize=¨18px¨»K«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨18px¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨18px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathsize=¨18px¨»m«/mi»«mn mathvariant=¨bold¨ mathsize=¨18px¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨18px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨18px¨»V«/mi»«mn mathvariant=¨bold¨ mathsize=¨18px¨»1«/mn»«/msub»«/mrow»«mrow»«menclose notation=¨updiagonalstrike¨»«msqrt»«msub»«mi mathvariant=¨bold¨ mathsize=¨18px¨»m«/mi»«mn mathvariant=¨bold¨ mathsize=¨18px¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨18px¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨18px¨»m«/mi»«mn mathvariant=¨bold¨ mathsize=¨18px¨»2«/mn»«/msub»«/msqrt»«/menclose»«mo mathvariant=¨bold¨ mathsize=¨18px¨»§#183;«/mo»«msqrt»«msub»«mi mathvariant=¨bold¨ mathsize=¨18px¨»m«/mi»«mn mathvariant=¨bold¨ mathsize=¨18px¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨18px¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨18px¨»m«/mi»«mn mathvariant=¨bold¨ mathsize=¨18px¨»2«/mn»«/msub»«/msqrt»«/mrow»«/mfrac»«mfrac mathcolor=¨#0000FF¨»«menclose notation=¨updiagonalstrike¨»«msqrt»«msub»«mi mathvariant=¨bold¨ mathsize=¨18px¨»m«/mi»«mn mathvariant=¨bold¨ mathsize=¨18px¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨18px¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨18px¨»m«/mi»«mn mathvariant=¨bold¨ mathsize=¨18px¨»2«/mn»«/msub»«/msqrt»«/menclose»«msqrt»«mi mathvariant=¨bold¨ mathsize=¨18px¨»K«/mi»«/msqrt»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨18px¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨18px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathsize=¨18px¨»m«/mi»«mn mathvariant=¨bold¨ mathsize=¨18px¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨18px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨18px¨»V«/mi»«mn mathvariant=¨bold¨ mathsize=¨18px¨»1«/mn»«/msub»«/mrow»«mrow»«msqrt»«msub»«mi mathvariant=¨bold¨ mathsize=¨18px¨»m«/mi»«mn mathvariant=¨bold¨ mathsize=¨18px¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨18px¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨18px¨»m«/mi»«mn mathvariant=¨bold¨ mathsize=¨18px¨»2«/mn»«/msub»«/msqrt»«mo mathvariant=¨bold¨ mathsize=¨18px¨»§#183;«/mo»«msqrt»«mi mathvariant=¨bold¨ mathsize=¨18px¨»K«/mi»«/msqrt»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨ mathsize=¨18px¨»A«/mi»«mo mathvariant=¨bold¨ mathsize=¨18px¨»=«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨ mathsize=¨18px¨»m«/mi»«mn mathvariant=¨bold¨ mathsize=¨18px¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨18px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨18px¨»V«/mi»«mn mathvariant=¨bold¨ mathsize=¨18px¨»1«/mn»«/msub»«/mrow»«msqrt»«mi mathvariant=¨bold¨ mathsize=¨18px¨»K«/mi»«mo mathvariant=¨bold¨ mathsize=¨18px¨»§#183;«/mo»«mstyle mathvariant=¨bold¨ mathsize=¨18px¨»«mo stretchy=¨true¨»(«/mo»«mrow»«msub»«mi»m«/mi»«mn»1«/mn»«/msub»«mo»+«/mo»«msub»«mi»m«/mi»«mn»2«/mn»«/msub»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«/msqrt»«/mfrac»«/menclose»«/math»